2021-2022学年人教版数学八年级 下册18.2.2 菱形(性质和判定)(第一课时)课件(共22张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学八年级 下册18.2.2 菱形(性质和判定)(第一课时)课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-19 15:24:32 | ||
图片预览


文档简介
(共22张PPT)
18.2.2 菱 形
第1课时 菱形的性质
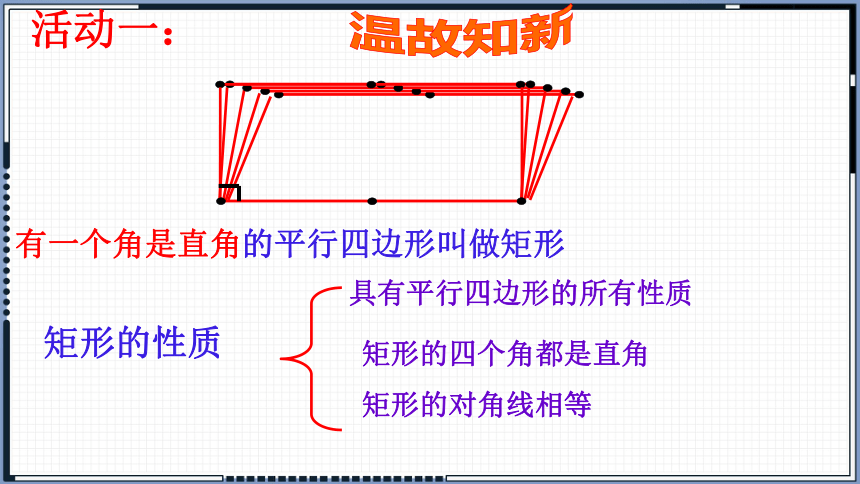
矩形的性质
矩形的四个角都是直角
矩形的对角线相等
有一个角是直角的平行四边形叫做矩形
活动一:
温故知新
具有平行四边形的所有性质
拼一拼
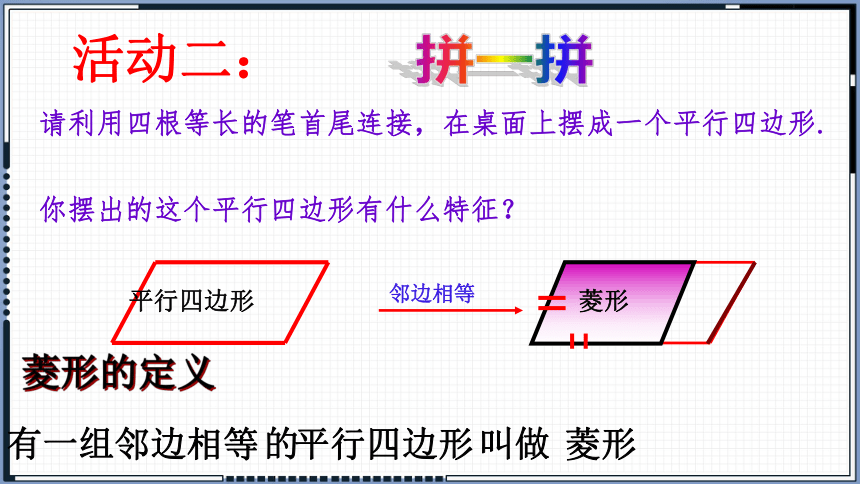
平行四边形
菱形
邻边相等
活动二:
请利用四根等长的笔首尾连接,在桌面上摆成一个平行四边形.
你摆出的这个平行四边形有什么特征?
菱形的定义
有一组 的 叫做
邻边相等
平行四边形
菱形
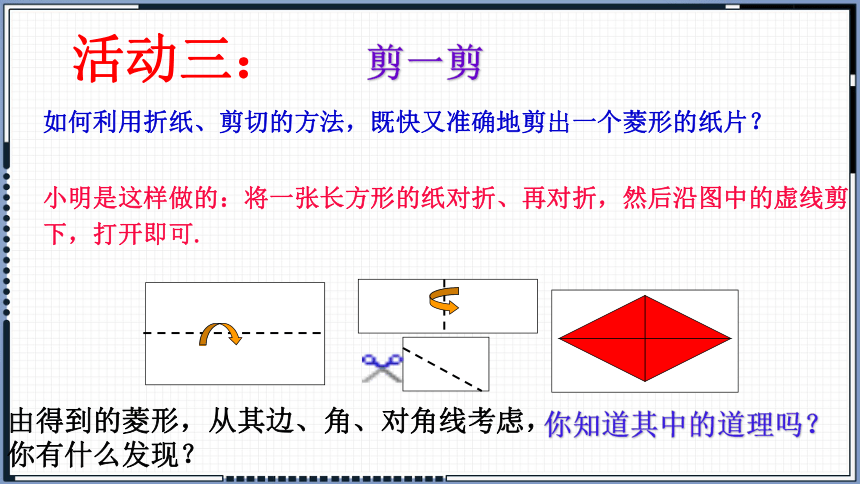
小明是这样做的:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可.
如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?
活动三:
剪一剪
你知道其中的道理吗?
由得到的菱形,从其边、角、对角线考虑,
你有什么发现?
A
B
C
D
O
菱形的性质
(1)菱形具有平行四边形的一切性质
(2)菱形的四条边相等
(3)菱形的两条对角线互相垂直,
并且每一条对角线平分一组对角。
A
B
C
D
O
B
O
D
C
A
O
D
B
A
C
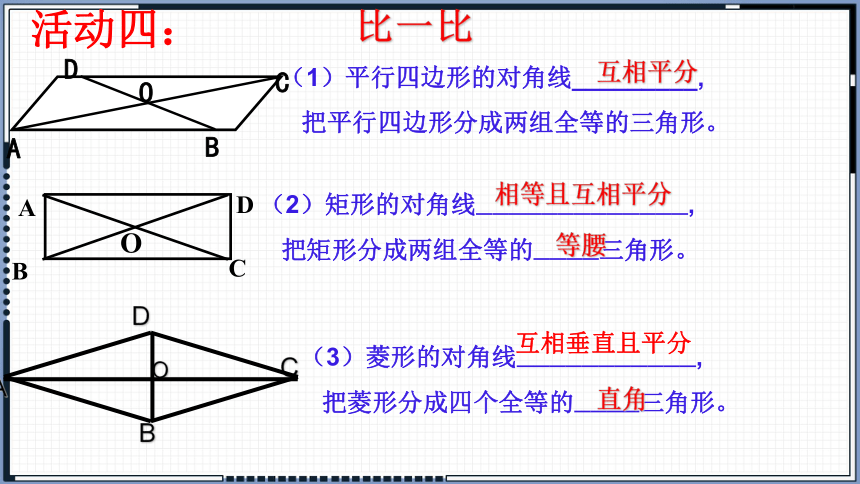
(1)平行四边形的对角线_________,
把平行四边形分成两组全等的三角形。
互相平分
(2)矩形的对角线—————————————,
把矩形分成两组全等的————三角形。
相等且互相平分
等腰
(3)菱形的对角线———————————,
把菱形分成四个全等的————三角形。
互相垂直且平分
直角
活动四:
比一比
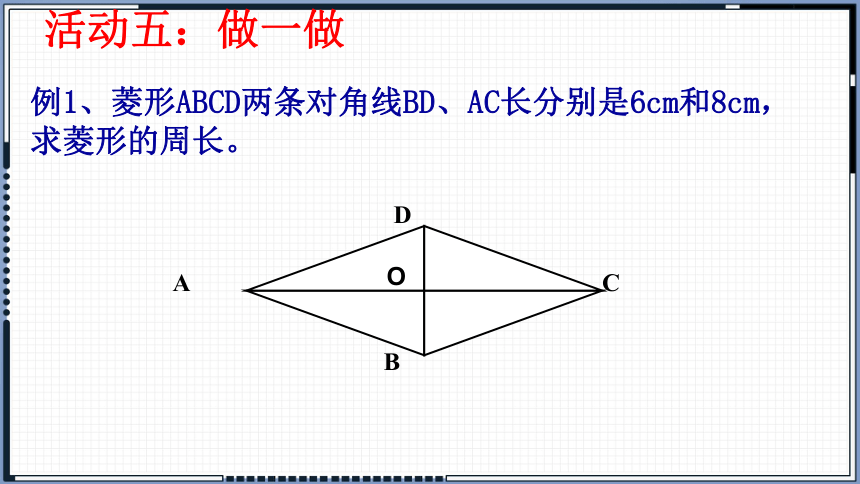
例1、菱形ABCD两条对角线BD、AC长分别是6cm和8cm,求菱形的周长。
C
B
D
A
O
活动五:做一做
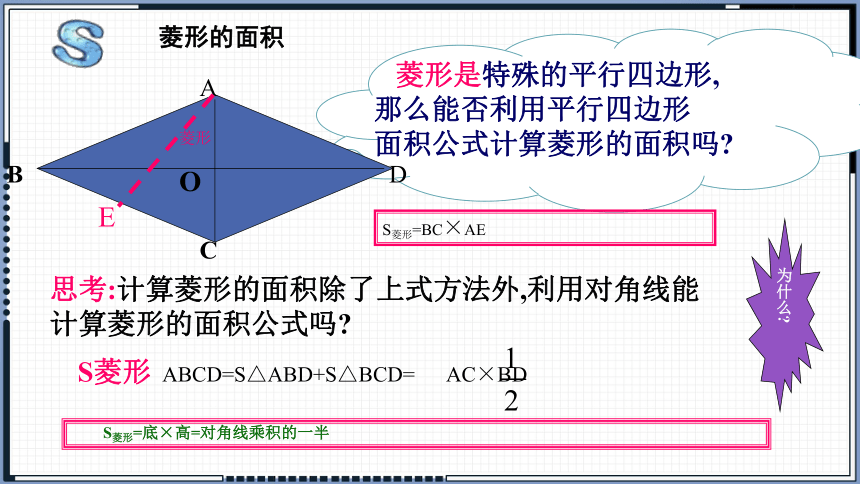
菱形是特殊的平行四边形,
那么能否利用平行四边形
面积公式计算菱形的面积吗
菱形
A
B
C
D
O
E
S菱形=BC×AE
思考:计算菱形的面积除了上式方法外,利用对角线能 计算菱形的面积公式吗
S菱形=底×高=对角线乘积的一半
为什么
菱形的面积
ABCD=S△ABD+S△BCD= AC×BD
S菱形
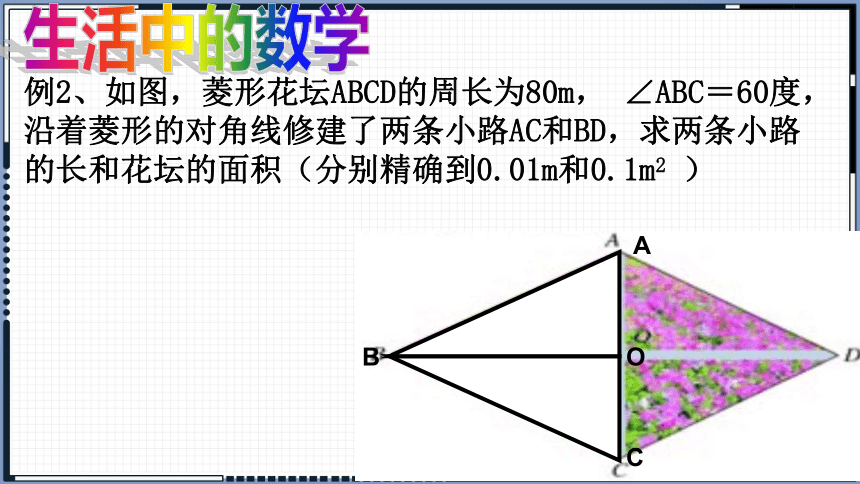
例2、如图,菱形花坛ABCD的周长为80m, ∠ABC=60度,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积(分别精确到0.01m和0.1m2 )
生活中的数学
B
A
O
C
巩固练习
1、已知菱形的两条对角线的长分别是6和8,求菱形的周长和面积。
2、四边形ABCD是菱形,对角线AC、BD相交
于点O,且AB=5,AO=4,求AC和BD的长。
这
堂
课
你
学
到
了
什
么?
回味无穷
从定义上来谈——
有一组邻边相等的平行四边形是 菱形.
从性质上来谈——
①菱形具有平行四边形的一切性质;
②菱形的四边都相等;
③菱形的对角线互相垂直平分,并且每条对角线平分一组对角。
从计算上来谈——
菱形的面积等于它的对角线长的乘积的一半。设菱形的两对角线长分别为a,b,则它的面积S=
ab.
18.2.2菱形
第2课时
推理验证出菱形的判定,并灵活应用。
导入
①边:四条边都相等
②对角线:互相垂直
学习了菱形的性质之后,又该如何判定得到菱形呢?
定义:有一组邻边相等的平行四边形是菱形
对比平行四边形,多了哪些性质呢?
已知:如图,在□ABCD中,AC BD,
求证:□ABCD是 _ .
⊥
证明:∵四边形ABCD是平行四边形,
∴A0= ,
又∵AC⊥BD,
∴AB=BC,(线段垂直平分线上的点
____ __ _)
∴□ABCD是菱形.
菱形
OC
到线段两端点的距离相等
难点突破 (菱形的判定定理)
(有一组 的 是菱形)
邻边相等
平行四边形
∵在 ABCD中,AC⊥BD
∴ ABCD是菱形
(有一组 的 是菱形)
证明:∵AB=DC,AD=BC,
∴四边形ABCD是_ _____ 形,
(两组对边分别____的四边形是平行四边形)
又∵AB=AD,
∴四边形ABCD是菱形.
已知:如图,在四边形ABCD中,
AB=___ =_ __=____.
菱形
BC
CD
AD
求证:四边形ABCD是 __ .
平行四边
相等
邻边相等
平行四边形
A
B
D
C
难点突破 (菱形的判定定理)
∵ 在四边形ABCD中
AB=BC=CD=DA
∴四边形ABCD是菱形
基础巩固
1.如图, ABCD 的对角线AC,BD相交于点O,且AB=5,AC=8,BD=6.
求证: ABCD是菱形
A
B
C
D
O
证明:∵四边形ABCD是平行四边形,AC=8,BD=6
∴OA=OC=4, OB=OD=3
∵AB=5
∴OA2+OB2=AB2
∴⊿AOB是直角三角形, 且∠AOB=900
∴ AC ⊥ BD
∴ ABCD是菱形
勾股定理
的逆定理
2.如图,两张等宽的纸条交叉叠放在一起,重合部分构成的四边形ABCD是什么形?怎么证明?
证明:
四边形ABCD是菱形。
过D作DF⊥BC于F
过B作BE⊥CD于E,
∵AD∥BC,AB∥CD
∴四边形ABCD是平行四边形
E
F
∴BC=CD
∴□ABCD是菱形.
强化提升
对于平行四边形ABCD
可以用等面积法,得:
又∵AD∥BC,AB∥CD
∵AE=AF
∴BC=CD
∴四边形ABCD是平行四边形
∴□ABCD是菱形.
四边形
平行四边形
菱 形
五条判定
一组邻边相等
对角线互相垂直
四条边都相等
小结:
菱形的判定:
判定的应用:
①基础巩固②强化提升(一题多解)
对角线互相平分且垂直
感谢聆听,再见!
18.2.2 菱 形
第1课时 菱形的性质
矩形的性质
矩形的四个角都是直角
矩形的对角线相等
有一个角是直角的平行四边形叫做矩形
活动一:
温故知新
具有平行四边形的所有性质
拼一拼
平行四边形
菱形
邻边相等
活动二:
请利用四根等长的笔首尾连接,在桌面上摆成一个平行四边形.
你摆出的这个平行四边形有什么特征?
菱形的定义
有一组 的 叫做
邻边相等
平行四边形
菱形
小明是这样做的:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可.
如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?
活动三:
剪一剪
你知道其中的道理吗?
由得到的菱形,从其边、角、对角线考虑,
你有什么发现?
A
B
C
D
O
菱形的性质
(1)菱形具有平行四边形的一切性质
(2)菱形的四条边相等
(3)菱形的两条对角线互相垂直,
并且每一条对角线平分一组对角。
A
B
C
D
O
B
O
D
C
A
O
D
B
A
C
(1)平行四边形的对角线_________,
把平行四边形分成两组全等的三角形。
互相平分
(2)矩形的对角线—————————————,
把矩形分成两组全等的————三角形。
相等且互相平分
等腰
(3)菱形的对角线———————————,
把菱形分成四个全等的————三角形。
互相垂直且平分
直角
活动四:
比一比
例1、菱形ABCD两条对角线BD、AC长分别是6cm和8cm,求菱形的周长。
C
B
D
A
O
活动五:做一做
菱形是特殊的平行四边形,
那么能否利用平行四边形
面积公式计算菱形的面积吗
菱形
A
B
C
D
O
E
S菱形=BC×AE
思考:计算菱形的面积除了上式方法外,利用对角线能 计算菱形的面积公式吗
S菱形=底×高=对角线乘积的一半
为什么
菱形的面积
ABCD=S△ABD+S△BCD= AC×BD
S菱形
例2、如图,菱形花坛ABCD的周长为80m, ∠ABC=60度,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积(分别精确到0.01m和0.1m2 )
生活中的数学
B
A
O
C
巩固练习
1、已知菱形的两条对角线的长分别是6和8,求菱形的周长和面积。
2、四边形ABCD是菱形,对角线AC、BD相交
于点O,且AB=5,AO=4,求AC和BD的长。
这
堂
课
你
学
到
了
什
么?
回味无穷
从定义上来谈——
有一组邻边相等的平行四边形是 菱形.
从性质上来谈——
①菱形具有平行四边形的一切性质;
②菱形的四边都相等;
③菱形的对角线互相垂直平分,并且每条对角线平分一组对角。
从计算上来谈——
菱形的面积等于它的对角线长的乘积的一半。设菱形的两对角线长分别为a,b,则它的面积S=
ab.
18.2.2菱形
第2课时
推理验证出菱形的判定,并灵活应用。
导入
①边:四条边都相等
②对角线:互相垂直
学习了菱形的性质之后,又该如何判定得到菱形呢?
定义:有一组邻边相等的平行四边形是菱形
对比平行四边形,多了哪些性质呢?
已知:如图,在□ABCD中,AC BD,
求证:□ABCD是 _ .
⊥
证明:∵四边形ABCD是平行四边形,
∴A0= ,
又∵AC⊥BD,
∴AB=BC,(线段垂直平分线上的点
____ __ _)
∴□ABCD是菱形.
菱形
OC
到线段两端点的距离相等
难点突破 (菱形的判定定理)
(有一组 的 是菱形)
邻边相等
平行四边形
∵在 ABCD中,AC⊥BD
∴ ABCD是菱形
(有一组 的 是菱形)
证明:∵AB=DC,AD=BC,
∴四边形ABCD是_ _____ 形,
(两组对边分别____的四边形是平行四边形)
又∵AB=AD,
∴四边形ABCD是菱形.
已知:如图,在四边形ABCD中,
AB=___ =_ __=____.
菱形
BC
CD
AD
求证:四边形ABCD是 __ .
平行四边
相等
邻边相等
平行四边形
A
B
D
C
难点突破 (菱形的判定定理)
∵ 在四边形ABCD中
AB=BC=CD=DA
∴四边形ABCD是菱形
基础巩固
1.如图, ABCD 的对角线AC,BD相交于点O,且AB=5,AC=8,BD=6.
求证: ABCD是菱形
A
B
C
D
O
证明:∵四边形ABCD是平行四边形,AC=8,BD=6
∴OA=OC=4, OB=OD=3
∵AB=5
∴OA2+OB2=AB2
∴⊿AOB是直角三角形, 且∠AOB=900
∴ AC ⊥ BD
∴ ABCD是菱形
勾股定理
的逆定理
2.如图,两张等宽的纸条交叉叠放在一起,重合部分构成的四边形ABCD是什么形?怎么证明?
证明:
四边形ABCD是菱形。
过D作DF⊥BC于F
过B作BE⊥CD于E,
∵AD∥BC,AB∥CD
∴四边形ABCD是平行四边形
E
F
∴BC=CD
∴□ABCD是菱形.
强化提升
对于平行四边形ABCD
可以用等面积法,得:
又∵AD∥BC,AB∥CD
∵AE=AF
∴BC=CD
∴四边形ABCD是平行四边形
∴□ABCD是菱形.
四边形
平行四边形
菱 形
五条判定
一组邻边相等
对角线互相垂直
四条边都相等
小结:
菱形的判定:
判定的应用:
①基础巩固②强化提升(一题多解)
对角线互相平分且垂直
感谢聆听,再见!
