2021-2022学年人教版九年级数学下册27.3 位似 练习题(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册27.3 位似 练习题(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 417.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-19 14:03:57 | ||
图片预览

文档简介
人教版九年级数学下册 第二十七章 相似 27.3 位似 练习题
一、选择题
1.如图,点在射线上,点在射线上,且,.若,的面积分别为1,4,则图中三个阴影三角形面积之和为 ( )
A.8 B.9 C.10 D.10.5
2.如图,图形甲与图形乙是位似图形,O是位似中心,位似比为2:3,点A,B的对应点分别为点A′,B′.若AB=6,则A′B′的长为( )
A.8 B.9 C.10 D.15
3.如图,已知线段AB的两个端点的坐标分别是A(m,m),B(2n,n),以原点O为位似中心,相似比为,把线段AB缩小,则经过位似变换后,A的对应点A′坐标是( )
A.(m,n) B.(m,m) C.( m, m) D.(n,n)
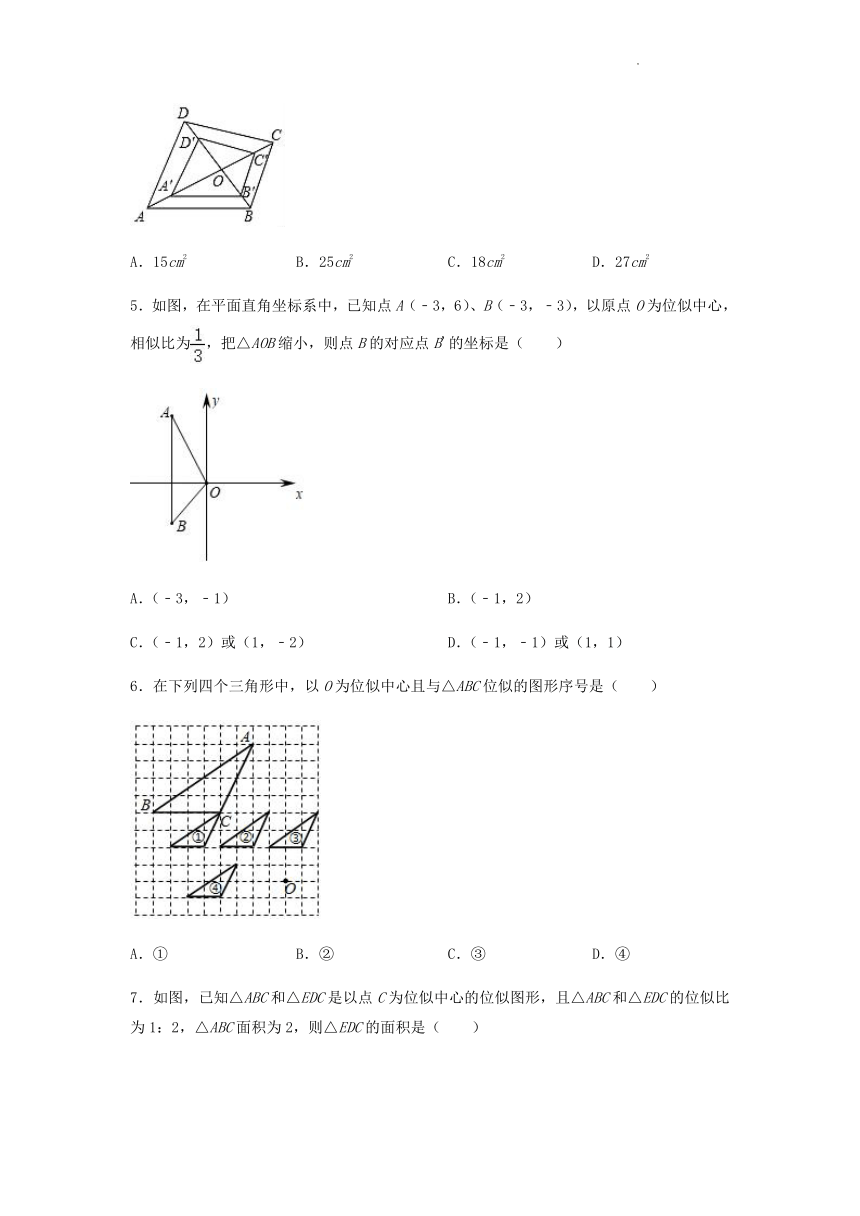
4.如图,四边形ABCD和A′B′C′D′是以点O为位似中心的位似图形,若OA′:OA=3:5,四边形A′B′C′D′的面积为9cm2,则四边形ABCD的面积为( )
A.15cm2 B.25cm2 C.18cm2 D.27cm2
5.如图,在平面直角坐标系中,已知点A(﹣3,6)、B(﹣3,﹣3),以原点O为位似中心,相似比为,把△AOB缩小,则点B的对应点B'的坐标是( )
A.(﹣3,﹣1) B.(﹣1,2)
C.(﹣1,2)或(1,﹣2) D.(﹣1,﹣1)或(1,1)
6.在下列四个三角形中,以O为位似中心且与△ABC位似的图形序号是( )
A.① B.② C.③ D.④
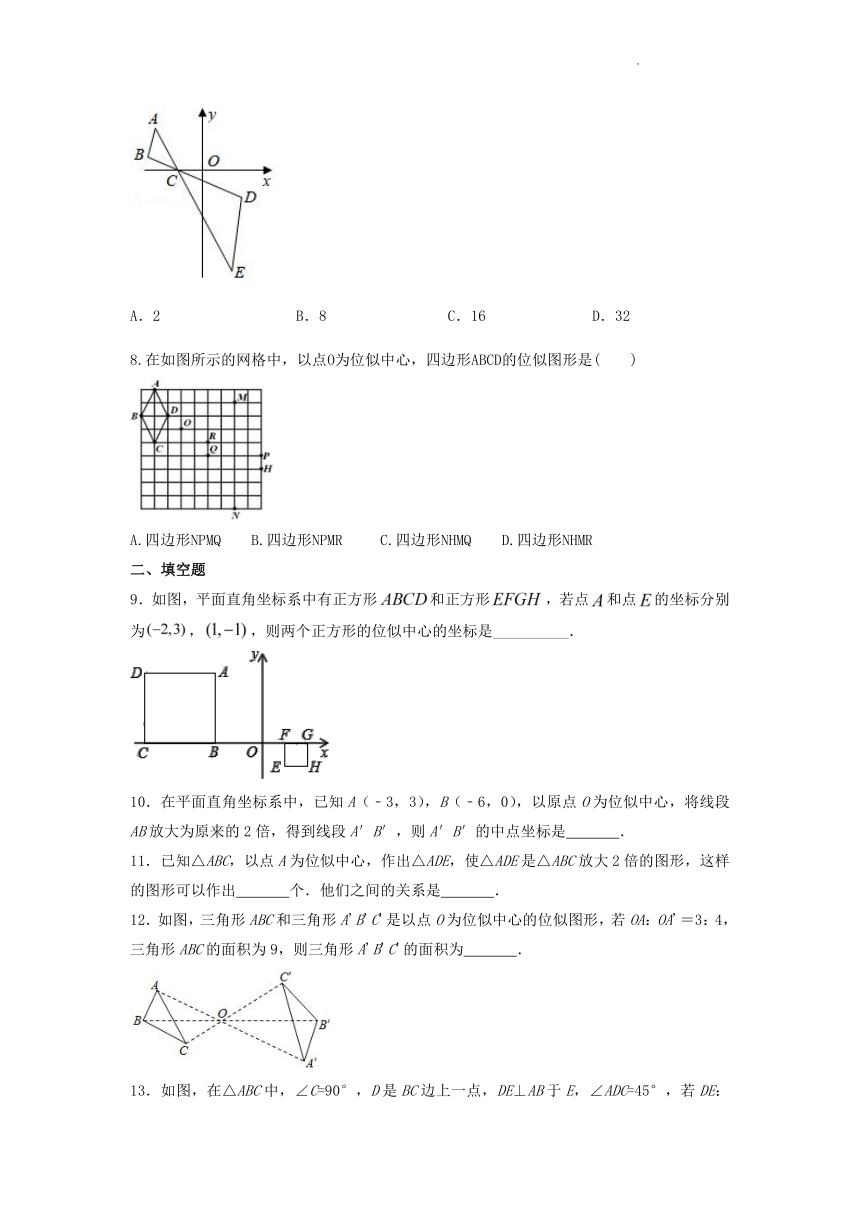
7.如图,已知△ABC和△EDC是以点C为位似中心的位似图形,且△ABC和△EDC的位似比为1:2,△ABC面积为2,则△EDC的面积是( )
A.2 B.8 C.16 D.32
8.在如图所示的网格中,以点O为位似中心,四边形ABCD的位似图形是( )
A.四边形NPMQ B.四边形NPMR C.四边形NHMQ D.四边形NHMR
二、填空题
9.如图,平面直角坐标系中有正方形和正方形,若点和点的坐标分别为,,则两个正方形的位似中心的坐标是__________.
10.在平面直角坐标系中,已知A(﹣3,3),B(﹣6,0),以原点O为位似中心,将线段AB放大为原来的2倍,得到线段A′B′,则A′B′的中点坐标是 .
11.已知△ABC,以点A为位似中心,作出△ADE,使△ADE是△ABC放大2倍的图形,这样的图形可以作出 个.他们之间的关系是 .
12.如图,三角形ABC和三角形A'B'C'是以点O为位似中心的位似图形,若OA:OA'=3:4,三角形ABC的面积为9,则三角形A'B'C'的面积为 .
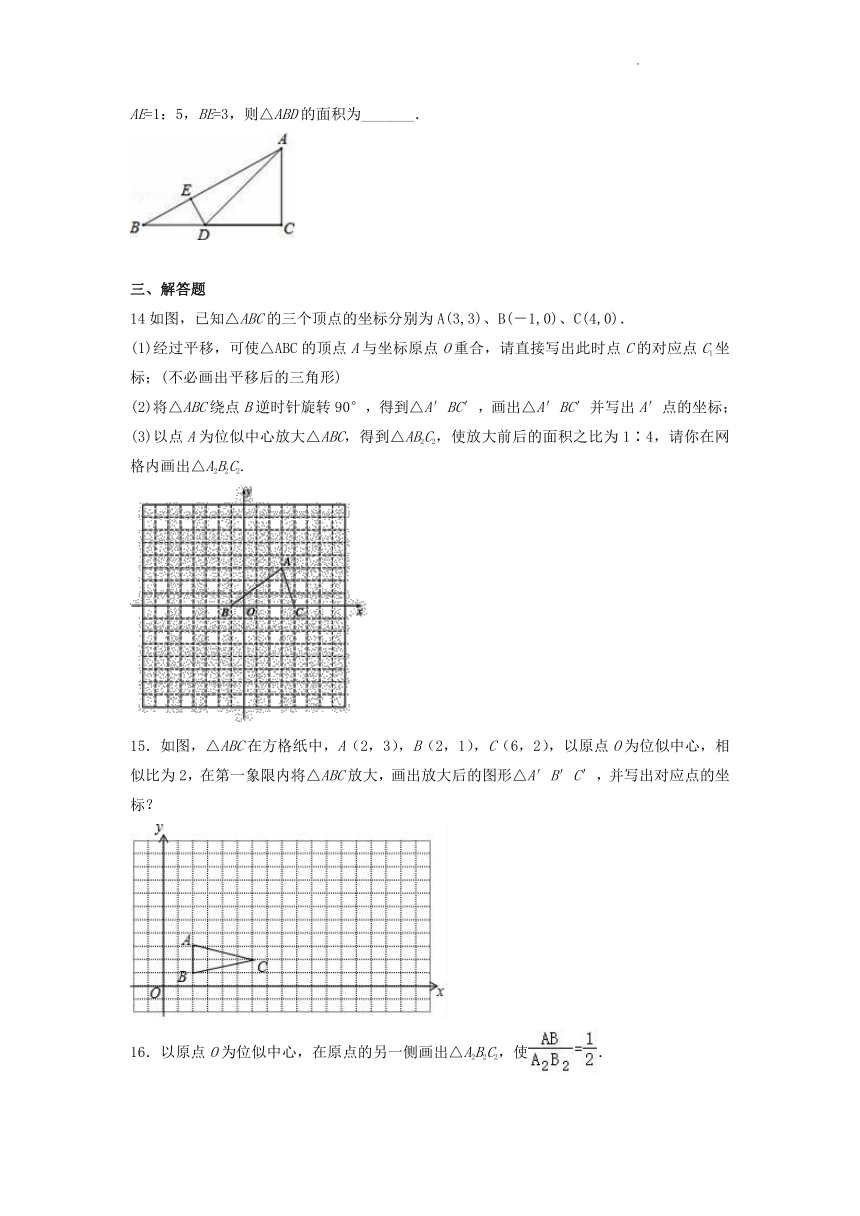
13.如图,在△ABC中,∠C=90°,D是BC边上一点,DE⊥AB于E,∠ADC=45°,若DE:AE=1:5,BE=3,则△ABD的面积为_______.
三、解答题
14如图,已知△ABC的三个顶点的坐标分别为A(3,3)、B(-1,0)、C(4,0).
(1)经过平移,可使△ABC的顶点A与坐标原点O重合,请直接写出此时点C的对应点C1坐标;(不必画出平移后的三角形)
(2)将△ABC绕点B逆时针旋转90°,得到△A′BC′,画出△A′BC′并写出A′点的坐标;
(3)以点A为位似中心放大△ABC,得到△AB2C2,使放大前后的面积之比为1∶4,请你在网格内画出△A2B2C2.
15.如图,△ABC在方格纸中,A(2,3),B(2,1),C(6,2),以原点O为位似中心,相似比为2,在第一象限内将△ABC放大,画出放大后的图形△A′B′C′,并写出对应点的坐标?
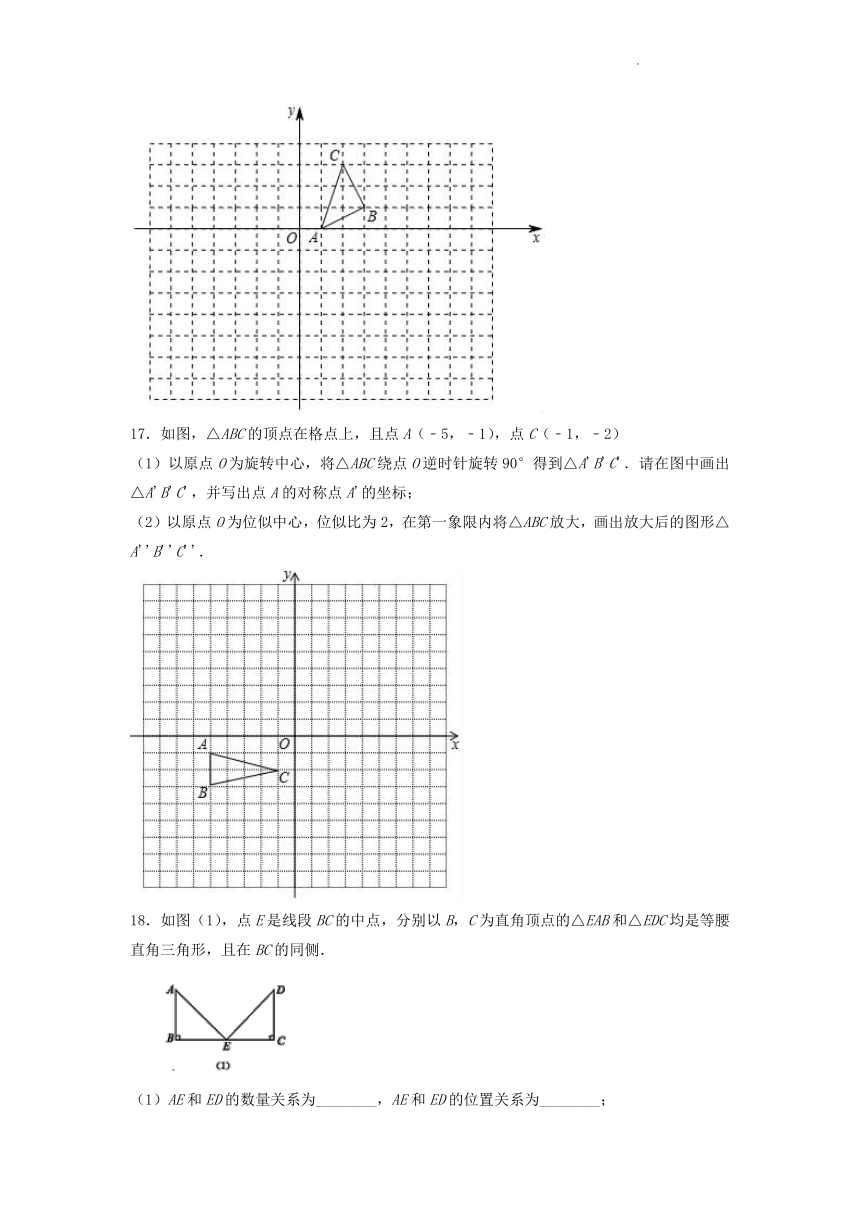
16.以原点O为位似中心,在原点的另一侧画出△A2B2C2,使.
17.如图,△ABC的顶点在格点上,且点A(﹣5,﹣1),点C(﹣1,﹣2)
(1)以原点O为旋转中心,将△ABC绕点O逆时针旋转90°得到△A'B'C'.请在图中画出△A'B'C',并写出点A的对称点A'的坐标;
(2)以原点O为位似中心,位似比为2,在第一象限内将△ABC放大,画出放大后的图形△A''B''C''.
18.如图(1),点E是线段BC的中点,分别以B,C为直角顶点的△EAB和△EDC均是等腰直角三角形,且在BC的同侧.
(1)AE和ED的数量关系为________,AE和ED的位置关系为________;
(2)在图(2)中,以点E为位似中心,作△EGF与△EAB位似,点H是BC所在直线上的一点,连接GH,HD,分别得到了图(2)和图(3).
①在图(2)中,点F在BE上,△EGF与△EAB的相似比是1∶2,H是EC的中点.
求证:GH=HD,GH⊥HD.
②在图(3)中,点F在BE的延长线上,△EGF与△EAB的相似比是k∶1,若BC=2,请直接写出CH的长为多少时,恰好使得GH=HD且GH⊥HD(用含k的代数式表示).
19.如图,在边长为1的正方形网格中,有一格点△ABC,已知A、B、C三点的坐标分别是A(1,0)、B(2,﹣1)、C(3,1).
(1)请在网格图形中画出平面直角坐标系;
(2)以原点O为位似中心,将△ABC放大2倍,在提供的网格中画出放大后的△A′B′C′;
(3)写出△A′B′C′各顶点的坐标:A′ ,B′ ,C′ ;
(4)求点A′到直线B'C'的距离.
20.如图,在由边长为1的小正方形组成的网格中,△ABC的三个顶点坐标分别为
A(﹣2,﹣2),B(﹣5,﹣4),C(﹣1,﹣5).
(1)请在网格中画出△ABC关于x轴对称的△A1B1C1.
(2)以点O为位似中心,将△ABC放大为原来的2倍,得到△A2B2C2,请在网格中画出△A2B2C2.
(3)①点B1的坐标为 ;
②求△A2B2C2的面积.
1.D
2.B
3.C
4.B
5.C
6.B
7.B
8.A
9. 或
10.(﹣9,3)或(9,﹣3).
11.2,成中心对称.
12.:16.
13.13
14.解:(1)∵经过平移,可使△ABC的顶点A与坐标原点O重合,
∴A点向下平移3个单位,再向左平移3个单位,故C1坐标为(1,-3);
(2)如图所示:△A′BC′即为所求,A′点的坐标为(-4,4);
(3)如图所示:△AB2C2,即为所求.
15.解:如图所示:△A′B′C′,即为所求;
A′(4,6),B′(4,2),C′(12,4).
16.解:(1)如图所示:△A1B1C1,即为所求,点A1的坐标为:(﹣3,2);
故答案为:(﹣3,2);
(2)如图所示:△A2B2C2,即为所求.
17解:(1)如图所示:△A'B'C',点A的对称点A'的坐标为:(1,﹣5);
(2)如图所示:△A''B''C''即为所求.
18.(1)∵点E是线段BC的中点,分别BC以为直角顶点的△EAB和△EDC均是等腰三角形,
∴BE=EC=DC=AB,∠B=∠C=90°,
∴△ABE≌△DCE,
∴AE=DE,
∠AEB=∠DEC=45°,
∴∠AED=90°,
∴AE⊥ED.
故答案为:AE=ED,AE⊥ED;
(2)①由题意,∠B=∠C=90°,AB=BE=EC=DC,
∵△EGF与△EAB的相似比1:2,
∴∠GFE=∠B=90°,GF=AB,EF=EB,
∴∠GFE=∠C,
∴EH=HC=EC,
∴GF=HC,FH=FE+EH=EB+EC=BC=EC=CD,
∴△HGF≌△DHC.
∴GH=HD,∠GHF=∠HDC.
∵∠HDC+∠DHC=90°.
∴∠GHF+∠DHC=90°
∴∠GHD=90°.
∴GH⊥HD.
②根据题意得出:∵当GH=HD,GH⊥HD时,
∴∠FHG+∠DHC=90°,
∵∠FHG+∠FGH=90°,
∴∠FGH=∠DHC,
∴,
∴△GFH≌△HCD,
∴CH=FG,
∵EF=FG,
∴EF=CH,
∵△EGF与△EAB的相似比是k:1,BC=2,
∴BE=EC=1,
∴EF=k,
∴CH的长为k.
19.解:(1)如图所示:平面直角坐标系即为所求;
(2)如图所示:△A′B′C′即为所求;
(3)A′(﹣2,0),B′(﹣4,2),C′(﹣6,﹣2);
故答案为:(﹣2,0),(﹣4,2),(﹣6,﹣2);
(4)设点A′到直线B'C'的距离为h,
则h×2=4×4﹣×2×4﹣×2×2﹣×2×4,
解得:h=.
20.解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作,C2 (﹣1,﹣2);
(3)①点B1的坐标为(﹣5,4);
②△A2B2C2的面积=4(4×3﹣×4×1﹣×3×1﹣×3×2)=22.
故答案为(﹣5,4).
一、选择题
1.如图,点在射线上,点在射线上,且,.若,的面积分别为1,4,则图中三个阴影三角形面积之和为 ( )
A.8 B.9 C.10 D.10.5
2.如图,图形甲与图形乙是位似图形,O是位似中心,位似比为2:3,点A,B的对应点分别为点A′,B′.若AB=6,则A′B′的长为( )
A.8 B.9 C.10 D.15
3.如图,已知线段AB的两个端点的坐标分别是A(m,m),B(2n,n),以原点O为位似中心,相似比为,把线段AB缩小,则经过位似变换后,A的对应点A′坐标是( )
A.(m,n) B.(m,m) C.( m, m) D.(n,n)
4.如图,四边形ABCD和A′B′C′D′是以点O为位似中心的位似图形,若OA′:OA=3:5,四边形A′B′C′D′的面积为9cm2,则四边形ABCD的面积为( )
A.15cm2 B.25cm2 C.18cm2 D.27cm2
5.如图,在平面直角坐标系中,已知点A(﹣3,6)、B(﹣3,﹣3),以原点O为位似中心,相似比为,把△AOB缩小,则点B的对应点B'的坐标是( )
A.(﹣3,﹣1) B.(﹣1,2)
C.(﹣1,2)或(1,﹣2) D.(﹣1,﹣1)或(1,1)
6.在下列四个三角形中,以O为位似中心且与△ABC位似的图形序号是( )
A.① B.② C.③ D.④
7.如图,已知△ABC和△EDC是以点C为位似中心的位似图形,且△ABC和△EDC的位似比为1:2,△ABC面积为2,则△EDC的面积是( )
A.2 B.8 C.16 D.32
8.在如图所示的网格中,以点O为位似中心,四边形ABCD的位似图形是( )
A.四边形NPMQ B.四边形NPMR C.四边形NHMQ D.四边形NHMR
二、填空题
9.如图,平面直角坐标系中有正方形和正方形,若点和点的坐标分别为,,则两个正方形的位似中心的坐标是__________.
10.在平面直角坐标系中,已知A(﹣3,3),B(﹣6,0),以原点O为位似中心,将线段AB放大为原来的2倍,得到线段A′B′,则A′B′的中点坐标是 .
11.已知△ABC,以点A为位似中心,作出△ADE,使△ADE是△ABC放大2倍的图形,这样的图形可以作出 个.他们之间的关系是 .
12.如图,三角形ABC和三角形A'B'C'是以点O为位似中心的位似图形,若OA:OA'=3:4,三角形ABC的面积为9,则三角形A'B'C'的面积为 .
13.如图,在△ABC中,∠C=90°,D是BC边上一点,DE⊥AB于E,∠ADC=45°,若DE:AE=1:5,BE=3,则△ABD的面积为_______.
三、解答题
14如图,已知△ABC的三个顶点的坐标分别为A(3,3)、B(-1,0)、C(4,0).
(1)经过平移,可使△ABC的顶点A与坐标原点O重合,请直接写出此时点C的对应点C1坐标;(不必画出平移后的三角形)
(2)将△ABC绕点B逆时针旋转90°,得到△A′BC′,画出△A′BC′并写出A′点的坐标;
(3)以点A为位似中心放大△ABC,得到△AB2C2,使放大前后的面积之比为1∶4,请你在网格内画出△A2B2C2.
15.如图,△ABC在方格纸中,A(2,3),B(2,1),C(6,2),以原点O为位似中心,相似比为2,在第一象限内将△ABC放大,画出放大后的图形△A′B′C′,并写出对应点的坐标?
16.以原点O为位似中心,在原点的另一侧画出△A2B2C2,使.
17.如图,△ABC的顶点在格点上,且点A(﹣5,﹣1),点C(﹣1,﹣2)
(1)以原点O为旋转中心,将△ABC绕点O逆时针旋转90°得到△A'B'C'.请在图中画出△A'B'C',并写出点A的对称点A'的坐标;
(2)以原点O为位似中心,位似比为2,在第一象限内将△ABC放大,画出放大后的图形△A''B''C''.
18.如图(1),点E是线段BC的中点,分别以B,C为直角顶点的△EAB和△EDC均是等腰直角三角形,且在BC的同侧.
(1)AE和ED的数量关系为________,AE和ED的位置关系为________;
(2)在图(2)中,以点E为位似中心,作△EGF与△EAB位似,点H是BC所在直线上的一点,连接GH,HD,分别得到了图(2)和图(3).
①在图(2)中,点F在BE上,△EGF与△EAB的相似比是1∶2,H是EC的中点.
求证:GH=HD,GH⊥HD.
②在图(3)中,点F在BE的延长线上,△EGF与△EAB的相似比是k∶1,若BC=2,请直接写出CH的长为多少时,恰好使得GH=HD且GH⊥HD(用含k的代数式表示).
19.如图,在边长为1的正方形网格中,有一格点△ABC,已知A、B、C三点的坐标分别是A(1,0)、B(2,﹣1)、C(3,1).
(1)请在网格图形中画出平面直角坐标系;
(2)以原点O为位似中心,将△ABC放大2倍,在提供的网格中画出放大后的△A′B′C′;
(3)写出△A′B′C′各顶点的坐标:A′ ,B′ ,C′ ;
(4)求点A′到直线B'C'的距离.
20.如图,在由边长为1的小正方形组成的网格中,△ABC的三个顶点坐标分别为
A(﹣2,﹣2),B(﹣5,﹣4),C(﹣1,﹣5).
(1)请在网格中画出△ABC关于x轴对称的△A1B1C1.
(2)以点O为位似中心,将△ABC放大为原来的2倍,得到△A2B2C2,请在网格中画出△A2B2C2.
(3)①点B1的坐标为 ;
②求△A2B2C2的面积.
1.D
2.B
3.C
4.B
5.C
6.B
7.B
8.A
9. 或
10.(﹣9,3)或(9,﹣3).
11.2,成中心对称.
12.:16.
13.13
14.解:(1)∵经过平移,可使△ABC的顶点A与坐标原点O重合,
∴A点向下平移3个单位,再向左平移3个单位,故C1坐标为(1,-3);
(2)如图所示:△A′BC′即为所求,A′点的坐标为(-4,4);
(3)如图所示:△AB2C2,即为所求.
15.解:如图所示:△A′B′C′,即为所求;
A′(4,6),B′(4,2),C′(12,4).
16.解:(1)如图所示:△A1B1C1,即为所求,点A1的坐标为:(﹣3,2);
故答案为:(﹣3,2);
(2)如图所示:△A2B2C2,即为所求.
17解:(1)如图所示:△A'B'C',点A的对称点A'的坐标为:(1,﹣5);
(2)如图所示:△A''B''C''即为所求.
18.(1)∵点E是线段BC的中点,分别BC以为直角顶点的△EAB和△EDC均是等腰三角形,
∴BE=EC=DC=AB,∠B=∠C=90°,
∴△ABE≌△DCE,
∴AE=DE,
∠AEB=∠DEC=45°,
∴∠AED=90°,
∴AE⊥ED.
故答案为:AE=ED,AE⊥ED;
(2)①由题意,∠B=∠C=90°,AB=BE=EC=DC,
∵△EGF与△EAB的相似比1:2,
∴∠GFE=∠B=90°,GF=AB,EF=EB,
∴∠GFE=∠C,
∴EH=HC=EC,
∴GF=HC,FH=FE+EH=EB+EC=BC=EC=CD,
∴△HGF≌△DHC.
∴GH=HD,∠GHF=∠HDC.
∵∠HDC+∠DHC=90°.
∴∠GHF+∠DHC=90°
∴∠GHD=90°.
∴GH⊥HD.
②根据题意得出:∵当GH=HD,GH⊥HD时,
∴∠FHG+∠DHC=90°,
∵∠FHG+∠FGH=90°,
∴∠FGH=∠DHC,
∴,
∴△GFH≌△HCD,
∴CH=FG,
∵EF=FG,
∴EF=CH,
∵△EGF与△EAB的相似比是k:1,BC=2,
∴BE=EC=1,
∴EF=k,
∴CH的长为k.
19.解:(1)如图所示:平面直角坐标系即为所求;
(2)如图所示:△A′B′C′即为所求;
(3)A′(﹣2,0),B′(﹣4,2),C′(﹣6,﹣2);
故答案为:(﹣2,0),(﹣4,2),(﹣6,﹣2);
(4)设点A′到直线B'C'的距离为h,
则h×2=4×4﹣×2×4﹣×2×2﹣×2×4,
解得:h=.
20.解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作,C2 (﹣1,﹣2);
(3)①点B1的坐标为(﹣5,4);
②△A2B2C2的面积=4(4×3﹣×4×1﹣×3×1﹣×3×2)=22.
故答案为(﹣5,4).
