2021-2022学年人教版八年级数学下册18.1.1平行四边形的性质练习题(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册18.1.1平行四边形的性质练习题(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 447.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-19 14:05:59 | ||
图片预览


文档简介
18.1.1 平行四边形的性质 练习题
一、选择题
1.下列性质中,平行四边形不具有的是( )
A.对角线相等 B.对角线互相平分
C.相邻两角互补 D.两组对边分别相等
2.在平行四边形ABCD中,∠A比∠B大40°,那么∠D的度数为( )
A.60° B.70° C.80° D.110°
3.如图,在中,已知,,,过的中点作,垂足为点,与的延长线相交于点,则的面积是( )
A. B. C. D.
4.如图,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF,CF,则下列结论:①∠DCF=∠BCD;②∠DFC+∠ECF=90o;③S△CEF>S△CDF;④∠EFC=∠BCF+∠AEF,其中正确结论的个数是( )
A.1个 B.2个
C.3个 D.4个
5.如图,在 ABCD中,对角线AC、BD相交于点O,过点O作OE⊥AC,交AD于点E,连接CE,若△CDE的周长为8,则 ABCD的周长为( )
A.8 B.10 C.16 D.20
6.如图,的对角线交于点O,E是CD的中点,若,则的值为( )
A.2 B.4 C.8 D.16
7.如图,的对角线、相交于点,则下列结论一定成立的是( )
A. B.
C. D.
8.如图,在中,,是的中点,作,垂足在线段上,连接,,则下列结论:①;②;③;④.其中结论正确的序号是( )
A.①② B.②③④ C.①②④ D.①②③④
9.如图,在 ABCD中,AB>AD,小于AD的长为半径画弧,分别交AB,F;再分别以点E,F为圆心EF的长为半径画弧,两弧交于点G,则下列结论中错误的是( )
A.AG平分∠DAB B.AD=DH C.DH=BC D.CH=DH
10.如图,将放置在平面直角坐标系中,点,当直线平分的面积时,则的值为( )
A. B. C. D.
二、填空题
11.在□ABCD中,AC与BD相交于点O,∠AOB=60°,BD=4,将△ABC沿直线AC翻折后,点B落在点B′处,那么DB′的长为_________
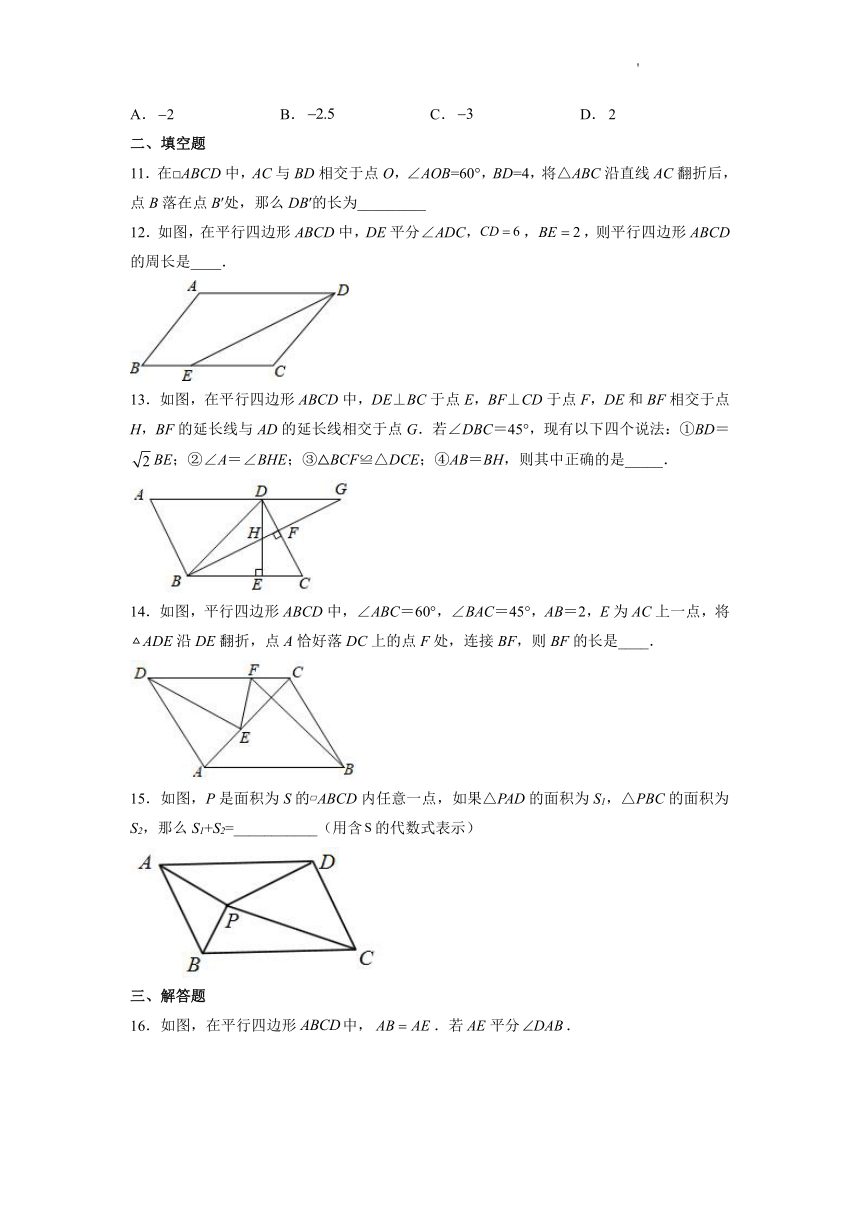
12.如图,在平行四边形ABCD中,DE平分∠ADC,,,则平行四边形ABCD的周长是____.
13.如图,在平行四边形ABCD中,DE⊥BC于点E,BF⊥CD于点F,DE和BF相交于点H,BF的延长线与AD的延长线相交于点G.若∠DBC=45°,现有以下四个说法:①BD=BE;②∠A=∠BHE;③△BCF≌△DCE;④AB=BH,则其中正确的是_____.
14.如图,平行四边形ABCD中,∠ABC=60°,∠BAC=45°,AB=2,E为AC上一点,将ADE沿DE翻折,点A恰好落DC上的点F处,连接BF,则BF的长是____.
15.如图,P是面积为S的 ABCD内任意一点,如果△PAD的面积为S1,△PBC的面积为S2,那么S1+S2=___________(用含的代数式表示)
三、解答题
16.如图,在平行四边形中,.若平分.
(1)求证:≌;
(2)若,求:的度数.
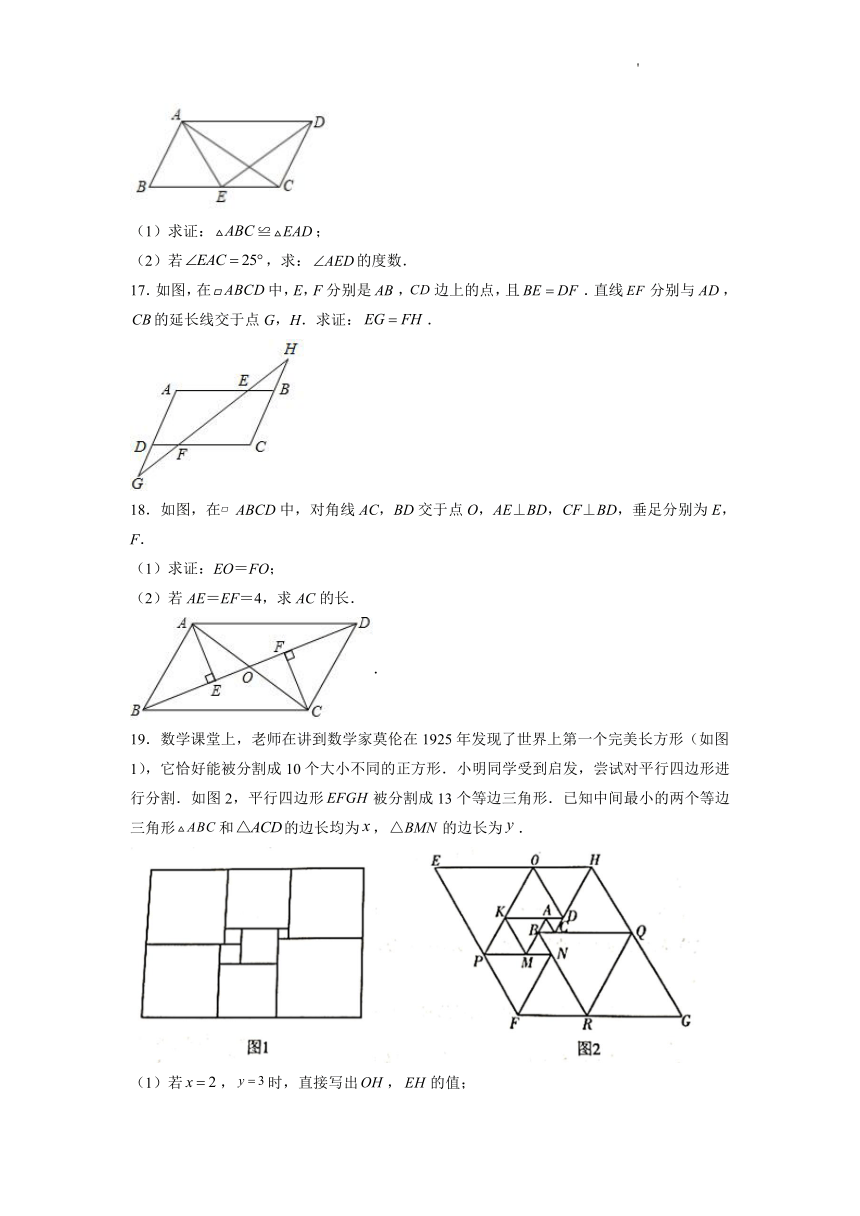
17.如图,在中,E,F分别是,边上的点,且.直线分别与,的延长线交于点G,H.求证:.
18.如图,在 ABCD中,对角线AC,BD交于点O,AE⊥BD,CF⊥BD,垂足分别为E,F.
(1)求证:EO=FO;
(2)若AE=EF=4,求AC的长.
.
19.数学课堂上,老师在讲到数学家莫伦在1925年发现了世界上第一个完美长方形(如图1),它恰好能被分割成10个大小不同的正方形.小明同学受到启发,尝试对平行四边形进行分割.如图2,平行四边形被分割成13个等边三角形.已知中间最小的两个等边三角形和的边长均为,的边长为.
(1)若,时,直接写出,的值;
(2)求的值.
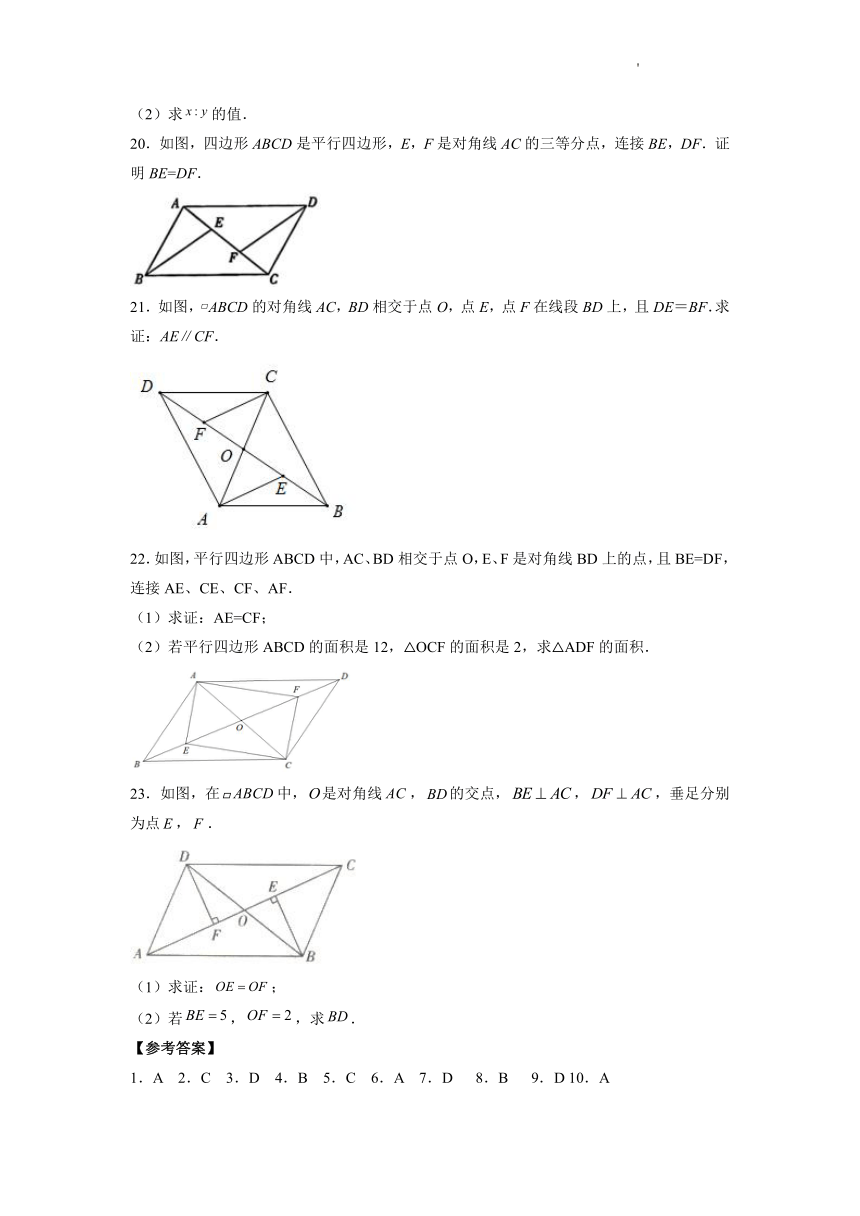
20.如图,四边形ABCD是平行四边形,E,F是对角线AC的三等分点,连接BE,DF.证明BE=DF.
21.如图, ABCD的对角线AC,BD相交于点O,点E,点F在线段BD上,且DE=BF.求证:AE∥CF.
22.如图,平行四边形ABCD中,AC、BD相交于点O,E、F是对角线BD上的点,且BE=DF,连接AE、CE、CF、AF.
(1)求证:AE=CF;
(2)若平行四边形ABCD的面积是12,△OCF的面积是2,求△ADF的面积.
23.如图,在中,是对角线,的交点,,,垂足分别为点,.
(1)求证:;
(2)若,,求.
【参考答案】
1.A 2.C 3.D 4.B 5.C 6.A 7.D 8.B 9.D 10.A
11.2
12.28
13.①②④
14.2
15.
16.解:(1)证明:∵四边形为平行四边形,
∴,,
∴,
∵,
∴,
∴,
在和中,,
∴≌;
(2)∵平分,
∴,
又∵,
∴,
∴为等边三角形,
∴,
∵,
∴,
∵≌,
∴,
∴.
17.证明:四边形为平行四边形,
,
,
又,
,
在和中,
,
,
,
,
即.
18.(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABE=∠CDF,
∵AE⊥ED,CF⊥BD,
∴∠AEB=∠CFD=90°,
在△ABE和△CDF中,
,
∴,
∴BE=DF,
∵OB=OD,
∴OB-BE=OD-DF,
∴OE=OF.
(2)∵AE=EF=4,
∴OE=OF=,
∴在中,,
∴.
19.(1)依题意,图中13个三角形为等边三角形
△ABC边长为x,△BMN边长为y,
AM=x+y,AK=AM=x+y, DK=x+y+x=2x+y,
DK=DO=OH,
OH=2x+y,OK=2x+y,
PK=KM=AK=x+y,
EO=OK+KP=2x+y+x+y=3x+2y,
EH=EO+OH=3x+2y+2x+y=5x+3y,
当,时,
OH=7,;
(2)由(1)得:EH=5x+3y,
FR=PN=PM+MN=x+y+y=x+2y,
RG=RB=RN+BN=FR+BN=x+2y+y=x+3y,
FG=FR+RG=x+2y+x+3y=2x+5y,
四边形是平行四边形,
EH=FG,
5x+3y=2x+5y,
整理得:3x=2y,
即x:y=2:3.
20.证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠BAE=∠DCF,
∵E,F是对角线AC的三等分点,
∴AE=CF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS),
∴BE=DF.
21.证:∵四边形ABCD是平行四边形,
∴AD=CB,AD∥BC,
∴∠ADE=∠CBF,
在△ADE和△CBF中,
∴△ADE≌△CBF(SAS),
∴∠AED=∠CFB,
∴AE∥CF.
22.(1)∵四边形ABCD是平行四边形,
∴ ,
在和中,
;
(2)如图,过点A作AG⊥BD于点G,过点C作CH⊥BD于点H,
,
.
∵四边形ABCD是平行四边形,
∴ ,
在和中,
.
底相等,高也相等,所以面积也相等,
.
底相同,高相等,所以面积也相等,
.
23.解:(1)证明:四边形是平行四边形,
.
,,
.
在和中,
.
.
(2)由(1)得:,
,
.
,
.
在中,.
一、选择题
1.下列性质中,平行四边形不具有的是( )
A.对角线相等 B.对角线互相平分
C.相邻两角互补 D.两组对边分别相等
2.在平行四边形ABCD中,∠A比∠B大40°,那么∠D的度数为( )
A.60° B.70° C.80° D.110°
3.如图,在中,已知,,,过的中点作,垂足为点,与的延长线相交于点,则的面积是( )
A. B. C. D.
4.如图,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF,CF,则下列结论:①∠DCF=∠BCD;②∠DFC+∠ECF=90o;③S△CEF>S△CDF;④∠EFC=∠BCF+∠AEF,其中正确结论的个数是( )
A.1个 B.2个
C.3个 D.4个
5.如图,在 ABCD中,对角线AC、BD相交于点O,过点O作OE⊥AC,交AD于点E,连接CE,若△CDE的周长为8,则 ABCD的周长为( )
A.8 B.10 C.16 D.20
6.如图,的对角线交于点O,E是CD的中点,若,则的值为( )
A.2 B.4 C.8 D.16
7.如图,的对角线、相交于点,则下列结论一定成立的是( )
A. B.
C. D.
8.如图,在中,,是的中点,作,垂足在线段上,连接,,则下列结论:①;②;③;④.其中结论正确的序号是( )
A.①② B.②③④ C.①②④ D.①②③④
9.如图,在 ABCD中,AB>AD,小于AD的长为半径画弧,分别交AB,F;再分别以点E,F为圆心EF的长为半径画弧,两弧交于点G,则下列结论中错误的是( )
A.AG平分∠DAB B.AD=DH C.DH=BC D.CH=DH
10.如图,将放置在平面直角坐标系中,点,当直线平分的面积时,则的值为( )
A. B. C. D.
二、填空题
11.在□ABCD中,AC与BD相交于点O,∠AOB=60°,BD=4,将△ABC沿直线AC翻折后,点B落在点B′处,那么DB′的长为_________
12.如图,在平行四边形ABCD中,DE平分∠ADC,,,则平行四边形ABCD的周长是____.
13.如图,在平行四边形ABCD中,DE⊥BC于点E,BF⊥CD于点F,DE和BF相交于点H,BF的延长线与AD的延长线相交于点G.若∠DBC=45°,现有以下四个说法:①BD=BE;②∠A=∠BHE;③△BCF≌△DCE;④AB=BH,则其中正确的是_____.
14.如图,平行四边形ABCD中,∠ABC=60°,∠BAC=45°,AB=2,E为AC上一点,将ADE沿DE翻折,点A恰好落DC上的点F处,连接BF,则BF的长是____.
15.如图,P是面积为S的 ABCD内任意一点,如果△PAD的面积为S1,△PBC的面积为S2,那么S1+S2=___________(用含的代数式表示)
三、解答题
16.如图,在平行四边形中,.若平分.
(1)求证:≌;
(2)若,求:的度数.
17.如图,在中,E,F分别是,边上的点,且.直线分别与,的延长线交于点G,H.求证:.
18.如图,在 ABCD中,对角线AC,BD交于点O,AE⊥BD,CF⊥BD,垂足分别为E,F.
(1)求证:EO=FO;
(2)若AE=EF=4,求AC的长.
.
19.数学课堂上,老师在讲到数学家莫伦在1925年发现了世界上第一个完美长方形(如图1),它恰好能被分割成10个大小不同的正方形.小明同学受到启发,尝试对平行四边形进行分割.如图2,平行四边形被分割成13个等边三角形.已知中间最小的两个等边三角形和的边长均为,的边长为.
(1)若,时,直接写出,的值;
(2)求的值.
20.如图,四边形ABCD是平行四边形,E,F是对角线AC的三等分点,连接BE,DF.证明BE=DF.
21.如图, ABCD的对角线AC,BD相交于点O,点E,点F在线段BD上,且DE=BF.求证:AE∥CF.
22.如图,平行四边形ABCD中,AC、BD相交于点O,E、F是对角线BD上的点,且BE=DF,连接AE、CE、CF、AF.
(1)求证:AE=CF;
(2)若平行四边形ABCD的面积是12,△OCF的面积是2,求△ADF的面积.
23.如图,在中,是对角线,的交点,,,垂足分别为点,.
(1)求证:;
(2)若,,求.
【参考答案】
1.A 2.C 3.D 4.B 5.C 6.A 7.D 8.B 9.D 10.A
11.2
12.28
13.①②④
14.2
15.
16.解:(1)证明:∵四边形为平行四边形,
∴,,
∴,
∵,
∴,
∴,
在和中,,
∴≌;
(2)∵平分,
∴,
又∵,
∴,
∴为等边三角形,
∴,
∵,
∴,
∵≌,
∴,
∴.
17.证明:四边形为平行四边形,
,
,
又,
,
在和中,
,
,
,
,
即.
18.(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABE=∠CDF,
∵AE⊥ED,CF⊥BD,
∴∠AEB=∠CFD=90°,
在△ABE和△CDF中,
,
∴,
∴BE=DF,
∵OB=OD,
∴OB-BE=OD-DF,
∴OE=OF.
(2)∵AE=EF=4,
∴OE=OF=,
∴在中,,
∴.
19.(1)依题意,图中13个三角形为等边三角形
△ABC边长为x,△BMN边长为y,
AM=x+y,AK=AM=x+y, DK=x+y+x=2x+y,
DK=DO=OH,
OH=2x+y,OK=2x+y,
PK=KM=AK=x+y,
EO=OK+KP=2x+y+x+y=3x+2y,
EH=EO+OH=3x+2y+2x+y=5x+3y,
当,时,
OH=7,;
(2)由(1)得:EH=5x+3y,
FR=PN=PM+MN=x+y+y=x+2y,
RG=RB=RN+BN=FR+BN=x+2y+y=x+3y,
FG=FR+RG=x+2y+x+3y=2x+5y,
四边形是平行四边形,
EH=FG,
5x+3y=2x+5y,
整理得:3x=2y,
即x:y=2:3.
20.证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠BAE=∠DCF,
∵E,F是对角线AC的三等分点,
∴AE=CF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS),
∴BE=DF.
21.证:∵四边形ABCD是平行四边形,
∴AD=CB,AD∥BC,
∴∠ADE=∠CBF,
在△ADE和△CBF中,
∴△ADE≌△CBF(SAS),
∴∠AED=∠CFB,
∴AE∥CF.
22.(1)∵四边形ABCD是平行四边形,
∴ ,
在和中,
;
(2)如图,过点A作AG⊥BD于点G,过点C作CH⊥BD于点H,
,
.
∵四边形ABCD是平行四边形,
∴ ,
在和中,
.
底相等,高也相等,所以面积也相等,
.
底相同,高相等,所以面积也相等,
.
23.解:(1)证明:四边形是平行四边形,
.
,,
.
在和中,
.
.
(2)由(1)得:,
,
.
,
.
在中,.
