2021-2022学年人教版八年级数学下册18.1.1 平行四边形的性质 课后练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册18.1.1 平行四边形的性质 课后练习(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 318.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-19 14:07:48 | ||
图片预览



文档简介
18.1.1 平行四边形的性质
一、选择题
1.如图,在 ABCD中,∠ADC=60°,点F在CD的延长线上,连结BF,G为BF的中点,连结AG.若AB=2,BC=6,DF=3,则AG的长为( )
A.3 B. C. D.
2.有下列说法:
①平行四边形具有四边形的所有性质:②平行四边形是中心对称图形:③平行四边形的任一条对角线可把平行四边形分成两个全等的三角形;④平行四边形的两条对角线把平行四边形分成4个面积相等的小三角形.
其中正确说法的序号是( ).A.①②④ B.①③④ C.①②③ D.①②③④
3.如图,平行四边形ABCD中,两对角线交于点O,AB⊥AC,AD=5cm,OC=2cm,则对角线BD的长为( )
A.cm B.8cm C.3cm D.cm
4.如图,在平行四边形ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段EC的长度为( )
A.2 B.3 C.5 D.8
5.如图,在 ABCD中,对角线AC、BD相交于点O,过点O作OE⊥AC,交AD于点E,连接CE,若△CDE的周长为8,则 ABCD的周长为( )
A.8 B.10 C.16 D.20
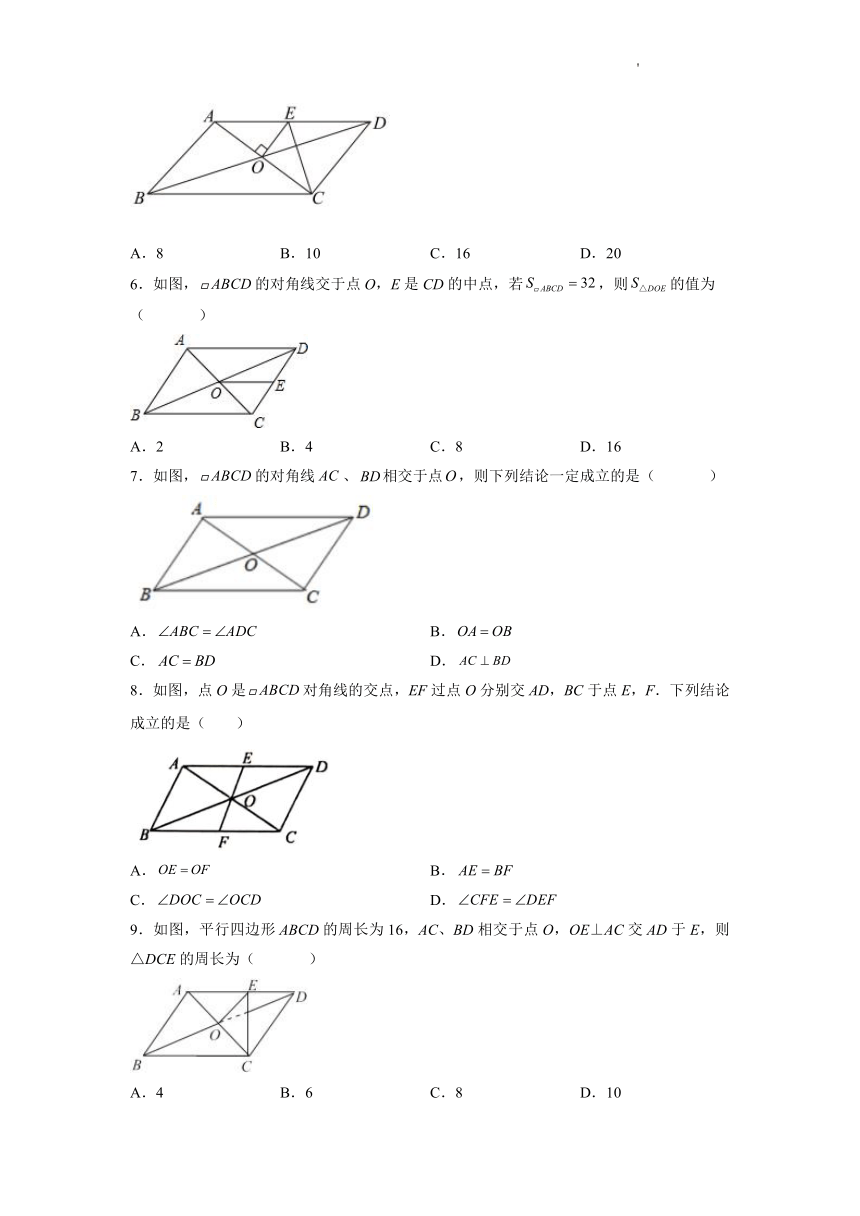
6.如图,的对角线交于点O,E是CD的中点,若,则的值为( )
A.2 B.4 C.8 D.16
7.如图,的对角线、相交于点,则下列结论一定成立的是( )
A. B.
C. D.
8.如图,点O是对角线的交点,EF过点O分别交AD,BC于点E,F.下列结论成立的是( )
A. B.
C. D.
9.如图,平行四边形ABCD的周长为16,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长为( )
A.4 B.6 C.8 D.10
10.如图,在平行四边形中,已知,,平分交边于点,则等于( )
A. B. C. D.
二、填空题
11.如图,在平行四边形ABCD中,AB=4,BC=5,以点C为圆心,适当长为半径画弧,交BC于点P,交CD于点Q,再分别以点P,Q为圆心,大于PQ的长为半径画弧,两弧相交于点N,射线CN交BA的延长线于点E,则AE的长是 _____.
12.如图,在中,.以点为圆心,以小于长为半径作弧,分别交、于点、,再分别以、为圆心,以大于的长为半径作弧,两弧在内交于点,连接并延长交于点,则____.
13.如图,直线EF经过平行四边形ABCD的对角线的交点O,若四边形AEFB的面积为20cm2,则平行四边形ABCD的面积为___cm2.
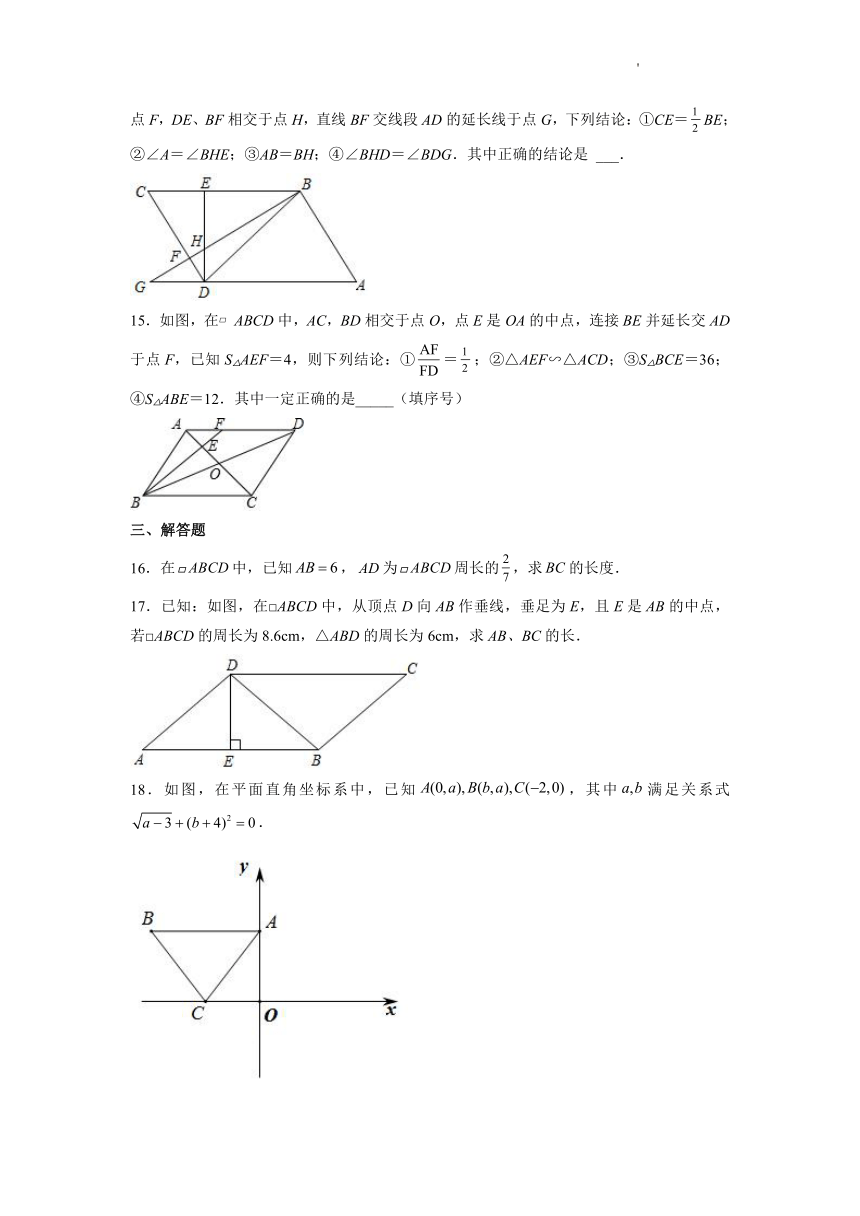
14.如图,BD为平行四边形ABCD的对角线,∠DBC=45°,DE⊥BC于点E,BF⊥CD于点F,DE、BF相交于点H,直线BF交线段AD的延长线于点G,下列结论:①CE=BE;②∠A=∠BHE;③AB=BH;④∠BHD=∠BDG.其中正确的结论是 ___.
15.如图,在 ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①=;②△AEF∽△ACD;③S△BCE=36;④S△ABE=12.其中一定正确的是_____(填序号)
三、解答题
16.在中,已知,为周长的,求的长度.
17.已知:如图,在□ABCD中,从顶点D向AB作垂线,垂足为E,且E是AB的中点,若□ABCD的周长为8.6cm,△ABD的周长为6cm,求AB、BC的长.
18.如图,在平面直角坐标系中,已知,其中满足关系式.
(1)求的值;
(2)在第三象限是否存在一点,使四边形的面积是三角形面积的倍,若存在,求出点P的坐标;若不存在,请说明理由;
(3)点D是坐标平面内的点,若点D与三点构成平行四边形,请直接写出符合条件的点D的坐标.
19.如图,在中,于点点在上,交于点,若,求的长度.
20.如图,已知口ABCD中,F是BC边的中点,连接DF并延长,交AB的延长线于点E.
求证:AB=BE.
21.已知:如图,在中,,M为的中点,连接.求证:.
22.如图1,点E为ABCD对角线AC上一点,连接DE,AE=DE=DC.
(1)求证:∠DCA=2∠ACB;
(2)如图2,若∠B=112.5°,F为线段EC上一点,且AE=EF,连接DF,设FC=x,AC=y,求y与x的函数表达式;
(3)在 (2)的条件下,如图3,点G为线段EC上(不与点E、点C重合)任意一点,试判断以DG、EG、CG为边的三角形的形状,并说明理由.
23.如图,在中,点E是上一点,和分别平分和,且,.
(1)求证:
(2)求线段的长度
(3)求平行四边形的面积.
【参考答案】
1.C 2.D 3.D 4.A 5.C 6.B 7.A 8.A 9.C 10.B
11.1
12.25゜
13.40
14.②③.
15.①③④
16.如图,
∵四边形ABCD是平行四边形,
∴CD=AB=6,AD=BC,
∵AD(AB+BC+CD+AD),
∴AD(2AD+12),
解得:AD=8,
∴BC=8;
17.解:∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,
∵□ABCD的周长为8.6cm,
∴AB+AD+BC+CD=8.6cm,
∴,
∵△ABD的周长为6cm,
∴AD+AB+BD=6cm,
∴BD=6-AD-AB=1.7cm,
∵E是AB的中点,DE⊥AB,
∴DE垂直平分线AB,
∴,
∴AB=4.3-AD=2.6cm.
18.(1)解:,
又,
且,
;
(2)存在,如图1,作CE⊥AB于点E,作PF⊥x轴于点F,
则∠BEC=90°,
由(1)得,A(0,3),B( 4,3),
∴AB∥x轴,
∴∠OCE=∠BEC=90°,
∴CE⊥x轴,
∵C( 2,0),
∴E( 2,3),
∴AB=4,CE=3,OC=2,
∴S△ABC=AB CE=×4×3=6,
∵S四边形ACPO=S△AOC+S△POC,且S四边形ACPO=S△ABC,P( 1,m)在第三象限,
∴×2×3+×2( m)=×6,
解得,m= 6,
∴P( 1, 6);
(3)如图2,平行四边形ABCD以AB、BC为邻边,
∵AB∥x轴,CD∥AB,
∴点D在x轴上,且CD=AB=4,
∴xD= 2+4=2,
∴D(2,0);
如图3,平行四边形ABDC以AB、AC为邻边,则点D在x轴上,且CD=AB=4,
∴xD= 2 4= 6,
∴D( 6,0);
如图,作CE⊥AB于点E,延长CE到点D,使DE=CE,连结AD、BD,
由(1)和(2)得,B( 4,3),E( 2,3),CE⊥x轴,
∴AE=BE,
∴四边形ADBC是平行四边形,
∵DE=CE=3,
∴CD=6,
∴D( 2,6),
综上所述,点D的坐标是(2,0)或( 6,0)或( 2,6).
19.解:
四边形是平行四边形,
.
20证明:是边的中点,
,
四边形是平行四边形,
,,
,,
在和中
,
,
,
.
21.证明:∵四边形ABCD是平行四边形,
∴AD=BC,AB∥CD,
∴∠CDM=∠AMD,∠DCM=∠BMC,
∵AB=2AD,M为AB的中点,
∴AD=AM=BM=BC,
∴∠ADM=∠AMD,∠BCM=∠BMC,
∴∠ADM=∠CDM=∠ADC,∠DCM=∠BCM=∠BCD,
∵AD∥BC,
∴∠ADC+∠BCD=180°,
∴∠CDM+∠DCM=90°,
∴∠DMC=90°,
即DM⊥MC.
22.(1)∵四边形是平行四边形,
,
,
,
;
(2)∵,
∴,
∵,
∴,
∴,
,
∴
∴
(3)设,当时
∵,,
∴
∵
∴
以DG、EG、CG为边的三角形是直角三角形;
当时,过点作于,
∴
,
以DG、EG、CG为边的三角形是直角三角形;
综上所述,以DG、EG、CG为边的三角形是直角三角形;
23.解:(1)∵四边形ABCD是平行四边形,
∴AD∥BD,
∴∠ADC+∠BCD=180°,
∵CE和DE分别平分∠BCD和∠ADC,
∴∠ADE=∠CDE,∠DCE=∠BCE,
∴∠CDE+∠DCE=90°,即DE⊥CE;
(2)由(1)可知:
AB∥CD,∠ADE=∠EDC,
∴∠CDE=∠DEA,
∴∠ADE=∠DEA,
∴AD=AE=10,
同理:BE=BC=AD=10,
∴AB=AE+EB=20;
(3)∵CE⊥DE,AB=CD=20,CE=16,
∴DE==12,
∴四边形ABCD的面积=2×△DEC的面积==192.
一、选择题
1.如图,在 ABCD中,∠ADC=60°,点F在CD的延长线上,连结BF,G为BF的中点,连结AG.若AB=2,BC=6,DF=3,则AG的长为( )
A.3 B. C. D.
2.有下列说法:
①平行四边形具有四边形的所有性质:②平行四边形是中心对称图形:③平行四边形的任一条对角线可把平行四边形分成两个全等的三角形;④平行四边形的两条对角线把平行四边形分成4个面积相等的小三角形.
其中正确说法的序号是( ).A.①②④ B.①③④ C.①②③ D.①②③④
3.如图,平行四边形ABCD中,两对角线交于点O,AB⊥AC,AD=5cm,OC=2cm,则对角线BD的长为( )
A.cm B.8cm C.3cm D.cm
4.如图,在平行四边形ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段EC的长度为( )
A.2 B.3 C.5 D.8
5.如图,在 ABCD中,对角线AC、BD相交于点O,过点O作OE⊥AC,交AD于点E,连接CE,若△CDE的周长为8,则 ABCD的周长为( )
A.8 B.10 C.16 D.20
6.如图,的对角线交于点O,E是CD的中点,若,则的值为( )
A.2 B.4 C.8 D.16
7.如图,的对角线、相交于点,则下列结论一定成立的是( )
A. B.
C. D.
8.如图,点O是对角线的交点,EF过点O分别交AD,BC于点E,F.下列结论成立的是( )
A. B.
C. D.
9.如图,平行四边形ABCD的周长为16,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长为( )
A.4 B.6 C.8 D.10
10.如图,在平行四边形中,已知,,平分交边于点,则等于( )
A. B. C. D.
二、填空题
11.如图,在平行四边形ABCD中,AB=4,BC=5,以点C为圆心,适当长为半径画弧,交BC于点P,交CD于点Q,再分别以点P,Q为圆心,大于PQ的长为半径画弧,两弧相交于点N,射线CN交BA的延长线于点E,则AE的长是 _____.
12.如图,在中,.以点为圆心,以小于长为半径作弧,分别交、于点、,再分别以、为圆心,以大于的长为半径作弧,两弧在内交于点,连接并延长交于点,则____.
13.如图,直线EF经过平行四边形ABCD的对角线的交点O,若四边形AEFB的面积为20cm2,则平行四边形ABCD的面积为___cm2.
14.如图,BD为平行四边形ABCD的对角线,∠DBC=45°,DE⊥BC于点E,BF⊥CD于点F,DE、BF相交于点H,直线BF交线段AD的延长线于点G,下列结论:①CE=BE;②∠A=∠BHE;③AB=BH;④∠BHD=∠BDG.其中正确的结论是 ___.
15.如图,在 ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①=;②△AEF∽△ACD;③S△BCE=36;④S△ABE=12.其中一定正确的是_____(填序号)
三、解答题
16.在中,已知,为周长的,求的长度.
17.已知:如图,在□ABCD中,从顶点D向AB作垂线,垂足为E,且E是AB的中点,若□ABCD的周长为8.6cm,△ABD的周长为6cm,求AB、BC的长.
18.如图,在平面直角坐标系中,已知,其中满足关系式.
(1)求的值;
(2)在第三象限是否存在一点,使四边形的面积是三角形面积的倍,若存在,求出点P的坐标;若不存在,请说明理由;
(3)点D是坐标平面内的点,若点D与三点构成平行四边形,请直接写出符合条件的点D的坐标.
19.如图,在中,于点点在上,交于点,若,求的长度.
20.如图,已知口ABCD中,F是BC边的中点,连接DF并延长,交AB的延长线于点E.
求证:AB=BE.
21.已知:如图,在中,,M为的中点,连接.求证:.
22.如图1,点E为ABCD对角线AC上一点,连接DE,AE=DE=DC.
(1)求证:∠DCA=2∠ACB;
(2)如图2,若∠B=112.5°,F为线段EC上一点,且AE=EF,连接DF,设FC=x,AC=y,求y与x的函数表达式;
(3)在 (2)的条件下,如图3,点G为线段EC上(不与点E、点C重合)任意一点,试判断以DG、EG、CG为边的三角形的形状,并说明理由.
23.如图,在中,点E是上一点,和分别平分和,且,.
(1)求证:
(2)求线段的长度
(3)求平行四边形的面积.
【参考答案】
1.C 2.D 3.D 4.A 5.C 6.B 7.A 8.A 9.C 10.B
11.1
12.25゜
13.40
14.②③.
15.①③④
16.如图,
∵四边形ABCD是平行四边形,
∴CD=AB=6,AD=BC,
∵AD(AB+BC+CD+AD),
∴AD(2AD+12),
解得:AD=8,
∴BC=8;
17.解:∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,
∵□ABCD的周长为8.6cm,
∴AB+AD+BC+CD=8.6cm,
∴,
∵△ABD的周长为6cm,
∴AD+AB+BD=6cm,
∴BD=6-AD-AB=1.7cm,
∵E是AB的中点,DE⊥AB,
∴DE垂直平分线AB,
∴,
∴AB=4.3-AD=2.6cm.
18.(1)解:,
又,
且,
;
(2)存在,如图1,作CE⊥AB于点E,作PF⊥x轴于点F,
则∠BEC=90°,
由(1)得,A(0,3),B( 4,3),
∴AB∥x轴,
∴∠OCE=∠BEC=90°,
∴CE⊥x轴,
∵C( 2,0),
∴E( 2,3),
∴AB=4,CE=3,OC=2,
∴S△ABC=AB CE=×4×3=6,
∵S四边形ACPO=S△AOC+S△POC,且S四边形ACPO=S△ABC,P( 1,m)在第三象限,
∴×2×3+×2( m)=×6,
解得,m= 6,
∴P( 1, 6);
(3)如图2,平行四边形ABCD以AB、BC为邻边,
∵AB∥x轴,CD∥AB,
∴点D在x轴上,且CD=AB=4,
∴xD= 2+4=2,
∴D(2,0);
如图3,平行四边形ABDC以AB、AC为邻边,则点D在x轴上,且CD=AB=4,
∴xD= 2 4= 6,
∴D( 6,0);
如图,作CE⊥AB于点E,延长CE到点D,使DE=CE,连结AD、BD,
由(1)和(2)得,B( 4,3),E( 2,3),CE⊥x轴,
∴AE=BE,
∴四边形ADBC是平行四边形,
∵DE=CE=3,
∴CD=6,
∴D( 2,6),
综上所述,点D的坐标是(2,0)或( 6,0)或( 2,6).
19.解:
四边形是平行四边形,
.
20证明:是边的中点,
,
四边形是平行四边形,
,,
,,
在和中
,
,
,
.
21.证明:∵四边形ABCD是平行四边形,
∴AD=BC,AB∥CD,
∴∠CDM=∠AMD,∠DCM=∠BMC,
∵AB=2AD,M为AB的中点,
∴AD=AM=BM=BC,
∴∠ADM=∠AMD,∠BCM=∠BMC,
∴∠ADM=∠CDM=∠ADC,∠DCM=∠BCM=∠BCD,
∵AD∥BC,
∴∠ADC+∠BCD=180°,
∴∠CDM+∠DCM=90°,
∴∠DMC=90°,
即DM⊥MC.
22.(1)∵四边形是平行四边形,
,
,
,
;
(2)∵,
∴,
∵,
∴,
∴,
,
∴
∴
(3)设,当时
∵,,
∴
∵
∴
以DG、EG、CG为边的三角形是直角三角形;
当时,过点作于,
∴
,
以DG、EG、CG为边的三角形是直角三角形;
综上所述,以DG、EG、CG为边的三角形是直角三角形;
23.解:(1)∵四边形ABCD是平行四边形,
∴AD∥BD,
∴∠ADC+∠BCD=180°,
∵CE和DE分别平分∠BCD和∠ADC,
∴∠ADE=∠CDE,∠DCE=∠BCE,
∴∠CDE+∠DCE=90°,即DE⊥CE;
(2)由(1)可知:
AB∥CD,∠ADE=∠EDC,
∴∠CDE=∠DEA,
∴∠ADE=∠DEA,
∴AD=AE=10,
同理:BE=BC=AD=10,
∴AB=AE+EB=20;
(3)∵CE⊥DE,AB=CD=20,CE=16,
∴DE==12,
∴四边形ABCD的面积=2×△DEC的面积==192.
