2021-2022学年人教版八年级数学下册18.1.1 平行四边形的性质 同步练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册18.1.1 平行四边形的性质 同步练习(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 245.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-19 14:07:47 | ||
图片预览

文档简介
18.1.1 平行四边形的性质 同步练习
一、选择题
1.平行四边形中,,则的度数是( )
A. B. C. D.
2.在平行四边形ABCD中,∠A比∠B大40°,那么∠D的度数为( )
A.60° B.70° C.80° D.110°
3.如图,平行四边形ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则EC等于( )
A.1 B.2 C.3 D.4
4.如图所示,四边形ABCD是平行四边形,点E在线段BC的延长线上,若∠DCE=128°,则∠A=( )
A.32° B.42° C.52° D.62°
5.如图,在平行四边形中,平分,交边于,,,则的长为( )
A.1 B.2 C.3 D.5
6.如图,在中,DE平分,,则( )
A.30° B.45° C.60° D.80°
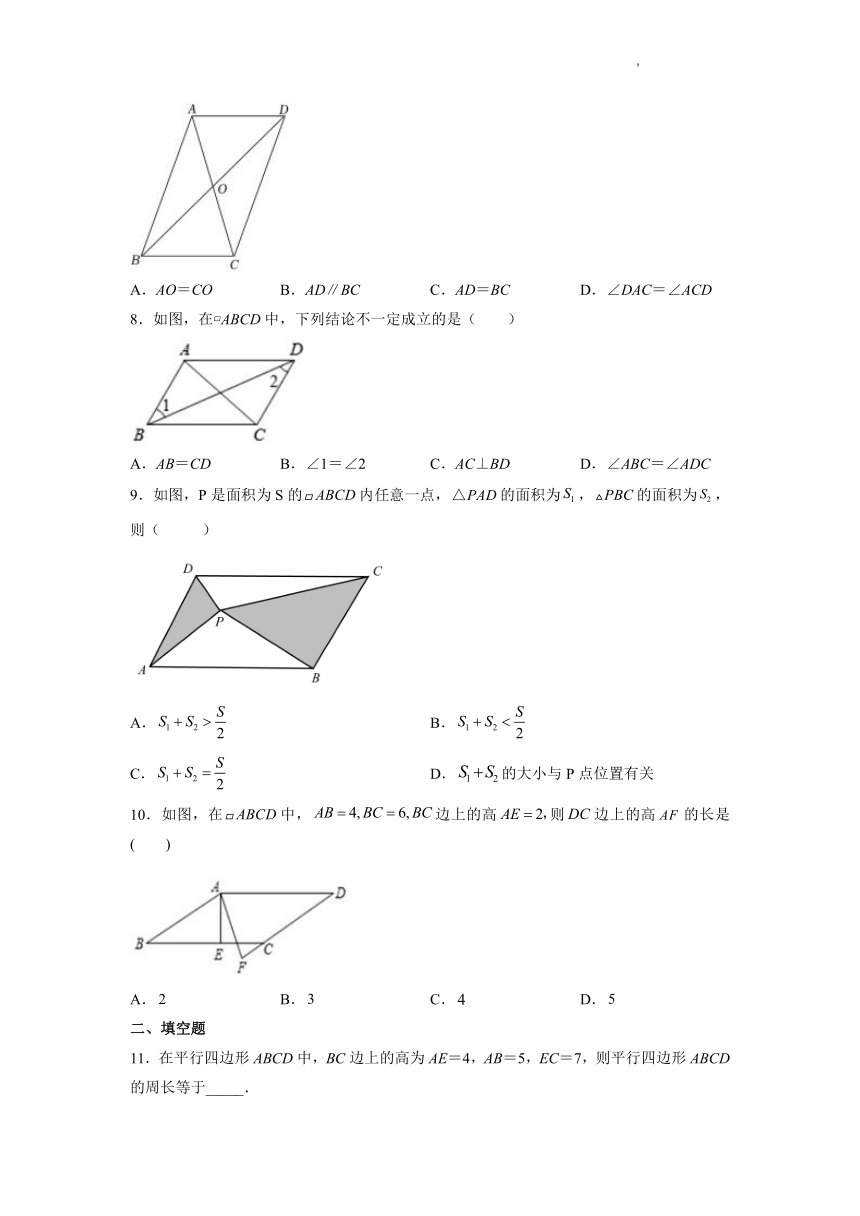
7.如图,平行四边形ABCD的对角线AC,BD相交于点O,下列结论错误的是( )
A.AO=CO B.AD∥BC C.AD=BC D.∠DAC=∠ACD
8.如图,在 ABCD中,下列结论不一定成立的是( )
A.AB=CD B.∠1=∠2 C.AC⊥BD D.∠ABC=∠ADC
9.如图,P是面积为S的内任意一点,的面积为,的面积为,则( )
A. B.
C. D.的大小与P点位置有关
10.如图,在中,边上的高则边上的高的长是( )
A. B. C. D.
二、填空题
11.在平行四边形ABCD中,BC边上的高为AE=4,AB=5,EC=7,则平行四边形ABCD的周长等于_____.
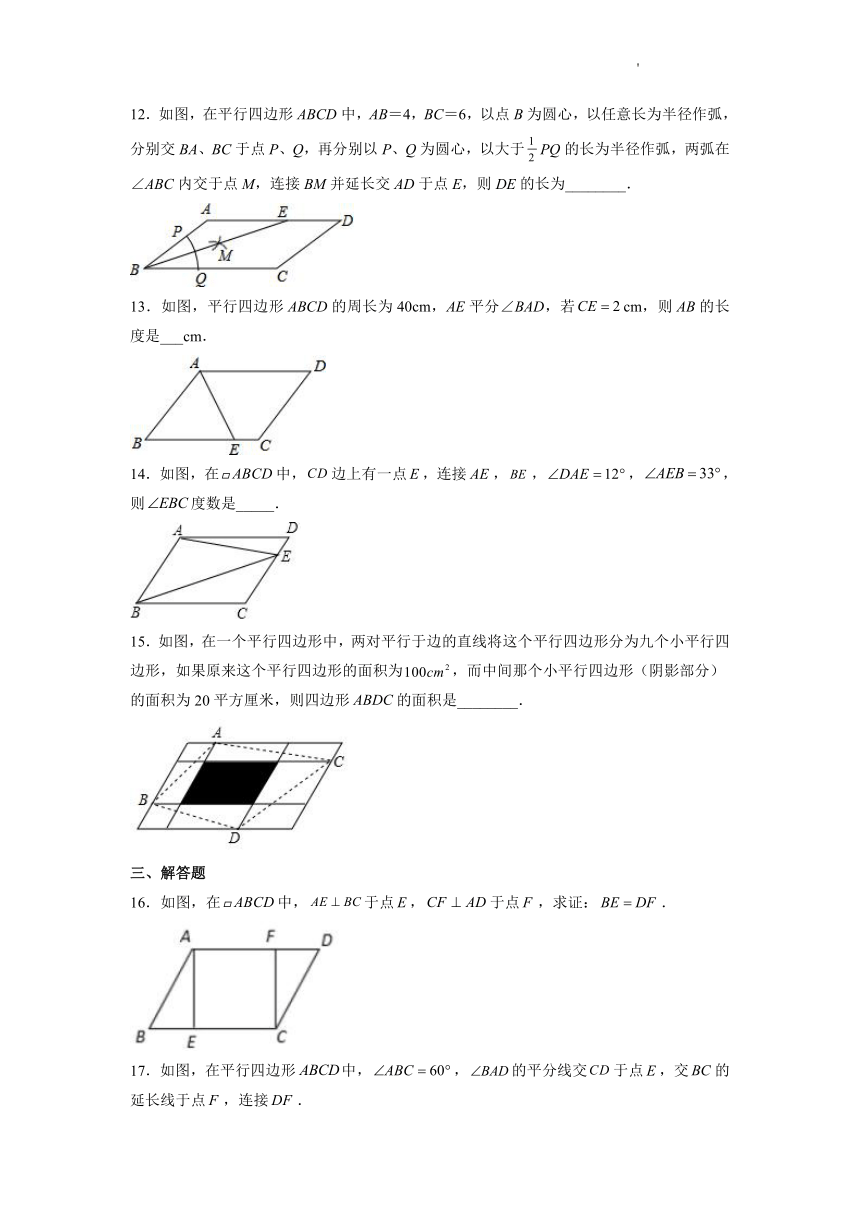
12.如图,在平行四边形ABCD中,AB=4,BC=6,以点B为圆心,以任意长为半径作弧,分别交BA、BC于点P、Q,再分别以P、Q为圆心,以大于PQ的长为半径作弧,两弧在∠ABC内交于点M,连接BM并延长交AD于点E,则DE的长为________.
13.如图,平行四边形ABCD的周长为40cm,AE平分∠BAD,若cm,则AB的长度是___cm.
14.如图,在中,边上有一点,连接,,,,则度数是_____.
15.如图,在一个平行四边形中,两对平行于边的直线将这个平行四边形分为九个小平行四边形,如果原来这个平行四边形的面积为,而中间那个小平行四边形(阴影部分)的面积为20平方厘米,则四边形的面积是________.
三、解答题
16.如图,在中,于点,于点,求证:.
17.如图,在平行四边形中,,的平分线交于点,交的延长线于点,连接.
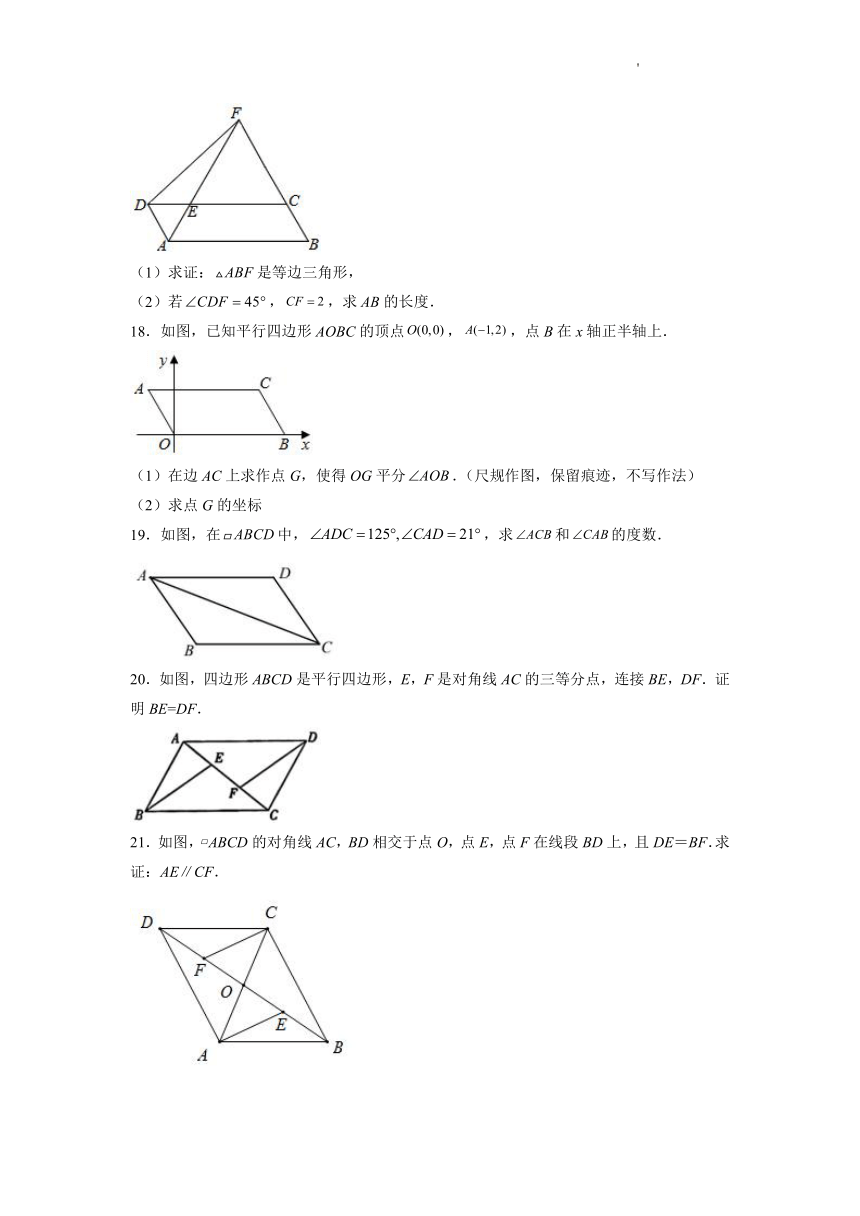
(1)求证:是等边三角形,
(2)若,,求的长度.
18.如图,已知平行四边形AOBC的顶点,,点B在x轴正半轴上.
(1)在边AC上求作点G,使得OG平分.(尺规作图,保留痕迹,不写作法)
(2)求点G的坐标
19.如图,在中,,求和的度数.
20.如图,四边形ABCD是平行四边形,E,F是对角线AC的三等分点,连接BE,DF.证明BE=DF.
21.如图, ABCD的对角线AC,BD相交于点O,点E,点F在线段BD上,且DE=BF.求证:AE∥CF.
22.如图所示,已知四边形ABCD是平行四边形,若AF、BE分别为∠DAB、∠CBA的平分线.求证:DF=EC.
23.已知,如图,在□ABCD中,AB=8cm,BC=10cm,∠C=120°,
(1)求BC边上的高AH的长;
(2)求□ABCD的面积.
【参考答案】
1.B 2.B 3.B 4.C 5.B 6.C 7.D 8.C 9.C 10.B
11.18或30
12.2
13.9
14.21°
15.60cm2.
16.证明:四边形是平行四边形,
,,
,,
在和中,
,
.
17.证明:(1)在平行四边形中,,,
∴
∵为的平分线
∴
又∵
∴是等边三角形
(2)过点作,如下图:
∵
∴,
∴为等边三角形
∴
∵
∴,
在中,,,
∴,
∵
∴
∴
∴
∴
18.解:(1)如图所示,以O为圆心,以任意长为半径画弧,分别交OA于E,OB于F,再分别以E、F为圆心,以大于EF长的一半为半径画弧,两者交于D,连接OD并延长,交AC于G,即为所求;
(2)∵四边形AOBC是平行四边形,
∴AC∥OB,
∴∠AGO=∠BOG,G的纵坐标与A相同
∵OG平分∠AOB,
∴∠AOG=∠BOG,
∴∠AOG=∠AGO,
∴AO=AG,
∵A( 1,2)
∴,
∴G的横坐标为,
∴.
19.解:∵四边形ABCD是平行四边形,∠ADC=125°,
∴AD//CB,AB∥CD,∠B=∠ADC=125°,
∴∠ACB=∠CAD,
∵∠CAD=21°,
∴∠ACB=21°,
在△ABC中,∠CAB=180°-∠B-∠ACB=180°-125°-21°=34°,
20.证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠BAE=∠DCF,
∵E,F是对角线AC的三等分点,
∴AE=CF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS),
∴BE=DF.
21.证:∵四边形ABCD是平行四边形,
∴AD=CB,AD∥BC,
∴∠ADE=∠CBF,
在△ADE和△CBF中,
∴△ADE≌△CBF(SAS),
∴∠AED=∠CFB,
∴AE∥CF.
22.证明:∵ 在ABCD中,CD∥AB,
∴ ∠DFA=∠FAB.
又∵ AF是∠DAB的平分线,
∴ ∠DAF=∠FAB,
∴ ∠DAF=∠DFA,
∴ AD=DF.
同理可得EC=BC.
∵ 在ABCD中,AD=BC,
∴ DF=EC.
23.如图所示,过A作⊥l1,使AA'等于河宽,然后连接A'B,与l2交于点N,再过N作MN⊥l1于M,
∵AA'⊥l1,MN⊥l1
∴AA'∥MN
又∵AA'=MN
∴四边形AA'NM为平行四边形
∴AM= A'N
∴AM+MN+NB= A'N+MN+NB= A'B+MN
由两点之间线段最短,可知此时路径AMNB最短
23.(1)∵在□ABCD中,AB∥CD,∴∠B=180°-120°=60°
在直角三角形ABH中,AH=AB sin=8×=.
(2)S平行四边形ABCD=BC AH=
一、选择题
1.平行四边形中,,则的度数是( )
A. B. C. D.
2.在平行四边形ABCD中,∠A比∠B大40°,那么∠D的度数为( )
A.60° B.70° C.80° D.110°
3.如图,平行四边形ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则EC等于( )
A.1 B.2 C.3 D.4
4.如图所示,四边形ABCD是平行四边形,点E在线段BC的延长线上,若∠DCE=128°,则∠A=( )
A.32° B.42° C.52° D.62°
5.如图,在平行四边形中,平分,交边于,,,则的长为( )
A.1 B.2 C.3 D.5
6.如图,在中,DE平分,,则( )
A.30° B.45° C.60° D.80°
7.如图,平行四边形ABCD的对角线AC,BD相交于点O,下列结论错误的是( )
A.AO=CO B.AD∥BC C.AD=BC D.∠DAC=∠ACD
8.如图,在 ABCD中,下列结论不一定成立的是( )
A.AB=CD B.∠1=∠2 C.AC⊥BD D.∠ABC=∠ADC
9.如图,P是面积为S的内任意一点,的面积为,的面积为,则( )
A. B.
C. D.的大小与P点位置有关
10.如图,在中,边上的高则边上的高的长是( )
A. B. C. D.
二、填空题
11.在平行四边形ABCD中,BC边上的高为AE=4,AB=5,EC=7,则平行四边形ABCD的周长等于_____.
12.如图,在平行四边形ABCD中,AB=4,BC=6,以点B为圆心,以任意长为半径作弧,分别交BA、BC于点P、Q,再分别以P、Q为圆心,以大于PQ的长为半径作弧,两弧在∠ABC内交于点M,连接BM并延长交AD于点E,则DE的长为________.
13.如图,平行四边形ABCD的周长为40cm,AE平分∠BAD,若cm,则AB的长度是___cm.
14.如图,在中,边上有一点,连接,,,,则度数是_____.
15.如图,在一个平行四边形中,两对平行于边的直线将这个平行四边形分为九个小平行四边形,如果原来这个平行四边形的面积为,而中间那个小平行四边形(阴影部分)的面积为20平方厘米,则四边形的面积是________.
三、解答题
16.如图,在中,于点,于点,求证:.
17.如图,在平行四边形中,,的平分线交于点,交的延长线于点,连接.
(1)求证:是等边三角形,
(2)若,,求的长度.
18.如图,已知平行四边形AOBC的顶点,,点B在x轴正半轴上.
(1)在边AC上求作点G,使得OG平分.(尺规作图,保留痕迹,不写作法)
(2)求点G的坐标
19.如图,在中,,求和的度数.
20.如图,四边形ABCD是平行四边形,E,F是对角线AC的三等分点,连接BE,DF.证明BE=DF.
21.如图, ABCD的对角线AC,BD相交于点O,点E,点F在线段BD上,且DE=BF.求证:AE∥CF.
22.如图所示,已知四边形ABCD是平行四边形,若AF、BE分别为∠DAB、∠CBA的平分线.求证:DF=EC.
23.已知,如图,在□ABCD中,AB=8cm,BC=10cm,∠C=120°,
(1)求BC边上的高AH的长;
(2)求□ABCD的面积.
【参考答案】
1.B 2.B 3.B 4.C 5.B 6.C 7.D 8.C 9.C 10.B
11.18或30
12.2
13.9
14.21°
15.60cm2.
16.证明:四边形是平行四边形,
,,
,,
在和中,
,
.
17.证明:(1)在平行四边形中,,,
∴
∵为的平分线
∴
又∵
∴是等边三角形
(2)过点作,如下图:
∵
∴,
∴为等边三角形
∴
∵
∴,
在中,,,
∴,
∵
∴
∴
∴
∴
18.解:(1)如图所示,以O为圆心,以任意长为半径画弧,分别交OA于E,OB于F,再分别以E、F为圆心,以大于EF长的一半为半径画弧,两者交于D,连接OD并延长,交AC于G,即为所求;
(2)∵四边形AOBC是平行四边形,
∴AC∥OB,
∴∠AGO=∠BOG,G的纵坐标与A相同
∵OG平分∠AOB,
∴∠AOG=∠BOG,
∴∠AOG=∠AGO,
∴AO=AG,
∵A( 1,2)
∴,
∴G的横坐标为,
∴.
19.解:∵四边形ABCD是平行四边形,∠ADC=125°,
∴AD//CB,AB∥CD,∠B=∠ADC=125°,
∴∠ACB=∠CAD,
∵∠CAD=21°,
∴∠ACB=21°,
在△ABC中,∠CAB=180°-∠B-∠ACB=180°-125°-21°=34°,
20.证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠BAE=∠DCF,
∵E,F是对角线AC的三等分点,
∴AE=CF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS),
∴BE=DF.
21.证:∵四边形ABCD是平行四边形,
∴AD=CB,AD∥BC,
∴∠ADE=∠CBF,
在△ADE和△CBF中,
∴△ADE≌△CBF(SAS),
∴∠AED=∠CFB,
∴AE∥CF.
22.证明:∵ 在ABCD中,CD∥AB,
∴ ∠DFA=∠FAB.
又∵ AF是∠DAB的平分线,
∴ ∠DAF=∠FAB,
∴ ∠DAF=∠DFA,
∴ AD=DF.
同理可得EC=BC.
∵ 在ABCD中,AD=BC,
∴ DF=EC.
23.如图所示,过A作⊥l1,使AA'等于河宽,然后连接A'B,与l2交于点N,再过N作MN⊥l1于M,
∵AA'⊥l1,MN⊥l1
∴AA'∥MN
又∵AA'=MN
∴四边形AA'NM为平行四边形
∴AM= A'N
∴AM+MN+NB= A'N+MN+NB= A'B+MN
由两点之间线段最短,可知此时路径AMNB最短
23.(1)∵在□ABCD中,AB∥CD,∴∠B=180°-120°=60°
在直角三角形ABH中,AH=AB sin=8×=.
(2)S平行四边形ABCD=BC AH=
