2021-2022学年人教版八年级数学下册18.2.1矩形练习 (Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册18.2.1矩形练习 (Word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 418.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-19 14:07:53 | ||
图片预览


文档简介
18.2.1矩形
一、单选题
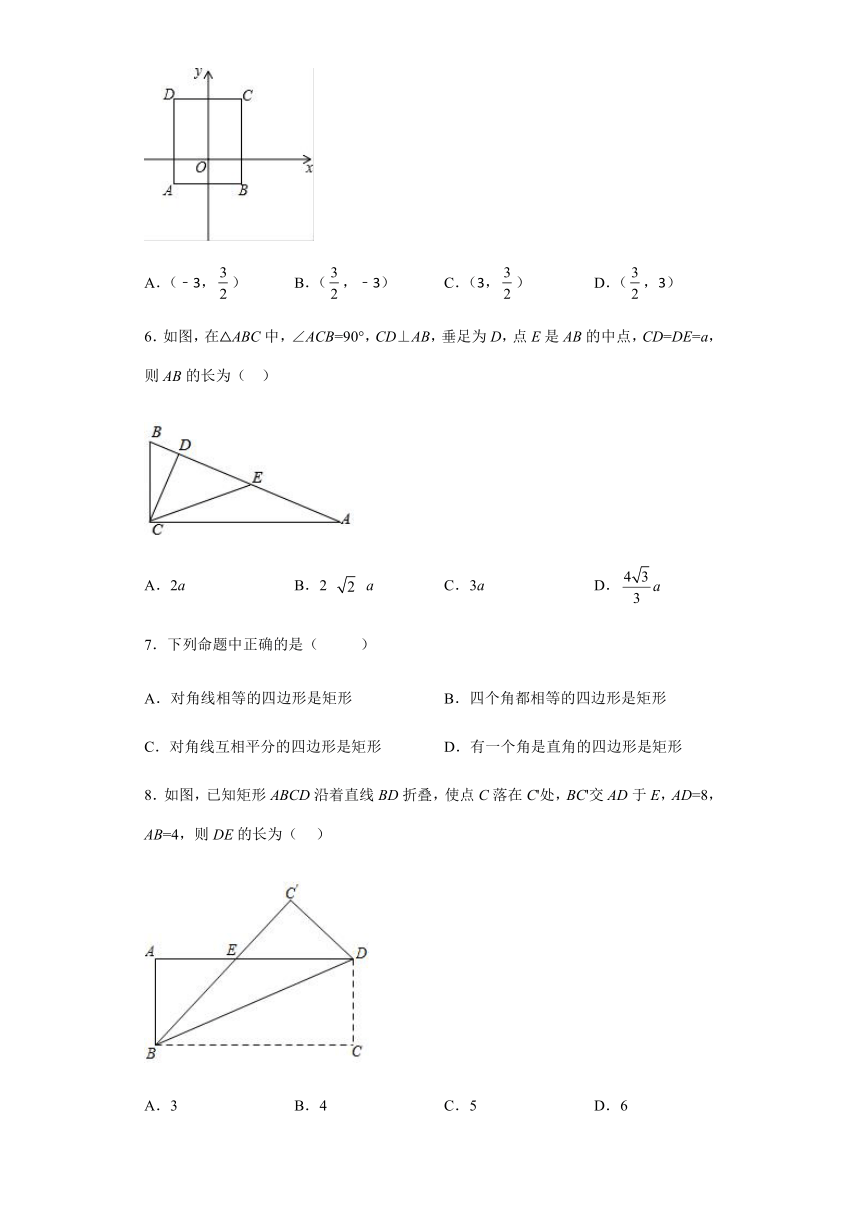
1.如图,矩形ABCD的两条对角线相交于点O,∠AOD=60°,AD=2,则AC的长是( )
A.2 B.4 C. D.
2.如图,在矩形ABCD中,对角线AC,BD相交于点O,∠ACB=30°,则∠AOB的大小为( )
A.30° B.60° C.90° D.120°
3.矩形具有而平行四边形不具有的性质是( )
A.对角线相等 B.两组对边分别平行
C.对角线互相平分 D.两组对角分别相等
4.已知一矩形的周长是24cm,相邻两边之比是1:2,那么这个矩形的面积是( )
A.24cm2 B.32cm2 C.48cm2 D.128cm2
5.如图,四边形ABCD是长方形,AB=3,AD=4.已知A(﹣,﹣1),则点C的坐标是( )
A.(﹣3,) B.(,﹣3) C.(3,) D.(,3)
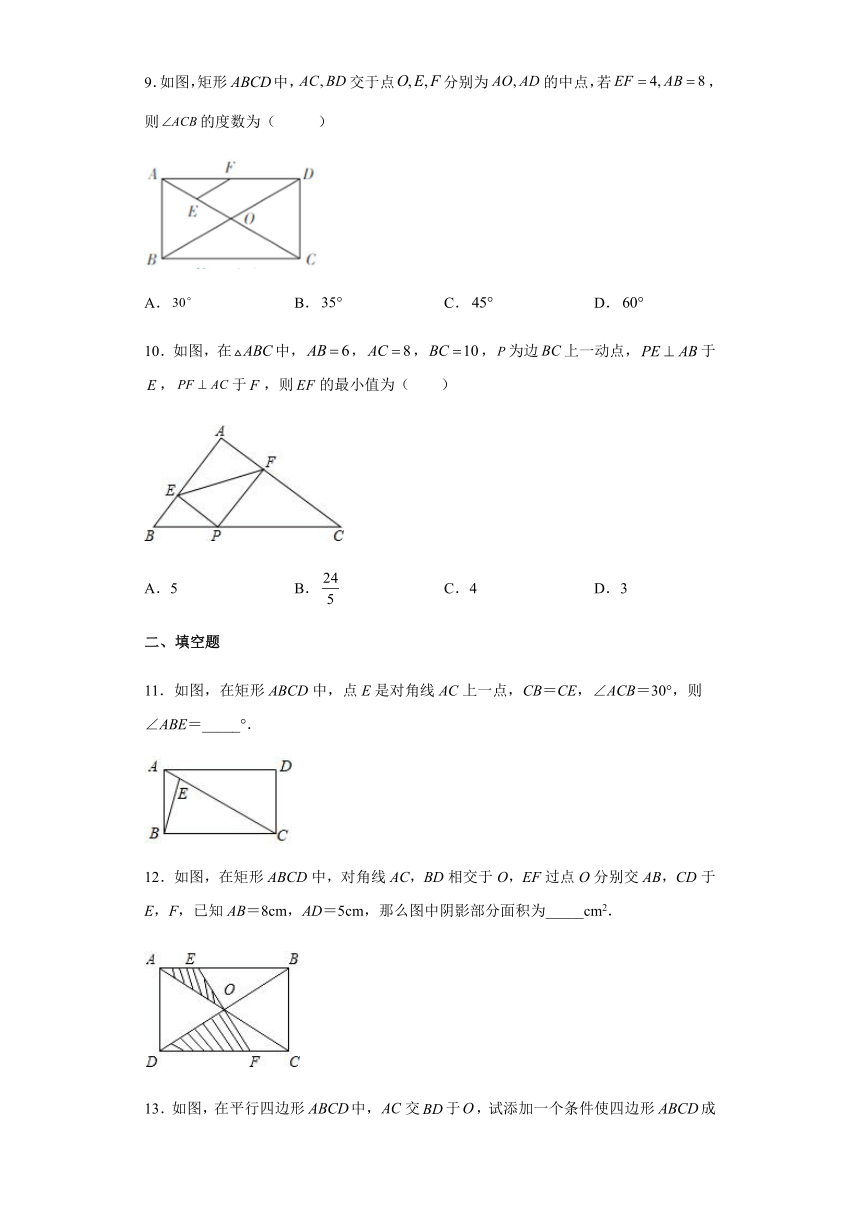
6.如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,点E是AB的中点,CD=DE=a,则AB的长为( )
A.2a B.2 a C.3a D.
7.下列命题中正确的是( )
A.对角线相等的四边形是矩形 B.四个角都相等的四边形是矩形
C.对角线互相平分的四边形是矩形 D.有一个角是直角的四边形是矩形
8.如图,已知矩形ABCD沿着直线BD折叠,使点C落在C'处,BC'交AD于E,AD=8,AB=4,则DE的长为( )
A.3 B.4 C.5 D.6
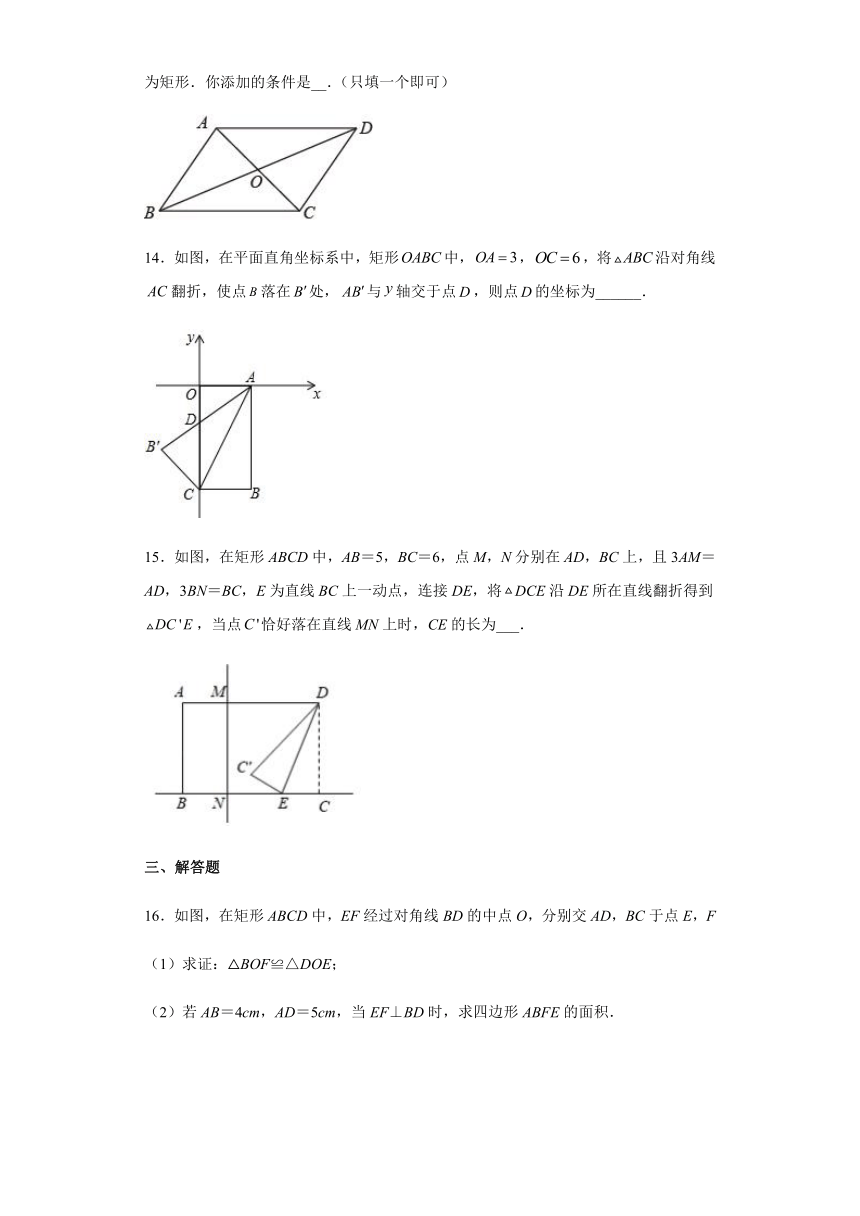
9.如图,矩形中,交于点分别为的中点,若,则的度数为( )
A. B. C. D.
10.如图,在中,,,,为边上一动点,于,于,则的最小值为( )
A.5 B. C.4 D.3
二、填空题
11.如图,在矩形ABCD中,点E是对角线AC上一点,CB=CE,∠ACB=30°,则∠ABE=_____°.
12.如图,在矩形ABCD中,对角线AC,BD相交于O,EF过点O分别交AB,CD于E,F,已知AB=8cm,AD=5cm,那么图中阴影部分面积为_____cm2.
13.如图,在平行四边形中,交于,试添加一个条件使四边形成为矩形.你添加的条件是__.(只填一个即可)
14.如图,在平面直角坐标系中,矩形中,,,将沿对角线翻折,使点落在处,与轴交于点,则点的坐标为______.
15.如图,在矩形ABCD中,AB=5,BC=6,点M,N分别在AD,BC上,且3AM=AD,3BN=BC,E为直线BC上一动点,连接DE,将DCE沿DE所在直线翻折得到,当点恰好落在直线MN上时,CE的长为___.
三、解答题
16.如图,在矩形ABCD中,EF经过对角线BD的中点O,分别交AD,BC于点E,F
(1)求证:△BOF≌△DOE;
(2)若AB=4cm,AD=5cm,当EF⊥BD时,求四边形ABFE的面积.
17.如图,四边形ABCD中,AB=CD,AD=BC,对角线AC,BD相交于点O,且OA=OD.求证:四边形ABCD是矩形.
18.如图所示,在矩形ABCD中,点E,F在BC边上,且BE=CF,求证:AF=DE
19.已知:如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,且AF=DC,连接CF.
(1)求证:D是BC的中点;
(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论.
20.(1)问题:如图1,P是矩形ABCD内任意一点,通过构造直角三角形,利用勾股定理,你能发现与的数量关系为 .
(2)探究:如图2,P是矩形ABCD外任意一点,上面的结论是否成立?若成立,请写出证明过程:若不成立,请说明理由.
(3)应用:如图3,在中,,,D是内一点,且,,求AB的最小值.
试卷第1页,共3页
答案
1.B
2.B
3.A
4.B
5.D
6.B
7.B
8.C
9.A
10.B
11.15
12.10
13.AC=BD或∠ABC=90°等
14.
15.或10
16.(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠BFO=∠DEO,∠FBO=∠EDO,
又∵O是BD中点,
∴OB=OD,
∴△BOF≌△DOE(AAS).
(2)由(1)可得ED=FB.∴AE=CF,
∴S四边形ABFE=S四边形CDEF.
又∵AB=4cm,AD=5cm
∴S矩形ABCD=20cm2,
∴S四边形ABFE=10cm2.
17.证:∵四边形ABCD中,AB=CD,AD=BC,
∴四边形ABCD是平行四边形,
∴AC=2AO,BD=2OD,
∵OA=OD,
∴AC=BD,
∴四边形ABCD是矩形.
18.解:证明:∵四边形ABCD是矩形,
∴∠B=∠C=90°,AB=CD,
∵BE=CF,
∴BE+EF=CF+EF,即BF=CE,
在△ABF和△DCE中,
,
∴△ABF≌△DCE(SAS),
∴AF=DE.
19.(1)证明:是的中点,
,
,
,.
在和中,
,
,
.
,
.
即:是的中点.
(2)解:四边形是矩形;
证明:,,
四边形是平行四边形,
,,
即,
平行四边形是矩形.
20.(1)如图,
过点P作MN垂直于AD、BC,垂足分别为M、N
由勾股定理得,
,,,
又 四边形ABCD为矩形
四边形AMNB、四边形DMNC为矩形
,
;
故答案为:;
(2)成立,理由如下:
如图,
过点P作MN垂直于AD、BC,垂足分别为M、N
由勾股定理得,
,,,
又 四边形ABCD为矩形
四边形AMNB、四边形DMNC为矩形
,
,仍然成立;
(3)如图,
以AD、BD为边作矩形ADBE,连接CE、DE
由题意得,
,,
解得
当C、D、E三点共线时,DE最小,即AB最小
的最小值 的最小值 .
答案第1页,共2页
一、单选题
1.如图,矩形ABCD的两条对角线相交于点O,∠AOD=60°,AD=2,则AC的长是( )
A.2 B.4 C. D.
2.如图,在矩形ABCD中,对角线AC,BD相交于点O,∠ACB=30°,则∠AOB的大小为( )
A.30° B.60° C.90° D.120°
3.矩形具有而平行四边形不具有的性质是( )
A.对角线相等 B.两组对边分别平行
C.对角线互相平分 D.两组对角分别相等
4.已知一矩形的周长是24cm,相邻两边之比是1:2,那么这个矩形的面积是( )
A.24cm2 B.32cm2 C.48cm2 D.128cm2
5.如图,四边形ABCD是长方形,AB=3,AD=4.已知A(﹣,﹣1),则点C的坐标是( )
A.(﹣3,) B.(,﹣3) C.(3,) D.(,3)
6.如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,点E是AB的中点,CD=DE=a,则AB的长为( )
A.2a B.2 a C.3a D.
7.下列命题中正确的是( )
A.对角线相等的四边形是矩形 B.四个角都相等的四边形是矩形
C.对角线互相平分的四边形是矩形 D.有一个角是直角的四边形是矩形
8.如图,已知矩形ABCD沿着直线BD折叠,使点C落在C'处,BC'交AD于E,AD=8,AB=4,则DE的长为( )
A.3 B.4 C.5 D.6
9.如图,矩形中,交于点分别为的中点,若,则的度数为( )
A. B. C. D.
10.如图,在中,,,,为边上一动点,于,于,则的最小值为( )
A.5 B. C.4 D.3
二、填空题
11.如图,在矩形ABCD中,点E是对角线AC上一点,CB=CE,∠ACB=30°,则∠ABE=_____°.
12.如图,在矩形ABCD中,对角线AC,BD相交于O,EF过点O分别交AB,CD于E,F,已知AB=8cm,AD=5cm,那么图中阴影部分面积为_____cm2.
13.如图,在平行四边形中,交于,试添加一个条件使四边形成为矩形.你添加的条件是__.(只填一个即可)
14.如图,在平面直角坐标系中,矩形中,,,将沿对角线翻折,使点落在处,与轴交于点,则点的坐标为______.
15.如图,在矩形ABCD中,AB=5,BC=6,点M,N分别在AD,BC上,且3AM=AD,3BN=BC,E为直线BC上一动点,连接DE,将DCE沿DE所在直线翻折得到,当点恰好落在直线MN上时,CE的长为___.
三、解答题
16.如图,在矩形ABCD中,EF经过对角线BD的中点O,分别交AD,BC于点E,F
(1)求证:△BOF≌△DOE;
(2)若AB=4cm,AD=5cm,当EF⊥BD时,求四边形ABFE的面积.
17.如图,四边形ABCD中,AB=CD,AD=BC,对角线AC,BD相交于点O,且OA=OD.求证:四边形ABCD是矩形.
18.如图所示,在矩形ABCD中,点E,F在BC边上,且BE=CF,求证:AF=DE
19.已知:如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,且AF=DC,连接CF.
(1)求证:D是BC的中点;
(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论.
20.(1)问题:如图1,P是矩形ABCD内任意一点,通过构造直角三角形,利用勾股定理,你能发现与的数量关系为 .
(2)探究:如图2,P是矩形ABCD外任意一点,上面的结论是否成立?若成立,请写出证明过程:若不成立,请说明理由.
(3)应用:如图3,在中,,,D是内一点,且,,求AB的最小值.
试卷第1页,共3页
答案
1.B
2.B
3.A
4.B
5.D
6.B
7.B
8.C
9.A
10.B
11.15
12.10
13.AC=BD或∠ABC=90°等
14.
15.或10
16.(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠BFO=∠DEO,∠FBO=∠EDO,
又∵O是BD中点,
∴OB=OD,
∴△BOF≌△DOE(AAS).
(2)由(1)可得ED=FB.∴AE=CF,
∴S四边形ABFE=S四边形CDEF.
又∵AB=4cm,AD=5cm
∴S矩形ABCD=20cm2,
∴S四边形ABFE=10cm2.
17.证:∵四边形ABCD中,AB=CD,AD=BC,
∴四边形ABCD是平行四边形,
∴AC=2AO,BD=2OD,
∵OA=OD,
∴AC=BD,
∴四边形ABCD是矩形.
18.解:证明:∵四边形ABCD是矩形,
∴∠B=∠C=90°,AB=CD,
∵BE=CF,
∴BE+EF=CF+EF,即BF=CE,
在△ABF和△DCE中,
,
∴△ABF≌△DCE(SAS),
∴AF=DE.
19.(1)证明:是的中点,
,
,
,.
在和中,
,
,
.
,
.
即:是的中点.
(2)解:四边形是矩形;
证明:,,
四边形是平行四边形,
,,
即,
平行四边形是矩形.
20.(1)如图,
过点P作MN垂直于AD、BC,垂足分别为M、N
由勾股定理得,
,,,
又 四边形ABCD为矩形
四边形AMNB、四边形DMNC为矩形
,
;
故答案为:;
(2)成立,理由如下:
如图,
过点P作MN垂直于AD、BC,垂足分别为M、N
由勾股定理得,
,,,
又 四边形ABCD为矩形
四边形AMNB、四边形DMNC为矩形
,
,仍然成立;
(3)如图,
以AD、BD为边作矩形ADBE,连接CE、DE
由题意得,
,,
解得
当C、D、E三点共线时,DE最小,即AB最小
的最小值 的最小值 .
答案第1页,共2页
