2021-2022学年人教版九年级数学下册27.2.2相似三角形的性质 同步测试 (Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册27.2.2相似三角形的性质 同步测试 (Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 152.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-19 14:11:28 | ||
图片预览



文档简介
27.2.2相似三角形的性质 同步测试
一.选择题
1.两相似三角形的周长之比为1:3,那么它们对应边上的高之比是( )
A.1:3 B.1:9 C.2:1 D.9:1
2.在△ABC中,点D、E分别为边AB、AC的中点,则△ADE与△ABC的周长之比为( )
A. B. C. D.
3.已知,它们的周长分别为30和15,且,则的长为( )
A.2 B.3 C.4 D.5
4.已知△ABC∽△DEF,若△ABC与△DEF的相似比为1∶3,则△ABC与△DEF的周长比为( )
A.1∶2 B.1∶3 C.1∶4 D.1∶9
5.如图,在平行四边形ABCD中,E是AB的中点,F是AD的中点,FE交AC于O点,交CB的延长线于G点,那么S△AOF:S△COG=( )
A.1:4 B.1:9 C.1:16 D.1:25
6.如图,AC⊥BC,AC:BC=3:4,D是AC上一点,连接BD,与∠ACB的平分线交于点E,连接AE,若S△ADE=,S△BCE=,则BC=( )
A.4 B.8 C.5 D.10
7.已知两个直角三角形的三边长分别为3,4,m和6,8,n,且这两个直角三角形不相似,则m+n的值为( )
A.10+或5+2 B.15 C.10+ D.15+3
8.如图,在△ABC中,D是CB延长线上一点,∠BAD=∠BAC.在AD上有一点E,∠EBA=∠ACB=120°.若AC=2BC=2,则DE的长为( )
A. B. C. D.
9.如图,在△ABC中,D、E分别是AB、BC上的点,且DE∥AC,若S△BDE:S△CDE=1:4,则S△BDE:S△ACD=( )
A.1:16 B.1:18 C.1:20 D.1:24
10.如图,正方形ABCD中,E,F分别在边AD,CD上,AF,BE相交于点G,若AE=3ED,DF=CF,则的值是( )
A. B. C. D.
二.填空题
11.如图,AD是△ABC的角平分线,CE是△ABC的中线,AD,CE交于点F,若∠1=∠B,则= .
12.如图,在四边形中,于点,,且,当,时,线段的长度为______.
13.如图,为平行四边形中延长线上一点,且,的外接圆交于,若,则为____.
14.如图所示,矩形中,,,,,FD=FC,则______.
15.如图,在正方形ABCD中,点P是AB上一动点(不与A、B重合),对角线AC、BD相交于点O,过点P分别作AC、BD的垂线,分别交AC、BD于点E、F,交AD、BC于点M、N.下列结论:①△APE≌△AME;②PM+PN=AC;③PE2+PF2=PO2;④△POF∽△BNF;⑤点O在M、N两点的连线上.其中正确的是 .
三.解答题
16.如图,在△ABC中,AB=AC,点P、D分别是BC、AC边上的点,且∠APD=∠B.
(1)判定△ABP与△PCD是否相似,说明理由;
(2)若AB=10,BC=12,当PD∥AB时,求BP的长.
17.如图,已知四边形ABCD是平行四边形,P为DC延长线上一点,AP分别交BD,BC于点M,N.
(1)证明:AM2=MN MP;
(2)若AD=6,DC:CP=2:1,求BN的长.
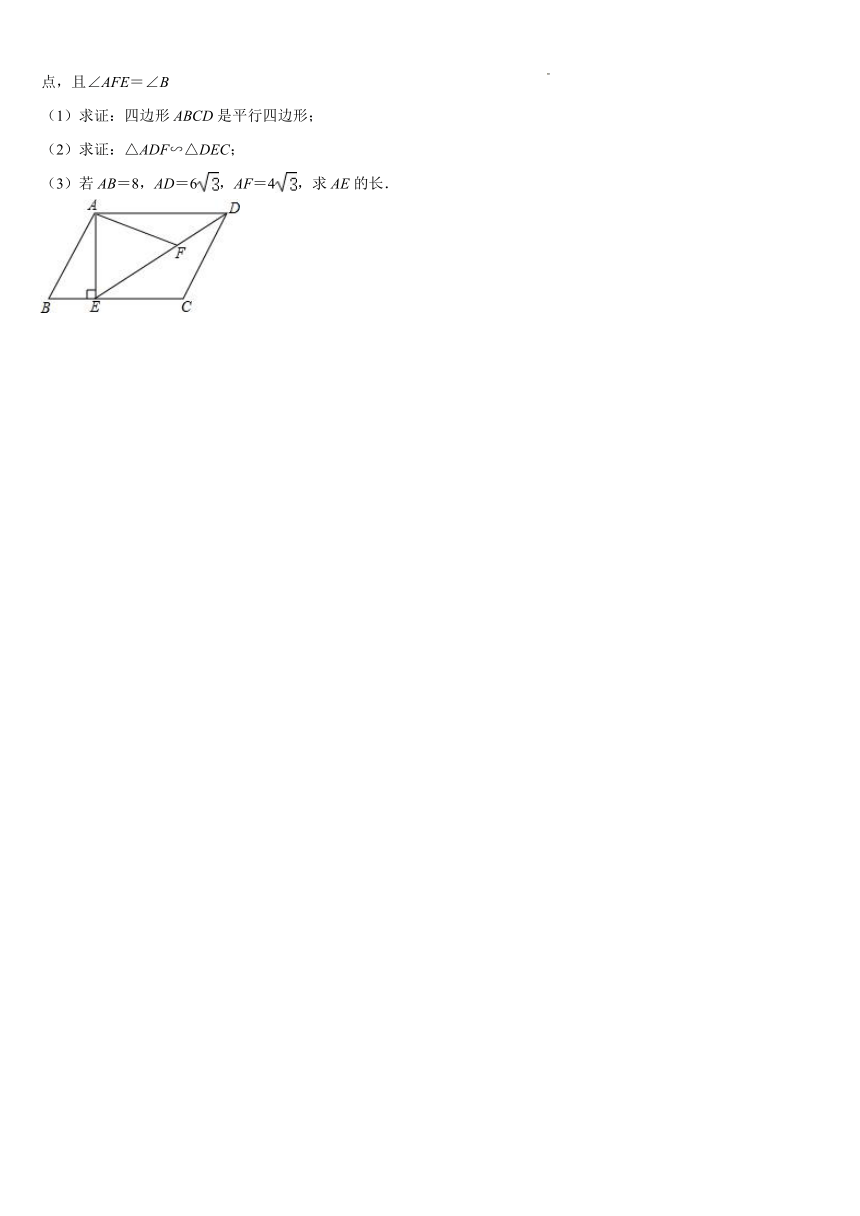
18.如图,在四边形ABCD中,AB∥CD,AD∥BC,过点A作AE⊥BC,垂足为点E,连接DE,点F为线段DE上一点,且∠AFE=∠B
(1)求证:四边形ABCD是平行四边形;
(2)求证:△ADF∽△DEC;
(3)若AB=8,AD=6,AF=4,求AE的长.
参考答案
1.A 2.A 3.B 4.B 5.B 6.B 7.A 8.C 9.C 10.C
11..
12.
13.
14.
15.①②③⑤.
16.证明:(1)∵DE∥AC,
∴∠DEB=∠FCE,
∵EF∥AB,
∴∠DBE=∠FEC,
∴△BDE∽△EFC;
(2)∵EF∥AB,
∴,
∵EC=BC﹣BE=12﹣BE,
∴,
解得:BE=4.
17.解:(1)△BAP∽△CPD,
理由如下:∵AB=AC,
∴∠ABC=∠ACB,
∵∠APC=∠ABC+∠BAP,
∴∠APD+∠DPC=∠ABC+∠BAP,
又∵∠APD=∠B,
∴∠DPC=∠BAP,
∴△BAP∽△CPD;
(2)∵PD∥AB,
∴∠APD=∠BAP,
又∵∠APD=∠B,
∴∠BAP=∠B=∠C,
又∵∠B=∠B,
∴△ABC∽△PBA,
∴,
∴,
∴BP=.
18.证明:(1)∵∠ABE=∠ACD,∠A=∠A,
∴△ABE∽△ACD,
∴;
(2)∵,
∴,
又∵∠A=∠A,
∴△ADE∽△ACB,
∴∠AED=∠ABC,
∵∠AED=∠ACD+∠CDE,∠ABC=∠ABE+∠CBE,
∴∠ACD+∠CDE=∠ABE+∠CBE,
∵∠ABE=∠ACD,
∴∠CDE=∠CBE,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠CDE=∠ABE=∠ACD,
∴DE=CE;
(3)∵CD⊥AB,
∴∠ADC=∠BDC=90°,
∴∠A+∠ACD=∠CDE+∠ADE=90°,
∵∠ABE=∠ACD,∠CDE=∠ACD,
∴∠A=∠ADE,∠BEC=∠ABE+∠A=∠A+∠ACD=90°,
∴AE=DE,BE⊥AC,
∵DE=CE,
∴AE=DE=CE,
∴AB=BC,
∵AD=2,BD=3,
∴BC=AB=AD+BD=5,
在Rt△BDC中,CD===4,
在Rt△ADC中,AC===2,
∴DE=AE=CE=,
∵∠ADC=∠GEC=90°,∠ACD=∠GCE,
∴△CGE∽△CAD,
∴,
∴GE===.
一.选择题
1.两相似三角形的周长之比为1:3,那么它们对应边上的高之比是( )
A.1:3 B.1:9 C.2:1 D.9:1
2.在△ABC中,点D、E分别为边AB、AC的中点,则△ADE与△ABC的周长之比为( )
A. B. C. D.
3.已知,它们的周长分别为30和15,且,则的长为( )
A.2 B.3 C.4 D.5
4.已知△ABC∽△DEF,若△ABC与△DEF的相似比为1∶3,则△ABC与△DEF的周长比为( )
A.1∶2 B.1∶3 C.1∶4 D.1∶9
5.如图,在平行四边形ABCD中,E是AB的中点,F是AD的中点,FE交AC于O点,交CB的延长线于G点,那么S△AOF:S△COG=( )
A.1:4 B.1:9 C.1:16 D.1:25
6.如图,AC⊥BC,AC:BC=3:4,D是AC上一点,连接BD,与∠ACB的平分线交于点E,连接AE,若S△ADE=,S△BCE=,则BC=( )
A.4 B.8 C.5 D.10
7.已知两个直角三角形的三边长分别为3,4,m和6,8,n,且这两个直角三角形不相似,则m+n的值为( )
A.10+或5+2 B.15 C.10+ D.15+3
8.如图,在△ABC中,D是CB延长线上一点,∠BAD=∠BAC.在AD上有一点E,∠EBA=∠ACB=120°.若AC=2BC=2,则DE的长为( )
A. B. C. D.
9.如图,在△ABC中,D、E分别是AB、BC上的点,且DE∥AC,若S△BDE:S△CDE=1:4,则S△BDE:S△ACD=( )
A.1:16 B.1:18 C.1:20 D.1:24
10.如图,正方形ABCD中,E,F分别在边AD,CD上,AF,BE相交于点G,若AE=3ED,DF=CF,则的值是( )
A. B. C. D.
二.填空题
11.如图,AD是△ABC的角平分线,CE是△ABC的中线,AD,CE交于点F,若∠1=∠B,则= .
12.如图,在四边形中,于点,,且,当,时,线段的长度为______.
13.如图,为平行四边形中延长线上一点,且,的外接圆交于,若,则为____.
14.如图所示,矩形中,,,,,FD=FC,则______.
15.如图,在正方形ABCD中,点P是AB上一动点(不与A、B重合),对角线AC、BD相交于点O,过点P分别作AC、BD的垂线,分别交AC、BD于点E、F,交AD、BC于点M、N.下列结论:①△APE≌△AME;②PM+PN=AC;③PE2+PF2=PO2;④△POF∽△BNF;⑤点O在M、N两点的连线上.其中正确的是 .
三.解答题
16.如图,在△ABC中,AB=AC,点P、D分别是BC、AC边上的点,且∠APD=∠B.
(1)判定△ABP与△PCD是否相似,说明理由;
(2)若AB=10,BC=12,当PD∥AB时,求BP的长.
17.如图,已知四边形ABCD是平行四边形,P为DC延长线上一点,AP分别交BD,BC于点M,N.
(1)证明:AM2=MN MP;
(2)若AD=6,DC:CP=2:1,求BN的长.
18.如图,在四边形ABCD中,AB∥CD,AD∥BC,过点A作AE⊥BC,垂足为点E,连接DE,点F为线段DE上一点,且∠AFE=∠B
(1)求证:四边形ABCD是平行四边形;
(2)求证:△ADF∽△DEC;
(3)若AB=8,AD=6,AF=4,求AE的长.
参考答案
1.A 2.A 3.B 4.B 5.B 6.B 7.A 8.C 9.C 10.C
11..
12.
13.
14.
15.①②③⑤.
16.证明:(1)∵DE∥AC,
∴∠DEB=∠FCE,
∵EF∥AB,
∴∠DBE=∠FEC,
∴△BDE∽△EFC;
(2)∵EF∥AB,
∴,
∵EC=BC﹣BE=12﹣BE,
∴,
解得:BE=4.
17.解:(1)△BAP∽△CPD,
理由如下:∵AB=AC,
∴∠ABC=∠ACB,
∵∠APC=∠ABC+∠BAP,
∴∠APD+∠DPC=∠ABC+∠BAP,
又∵∠APD=∠B,
∴∠DPC=∠BAP,
∴△BAP∽△CPD;
(2)∵PD∥AB,
∴∠APD=∠BAP,
又∵∠APD=∠B,
∴∠BAP=∠B=∠C,
又∵∠B=∠B,
∴△ABC∽△PBA,
∴,
∴,
∴BP=.
18.证明:(1)∵∠ABE=∠ACD,∠A=∠A,
∴△ABE∽△ACD,
∴;
(2)∵,
∴,
又∵∠A=∠A,
∴△ADE∽△ACB,
∴∠AED=∠ABC,
∵∠AED=∠ACD+∠CDE,∠ABC=∠ABE+∠CBE,
∴∠ACD+∠CDE=∠ABE+∠CBE,
∵∠ABE=∠ACD,
∴∠CDE=∠CBE,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠CDE=∠ABE=∠ACD,
∴DE=CE;
(3)∵CD⊥AB,
∴∠ADC=∠BDC=90°,
∴∠A+∠ACD=∠CDE+∠ADE=90°,
∵∠ABE=∠ACD,∠CDE=∠ACD,
∴∠A=∠ADE,∠BEC=∠ABE+∠A=∠A+∠ACD=90°,
∴AE=DE,BE⊥AC,
∵DE=CE,
∴AE=DE=CE,
∴AB=BC,
∵AD=2,BD=3,
∴BC=AB=AD+BD=5,
在Rt△BDC中,CD===4,
在Rt△ADC中,AC===2,
∴DE=AE=CE=,
∵∠ADC=∠GEC=90°,∠ACD=∠GCE,
∴△CGE∽△CAD,
∴,
∴GE===.
