北师大版八年级数学下册 第4章因式分解回顾与思考 课件(共17张PPT)
文档属性
| 名称 | 北师大版八年级数学下册 第4章因式分解回顾与思考 课件(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 617.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-19 16:03:31 | ||
图片预览





文档简介
(共17张PPT)
因式分解
回顾与思考
1、举例说明什么是分解因式。
2、分解因式与整式乘法有什么关系?
3、分解因式常用的方法有哪些?
4、试着画出本章的知识结构图。
知识回顾
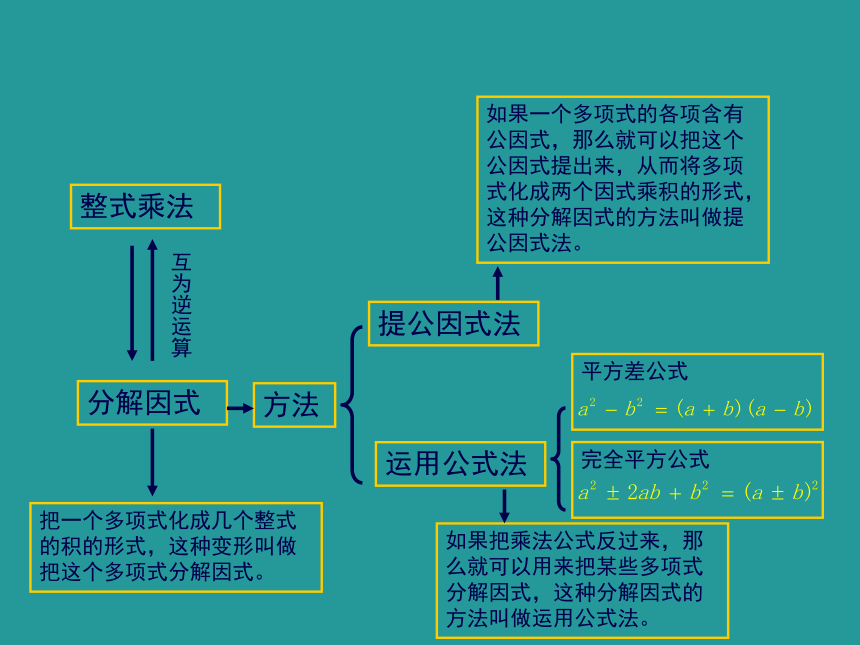
把一个多项式化成几个整式的积的形式,这种变形叫做把这个多项式分解因式。
分解因式
方法
提公因式法
运用公式法
整式乘法
互为逆运算
如果一个多项式的各项含有公因式,那么就可以把这个公因式提出来,从而将多项式化成两个因式乘积的形式,这种分解因式的方法叫做提公因式法。
如果把乘法公式反过来,那么就可以用来把某些多项式分解因式,这种分解因式的方法叫做运用公式法。
平方差公式
完全平方公式
知识点一:对分解因式概念的理解
例1.下列式子从左到右的变形中是分解因式的为( )。
A.
B.
C.
D.
B
A选项没有化成几个整式的积的形式;
B选项运用完全平方公式;
C选项属于整式乘法;
D选项没有化成几个整式的积的形式.`
总结归纳
知识点二:利用提公因式法分解因式
例2.把下列各式分解因式
⑴
解:原式
⑵
解:原式
公因式既可以是单
项式,也可以是多
项式,需要整体把
握。
例3.把下列各式分解因式
⑴ ⑵
解:原式 解:原式
⑶ ⑷
解:原式 解:原式
知识点三:利用公式法分解因式
可以先化简整理,再
考虑用公式或其它
方法进行因式分解。
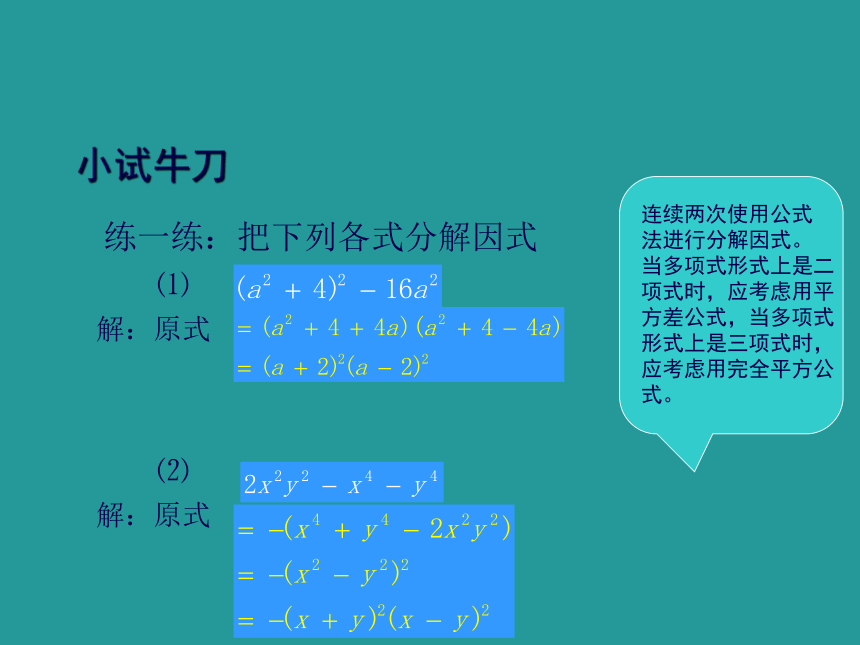
小试牛刀
练一练:把下列各式分解因式
⑴
解:原式
⑵
解:原式
连续两次使用公式
法进行分解因式。
当多项式形式上是二
项式时,应考虑用平
方差公式,当多项式
形式上是三项式时,
应考虑用完全平方公
式。
知识点四:综合运用多种方法分解因式
例4.把下列各式分解因式
⑴ ⑵
解:原式 解:原式
⑶ ⑷
解:原式 解:原式
先观察是否有公因式,若有公因式提出后
看是否具有平方差公式或完全平方公式特
征,若有使用公式法;若都没有,则考虑
将多项式进行重新整理或分组后进行分解
因式。
知识点五:运用分解因式进行计算和求值
例5.利用分解因式计算
⑴ ⑵
解:原式 解:原式
⑶
解:原式
例6.已知 ,求 的值。
解:
例7.已知 ,求 的值。
解:
例8.计算下列各式:
你能根据所学知识找到计算上面算式的简便方法吗?请你利用你找到的简便方法计算下式:
知识点六:分解因式的实际应用
例9.如图,在一个半径为R的圆形钢板上,机械加工时冲去半径为r的四个小圆.
(1)用代数式表示剩余部分的面积;
(2)用简便方法计算:当R=7.5,r=1.25时,剩余部分的面积.
(2)当R=7.5,r=1.25时,
S=πR2 –4πr2
=π(R+2r)(R –2r)
=π(7.5+2×1.25)(7.5 –2×1.25)
=π×10×5=50π
解:(1)S=πR2 –4πr2
能力提升
1.正方形Ⅰ的周长比正方形Ⅱ的周长长96cm,它们的面积相差960cm2.求这两个正方形的边长。
活学活用
解:设正方形Ⅰ的边长为x cm,正方形Ⅱ的边长为y cm;
列方程得: 化简得:
整理得: 解得:
答:两个正方形的边长分别为32cm,8cm.
2.当x取何值时,x2+2x+1取得最小值?
3.当k取何值时,100 x2-kxy+49y2是一个完全平方式?
2. 解:x2+2x+1=(x+1)2
当x=-1时, x2+2x+1取得最小值0。
3.解:100 x2-kxy+49y2
=(10x)2-kxy+(7y)2
所以k=±2×10×7=±140
例10.利用分解因式说明: 能被120整除。
提示:底数不同,且指数不全为偶数,若考虑使用平方差公式则需要 转化底数。
解:
永攀高峰:
可以被60和70之间某两个自然数整除,
求这两个数。
答:这两个数分别为65和63。
解:
反复利用平方差公
式进行分解因式,
分解过程中需注意
题目中的条件要求,
分解因式“适可而止”。
作业
完成书上习题
因式分解
回顾与思考
1、举例说明什么是分解因式。
2、分解因式与整式乘法有什么关系?
3、分解因式常用的方法有哪些?
4、试着画出本章的知识结构图。
知识回顾
把一个多项式化成几个整式的积的形式,这种变形叫做把这个多项式分解因式。
分解因式
方法
提公因式法
运用公式法
整式乘法
互为逆运算
如果一个多项式的各项含有公因式,那么就可以把这个公因式提出来,从而将多项式化成两个因式乘积的形式,这种分解因式的方法叫做提公因式法。
如果把乘法公式反过来,那么就可以用来把某些多项式分解因式,这种分解因式的方法叫做运用公式法。
平方差公式
完全平方公式
知识点一:对分解因式概念的理解
例1.下列式子从左到右的变形中是分解因式的为( )。
A.
B.
C.
D.
B
A选项没有化成几个整式的积的形式;
B选项运用完全平方公式;
C选项属于整式乘法;
D选项没有化成几个整式的积的形式.`
总结归纳
知识点二:利用提公因式法分解因式
例2.把下列各式分解因式
⑴
解:原式
⑵
解:原式
公因式既可以是单
项式,也可以是多
项式,需要整体把
握。
例3.把下列各式分解因式
⑴ ⑵
解:原式 解:原式
⑶ ⑷
解:原式 解:原式
知识点三:利用公式法分解因式
可以先化简整理,再
考虑用公式或其它
方法进行因式分解。
小试牛刀
练一练:把下列各式分解因式
⑴
解:原式
⑵
解:原式
连续两次使用公式
法进行分解因式。
当多项式形式上是二
项式时,应考虑用平
方差公式,当多项式
形式上是三项式时,
应考虑用完全平方公
式。
知识点四:综合运用多种方法分解因式
例4.把下列各式分解因式
⑴ ⑵
解:原式 解:原式
⑶ ⑷
解:原式 解:原式
先观察是否有公因式,若有公因式提出后
看是否具有平方差公式或完全平方公式特
征,若有使用公式法;若都没有,则考虑
将多项式进行重新整理或分组后进行分解
因式。
知识点五:运用分解因式进行计算和求值
例5.利用分解因式计算
⑴ ⑵
解:原式 解:原式
⑶
解:原式
例6.已知 ,求 的值。
解:
例7.已知 ,求 的值。
解:
例8.计算下列各式:
你能根据所学知识找到计算上面算式的简便方法吗?请你利用你找到的简便方法计算下式:
知识点六:分解因式的实际应用
例9.如图,在一个半径为R的圆形钢板上,机械加工时冲去半径为r的四个小圆.
(1)用代数式表示剩余部分的面积;
(2)用简便方法计算:当R=7.5,r=1.25时,剩余部分的面积.
(2)当R=7.5,r=1.25时,
S=πR2 –4πr2
=π(R+2r)(R –2r)
=π(7.5+2×1.25)(7.5 –2×1.25)
=π×10×5=50π
解:(1)S=πR2 –4πr2
能力提升
1.正方形Ⅰ的周长比正方形Ⅱ的周长长96cm,它们的面积相差960cm2.求这两个正方形的边长。
活学活用
解:设正方形Ⅰ的边长为x cm,正方形Ⅱ的边长为y cm;
列方程得: 化简得:
整理得: 解得:
答:两个正方形的边长分别为32cm,8cm.
2.当x取何值时,x2+2x+1取得最小值?
3.当k取何值时,100 x2-kxy+49y2是一个完全平方式?
2. 解:x2+2x+1=(x+1)2
当x=-1时, x2+2x+1取得最小值0。
3.解:100 x2-kxy+49y2
=(10x)2-kxy+(7y)2
所以k=±2×10×7=±140
例10.利用分解因式说明: 能被120整除。
提示:底数不同,且指数不全为偶数,若考虑使用平方差公式则需要 转化底数。
解:
永攀高峰:
可以被60和70之间某两个自然数整除,
求这两个数。
答:这两个数分别为65和63。
解:
反复利用平方差公
式进行分解因式,
分解过程中需注意
题目中的条件要求,
分解因式“适可而止”。
作业
完成书上习题
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
