北师大版八年级数学下册 第五章 分式与分式方程 回顾与思考 课件(共21张PPT)
文档属性
| 名称 | 北师大版八年级数学下册 第五章 分式与分式方程 回顾与思考 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 610.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-19 15:28:38 | ||
图片预览








文档简介
(共21张PPT)
第五章分式回顾与思考(一)
北师大版
八年级下册
本章知识网络
分式
1、分式概念
2、分式的基本性质
3、分式的运算
4、分式方程
⑴分式有意义的条件
⑵分式的值为0的条件
分式的约分
分式的通分
分式的乘除法运算
分式的加减法运算
分式方程的解法步骤
分式方程的应用
1.分式的定义:
2.分式有意义的条件:
B≠0
分式无意义的条件:
B = 0
3.分式值为 0 的条件:
A=0且 B ≠0
A>0 ,B>0 或 A<0, B<0
A>0 ,B<0 或 A<0 ,B>0
分式 < 0 的条件:
A
B
4.分式 > 0 的条件:
A
B
A
B
形如 的式子 ,其中 A ,B 都是整式,
且 B 中含有字母.
一、分式的概念:
5.下列各式(1) (2) (3) (4) (5)
是分式的有 个。
1
2x
3
2x
x
2x2
1-
3
2x
6.下列各式中x 取何值时,分式有意义.
(1) (2) (3) (4)
X - 5
X + 2
X2 -4
4x
X -1
2
X2 + 2
1
巩固提升:
3
x ≠-2
x≠±1
x ≠±2
x 为一切实数
7.当x 时,分式 的值是负数.
X2+3
X+2
<-2
8.当x 时,分式 的值是非负数.
X-7
X+1
≥7或<-1
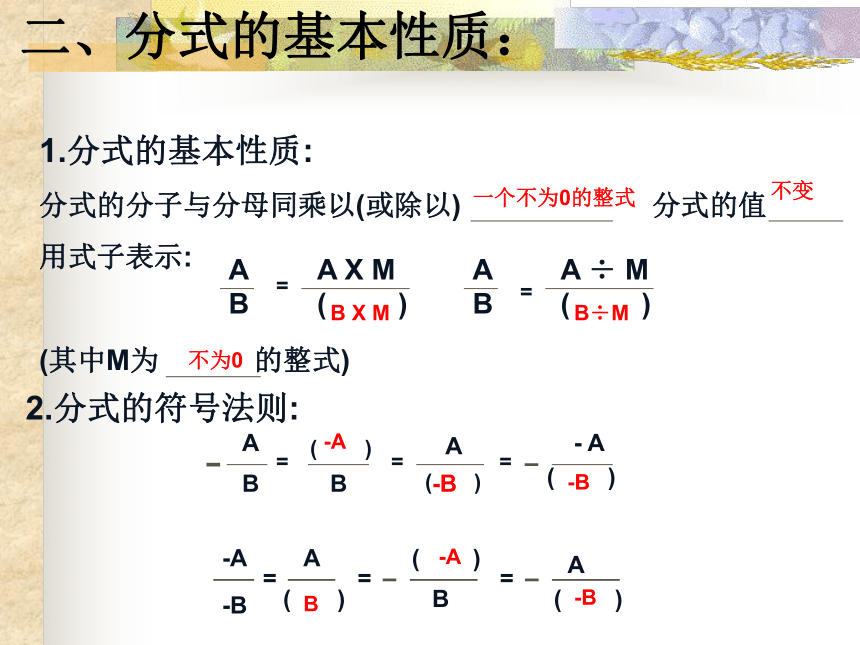
1.分式的基本性质:
分式的分子与分母同乘以(或除以) 分式的值
用式子表示:
(其中M为 的整式)
A
B
A X M
( )
A
B
A ÷ M
( )
=
=
2.分式的符号法则:
A
B
=
B
( )
=
A
( )
=
- A
( )
-A
-B
=
A
( )
=
B
( )
=
A
( )
一个不为0的整式
不变
B X M
B÷M
不为0
-A
-B
-B
B
-A
-B
二、分式的基本性质:
1.写出下列等式中的未知的分子或分母.
(2)
(3) (4)
a+b
ab
=
a2b
( )
ab+b2
ab2+b
=
a+b
( )
a -b
a+b
=
a2 –b2
( )
a+b
ab
=
2a2+2ab
( )
a2+ab
ab+1
a2+b2-2ab
2a2b
巩固提升:
2.下列变形正确的是( )
A B
C D
a
b
=
a2
b2
a-b
a
=
a2-b
a2
2-x
X-1
=
X-2
1-x
4
2a+b
=
2
a+b
C
3.如果把分式 中的x和y的值都扩大3倍,
则分式的值( )
A 扩大3倍 B不变 C缩小1/3 D缩小1/6
x
x+y
B
巩固提升:
1.约分:
把分子、分母的最大公因式(数)约去。
三、分式的约分和通分:
2.约分:
(1) (2)
(3)
-3x2y
27xy2
-4(a-b)2
-16(b-a)3
m2+4m+4
m2 - 4
2.通分:(确定下列各式的最简公分母)
(1) (2)
x
6a2b
与
y
4ab2c
a-2
a2+2a+1
与
2
a2-1
约分与通分的依据都是:
分式的基本性质
把分母不相同的几个分式化成分母相同的分式。
2.通分:
通分的关键是找最简公分母。
定系数:
最简公分母的确定方法:定字母:
定次数:
各分母的最小公倍数;
同一字母的最高次。
分母中所以字母都取;
四、分式的乘除:
分式的加减
同分母相加
异分母相加
通分
五、分式的加减:
能力提升
(4) ;
巩固提升
1. 已知 x2 – 3x+1=0 ,求 x2+ 的值.
1
x2
2.已知 x2 - 4x =1 ,求 的值.
x2
x4+x2+1
拓展延伸
3.化简求值
原式
小结提升:
分式
1、分式概念
2、分式的基本性质
3、分式的运算
⑴分式有意义的条件
⑵分式的值为0的条件
分式的约分
分式的通分
分式的乘除法运算
分式的加减法运算
同分母分式
异分母分式
1.如果把分式 中的x和y的值都扩大3倍,
则分式的值( )
A.扩大3倍 B.不变 C.缩小 D.缩小
xy
x+y
A
检测反馈:
2. 若分式
若有意义,则x应满足( )
B
若值为0,则x应满足( )
A、x≠-1 B、x ≠-1且x ≠2
C、x≠2 D、x ≠-1或x ≠2
A、x=2 B、x =-2
C、 x=±2 D、x =-1或x =2
B
检测反馈:
3. 化简: + + + .
解:原式=
=
=
=
检测反馈:
4.已知 ,求 的值.
1
x
+
1
y
=
5
2x-3xy+2y
-x+2xy-y
检测反馈:
5.已知 ,试求 的值.
x
2
=
y
3
=
Z
4
x+y-z
x+y+z
6.已知 求A、B
A=1,B=5
再见!
检测反馈:
第五章分式回顾与思考(一)
北师大版
八年级下册
本章知识网络
分式
1、分式概念
2、分式的基本性质
3、分式的运算
4、分式方程
⑴分式有意义的条件
⑵分式的值为0的条件
分式的约分
分式的通分
分式的乘除法运算
分式的加减法运算
分式方程的解法步骤
分式方程的应用
1.分式的定义:
2.分式有意义的条件:
B≠0
分式无意义的条件:
B = 0
3.分式值为 0 的条件:
A=0且 B ≠0
A>0 ,B>0 或 A<0, B<0
A>0 ,B<0 或 A<0 ,B>0
分式 < 0 的条件:
A
B
4.分式 > 0 的条件:
A
B
A
B
形如 的式子 ,其中 A ,B 都是整式,
且 B 中含有字母.
一、分式的概念:
5.下列各式(1) (2) (3) (4) (5)
是分式的有 个。
1
2x
3
2x
x
2x2
1-
3
2x
6.下列各式中x 取何值时,分式有意义.
(1) (2) (3) (4)
X - 5
X + 2
X2 -4
4x
X -1
2
X2 + 2
1
巩固提升:
3
x ≠-2
x≠±1
x ≠±2
x 为一切实数
7.当x 时,分式 的值是负数.
X2+3
X+2
<-2
8.当x 时,分式 的值是非负数.
X-7
X+1
≥7或<-1
1.分式的基本性质:
分式的分子与分母同乘以(或除以) 分式的值
用式子表示:
(其中M为 的整式)
A
B
A X M
( )
A
B
A ÷ M
( )
=
=
2.分式的符号法则:
A
B
=
B
( )
=
A
( )
=
- A
( )
-A
-B
=
A
( )
=
B
( )
=
A
( )
一个不为0的整式
不变
B X M
B÷M
不为0
-A
-B
-B
B
-A
-B
二、分式的基本性质:
1.写出下列等式中的未知的分子或分母.
(2)
(3) (4)
a+b
ab
=
a2b
( )
ab+b2
ab2+b
=
a+b
( )
a -b
a+b
=
a2 –b2
( )
a+b
ab
=
2a2+2ab
( )
a2+ab
ab+1
a2+b2-2ab
2a2b
巩固提升:
2.下列变形正确的是( )
A B
C D
a
b
=
a2
b2
a-b
a
=
a2-b
a2
2-x
X-1
=
X-2
1-x
4
2a+b
=
2
a+b
C
3.如果把分式 中的x和y的值都扩大3倍,
则分式的值( )
A 扩大3倍 B不变 C缩小1/3 D缩小1/6
x
x+y
B
巩固提升:
1.约分:
把分子、分母的最大公因式(数)约去。
三、分式的约分和通分:
2.约分:
(1) (2)
(3)
-3x2y
27xy2
-4(a-b)2
-16(b-a)3
m2+4m+4
m2 - 4
2.通分:(确定下列各式的最简公分母)
(1) (2)
x
6a2b
与
y
4ab2c
a-2
a2+2a+1
与
2
a2-1
约分与通分的依据都是:
分式的基本性质
把分母不相同的几个分式化成分母相同的分式。
2.通分:
通分的关键是找最简公分母。
定系数:
最简公分母的确定方法:定字母:
定次数:
各分母的最小公倍数;
同一字母的最高次。
分母中所以字母都取;
四、分式的乘除:
分式的加减
同分母相加
异分母相加
通分
五、分式的加减:
能力提升
(4) ;
巩固提升
1. 已知 x2 – 3x+1=0 ,求 x2+ 的值.
1
x2
2.已知 x2 - 4x =1 ,求 的值.
x2
x4+x2+1
拓展延伸
3.化简求值
原式
小结提升:
分式
1、分式概念
2、分式的基本性质
3、分式的运算
⑴分式有意义的条件
⑵分式的值为0的条件
分式的约分
分式的通分
分式的乘除法运算
分式的加减法运算
同分母分式
异分母分式
1.如果把分式 中的x和y的值都扩大3倍,
则分式的值( )
A.扩大3倍 B.不变 C.缩小 D.缩小
xy
x+y
A
检测反馈:
2. 若分式
若有意义,则x应满足( )
B
若值为0,则x应满足( )
A、x≠-1 B、x ≠-1且x ≠2
C、x≠2 D、x ≠-1或x ≠2
A、x=2 B、x =-2
C、 x=±2 D、x =-1或x =2
B
检测反馈:
3. 化简: + + + .
解:原式=
=
=
=
检测反馈:
4.已知 ,求 的值.
1
x
+
1
y
=
5
2x-3xy+2y
-x+2xy-y
检测反馈:
5.已知 ,试求 的值.
x
2
=
y
3
=
Z
4
x+y-z
x+y+z
6.已知 求A、B
A=1,B=5
再见!
检测反馈:
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
