北师大版八年级数学下册 6.1 平行四边形的性质 课件(共30张PPT)
文档属性
| 名称 | 北师大版八年级数学下册 6.1 平行四边形的性质 课件(共30张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 999.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-19 15:57:01 | ||
图片预览









文档简介
(共30张PPT)
平行四边形的性质1
平行四边形特征的探索
做一做 :小组活动1:
请同学制作两个全等的三角形。
想一想:
观察两个全等的三角形,将它们相等的一组边重合,得到一个怎样的四边形?对边有什么特征?
A
B
C
D
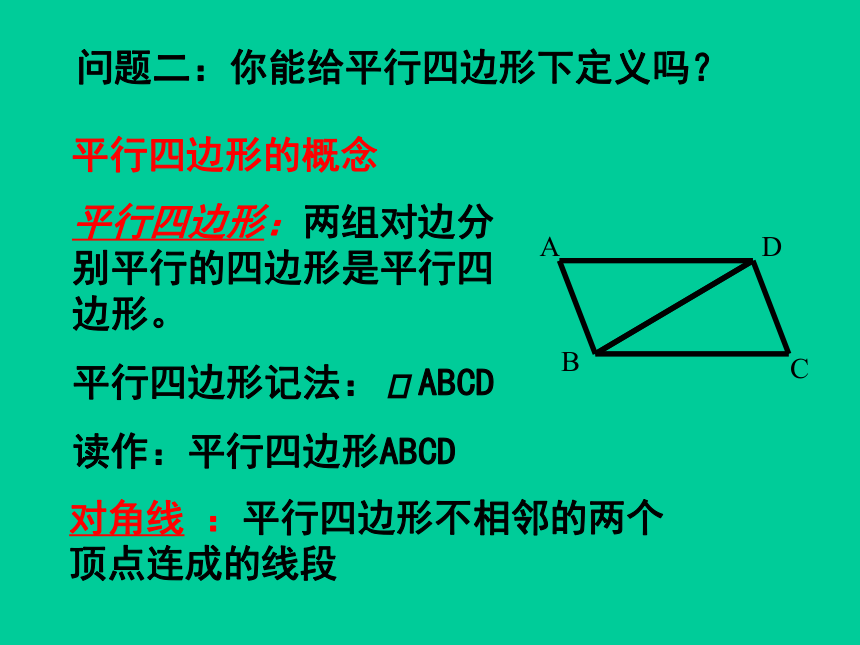
问题二:你能给平行四边形下定义吗?
对角线 :平行四边形不相邻的两个
顶点连成的线段
平行四边形的概念
平行四边形:两组对边分别平行的四边形是平行四边形。
平行四边形记法: ABCD
读作:平行四边形ABCD
D
C
B
A
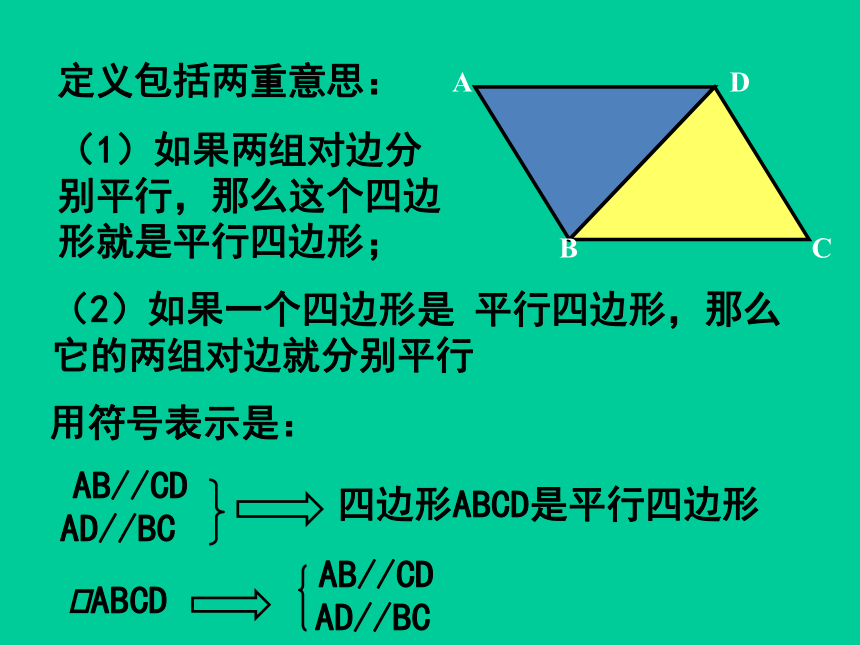
定义包括两重意思:
(1)如果两组对边分别平行,那么这个四边形就是平行四边形;
(2)如果一个四边形是 平行四边形,那么它的两组对边就分别平行
用符号表示是:
AB//CD
AD//BC
四边形ABCD是平行四边形
AB//CD
AD//BC
ABCD
∵ ∠1=∠2
∴ AD∥BC
D
C
B
A
1
2
3
4
∵ ∠3=∠4
∴ AB∥DC
∴ 四边形ABCD是平行四边形
生活中常见到那些平行四边形的实例,你能举出几个吗
体验感知
D
A
B
C
A
B
C
D
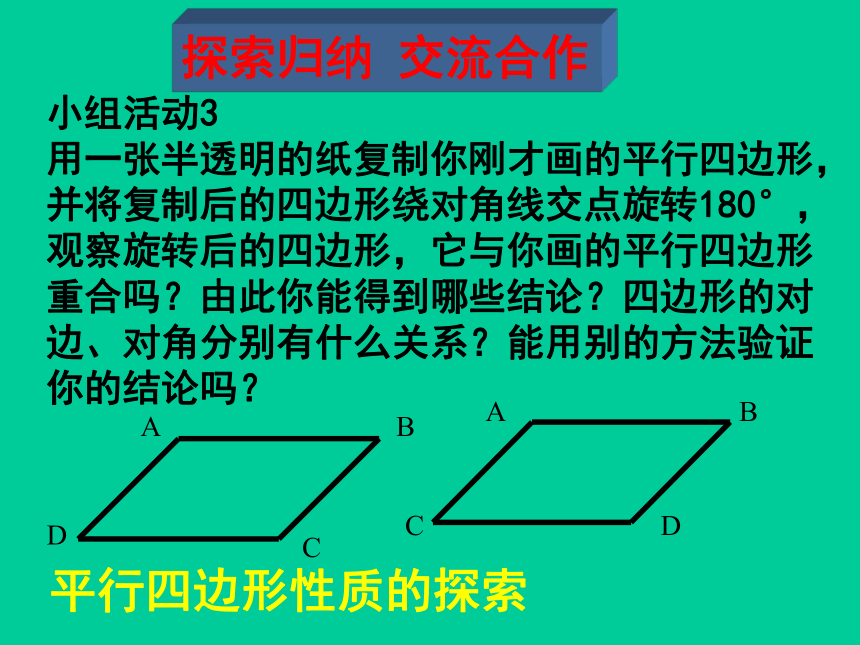
小组活动3
用一张半透明的纸复制你刚才画的平行四边形,并将复制后的四边形绕对角线交点旋转180°,观察旋转后的四边形,它与你画的平行四边形重合吗?由此你能得到哪些结论?四边形的对边、对角分别有什么关系?能用别的方法验证你的结论吗?
探索归纳 交流合作
平行四边形性质的探索
结论1:平行四边形是中心对称图形,
两条对角线的交点是他的对称中心
结论:
平行四边形的对边平行且相等。
平行四边形的对角相等。
∵ 四边形ABCD是平行四边形
∴ AB=DC , AD=BC.
∠A=∠C , ∠B=∠D.
∴ AB∥DC, AD∥BC
问题四:
平行四边形的对边、对角分别有 什么关系?
A
B
C
D
问题四:
平行四边形的性质:
平行四边形的对边相等
平行四边形的对角相等
能用别的方法验证你的结论吗?
推理论证 感悟升华
可以通过推理来证明这个结论:
例:如图6-2(1),四边形ABCD是平行四边形.
求证:AB=CD,BC=DA.
证明:如图6-2(2),连接AC.
∵ 四边形ABCD是平行四边形
∴ AD // BC,AB // CD
∴ ∠1=∠2,∠3=∠4
∴ △ABC和△CDA中
∠2=∠1
AC=CA
∠3=∠4
∴ △ABC≌△CDA(ASA)
∴ AB=DC, AD=CB
1
2
3
4
你能证明平行四边形的对角相等吗?
如图6-2(1),四边形ABCD是平行四边形.
求证: ∠A=∠C,∠B=∠D.
证明:如图6-2(2),连接AC.
∵ 四边形ABCD是平行四边形
∴ AD // BC, AB // CD
∴ ∠A+∠B=180 °
∠A+∠D=180 °
∴ ∠B=∠D
同理可得:∠A=∠C
1
2
3
4
应用巩固 深化提高
(1) 已知:如图6-3,在平行四边形ABCD中,
E,F 是对角线AC上的两点,且AE=CF.
求证:BE = DF.
证明:∵四边形ABCD是平行四边形
∴AB = CD
AB // CD
∴∠BAE=∠DCF
又∵AE=CF
∴△BAE≌△DCF
∴BE=DF
练一练:
A
B
C
D
(2)已知平行四边形一个内角的度数,能确
定其他三个内角的度数吗?说说你的理由。
应用巩固 深化提高
议一议:
经历了实践与探索,你有什么感受和收获
能给自己一个客观的评价吗 这节课你学
到了什么?
评价反思 概括总结
2.这节课与同伴合作交流中,你向同伴学到
了什么?
3.本节课在知识和方法对你有什么启发
考一考
1. ABCD中, ∠B=600,则∠A= ——, ∠C= ——, ∠D= ——.
2. ABCD中∠A比∠B大200,则∠C= ——.
ABCD中,AB=3cm,BC=5cm,
则AD= ——,CD= ——.
4.如果 ABCD的周长为40cm, ABC的周长为25cm,则对角线AC的长是( ).
A 5cm B 15cm C 6cm D 16cm
1200
1200
600
1000
5cm
3cm
A
平行四边形的性质2
回顾思考,引入新课
1.平行四边形都有哪些性质?
2.选一选:
(1)平行四边形ABCD中,∠A比∠B大20°,
则∠C的度数为( )
A.60° B.80° C.100° D.120°
(2)平行四边形ABCD的周长为40cm,△ABC的
周长为25cm, 则对角线AC长为( )
A.5cm B.15cm C.6cm D.16cm
对边平行且相等,对角相等,对角线互相平分
C
A
探索发现,灵活运用
在上节课的做一做中,我们发现平行四边形除了边、角有特殊的关系以外,对角线还有怎样的特殊关系呢?
结论:平行四边形的对角线互相平分.
探索发现,理性证明
已知:如图6-4,平行四边形ABCD的对角线AC、
BD相交于点O.
求证:OA=OC,OB=OD.
证明:∵ 四边形ABCD是平行四边形
∴ AB=CD AB//DC
∴ ∠BAO=∠DCO ∠ABO=∠CDO
∴ △AOB≌△COD
∴ OA=OC,OB=OD.
例1.如图6-5,在平行四边形ABCD中,点O是
对角线AC、BD的交点,过点O的直线分别与
AD、BC交于点E、F.
求证:OE=OF.
证明:
∵ 四边形ABCD是平行四边形
∴ AD=CB AD//BC OA=OC
∴ ∠DAC=∠ACB
又∵ ∠AOE=∠COF
∴ △AOE≌△COF
∴ OE=OF
探索发现,灵活运用
2.如图6-6, 平行四边形ABCD的对角线AC、BD
相交于点O, ∠ADB=900,OA=6,0B=3.
求AD和AC的长度.
解: ∵ 四边形ABCD是平行四边形
∴ OA=OC=6 OB=OD=3
∴ AC=12
又∵ ∠ADB=900
∴ 在Rt△ADO中,
根据勾股定理得:OA2=0D2+AD2
∴ AD=3
探索发现,灵活运用
观察分析,理性升华
已知,如图,在平行四边形ABCD中,平行于对
角线AC的直线MN分别交DA,DC的延长线于M,N,
交BA,BC于点P,点B,你能说明MQ=NP吗?
解:∵四边形ABCD是平行四边形
∴AD//BC,AB//CD 即AM//CQ
又∵AC//MN 即AC//MQ
∴四边形MQCA是平行四边形
∴MQ=AC
同理 NP=AC
∴MQ=NP
巩固反馈,总结提高
1.在平行四边形ABCD中,∠A=150°,AB=8cm,
BC=10cm,求平行四边形ABCD的面积。
解:过A作AE⊥BC交BC于E,
∵四边形ABCD是平行四边形
∴AD//BC
∴∠BAD+∠B =180°
∵∠BAD =150°
∴∠B =30°
在Rt△ABE中,∠B =30°
∴AE =1/2AB=4
∴平行四边形ABCD的面积=4×10=40cm2
巩固反馈,总结提高
2.平行四边形ABCD的两条对角线相交于O,OA,
OB,AB的长度分别为3cm、4cm、5cm,
求其它各边以及两条对角线的长度。
解:∵四边形ABCD是平行四边形
∴AB=CD,AD=BC
OA=OC,OB=OD
又∵OA=3cm, OB=4cm, AB=5cm
∴AC=6cm BD=8cm CD=5cm
∵△AOB中,32+42=52,即AO2+BO2=AB2
∴∠AOB =90°
∴AC⊥BD
∴Rt△AOD中,OA2+OD2=AD2
∴AD=5cm,BC=5cm.
评价反思,目标回顾
1.本节课你有哪些收获?
你能将平行四边形的性质进行归纳吗?
2.利用平行四边形可以解决哪些问题?
3.你能给自己和同伴本节课一个评价吗?
平行四边形的性质1
平行四边形特征的探索
做一做 :小组活动1:
请同学制作两个全等的三角形。
想一想:
观察两个全等的三角形,将它们相等的一组边重合,得到一个怎样的四边形?对边有什么特征?
A
B
C
D
问题二:你能给平行四边形下定义吗?
对角线 :平行四边形不相邻的两个
顶点连成的线段
平行四边形的概念
平行四边形:两组对边分别平行的四边形是平行四边形。
平行四边形记法: ABCD
读作:平行四边形ABCD
D
C
B
A
定义包括两重意思:
(1)如果两组对边分别平行,那么这个四边形就是平行四边形;
(2)如果一个四边形是 平行四边形,那么它的两组对边就分别平行
用符号表示是:
AB//CD
AD//BC
四边形ABCD是平行四边形
AB//CD
AD//BC
ABCD
∵ ∠1=∠2
∴ AD∥BC
D
C
B
A
1
2
3
4
∵ ∠3=∠4
∴ AB∥DC
∴ 四边形ABCD是平行四边形
生活中常见到那些平行四边形的实例,你能举出几个吗
体验感知
D
A
B
C
A
B
C
D
小组活动3
用一张半透明的纸复制你刚才画的平行四边形,并将复制后的四边形绕对角线交点旋转180°,观察旋转后的四边形,它与你画的平行四边形重合吗?由此你能得到哪些结论?四边形的对边、对角分别有什么关系?能用别的方法验证你的结论吗?
探索归纳 交流合作
平行四边形性质的探索
结论1:平行四边形是中心对称图形,
两条对角线的交点是他的对称中心
结论:
平行四边形的对边平行且相等。
平行四边形的对角相等。
∵ 四边形ABCD是平行四边形
∴ AB=DC , AD=BC.
∠A=∠C , ∠B=∠D.
∴ AB∥DC, AD∥BC
问题四:
平行四边形的对边、对角分别有 什么关系?
A
B
C
D
问题四:
平行四边形的性质:
平行四边形的对边相等
平行四边形的对角相等
能用别的方法验证你的结论吗?
推理论证 感悟升华
可以通过推理来证明这个结论:
例:如图6-2(1),四边形ABCD是平行四边形.
求证:AB=CD,BC=DA.
证明:如图6-2(2),连接AC.
∵ 四边形ABCD是平行四边形
∴ AD // BC,AB // CD
∴ ∠1=∠2,∠3=∠4
∴ △ABC和△CDA中
∠2=∠1
AC=CA
∠3=∠4
∴ △ABC≌△CDA(ASA)
∴ AB=DC, AD=CB
1
2
3
4
你能证明平行四边形的对角相等吗?
如图6-2(1),四边形ABCD是平行四边形.
求证: ∠A=∠C,∠B=∠D.
证明:如图6-2(2),连接AC.
∵ 四边形ABCD是平行四边形
∴ AD // BC, AB // CD
∴ ∠A+∠B=180 °
∠A+∠D=180 °
∴ ∠B=∠D
同理可得:∠A=∠C
1
2
3
4
应用巩固 深化提高
(1) 已知:如图6-3,在平行四边形ABCD中,
E,F 是对角线AC上的两点,且AE=CF.
求证:BE = DF.
证明:∵四边形ABCD是平行四边形
∴AB = CD
AB // CD
∴∠BAE=∠DCF
又∵AE=CF
∴△BAE≌△DCF
∴BE=DF
练一练:
A
B
C
D
(2)已知平行四边形一个内角的度数,能确
定其他三个内角的度数吗?说说你的理由。
应用巩固 深化提高
议一议:
经历了实践与探索,你有什么感受和收获
能给自己一个客观的评价吗 这节课你学
到了什么?
评价反思 概括总结
2.这节课与同伴合作交流中,你向同伴学到
了什么?
3.本节课在知识和方法对你有什么启发
考一考
1. ABCD中, ∠B=600,则∠A= ——, ∠C= ——, ∠D= ——.
2. ABCD中∠A比∠B大200,则∠C= ——.
ABCD中,AB=3cm,BC=5cm,
则AD= ——,CD= ——.
4.如果 ABCD的周长为40cm, ABC的周长为25cm,则对角线AC的长是( ).
A 5cm B 15cm C 6cm D 16cm
1200
1200
600
1000
5cm
3cm
A
平行四边形的性质2
回顾思考,引入新课
1.平行四边形都有哪些性质?
2.选一选:
(1)平行四边形ABCD中,∠A比∠B大20°,
则∠C的度数为( )
A.60° B.80° C.100° D.120°
(2)平行四边形ABCD的周长为40cm,△ABC的
周长为25cm, 则对角线AC长为( )
A.5cm B.15cm C.6cm D.16cm
对边平行且相等,对角相等,对角线互相平分
C
A
探索发现,灵活运用
在上节课的做一做中,我们发现平行四边形除了边、角有特殊的关系以外,对角线还有怎样的特殊关系呢?
结论:平行四边形的对角线互相平分.
探索发现,理性证明
已知:如图6-4,平行四边形ABCD的对角线AC、
BD相交于点O.
求证:OA=OC,OB=OD.
证明:∵ 四边形ABCD是平行四边形
∴ AB=CD AB//DC
∴ ∠BAO=∠DCO ∠ABO=∠CDO
∴ △AOB≌△COD
∴ OA=OC,OB=OD.
例1.如图6-5,在平行四边形ABCD中,点O是
对角线AC、BD的交点,过点O的直线分别与
AD、BC交于点E、F.
求证:OE=OF.
证明:
∵ 四边形ABCD是平行四边形
∴ AD=CB AD//BC OA=OC
∴ ∠DAC=∠ACB
又∵ ∠AOE=∠COF
∴ △AOE≌△COF
∴ OE=OF
探索发现,灵活运用
2.如图6-6, 平行四边形ABCD的对角线AC、BD
相交于点O, ∠ADB=900,OA=6,0B=3.
求AD和AC的长度.
解: ∵ 四边形ABCD是平行四边形
∴ OA=OC=6 OB=OD=3
∴ AC=12
又∵ ∠ADB=900
∴ 在Rt△ADO中,
根据勾股定理得:OA2=0D2+AD2
∴ AD=3
探索发现,灵活运用
观察分析,理性升华
已知,如图,在平行四边形ABCD中,平行于对
角线AC的直线MN分别交DA,DC的延长线于M,N,
交BA,BC于点P,点B,你能说明MQ=NP吗?
解:∵四边形ABCD是平行四边形
∴AD//BC,AB//CD 即AM//CQ
又∵AC//MN 即AC//MQ
∴四边形MQCA是平行四边形
∴MQ=AC
同理 NP=AC
∴MQ=NP
巩固反馈,总结提高
1.在平行四边形ABCD中,∠A=150°,AB=8cm,
BC=10cm,求平行四边形ABCD的面积。
解:过A作AE⊥BC交BC于E,
∵四边形ABCD是平行四边形
∴AD//BC
∴∠BAD+∠B =180°
∵∠BAD =150°
∴∠B =30°
在Rt△ABE中,∠B =30°
∴AE =1/2AB=4
∴平行四边形ABCD的面积=4×10=40cm2
巩固反馈,总结提高
2.平行四边形ABCD的两条对角线相交于O,OA,
OB,AB的长度分别为3cm、4cm、5cm,
求其它各边以及两条对角线的长度。
解:∵四边形ABCD是平行四边形
∴AB=CD,AD=BC
OA=OC,OB=OD
又∵OA=3cm, OB=4cm, AB=5cm
∴AC=6cm BD=8cm CD=5cm
∵△AOB中,32+42=52,即AO2+BO2=AB2
∴∠AOB =90°
∴AC⊥BD
∴Rt△AOD中,OA2+OD2=AD2
∴AD=5cm,BC=5cm.
评价反思,目标回顾
1.本节课你有哪些收获?
你能将平行四边形的性质进行归纳吗?
2.利用平行四边形可以解决哪些问题?
3.你能给自己和同伴本节课一个评价吗?
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
