北师大版八年级数学下册 6.1 平行四边形的边和角的性质 课件(共19张PPT)
文档属性
| 名称 | 北师大版八年级数学下册 6.1 平行四边形的边和角的性质 课件(共19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-19 16:01:09 | ||
图片预览




文档简介
(共19张PPT)
§ 6.1 .1平行四边形的性质
北师版八下第六章
找一找
(一)探索新知
找一找
(一)探索新知
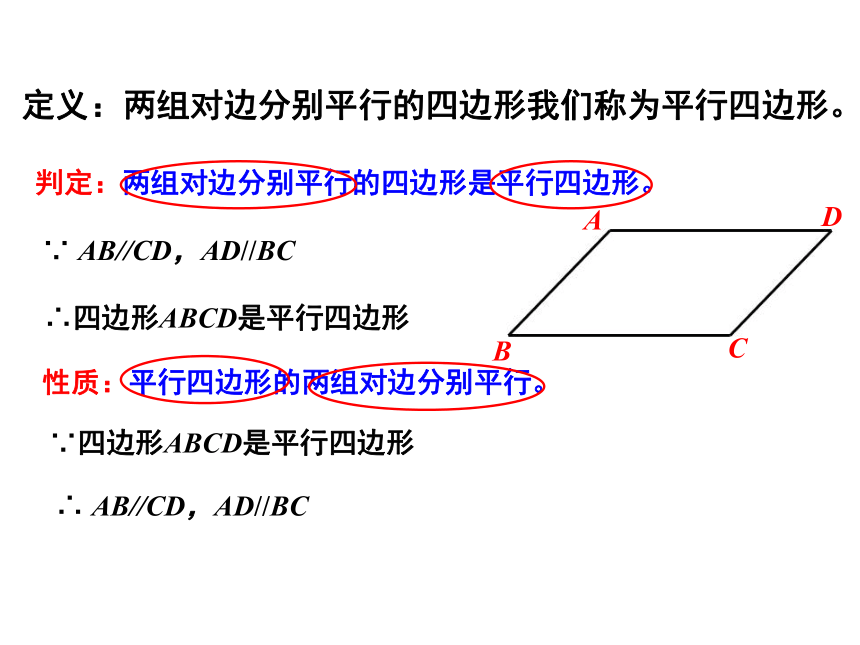
定义:两组对边分别平行的四边形我们称为平行四边形。
读作“平行四边形ABCD”
AB与CD,AD与BC
∠A与∠C,∠B与∠D
AC,BD
记作“ ”
如图,
对边:
对角:
对角线:
(一)探索新知
O
A
B
C
D
定义:两组对边分别平行的四边形我们称为平行四边形。
∴四边形ABCD是平行四边形
∵ AB//CD,AD//BC
判定:两组对边分别平行的四边形是平行四边形。
性质:平行四边形的两组对边分别平行。
(一)探索新知
∵四边形ABCD是平行四边形
∴ AB//CD,AD//BC
A
C
D
B
问:类比研究等腰三角形的方法,我们可以从哪几个方面研究
平行四边形性质?
(二)动手操作
边、角、对角线
活动1:打开你们的思路,大胆地猜想平行四边形的性质。
小组合作,拿出你们准备好的工具(直尺、三角尺、量角器、卡纸等),选择适当的方法猜想你们的结论。
(1)你们小组选择的方法:
①度量 ②平移 ③旋转 ④平移、旋转
⑤折叠 ⑥拼图 ⑦其它
(2)你们发现的结论: 。
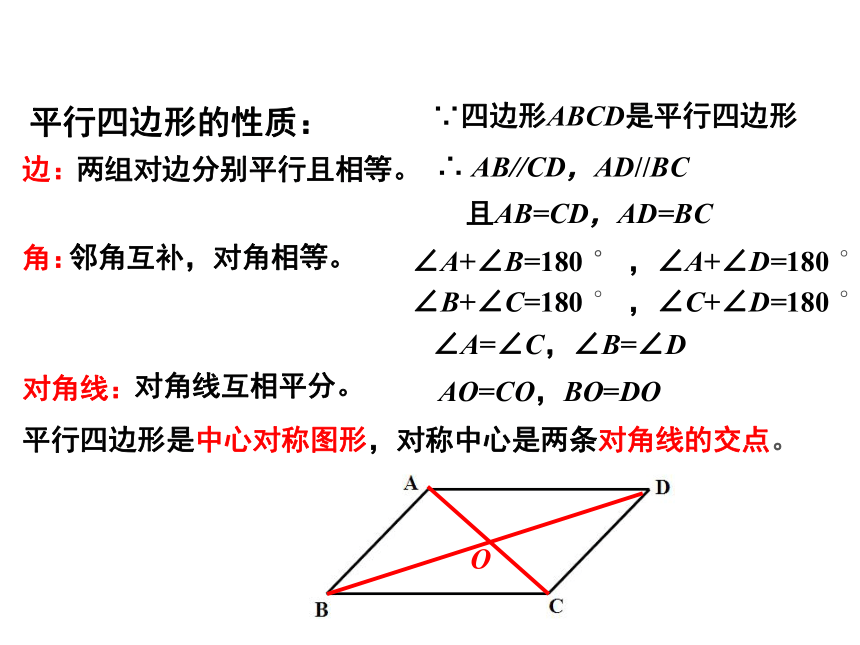
平行四边形的性质:
(三)猜想归纳
边:
角:
对角线:
O
平行四边形是中心对称图形,对称中心是两条对角线的交点。
∵四边形ABCD是平行四边形
∴ AB//CD,AD//BC
∠A=∠C,∠B=∠D
AO=CO,BO=DO
且AB=CD,AD=BC
两组对边分别平行且相等。
邻角互补,对角相等。
对角线互相平分。
∠A+∠B=180 ° ,∠A+∠D=180 °
∠B+∠C=180 ° ,∠C+∠D=180 °
1 .平行四边形的两组对边分别相等。
2 .平行四边形的两组对角分别相等。
(四)推理验证
活动2:
问:命题证明有哪些步骤?
1、画图
2、写已知、求证
3、证明
(五)学以致用
活动3:
1 . 给你两张一组对边平行的纸条(如图7),怎样操作,
可以构成一个平行四边形?请同学们动手试试,并说
明理由。
(五)学以致用
活动3:
2 .如图10,每个小正方形的边长为1,以AB为一边,画一个
周长为18的平行四边形ABCD(要求平行四边形的顶点在
格点上)。 并说明你画的理由。
∵AB//CD,AD//BC
∴四边形ABCD是平行四边形
连结AC,
∵AB=CD=4,BC=AD=5,AC=AC
∴△ACD≌△CAB
∴∠DAC=∠BCA
∴AD//BC
又∵AB//CD
∴四边形ABCD是平行四边形
如果所画的平行四边形的顶点不要求在格点上,这样的平行四边形可以画几个?
平行四边形的不稳定性
(五)学以致用
活动3:
3.已知,如图,在 中,E,F是对角线AC上的两点,
并且AE=CF。
求证:BE=DF。
(六)课堂小结
本节学习到了什么?
(1)本节课我们主要学习什么数学知识?
(2)我们是从哪几个方面探究平行四边形的性质?
(3)平行四边形的性质的有哪些?
(七)布置作业
1、课本P137,习题6.1,第1,2,3,4题
2、优化P53-54,<平行四边形的性质>第1课时
§ 6.1 .1平行四边形的性质
北师版八下第六章
找一找
(一)探索新知
找一找
(一)探索新知
定义:两组对边分别平行的四边形我们称为平行四边形。
读作“平行四边形ABCD”
AB与CD,AD与BC
∠A与∠C,∠B与∠D
AC,BD
记作“ ”
如图,
对边:
对角:
对角线:
(一)探索新知
O
A
B
C
D
定义:两组对边分别平行的四边形我们称为平行四边形。
∴四边形ABCD是平行四边形
∵ AB//CD,AD//BC
判定:两组对边分别平行的四边形是平行四边形。
性质:平行四边形的两组对边分别平行。
(一)探索新知
∵四边形ABCD是平行四边形
∴ AB//CD,AD//BC
A
C
D
B
问:类比研究等腰三角形的方法,我们可以从哪几个方面研究
平行四边形性质?
(二)动手操作
边、角、对角线
活动1:打开你们的思路,大胆地猜想平行四边形的性质。
小组合作,拿出你们准备好的工具(直尺、三角尺、量角器、卡纸等),选择适当的方法猜想你们的结论。
(1)你们小组选择的方法:
①度量 ②平移 ③旋转 ④平移、旋转
⑤折叠 ⑥拼图 ⑦其它
(2)你们发现的结论: 。
平行四边形的性质:
(三)猜想归纳
边:
角:
对角线:
O
平行四边形是中心对称图形,对称中心是两条对角线的交点。
∵四边形ABCD是平行四边形
∴ AB//CD,AD//BC
∠A=∠C,∠B=∠D
AO=CO,BO=DO
且AB=CD,AD=BC
两组对边分别平行且相等。
邻角互补,对角相等。
对角线互相平分。
∠A+∠B=180 ° ,∠A+∠D=180 °
∠B+∠C=180 ° ,∠C+∠D=180 °
1 .平行四边形的两组对边分别相等。
2 .平行四边形的两组对角分别相等。
(四)推理验证
活动2:
问:命题证明有哪些步骤?
1、画图
2、写已知、求证
3、证明
(五)学以致用
活动3:
1 . 给你两张一组对边平行的纸条(如图7),怎样操作,
可以构成一个平行四边形?请同学们动手试试,并说
明理由。
(五)学以致用
活动3:
2 .如图10,每个小正方形的边长为1,以AB为一边,画一个
周长为18的平行四边形ABCD(要求平行四边形的顶点在
格点上)。 并说明你画的理由。
∵AB//CD,AD//BC
∴四边形ABCD是平行四边形
连结AC,
∵AB=CD=4,BC=AD=5,AC=AC
∴△ACD≌△CAB
∴∠DAC=∠BCA
∴AD//BC
又∵AB//CD
∴四边形ABCD是平行四边形
如果所画的平行四边形的顶点不要求在格点上,这样的平行四边形可以画几个?
平行四边形的不稳定性
(五)学以致用
活动3:
3.已知,如图,在 中,E,F是对角线AC上的两点,
并且AE=CF。
求证:BE=DF。
(六)课堂小结
本节学习到了什么?
(1)本节课我们主要学习什么数学知识?
(2)我们是从哪几个方面探究平行四边形的性质?
(3)平行四边形的性质的有哪些?
(七)布置作业
1、课本P137,习题6.1,第1,2,3,4题
2、优化P53-54,<平行四边形的性质>第1课时
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
