人教版七年级数学上册1 .2.2数轴 教学设计(表格式)
文档属性
| 名称 | 人教版七年级数学上册1 .2.2数轴 教学设计(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-19 00:00:00 | ||
图片预览

文档简介
1.2.2 数轴教学设计
〖教学内容解析〗
“数轴”,是人教版七年级数学上册第一章第二节“有理数”的重点内容之一,是在引进了负数及分析了有理数的分类后给出的。数轴是理解有理数的概念与运算的重要工具,利用这个数学工具不但可以理解有理数的概念、大小比较等,还可以利用它来解决一些实际问题,包括相反数、绝对值、有理数的运算等,非常直观地建立了实数(有理数与无理数)与数轴上的点一一对应的关系,闪烁着“数形结合”的数学思想光芒;展现出数学概念学习的一个完整的学习范式,对以后的数学学习起着示范的作用.
〖教学目标〗
知识技能目标:
(1)掌握数轴的概念,并理解其三要素,能正确地画出数轴;
能将有理数用数轴上的点表示出来;知道“所有的有理数,都可以用数轴上的点表示”.
(3)能够将数轴上表示有理数的点说出它所表示的有理数;知道“数轴上的点除了表示有理数之外还有表示其他数的点”.
数学思考
(1)通过对数轴的学习,初步体会对应的思想、数形结合的思想.
(2)初步体会数学概念学习的基本范式.
解决问题
通过数轴概念的形成与发生过程,初步体验从数学的角度发现问题和提出问题;通过“议一议”的数学活动,初步体会合作学习,学习与他人合作交流;会利用数轴解决有关问题.
情感态度目标:
通过“自学课文”、“讨论归纳”、“例题讲解”、“当堂训练”和“总结提升”五个教学环节的实施,向学生渗透数形结合的数学思想,让学生知道数学来源于生活实践,培育学生对数学的学习兴趣、培养学生的反思质疑等学习习惯.
〖学情分析〗
学生在小学已经学习了整数、分数,对负数的意义也有了初步的了解,通过前一节课的学习把数扩充到了有理数,他们能够用正数、负数来表示一些相反意义的量.
教学重点:数轴的概念,会用数轴上的点表示有理数;
教学难点:从直观认识到理性认识,建立数轴的概念,正确画出数轴。
【关于教学过程的安排】
教学 程 序 教 与 学 的 活 动 设计的意图
课 前 自 学 教师指导学生自学课文,解决问题: 1、什么叫数轴?它有什么作用? 2、数轴的特征是什么
3、教材P3练习1、2题。 通过老师指导,让学生在自学中掌握知识的同时,提升自我学习能力
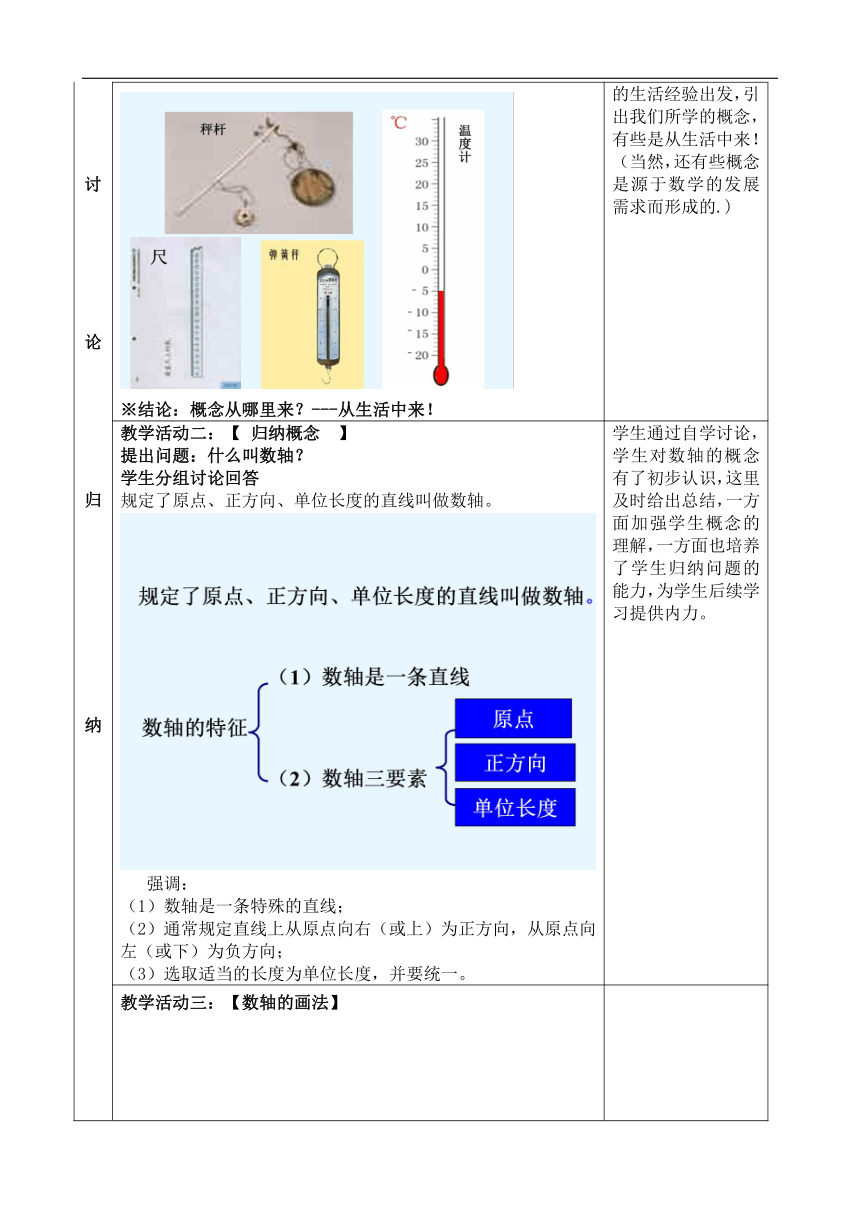
讨 论 归 纳 概念从哪里来? 教学活动一:【生活中用直线上的点表示数的例子】 ※结论:概念从哪里来?---从生活中来! 概念从生活中来.数学源于生活,又服务于生活。从学生已有的生活经验出发,引出我们所学的概念,有些是从生活中来!(当然,还有些概念是源于数学的发展需求而形成的.)
教学活动二:【 归纳概念 】 提出问题:什么叫数轴? 学生分组讨论回答 规定了原点、正方向、单位长度的直线叫做数轴。 强调:
(1)数轴是一条特殊的直线;
(2)通常规定直线上从原点向右(或上)为正方向,从原点向左(或下)为负方向; (3)选取适当的长度为单位长度,并要统一。
学生通过自学讨论,学生对数轴的概念有了初步认识,这里及时给出总结,一方面加强学生概念的理解,一方面也培养了学生归纳问题的能力,为学生后续学习提供内力。
教学活动三:【数轴的画法】 议一议:怎样画数轴? ① 画直线,定原点。
② 确定正方向,并用箭头表示。 ③ 选取适当长度为单位长度,并统一。 ④ 在数轴上标出1,2,3,-1,-2,-3等各点。 画说情境.通过学生的活动(辨识、讨论、总结),体会数轴的画法以及画数轴时容易出现的问题,给他们以较深印象。
教学活动四:【火眼金睛】 在学生对数轴有了一定认识后再次提出对画数轴中出现问题进行辨识,加强学生印象,突破难点。
例 题 讲 解 概念怎么用? 教学活动一:【 在数轴上表示下列各数】 例1:在所给数轴上画出表示下列各数的点。
1,-5,-2.5, 4, 0
教学活动二:【数轴上的点表示的数】 例2 指出数轴上A、B、C、D、E、F各点分别表示什么数
在数轴上表示数.通过在数轴上表示有理数的体验,让学生知道“所有的有理数都可以用数轴上的点来表示”.选取适当长度为单位长度对于“问题解决”的必要性.. 数轴上的点表示的数. 通过描述数轴上的点分别表示什么数以及实物演示圆滚动一周经过的路径长度,学生认识到数轴上除了有表示有理数的点以外,还有象π一样的数.
教学活动三:【感悟数学思想】 观察例题的数轴回答问题:
哪些数在原点的左边,哪些数在原点的右边,每个数到原点的距离是多少?由此你发现了什么规律? 归纳:
(1)任何有理数都可以用数轴上的点来表示,但数轴上的点并不都表示有理数。
(2)数轴上表示正数的点在原点的 边,表示负数的点在原点的 边。 (3)数轴上右边的点表示的数总比左边的大。 感悟数学思想 .回味“在数轴上表示数”和“数轴上的点表示的数”两个教学活动;感悟“抽象的数与直观的形结合在一起”的数学事实,帮助学生初步感知数形结合思想.
教学活动四:【感悟数学学习】 回味“在数轴上表示数”和“数轴上的点表示的数”两个教学活动;体会:有理数(还有无理数)可以用数轴上的点表示,数轴上的点表示的数既有理数还有无理数(以后我们将学到). 抽象的数(有理数和无理数)和直观的点(直线上的点)建立了一一对应的关系(这里的“一一对应”在以后的学习中同学们会理解它的含义的.) 数与点的对应关系,这可是一种重要的数学思想——数形结合思想 . 感悟数学学习.体会“概念学习”的基本范式,让学生在学到知识的同时,学会学习.
梳 理 反 思 教学活动一: 今天我们学了什么? 教学活动二: 今天我们悟到什么? 教学活动三: 今天的质疑和发现? 学了什么是梳理;悟到什么是思考;质疑与发现是学会发现问题和提出问题.
巩 固 放 飞 【布置作业】 1.巩固性作业:课本P14 第2、3题 (必做) 2.拓展性作业 :数轴上表示整数的点称为整点,某数轴的单位长度是1cm,若在这个数轴上任意画一条长为2015cm的线段AB,则线段AB盖住的整点个数有________个 (希望大家都做) 3.研究性作业:数轴是数与形的第一次碰撞 ,请收集有关数形结合思想的资料。 (小组合作完成) 巩固性作业帮助学生巩固所学内容;.拓展性作业帮助学生“跳起来学”;研究性作业帮助学生学会合作、学会学习. 上帝忘了给我们翅膀,我们只好用思维来飞翔;热爱阅读吧!读书,将会给你插上思考的翅膀.
〖教学内容解析〗
“数轴”,是人教版七年级数学上册第一章第二节“有理数”的重点内容之一,是在引进了负数及分析了有理数的分类后给出的。数轴是理解有理数的概念与运算的重要工具,利用这个数学工具不但可以理解有理数的概念、大小比较等,还可以利用它来解决一些实际问题,包括相反数、绝对值、有理数的运算等,非常直观地建立了实数(有理数与无理数)与数轴上的点一一对应的关系,闪烁着“数形结合”的数学思想光芒;展现出数学概念学习的一个完整的学习范式,对以后的数学学习起着示范的作用.
〖教学目标〗
知识技能目标:
(1)掌握数轴的概念,并理解其三要素,能正确地画出数轴;
能将有理数用数轴上的点表示出来;知道“所有的有理数,都可以用数轴上的点表示”.
(3)能够将数轴上表示有理数的点说出它所表示的有理数;知道“数轴上的点除了表示有理数之外还有表示其他数的点”.
数学思考
(1)通过对数轴的学习,初步体会对应的思想、数形结合的思想.
(2)初步体会数学概念学习的基本范式.
解决问题
通过数轴概念的形成与发生过程,初步体验从数学的角度发现问题和提出问题;通过“议一议”的数学活动,初步体会合作学习,学习与他人合作交流;会利用数轴解决有关问题.
情感态度目标:
通过“自学课文”、“讨论归纳”、“例题讲解”、“当堂训练”和“总结提升”五个教学环节的实施,向学生渗透数形结合的数学思想,让学生知道数学来源于生活实践,培育学生对数学的学习兴趣、培养学生的反思质疑等学习习惯.
〖学情分析〗
学生在小学已经学习了整数、分数,对负数的意义也有了初步的了解,通过前一节课的学习把数扩充到了有理数,他们能够用正数、负数来表示一些相反意义的量.
教学重点:数轴的概念,会用数轴上的点表示有理数;
教学难点:从直观认识到理性认识,建立数轴的概念,正确画出数轴。
【关于教学过程的安排】
教学 程 序 教 与 学 的 活 动 设计的意图
课 前 自 学 教师指导学生自学课文,解决问题: 1、什么叫数轴?它有什么作用? 2、数轴的特征是什么
3、教材P3练习1、2题。 通过老师指导,让学生在自学中掌握知识的同时,提升自我学习能力
讨 论 归 纳 概念从哪里来? 教学活动一:【生活中用直线上的点表示数的例子】 ※结论:概念从哪里来?---从生活中来! 概念从生活中来.数学源于生活,又服务于生活。从学生已有的生活经验出发,引出我们所学的概念,有些是从生活中来!(当然,还有些概念是源于数学的发展需求而形成的.)
教学活动二:【 归纳概念 】 提出问题:什么叫数轴? 学生分组讨论回答 规定了原点、正方向、单位长度的直线叫做数轴。 强调:
(1)数轴是一条特殊的直线;
(2)通常规定直线上从原点向右(或上)为正方向,从原点向左(或下)为负方向; (3)选取适当的长度为单位长度,并要统一。
学生通过自学讨论,学生对数轴的概念有了初步认识,这里及时给出总结,一方面加强学生概念的理解,一方面也培养了学生归纳问题的能力,为学生后续学习提供内力。
教学活动三:【数轴的画法】 议一议:怎样画数轴? ① 画直线,定原点。
② 确定正方向,并用箭头表示。 ③ 选取适当长度为单位长度,并统一。 ④ 在数轴上标出1,2,3,-1,-2,-3等各点。 画说情境.通过学生的活动(辨识、讨论、总结),体会数轴的画法以及画数轴时容易出现的问题,给他们以较深印象。
教学活动四:【火眼金睛】 在学生对数轴有了一定认识后再次提出对画数轴中出现问题进行辨识,加强学生印象,突破难点。
例 题 讲 解 概念怎么用? 教学活动一:【 在数轴上表示下列各数】 例1:在所给数轴上画出表示下列各数的点。
1,-5,-2.5, 4, 0
教学活动二:【数轴上的点表示的数】 例2 指出数轴上A、B、C、D、E、F各点分别表示什么数
在数轴上表示数.通过在数轴上表示有理数的体验,让学生知道“所有的有理数都可以用数轴上的点来表示”.选取适当长度为单位长度对于“问题解决”的必要性.. 数轴上的点表示的数. 通过描述数轴上的点分别表示什么数以及实物演示圆滚动一周经过的路径长度,学生认识到数轴上除了有表示有理数的点以外,还有象π一样的数.
教学活动三:【感悟数学思想】 观察例题的数轴回答问题:
哪些数在原点的左边,哪些数在原点的右边,每个数到原点的距离是多少?由此你发现了什么规律? 归纳:
(1)任何有理数都可以用数轴上的点来表示,但数轴上的点并不都表示有理数。
(2)数轴上表示正数的点在原点的 边,表示负数的点在原点的 边。 (3)数轴上右边的点表示的数总比左边的大。 感悟数学思想 .回味“在数轴上表示数”和“数轴上的点表示的数”两个教学活动;感悟“抽象的数与直观的形结合在一起”的数学事实,帮助学生初步感知数形结合思想.
教学活动四:【感悟数学学习】 回味“在数轴上表示数”和“数轴上的点表示的数”两个教学活动;体会:有理数(还有无理数)可以用数轴上的点表示,数轴上的点表示的数既有理数还有无理数(以后我们将学到). 抽象的数(有理数和无理数)和直观的点(直线上的点)建立了一一对应的关系(这里的“一一对应”在以后的学习中同学们会理解它的含义的.) 数与点的对应关系,这可是一种重要的数学思想——数形结合思想 . 感悟数学学习.体会“概念学习”的基本范式,让学生在学到知识的同时,学会学习.
梳 理 反 思 教学活动一: 今天我们学了什么? 教学活动二: 今天我们悟到什么? 教学活动三: 今天的质疑和发现? 学了什么是梳理;悟到什么是思考;质疑与发现是学会发现问题和提出问题.
巩 固 放 飞 【布置作业】 1.巩固性作业:课本P14 第2、3题 (必做) 2.拓展性作业 :数轴上表示整数的点称为整点,某数轴的单位长度是1cm,若在这个数轴上任意画一条长为2015cm的线段AB,则线段AB盖住的整点个数有________个 (希望大家都做) 3.研究性作业:数轴是数与形的第一次碰撞 ,请收集有关数形结合思想的资料。 (小组合作完成) 巩固性作业帮助学生巩固所学内容;.拓展性作业帮助学生“跳起来学”;研究性作业帮助学生学会合作、学会学习. 上帝忘了给我们翅膀,我们只好用思维来飞翔;热爱阅读吧!读书,将会给你插上思考的翅膀.
