人教版七年级数学上册4.3.3 余角与补角(1)教学设计
文档属性
| 名称 | 人教版七年级数学上册4.3.3 余角与补角(1)教学设计 |

|
|
| 格式 | doc | ||
| 文件大小 | 83.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-19 00:00:00 | ||
图片预览

文档简介
§4.3.3 余角与补角(1)
教学目标:
1、知识与技能:
在具体的现实情境中,认识一个角的余角和补角,掌握余角和补角的性质及简单应用
2、过程与方法:
通过活动提高学生的抽象概括能力,发展空间观念和知识运用能力,学会简单的逻辑推理,并能对问题的结论进行合理的猜想。
3、情感态度与价值观:
体会观察、归纳、推理对数学知识中获取数学猜想和论证的重要作用,初步数学中推理的严谨性和结论的确定性,能在独立思考和小组交流中获益。
重、难点:
1、重点:认识角的互余、互补关系及其性质,是本节课的重点。
2、难点:通过简单的推理,归纳出余角、补角的性质,并能用规范的语言描述性质是难点。
一、引入新课:
1问题引入 :回顾平角、周角定义
2明确目标:a余角与补角概念b余角性质与补角性质C概念及性质的应用
二、新知探究
活动一
请同学们拿出三角板并观察三角板每个角的度数,分小组用三角板拼图,要求用三角板的两个锐角组成直角。
(让学生说出自己的方法:可以测量,也可以剪纸板拼等等,学生的方法只要合理就应鼓励)
教师活动:用多媒体演示
通过上面的演示,我们看到有时两个角的和是90°,也就是两个角之和正好成一直角,在这种情况下,我们给出互为余角概念
互为余角定义:如果两个锐角的和是一个直角90°,那么这两个角互为余角.简称互余.用数学式子表示为:因为∠1+∠2=90°,所以∠1与∠2互余.反之,因为∠1与∠2互余,所以∠1+∠2=90°
找朋友:图中给出的各角,那些互为余角?
教师活动:用多媒体演示
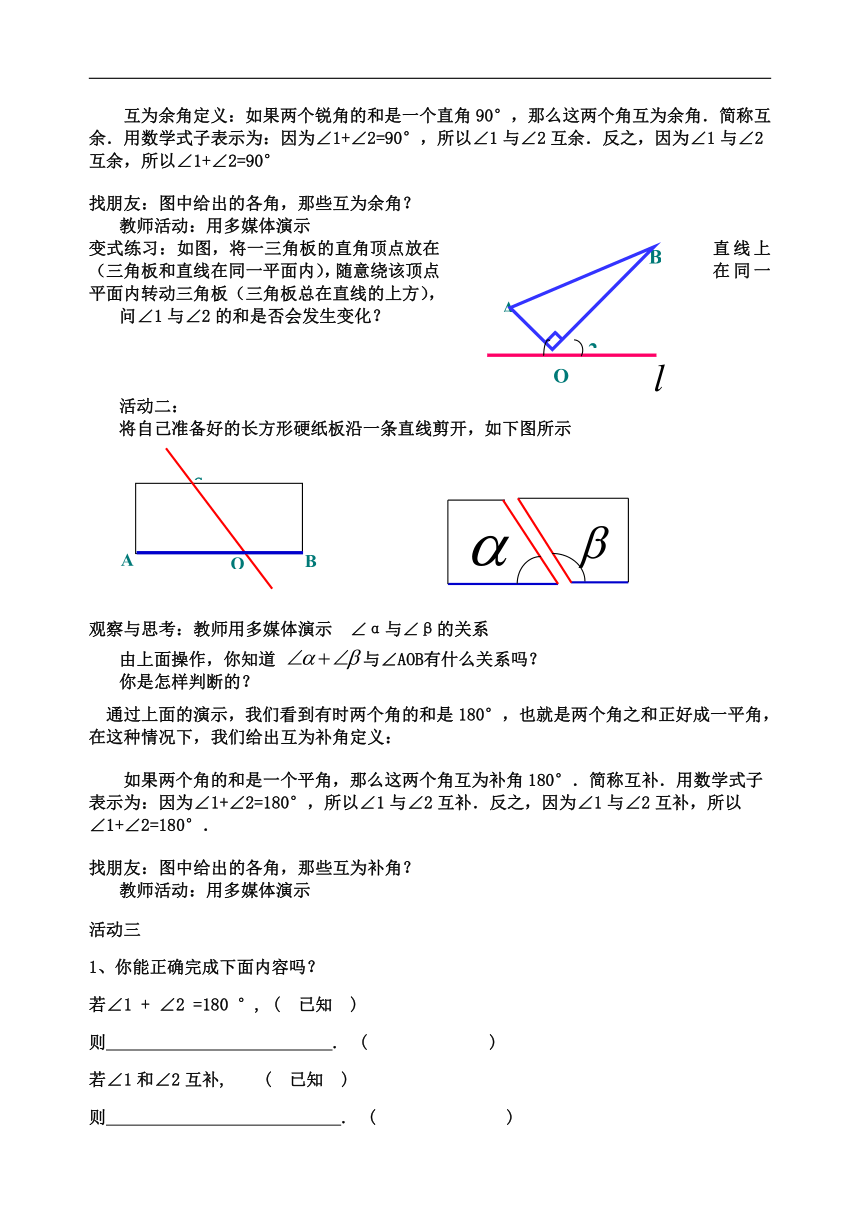
变式练习:如图,将一三角板的直角顶点放在直线上(三角板和直线在同一平面内),随意绕该顶点在同一平面内转动三角板(三角板总在直线的上方),
问∠1与∠2的和是否会发生变化?
活动二:
将自己准备好的长方形硬纸板沿一条直线剪开,如下图所示
观察与思考:教师用多媒体演示 ∠α与∠β的关系
通过上面的演示,我们看到有时两个角的和是180°,也就是两个角之和正好成一平角,在这种情况下,我们给出互为补角定义:
如果两个角的和是一个平角,那么这两个角互为补角180°.简称互补.用数学式子表示为:因为∠1+∠2=180°,所以∠1与∠2互补.反之,因为∠1与∠2互补,所以∠1+∠2=180°.
找朋友:图中给出的各角,那些互为补角?
教师活动:用多媒体演示
活动三
1、你能正确完成下面内容吗?
若∠1 + ∠2 =180 °, ( 已知 )
则 . ( )
若∠1和∠2互补, ( 已知 )
则 . ( )
若∠3 + ∠4 =90 °, ( 已知 )则 . ( )
若∠3和∠4互余, ( 已知 )
则 .( )
2、你能快速完成下面的内容吗?
∠A的度数 50 X (0<X<90)
∠A的余角 45
∠A的补角 120
需要注意的几点:
①互余与互补是指两个角之间的关系,不能说单独的一个角是余角或补角,但可以说一个角是某一个角的余角或补角.
②两个角是否互余或互补只跟这两个角的大小有关,与它们的位置无关,不要误认为互余或互补的角必须相邻.
知识抢答
判断:
1.如果∠1=30°,∠2=25°,∠3=35°,那么∠1、∠2、∠3这三个角称为互为余( )
2.两块直角三角板中∠A=90°,∠D=90°,则∠A与∠D互为补角。( )
开动脑筋
如图,O为直线AB上一点,∠AOD=900,则图中哪些角互为余角?哪些角互为补角?
活动四:
画一画 想一想1
(1) 已知∠α,请利用三角板画的∠α的余角
(2)图中∠α的余角∠1,∠2的大小有什么关系?为什么?
(3) 聪明的你发现了怎么结论?
我发现:同(等)角的余角相等
画一画 想一想2
已知∠α,请利用三角板画的∠α的补角
聪明的你发现了怎么结论?
我来说:同 (等)角的补角相等
及时应用
1. 如图,∠1+∠2=180,∠1+∠3=180,∠2与∠3的大小关系是_________,理由:_______________.
2.如图,直线CD经过点O,且OC平分∠AOB。∠AOD与∠BOD有怎样的大小关系?说明你的理由。
3、如图, ∠AOB=∠COD=90 °,则∠1与∠3有怎样的大小关系?说
明你的理由。
能力拓展
已知一个角的补角是这个角的余角的4倍,求这个角的度数。
解:设这个角为x°,则它的余角为(90-x) °,它的补角为(180-x) °,得 180-x=4(90-x)
180-x=360-4x
-x+4x=360-18
3x=180
X=60
答:这个角是60o。
三、议一议. 今天我们都哪些收获?
互为补角 互为余角
对应图形
数量关系 ∠1+ ∠2 = 90 ° ∠1+ ∠2 = 180 °
性 质 同角或等角的余角相等。 同角或等角的补角相等。
四、今天你需要完成的任务是:
1.课本第140页 7题,8题,第141页11题,12题,13题.
2.∠α的余角是它的3倍,∠α是多少度?
3.(选做题)一个角的余角比这个角的补角的 还小10°,求这个角的余角及这个角的补角的度数.(用两种方法求解)
五、课后反思
(3)
(1)
(2)
O
A
B
1
2
O
A
B
C
由上面操作,你知道 与∠AOB有什么关系吗?
你是怎样判断的?
1
2
3
1
2
1
2
教学目标:
1、知识与技能:
在具体的现实情境中,认识一个角的余角和补角,掌握余角和补角的性质及简单应用
2、过程与方法:
通过活动提高学生的抽象概括能力,发展空间观念和知识运用能力,学会简单的逻辑推理,并能对问题的结论进行合理的猜想。
3、情感态度与价值观:
体会观察、归纳、推理对数学知识中获取数学猜想和论证的重要作用,初步数学中推理的严谨性和结论的确定性,能在独立思考和小组交流中获益。
重、难点:
1、重点:认识角的互余、互补关系及其性质,是本节课的重点。
2、难点:通过简单的推理,归纳出余角、补角的性质,并能用规范的语言描述性质是难点。
一、引入新课:
1问题引入 :回顾平角、周角定义
2明确目标:a余角与补角概念b余角性质与补角性质C概念及性质的应用
二、新知探究
活动一
请同学们拿出三角板并观察三角板每个角的度数,分小组用三角板拼图,要求用三角板的两个锐角组成直角。
(让学生说出自己的方法:可以测量,也可以剪纸板拼等等,学生的方法只要合理就应鼓励)
教师活动:用多媒体演示
通过上面的演示,我们看到有时两个角的和是90°,也就是两个角之和正好成一直角,在这种情况下,我们给出互为余角概念
互为余角定义:如果两个锐角的和是一个直角90°,那么这两个角互为余角.简称互余.用数学式子表示为:因为∠1+∠2=90°,所以∠1与∠2互余.反之,因为∠1与∠2互余,所以∠1+∠2=90°
找朋友:图中给出的各角,那些互为余角?
教师活动:用多媒体演示
变式练习:如图,将一三角板的直角顶点放在直线上(三角板和直线在同一平面内),随意绕该顶点在同一平面内转动三角板(三角板总在直线的上方),
问∠1与∠2的和是否会发生变化?
活动二:
将自己准备好的长方形硬纸板沿一条直线剪开,如下图所示
观察与思考:教师用多媒体演示 ∠α与∠β的关系
通过上面的演示,我们看到有时两个角的和是180°,也就是两个角之和正好成一平角,在这种情况下,我们给出互为补角定义:
如果两个角的和是一个平角,那么这两个角互为补角180°.简称互补.用数学式子表示为:因为∠1+∠2=180°,所以∠1与∠2互补.反之,因为∠1与∠2互补,所以∠1+∠2=180°.
找朋友:图中给出的各角,那些互为补角?
教师活动:用多媒体演示
活动三
1、你能正确完成下面内容吗?
若∠1 + ∠2 =180 °, ( 已知 )
则 . ( )
若∠1和∠2互补, ( 已知 )
则 . ( )
若∠3 + ∠4 =90 °, ( 已知 )则 . ( )
若∠3和∠4互余, ( 已知 )
则 .( )
2、你能快速完成下面的内容吗?
∠A的度数 50 X (0<X<90)
∠A的余角 45
∠A的补角 120
需要注意的几点:
①互余与互补是指两个角之间的关系,不能说单独的一个角是余角或补角,但可以说一个角是某一个角的余角或补角.
②两个角是否互余或互补只跟这两个角的大小有关,与它们的位置无关,不要误认为互余或互补的角必须相邻.
知识抢答
判断:
1.如果∠1=30°,∠2=25°,∠3=35°,那么∠1、∠2、∠3这三个角称为互为余( )
2.两块直角三角板中∠A=90°,∠D=90°,则∠A与∠D互为补角。( )
开动脑筋
如图,O为直线AB上一点,∠AOD=900,则图中哪些角互为余角?哪些角互为补角?
活动四:
画一画 想一想1
(1) 已知∠α,请利用三角板画的∠α的余角
(2)图中∠α的余角∠1,∠2的大小有什么关系?为什么?
(3) 聪明的你发现了怎么结论?
我发现:同(等)角的余角相等
画一画 想一想2
已知∠α,请利用三角板画的∠α的补角
聪明的你发现了怎么结论?
我来说:同 (等)角的补角相等
及时应用
1. 如图,∠1+∠2=180,∠1+∠3=180,∠2与∠3的大小关系是_________,理由:_______________.
2.如图,直线CD经过点O,且OC平分∠AOB。∠AOD与∠BOD有怎样的大小关系?说明你的理由。
3、如图, ∠AOB=∠COD=90 °,则∠1与∠3有怎样的大小关系?说
明你的理由。
能力拓展
已知一个角的补角是这个角的余角的4倍,求这个角的度数。
解:设这个角为x°,则它的余角为(90-x) °,它的补角为(180-x) °,得 180-x=4(90-x)
180-x=360-4x
-x+4x=360-18
3x=180
X=60
答:这个角是60o。
三、议一议. 今天我们都哪些收获?
互为补角 互为余角
对应图形
数量关系 ∠1+ ∠2 = 90 ° ∠1+ ∠2 = 180 °
性 质 同角或等角的余角相等。 同角或等角的补角相等。
四、今天你需要完成的任务是:
1.课本第140页 7题,8题,第141页11题,12题,13题.
2.∠α的余角是它的3倍,∠α是多少度?
3.(选做题)一个角的余角比这个角的补角的 还小10°,求这个角的余角及这个角的补角的度数.(用两种方法求解)
五、课后反思
(3)
(1)
(2)
O
A
B
1
2
O
A
B
C
由上面操作,你知道 与∠AOB有什么关系吗?
你是怎样判断的?
1
2
3
1
2
1
2
