人教版七年级数学上册3.1.2等式的性质 教学设计
文档属性
| 名称 | 人教版七年级数学上册3.1.2等式的性质 教学设计 |  | |
| 格式 | docx | ||
| 文件大小 | 191.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-19 17:06:26 | ||
图片预览

文档简介
教学设计:3.1.2 等式的性质
教学目标:
1.知道等式的性质;
2.会用等式的性质解简单的一元一次方程;
3. 培养学生观察、分析、概括及逻辑思维能力;
4. 渗透“化归”的思想.
教学重点: 理解并掌握等式的性质。
教学难点: 会用等式的性质解简单的一元一次方程。
教学过程:
温故知新:
1、什么叫方程
2、什么叫一元一次方程?
3、什么叫方程的解?
4、你能想出下列方程的解吗?
5、我来辨别 :①4+x=7, ② 2x, ③ 3x+1,
④ a+b=b+a, ⑤ a2+b2 ⑥ c=2πr
⑦ 1+2=3, ⑧ ab, ⑨ S= ah,
⑩ 2x-3y>0
上述这组式子中,( )是等式, ( ) 不是等式。
师生活动:1、2、3题学生口答,教师评价。第4题(1)、(2)学生很快能想出,但(3)、(4)很费力,教师及时指出除了特别简单的方程,大部分方程不能直接想出方程的解。第5题辨别等式,学生共同得出。
探索新知 :
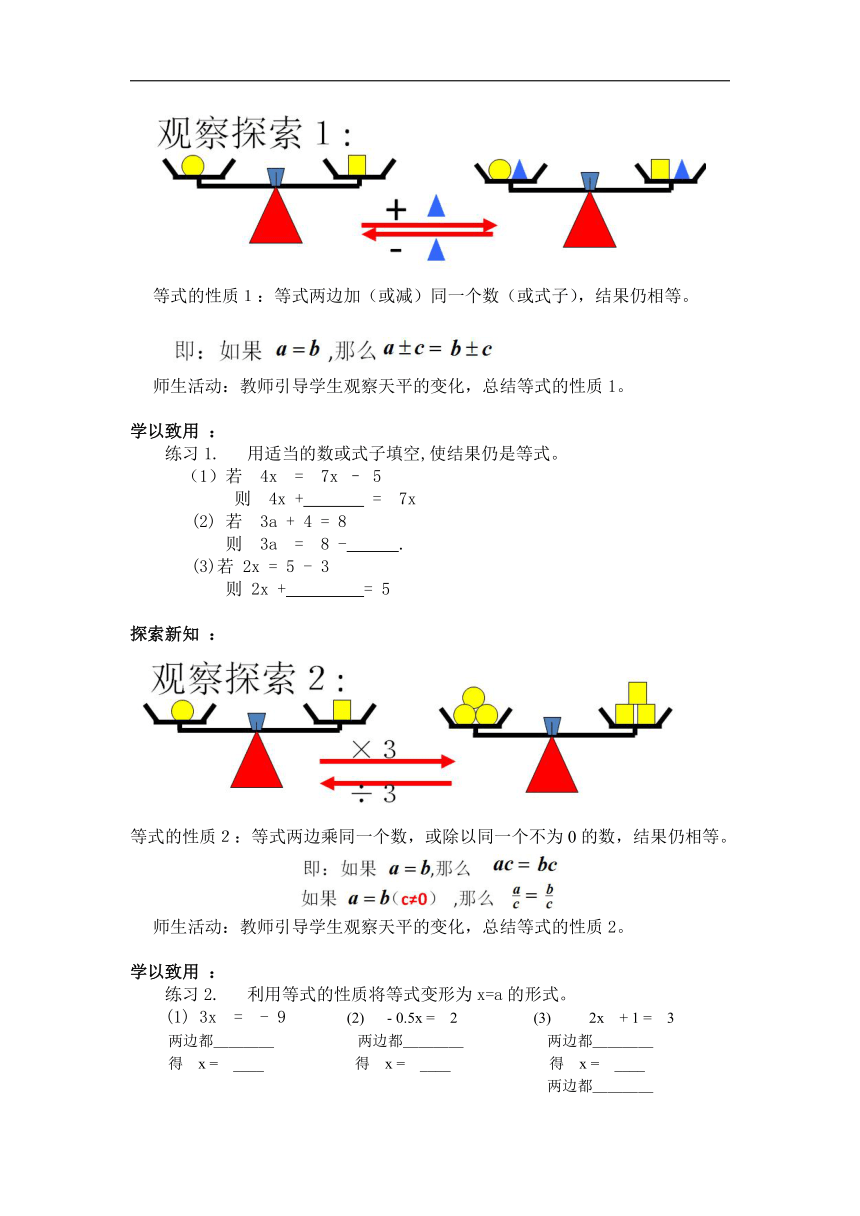
等式的性质1:等式两边加(或减)同一个数(或式子),结果仍相等。
师生活动:教师引导学生观察天平的变化,总结等式的性质1。
学以致用 :
练习1. 用适当的数或式子填空,使结果仍是等式。
(1)若 4x = 7x – 5
则 4x + = 7x
(2) 若 3a + 4 = 8
则 3a = 8 - .
(3)若 2x = 5 - 3
则 2x + = 5
探索新知 :
等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍相等。
师生活动:教师引导学生观察天平的变化,总结等式的性质2。
学以致用 :
练习2. 利用等式的性质将等式变形为x=a的形式。
(1) 3x = - 9 (2) - 0.5x = 2 (3) 2x + 1 = 3
两边都____ 两边都____ 两边都____
得 x = ____ 得 x = ____ 得 x = ____
两边都____
得 x = ____
归纳等式的两个性质
等式的性质1: 等式两边加(或减)同一个数(或式子),结果仍相等。
等式的性质2: 等式两边乘同一个数,或除以同一个不为0数,结果仍相等。
学以致用 :
判断对错,对的说明根据等式的哪一条性质;错的说出为什么。
(1)如果x=y,那么 ( )
(2)如果x=y,那么 ( )
(3)如果x=y,那么 ( )
(4)如果x=y,那么 ( )
(5)如果x=y,那么 ( )
注意事项:
用等式的性质变形时,
边必须同时进行计算;
②加(或减),乘(或除以)的数必须是同一个数;
③除数不能为0.
巩固训练
1.填空
① 若 x-2 = 3,根据_______________,得到 x-2 +2 = 3 +2 ,即 x = 5 。
② 若 -4 x = 3,根据______________,得到 , 即x =____ 。
2.填一填:
(1) 如果x+4=7 , 那么x=_____ , 其依据是
________ ,在等式的两边都________.
(2) 如果 - 2x= 8 , 那么x =________,其依据是
________ ,在等式的两边都________.
(3) 如果 –x = 3, 那么 x =________
(4) 如果 - 2x = 4, 那么x =________。
(5) 如果2x - , 那么2x =___,所以x =___.
3.下列各式的变形正确的是( )
A.由 ,得到 x = 2
B.由 ,得到 x = 1
C.由-2 a = -3,得到 a =
D.由 x-1 = 4,得到 x = 5
4、填依据:在下列各题的括号内,填上使等式成立的依据.
5.判断对错,对的请说出根据等式的哪 一条性质,错的请说出为什么。
师生活动:教师带领学生逐题完成巩固练习,及时订正,适时鼓励。
例题精讲
例:利用等式的性质解下列方程
小试牛刀
利用等式的性质解下列方程并检验。
师生活动:师生共同完成例题,学生独立完成小试牛刀,订正,统计正确率。
课堂小结:
这节课你有哪些收获?
师生活动:学生说收获、谈感受,梳理本节课所学内容。
布置作业:
1.数学课本P83页
习题3.1第4、5、6题
2.数学同步训练P68-70页
教学目标:
1.知道等式的性质;
2.会用等式的性质解简单的一元一次方程;
3. 培养学生观察、分析、概括及逻辑思维能力;
4. 渗透“化归”的思想.
教学重点: 理解并掌握等式的性质。
教学难点: 会用等式的性质解简单的一元一次方程。
教学过程:
温故知新:
1、什么叫方程
2、什么叫一元一次方程?
3、什么叫方程的解?
4、你能想出下列方程的解吗?
5、我来辨别 :①4+x=7, ② 2x, ③ 3x+1,
④ a+b=b+a, ⑤ a2+b2 ⑥ c=2πr
⑦ 1+2=3, ⑧ ab, ⑨ S= ah,
⑩ 2x-3y>0
上述这组式子中,( )是等式, ( ) 不是等式。
师生活动:1、2、3题学生口答,教师评价。第4题(1)、(2)学生很快能想出,但(3)、(4)很费力,教师及时指出除了特别简单的方程,大部分方程不能直接想出方程的解。第5题辨别等式,学生共同得出。
探索新知 :
等式的性质1:等式两边加(或减)同一个数(或式子),结果仍相等。
师生活动:教师引导学生观察天平的变化,总结等式的性质1。
学以致用 :
练习1. 用适当的数或式子填空,使结果仍是等式。
(1)若 4x = 7x – 5
则 4x + = 7x
(2) 若 3a + 4 = 8
则 3a = 8 - .
(3)若 2x = 5 - 3
则 2x + = 5
探索新知 :
等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍相等。
师生活动:教师引导学生观察天平的变化,总结等式的性质2。
学以致用 :
练习2. 利用等式的性质将等式变形为x=a的形式。
(1) 3x = - 9 (2) - 0.5x = 2 (3) 2x + 1 = 3
两边都____ 两边都____ 两边都____
得 x = ____ 得 x = ____ 得 x = ____
两边都____
得 x = ____
归纳等式的两个性质
等式的性质1: 等式两边加(或减)同一个数(或式子),结果仍相等。
等式的性质2: 等式两边乘同一个数,或除以同一个不为0数,结果仍相等。
学以致用 :
判断对错,对的说明根据等式的哪一条性质;错的说出为什么。
(1)如果x=y,那么 ( )
(2)如果x=y,那么 ( )
(3)如果x=y,那么 ( )
(4)如果x=y,那么 ( )
(5)如果x=y,那么 ( )
注意事项:
用等式的性质变形时,
边必须同时进行计算;
②加(或减),乘(或除以)的数必须是同一个数;
③除数不能为0.
巩固训练
1.填空
① 若 x-2 = 3,根据_______________,得到 x-2 +2 = 3 +2 ,即 x = 5 。
② 若 -4 x = 3,根据______________,得到 , 即x =____ 。
2.填一填:
(1) 如果x+4=7 , 那么x=_____ , 其依据是
________ ,在等式的两边都________.
(2) 如果 - 2x= 8 , 那么x =________,其依据是
________ ,在等式的两边都________.
(3) 如果 –x = 3, 那么 x =________
(4) 如果 - 2x = 4, 那么x =________。
(5) 如果2x - , 那么2x =___,所以x =___.
3.下列各式的变形正确的是( )
A.由 ,得到 x = 2
B.由 ,得到 x = 1
C.由-2 a = -3,得到 a =
D.由 x-1 = 4,得到 x = 5
4、填依据:在下列各题的括号内,填上使等式成立的依据.
5.判断对错,对的请说出根据等式的哪 一条性质,错的请说出为什么。
师生活动:教师带领学生逐题完成巩固练习,及时订正,适时鼓励。
例题精讲
例:利用等式的性质解下列方程
小试牛刀
利用等式的性质解下列方程并检验。
师生活动:师生共同完成例题,学生独立完成小试牛刀,订正,统计正确率。
课堂小结:
这节课你有哪些收获?
师生活动:学生说收获、谈感受,梳理本节课所学内容。
布置作业:
1.数学课本P83页
习题3.1第4、5、6题
2.数学同步训练P68-70页
