26.1.2 反比例函数的图象和性质(第2课时) 教案+学案+课件(共26张PPT)
文档属性
| 名称 | 26.1.2 反比例函数的图象和性质(第2课时) 教案+学案+课件(共26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-19 11:19:04 | ||
图片预览







文档简介
(共24张PPT)
2022年春人教版数学
九年级下册数学精品课件
26.1.2 反比例函数的图象和性质
(第2课时)
2.会用待定系数法求反比例函数解析式.
1.使学生进一步理解和掌握反比例函数的图象及性质.
3.能灵活运用函数图象和性质解决一些较综合的问题.
学习目标
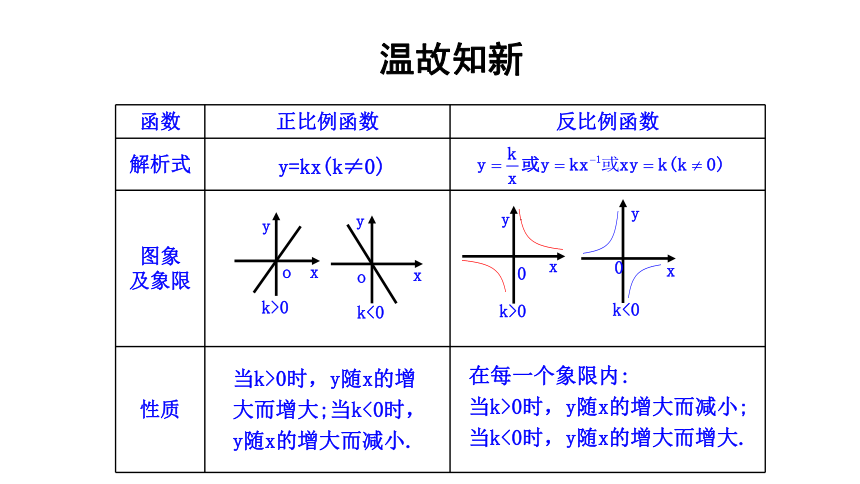
函数 正比例函数 反比例函数
解析式
图象
及象限
性质
在每一个象限内:
当k>0时,y随x的增大而减小;
当k<0时,y随x的增大而增大.
y=kx(k≠0)
当k>0时,y随x的增大而增大;当k<0时,y随x的增大而减小.
k<0
x
y
o
x
y
o
k>0
k<0
y
x
0
y
0
k>0
x
温故知新
例题
m﹥0
m -5= -1
所以必须满足{
1.已知反比例函数y=mxm -5,它的两个分支分别在第一、第三象限,求m的值?
得 m =2
【解析】因为反比例函数y=mxm -5,它的两个分支分别在第一、第三象限,
y=mxm -5
x
y
0
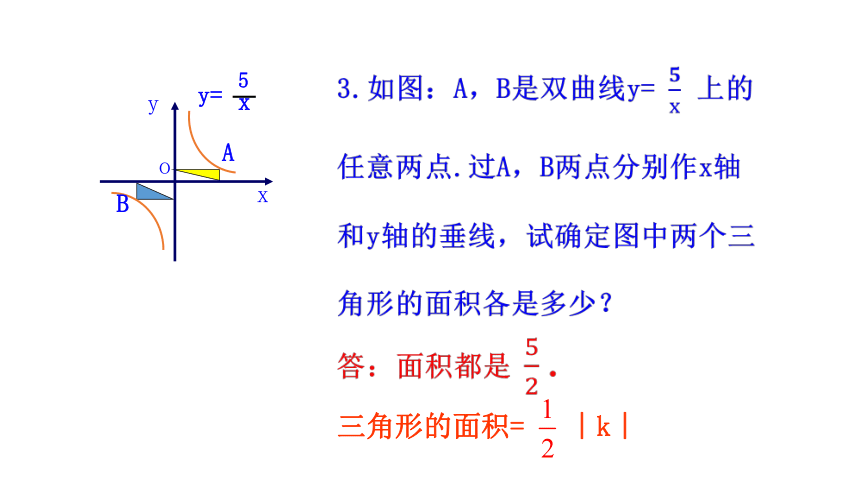
跟踪训练
2.根据图中点的坐标
(1)求出y与x的函数解析式.
(2)如果点A(-2,b)在双曲线上,求b的值.
A(-2,b)
(3,-1)
x
0
(3)比较绿色部分和黄色部分的面积的大小.
.
B
y
(3)绿色部分和黄色部分的面积相等,都等于︱k︱
答案:(1) (2)
x
y
o
A
y=
5
x
B
三角形的面积= ︱k︱
例4.(成都·中考)如图,已
知反比例函数 与一次函数y=x+b的
图象在第一象限相交于点A(1,-k+4).
(1)试确定这两个函数的解析式.
(2)求出这两个函数图象的另一个交点B的坐标,并根据图象写出反比例函数的值大于一次函数的值的x的取值范围.
例题
【解析】(1)把A点坐标代入反比例函数解析式得:-k+4=k,
解得k=2,把A(1,2)代入y=x+b
得b=1,∴这两个函数的解析式为:
y= 和y=x+1.
(2)由方程组
∴B点的坐标为(-2,-1).
由图象得反比例函数的值大于一次函数的值的x的取值范围是:0<x<1或x<-2.
跟踪训练
跟踪训练
3.(江津·中考)已知如图,A是反比例函
数 的图象上的一点,AB⊥x轴于点B,
且△ABO的面积是3,则k的值是( )
(A)3 (B)-3 (C)6 (D)-6
【解析】选C.设A点的坐标为(a,b),则k=ab,△ABO的
面积为 ,所以ab=6,即k=6
5.(威海·中考)如图,一次函数y=kx+b的图象与反比
例函数 的图象交于点A(-2,-5),C(5,n),
交y轴于点B,交x轴于点D.
(1)求反比例函数 和一次函数
y=kx+b的解析式;
(2)连接OA,OC.求△AOC的面积.
【解析】(1)∵反比例函数 的图象经过点A(-2,-5),∴m=(-2)×(-5)=10.
∴反比例函数的解析式为
∵点C(5,n)在反比例函数的图象上,
∴n= =2.
∴C的坐标为(5,2).
∵一次函数的图象经过点A,C,将这两个点的坐标代入y=kx+b,得
∴所求一次函数的解析式为y=x-3.
(2)∵一次函数y=x-3的图象交y轴于点B,
∴B点坐标为(0,-3)
∴OB=3.
∵A点的横坐标为-2,C点的横坐标为5,
∴S△AOC=S△AOB+S△BOC= · OB · |-2|+ · OB · 5
= · OB ·(2+5)=
通过本课时的学习,需要我们
1.熟练掌握反比例函数的图象及性质.
2.能用待定系数法求反比例函数解析式.
3.灵活运用函数图象和性质解决一些较综合的问题.
课堂小结
https://www.21cnjy.com/help/help_extract.php
2022年春人教版数学
九年级下册数学精品课件
26.1.2 反比例函数的图象和性质
(第2课时)
2.会用待定系数法求反比例函数解析式.
1.使学生进一步理解和掌握反比例函数的图象及性质.
3.能灵活运用函数图象和性质解决一些较综合的问题.
学习目标
函数 正比例函数 反比例函数
解析式
图象
及象限
性质
在每一个象限内:
当k>0时,y随x的增大而减小;
当k<0时,y随x的增大而增大.
y=kx(k≠0)
当k>0时,y随x的增大而增大;当k<0时,y随x的增大而减小.
k<0
x
y
o
x
y
o
k>0
k<0
y
x
0
y
0
k>0
x
温故知新
例题
m﹥0
m -5= -1
所以必须满足{
1.已知反比例函数y=mxm -5,它的两个分支分别在第一、第三象限,求m的值?
得 m =2
【解析】因为反比例函数y=mxm -5,它的两个分支分别在第一、第三象限,
y=mxm -5
x
y
0
跟踪训练
2.根据图中点的坐标
(1)求出y与x的函数解析式.
(2)如果点A(-2,b)在双曲线上,求b的值.
A(-2,b)
(3,-1)
x
0
(3)比较绿色部分和黄色部分的面积的大小.
.
B
y
(3)绿色部分和黄色部分的面积相等,都等于︱k︱
答案:(1) (2)
x
y
o
A
y=
5
x
B
三角形的面积= ︱k︱
例4.(成都·中考)如图,已
知反比例函数 与一次函数y=x+b的
图象在第一象限相交于点A(1,-k+4).
(1)试确定这两个函数的解析式.
(2)求出这两个函数图象的另一个交点B的坐标,并根据图象写出反比例函数的值大于一次函数的值的x的取值范围.
例题
【解析】(1)把A点坐标代入反比例函数解析式得:-k+4=k,
解得k=2,把A(1,2)代入y=x+b
得b=1,∴这两个函数的解析式为:
y= 和y=x+1.
(2)由方程组
∴B点的坐标为(-2,-1).
由图象得反比例函数的值大于一次函数的值的x的取值范围是:0<x<1或x<-2.
跟踪训练
跟踪训练
3.(江津·中考)已知如图,A是反比例函
数 的图象上的一点,AB⊥x轴于点B,
且△ABO的面积是3,则k的值是( )
(A)3 (B)-3 (C)6 (D)-6
【解析】选C.设A点的坐标为(a,b),则k=ab,△ABO的
面积为 ,所以ab=6,即k=6
5.(威海·中考)如图,一次函数y=kx+b的图象与反比
例函数 的图象交于点A(-2,-5),C(5,n),
交y轴于点B,交x轴于点D.
(1)求反比例函数 和一次函数
y=kx+b的解析式;
(2)连接OA,OC.求△AOC的面积.
【解析】(1)∵反比例函数 的图象经过点A(-2,-5),∴m=(-2)×(-5)=10.
∴反比例函数的解析式为
∵点C(5,n)在反比例函数的图象上,
∴n= =2.
∴C的坐标为(5,2).
∵一次函数的图象经过点A,C,将这两个点的坐标代入y=kx+b,得
∴所求一次函数的解析式为y=x-3.
(2)∵一次函数y=x-3的图象交y轴于点B,
∴B点坐标为(0,-3)
∴OB=3.
∵A点的横坐标为-2,C点的横坐标为5,
∴S△AOC=S△AOB+S△BOC= · OB · |-2|+ · OB · 5
= · OB ·(2+5)=
通过本课时的学习,需要我们
1.熟练掌握反比例函数的图象及性质.
2.能用待定系数法求反比例函数解析式.
3.灵活运用函数图象和性质解决一些较综合的问题.
课堂小结
https://www.21cnjy.com/help/help_extract.php
