北师大版八年级数学下册 第四章《因式分解》名校优选检测题【含答案】
文档属性
| 名称 | 北师大版八年级数学下册 第四章《因式分解》名校优选检测题【含答案】 |  | |
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-19 12:43:49 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
北师大版八年级数学下册 第四章 名校优选检测题
(满分120分,考试用时120分钟)
姓名:________ 班级:________ 分数:________
一、选择题(每小题3分,共30分)
1.下列等式中,从左到右的变形中是因式分解的是( )
A.9x2-6x+1=(3x-1)2 B.x2-4x+1=x(x-4)+1
C.3m(m-n)=3m2-3mn D.x+3y=(x+y)+2y
2.将多项式-6a3b2+2a2b2因式分解时,应提取的公因式是( )
A.-2a2b2 B.-2ab C.-2a2b D.-2a3b3
3.有下列各式:①x2+y2;②4x2-y2;③-x2-9y2;④-x2+y2;⑤x2-4xy+4y2;⑥m2-9m.其中可用平方差公式因式分解的有( )
A.1个 B.2个 C.3个 D.4个
4.在多项式①x2+xy-y2;②-x2+2xy-y2;③xy+x2+y2;④1-x+中,能用完全平方公式因式分解的是( )
A.①② B.①③ C.②④ D.①④
5.把多项式4a2b+4ab2+b3因式分解,正确的是( )
A.a(2a+b)2 B.b(2a+b)2 C.(a+2b)2 D.4b(a+b)2
6.若多项式x2+mx-28可因式分解为(x-4)(x+7),则m的值为( )
A.-3 B.11 C.-11 D.3
7.在边长为a的正方形中挖去一个边长为b的小正方形(a>b),再沿虚线剪开(如图①),然后拼成一个等腰梯形(如图②),根据这两个图形的面积关系,表明下列式子中成立的是( )
A.a2-b2=(a+b)(a-b) B.(a+b)2=a2+2ab+b2
C.(a-b)2=a2-2ab+b2 D.a2-b2=(a-b)2
8.对于任意整数m,多项式(4m-5)2-9都能被下列选项整除的是( )
A.8 B.m C.m-1 D.m+2
9.小强是一位密码编译爱好者,在他的密码手册中,有这样一条信息:a-b,x-y,x+y,a+b,x2-y2,a2-b2分别对应下列六个字:家,爱,我,乡,游,美,现将(x2-y2)a2-(x2-y2)b2因式分解,结果呈现的密码信息可能是( )
A.我爱美 B.家乡游 C.爱我家乡 D.美我家乡
10.一个三角形的两边长为x,y,且使x3+x2y-xy2-y3=0,则此三角形的形状按边分一定为( )
A.等腰三角形 B.等边三角形 C.不等边三角形 D.无法判断
二、填空题(每小题3分,共24分)
11.(x+3)(2x-1)是多项式 因式分解的结果.
12.请在二项式x2-□y2的□里面添加一个式子,使其能因式分解,在“□”中添加的式子是 (写出一个即可).
13.(宜宾中考)分解因式:xy2-4x= .
14.(苏州中考)若a+b=4,a-b=1,则(a+1)2-(b-1)2的值为 .
15.甲、乙两同学因式分解x2+mx+n,甲看错了n,分解结果为(x+2)(x+4);乙看错了m,分解结果为(x+1)(x+9),则正确的因式分解结果是 .
在一个边长为12.75 cm的正方形内挖去一个边长为7.25 cm的正方形,则剩下部分的面积为 cm2.
17.已知a,b,c为△ABC的三边,试判断(a+b)2-c2的值 (选填“大于”“小于”或“等于”)零.
18.阅读下列文字与例题:
将一个多项式分组后,可提公因式或运用公式继续分解的方法是分组分解法.
例如:(1)am+an+bm+bn=(am+bm)+(an+bn)=m(a+b)+n(a+b)=(a+b)(m+n).
(2)x2-y2-2y-1=x2-(y2+2y+1)=x2-(y+1)2=(x+y+1)(x-y-1).
试用上述方法因式分解a2+2ab+ac+bc+b2= .
三、解答题(共66分)
19.(8分)分解因式:
(1)6x3-24x; (2)(a+b)2-4(a+b-1).
20.(10分)利用分解因式方法简便计算:40×3.52+80×3.5×1.5+40×1.52.
21.(12分)先分解因式,再计算求值.
(1)已知a-b=5,ab=3,求代数式a3b-a2b2+ab3的值;
(2)(2x-3y)2-(2x+3y)2,其中x=,y=.
22.(12分)数学知识奥妙无穷,小玉观察下面的算式:
72-12=48=12×4;
82-22=60=12×5;
92-32=72=12×6;
102-42=84=12×7;
…
从中惊奇地发现:这些算式均为12的倍数,但却不知其中的原因,她非常纳闷,请利用所学的知识给小玉解释一下.
23.(12分)小刚碰到一道题目:“分解因式x2+2x-3”,不会做,去问老师,老师说:“能否变成平方差的形式?把原式加上1,再减去1,这样原式化为(x2+2x+1)-4,…”,老师话没讲完,小刚就恍然大悟,他马上就做好了此题.
(1)请完成他因式分解的步骤;
(2)运用这种方法因式分解:a2-2ab-3b2.
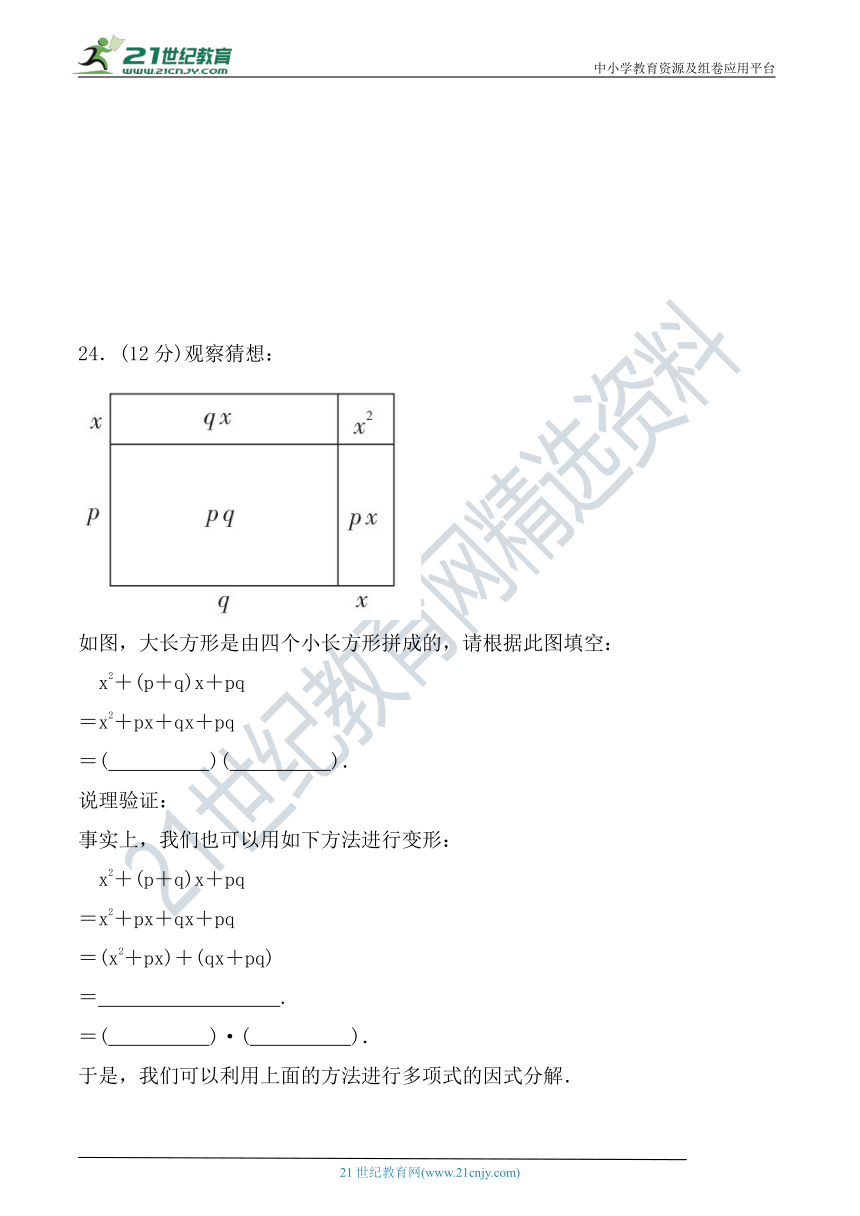
24.(12分)观察猜想:
如图,大长方形是由四个小长方形拼成的,请根据此图填空:
x2+(p+q)x+pq
=x2+px+qx+pq
=( )( ).
说理验证:
事实上,我们也可以用如下方法进行变形:
x2+(p+q)x+pq
=x2+px+qx+pq
=(x2+px)+(qx+pq)
= .
=( )·( ).
于是,我们可以利用上面的方法进行多项式的因式分解.
尝试运用:
例题:把x2+3x+2因式分解.
解:x2+3x+2=x2+(2+1)x+2×1=(x+2)(x+1).
请利用上述方法将下列多项式因式分解.
(1)y2+6y+5;
(2)x2-2x-8;
(3)(y2+y)2+7(y2+y)-18.
参考答案
一、选择题(每小题3分,共30分)
1.下列等式中,从左到右的变形中是因式分解的是(A)
A.9x2-6x+1=(3x-1)2 B.x2-4x+1=x(x-4)+1
C.3m(m-n)=3m2-3mn D.x+3y=(x+y)+2y
2.将多项式-6a3b2+2a2b2因式分解时,应提取的公因式是(A)
A.-2a2b2 B.-2ab C.-2a2b D.-2a3b3
3.有下列各式:①x2+y2;②4x2-y2;③-x2-9y2;④-x2+y2;⑤x2-4xy+4y2;⑥m2-9m.其中可用平方差公式因式分解的有(B)
A.1个 B.2个 C.3个 D.4个
4.在多项式①x2+xy-y2;②-x2+2xy-y2;③xy+x2+y2;④1-x+中,能用完全平方公式因式分解的是(C)
A.①② B.①③ C.②④ D.①④
5.把多项式4a2b+4ab2+b3因式分解,正确的是(B)
A.a(2a+b)2 B.b(2a+b)2 C.(a+2b)2 D.4b(a+b)2
6.若多项式x2+mx-28可因式分解为(x-4)(x+7),则m的值为(D)
A.-3 B.11 C.-11 D.3
7.在边长为a的正方形中挖去一个边长为b的小正方形(a>b),再沿虚线剪开(如图①),然后拼成一个等腰梯形(如图②),根据这两个图形的面积关系,表明下列式子中成立的是(A)
A.a2-b2=(a+b)(a-b) B.(a+b)2=a2+2ab+b2
C.(a-b)2=a2-2ab+b2 D.a2-b2=(a-b)2
8.对于任意整数m,多项式(4m-5)2-9都能被下列选项整除的是(A)
A.8 B.m C.m-1 D.m+2
9.小强是一位密码编译爱好者,在他的密码手册中,有这样一条信息:a-b,x-y,x+y,a+b,x2-y2,a2-b2分别对应下列六个字:家,爱,我,乡,游,美,现将(x2-y2)a2-(x2-y2)b2因式分解,结果呈现的密码信息可能是(C)
A.我爱美 B.家乡游 C.爱我家乡 D.美我家乡
10.一个三角形的两边长为x,y,且使x3+x2y-xy2-y3=0,则此三角形的形状按边分一定为(A)
A.等腰三角形 B.等边三角形 C.不等边三角形 D.无法判断
二、填空题(每小题3分,共24分)
11.(x+3)(2x-1)是多项式2x2+5x-3因式分解的结果.
12.请在二项式x2-□y2的□里面添加一个式子,使其能因式分解,在“□”中添加的式子是4(答案不唯一)(写出一个即可).
13.(宜宾中考)分解因式:xy2-4x=x(y+2)(y-2).
14.(苏州中考)若a+b=4,a-b=1,则(a+1)2-(b-1)2的值为12.
15.甲、乙两同学因式分解x2+mx+n,甲看错了n,分解结果为(x+2)(x+4);乙看错了m,分解结果为(x+1)(x+9),则正确的因式分解结果是(x+3)2.
在一个边长为12.75 cm的正方形内挖去一个边长为7.25 cm的正方形,则剩下部分的面积为110 cm2.
17.已知a,b,c为△ABC的三边,试判断(a+b)2-c2的值大于(选填“大于”“小于”或“等于”)零.
18.阅读下列文字与例题:
将一个多项式分组后,可提公因式或运用公式继续分解的方法是分组分解法.
例如:(1)am+an+bm+bn=(am+bm)+(an+bn)=m(a+b)+n(a+b)=(a+b)(m+n).
(2)x2-y2-2y-1=x2-(y2+2y+1)=x2-(y+1)2=(x+y+1)(x-y-1).
试用上述方法因式分解a2+2ab+ac+bc+b2=(a+b)(a+b+c).
三、解答题(共66分)
19.(8分)分解因式:
(1)6x3-24x;
解:原式=6x(x2-4)
=6x(x+2)(x-2).
(2)(a+b)2-4(a+b-1).
解:原式=(a+b)2-4(a+b)+4
=(a+b-2)2.
20.(10分)利用分解因式方法简便计算:40×3.52+80×3.5×1.5+40×1.52.
解:40×3.52+80×3.5×1.5+40×1.52
=40×(3.5+1.5)2
=40×52
=1 000.
21.(12分)先分解因式,再计算求值.
(1)已知a-b=5,ab=3,求代数式a3b-a2b2+ab3的值;
解:∵a3b-a2b2+ab3=ab(a2-2ab+b2)
=ab(a-b)2,
而ab=3,a-b=5,
∴原式=×3×52=.
(2)(2x-3y)2-(2x+3y)2,其中x=,y=.
解: (2x-3y)2-(2x+3y)2
=(2x-3y+2x+3y)(2x-3y-2x-3y)
=4x·(-6y)
=-24xy,
把x=,y=代入得
原式=-24××=-.
22.(12分)数学知识奥妙无穷,小玉观察下面的算式:
72-12=48=12×4;
82-22=60=12×5;
92-32=72=12×6;
102-42=84=12×7;
…
从中惊奇地发现:这些算式均为12的倍数,但却不知其中的原因,她非常纳闷,请利用所学的知识给小玉解释一下.
解:根据上述规律可知,第n个式子左边可表示为(n+6)2-n2,
∴(n+6)2-n2=(n+6+n)(n+6-n)=2(n+3)·6=12(n+3).
∵n为正整数,∴(n+6)2-n2是12的倍数.
23.(12分)小刚碰到一道题目:“分解因式x2+2x-3”,不会做,去问老师,老师说:“能否变成平方差的形式?把原式加上1,再减去1,这样原式化为(x2+2x+1)-4,…”,老师话没讲完,小刚就恍然大悟,他马上就做好了此题.
(1)请完成他因式分解的步骤;
(2)运用这种方法因式分解:a2-2ab-3b2.
解:(1)x2+2x-3=(x2+2x+1)-4
=(x+1)2-22
=(x+1+2)(x+1-2)
=(x+3)(x-1).
(2)a2-2ab-3b2=a2-2ab+b2-4b2
=(a-b)2-4b2
=(a-b+2b)(a-b-2b)
=(a+b)(a-3b).
24.(12分)观察猜想:
如图,大长方形是由四个小长方形拼成的,请根据此图填空:
x2+(p+q)x+pq
=x2+px+qx+pq
=(x+p)(x+q).
说理验证:
事实上,我们也可以用如下方法进行变形:
x2+(p+q)x+pq
=x2+px+qx+pq
=(x2+px)+(qx+pq)
=x(x+p)+q(x+p)
=(x+p)·(x+q).
于是,我们可以利用上面的方法进行多项式的因式分解.
尝试运用:
例题:把x2+3x+2因式分解.
解:x2+3x+2=x2+(2+1)x+2×1=(x+2)(x+1).
请利用上述方法将下列多项式因式分解.
(1)y2+6y+5;
解:原式=y2+(1+5)y+1×5
=(y+1)(y+5).
(2)x2-2x-8;
解:原式=x2+[2+(-4)]x+2×(-4)
=(x+2)(x-4).
(3)(y2+y)2+7(y2+y)-18.
解:原式=(y2+y)2+[9+(-2)](y2+y)+9×(-2)
=(y2+y+9)(y2+y-2)
=(y2+y+9)(y+2)(y-1).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
北师大版八年级数学下册 第四章 名校优选检测题
(满分120分,考试用时120分钟)
姓名:________ 班级:________ 分数:________
一、选择题(每小题3分,共30分)
1.下列等式中,从左到右的变形中是因式分解的是( )
A.9x2-6x+1=(3x-1)2 B.x2-4x+1=x(x-4)+1
C.3m(m-n)=3m2-3mn D.x+3y=(x+y)+2y
2.将多项式-6a3b2+2a2b2因式分解时,应提取的公因式是( )
A.-2a2b2 B.-2ab C.-2a2b D.-2a3b3
3.有下列各式:①x2+y2;②4x2-y2;③-x2-9y2;④-x2+y2;⑤x2-4xy+4y2;⑥m2-9m.其中可用平方差公式因式分解的有( )
A.1个 B.2个 C.3个 D.4个
4.在多项式①x2+xy-y2;②-x2+2xy-y2;③xy+x2+y2;④1-x+中,能用完全平方公式因式分解的是( )
A.①② B.①③ C.②④ D.①④
5.把多项式4a2b+4ab2+b3因式分解,正确的是( )
A.a(2a+b)2 B.b(2a+b)2 C.(a+2b)2 D.4b(a+b)2
6.若多项式x2+mx-28可因式分解为(x-4)(x+7),则m的值为( )
A.-3 B.11 C.-11 D.3
7.在边长为a的正方形中挖去一个边长为b的小正方形(a>b),再沿虚线剪开(如图①),然后拼成一个等腰梯形(如图②),根据这两个图形的面积关系,表明下列式子中成立的是( )
A.a2-b2=(a+b)(a-b) B.(a+b)2=a2+2ab+b2
C.(a-b)2=a2-2ab+b2 D.a2-b2=(a-b)2
8.对于任意整数m,多项式(4m-5)2-9都能被下列选项整除的是( )
A.8 B.m C.m-1 D.m+2
9.小强是一位密码编译爱好者,在他的密码手册中,有这样一条信息:a-b,x-y,x+y,a+b,x2-y2,a2-b2分别对应下列六个字:家,爱,我,乡,游,美,现将(x2-y2)a2-(x2-y2)b2因式分解,结果呈现的密码信息可能是( )
A.我爱美 B.家乡游 C.爱我家乡 D.美我家乡
10.一个三角形的两边长为x,y,且使x3+x2y-xy2-y3=0,则此三角形的形状按边分一定为( )
A.等腰三角形 B.等边三角形 C.不等边三角形 D.无法判断
二、填空题(每小题3分,共24分)
11.(x+3)(2x-1)是多项式 因式分解的结果.
12.请在二项式x2-□y2的□里面添加一个式子,使其能因式分解,在“□”中添加的式子是 (写出一个即可).
13.(宜宾中考)分解因式:xy2-4x= .
14.(苏州中考)若a+b=4,a-b=1,则(a+1)2-(b-1)2的值为 .
15.甲、乙两同学因式分解x2+mx+n,甲看错了n,分解结果为(x+2)(x+4);乙看错了m,分解结果为(x+1)(x+9),则正确的因式分解结果是 .
在一个边长为12.75 cm的正方形内挖去一个边长为7.25 cm的正方形,则剩下部分的面积为 cm2.
17.已知a,b,c为△ABC的三边,试判断(a+b)2-c2的值 (选填“大于”“小于”或“等于”)零.
18.阅读下列文字与例题:
将一个多项式分组后,可提公因式或运用公式继续分解的方法是分组分解法.
例如:(1)am+an+bm+bn=(am+bm)+(an+bn)=m(a+b)+n(a+b)=(a+b)(m+n).
(2)x2-y2-2y-1=x2-(y2+2y+1)=x2-(y+1)2=(x+y+1)(x-y-1).
试用上述方法因式分解a2+2ab+ac+bc+b2= .
三、解答题(共66分)
19.(8分)分解因式:
(1)6x3-24x; (2)(a+b)2-4(a+b-1).
20.(10分)利用分解因式方法简便计算:40×3.52+80×3.5×1.5+40×1.52.
21.(12分)先分解因式,再计算求值.
(1)已知a-b=5,ab=3,求代数式a3b-a2b2+ab3的值;
(2)(2x-3y)2-(2x+3y)2,其中x=,y=.
22.(12分)数学知识奥妙无穷,小玉观察下面的算式:
72-12=48=12×4;
82-22=60=12×5;
92-32=72=12×6;
102-42=84=12×7;
…
从中惊奇地发现:这些算式均为12的倍数,但却不知其中的原因,她非常纳闷,请利用所学的知识给小玉解释一下.
23.(12分)小刚碰到一道题目:“分解因式x2+2x-3”,不会做,去问老师,老师说:“能否变成平方差的形式?把原式加上1,再减去1,这样原式化为(x2+2x+1)-4,…”,老师话没讲完,小刚就恍然大悟,他马上就做好了此题.
(1)请完成他因式分解的步骤;
(2)运用这种方法因式分解:a2-2ab-3b2.
24.(12分)观察猜想:
如图,大长方形是由四个小长方形拼成的,请根据此图填空:
x2+(p+q)x+pq
=x2+px+qx+pq
=( )( ).
说理验证:
事实上,我们也可以用如下方法进行变形:
x2+(p+q)x+pq
=x2+px+qx+pq
=(x2+px)+(qx+pq)
= .
=( )·( ).
于是,我们可以利用上面的方法进行多项式的因式分解.
尝试运用:
例题:把x2+3x+2因式分解.
解:x2+3x+2=x2+(2+1)x+2×1=(x+2)(x+1).
请利用上述方法将下列多项式因式分解.
(1)y2+6y+5;
(2)x2-2x-8;
(3)(y2+y)2+7(y2+y)-18.
参考答案
一、选择题(每小题3分,共30分)
1.下列等式中,从左到右的变形中是因式分解的是(A)
A.9x2-6x+1=(3x-1)2 B.x2-4x+1=x(x-4)+1
C.3m(m-n)=3m2-3mn D.x+3y=(x+y)+2y
2.将多项式-6a3b2+2a2b2因式分解时,应提取的公因式是(A)
A.-2a2b2 B.-2ab C.-2a2b D.-2a3b3
3.有下列各式:①x2+y2;②4x2-y2;③-x2-9y2;④-x2+y2;⑤x2-4xy+4y2;⑥m2-9m.其中可用平方差公式因式分解的有(B)
A.1个 B.2个 C.3个 D.4个
4.在多项式①x2+xy-y2;②-x2+2xy-y2;③xy+x2+y2;④1-x+中,能用完全平方公式因式分解的是(C)
A.①② B.①③ C.②④ D.①④
5.把多项式4a2b+4ab2+b3因式分解,正确的是(B)
A.a(2a+b)2 B.b(2a+b)2 C.(a+2b)2 D.4b(a+b)2
6.若多项式x2+mx-28可因式分解为(x-4)(x+7),则m的值为(D)
A.-3 B.11 C.-11 D.3
7.在边长为a的正方形中挖去一个边长为b的小正方形(a>b),再沿虚线剪开(如图①),然后拼成一个等腰梯形(如图②),根据这两个图形的面积关系,表明下列式子中成立的是(A)
A.a2-b2=(a+b)(a-b) B.(a+b)2=a2+2ab+b2
C.(a-b)2=a2-2ab+b2 D.a2-b2=(a-b)2
8.对于任意整数m,多项式(4m-5)2-9都能被下列选项整除的是(A)
A.8 B.m C.m-1 D.m+2
9.小强是一位密码编译爱好者,在他的密码手册中,有这样一条信息:a-b,x-y,x+y,a+b,x2-y2,a2-b2分别对应下列六个字:家,爱,我,乡,游,美,现将(x2-y2)a2-(x2-y2)b2因式分解,结果呈现的密码信息可能是(C)
A.我爱美 B.家乡游 C.爱我家乡 D.美我家乡
10.一个三角形的两边长为x,y,且使x3+x2y-xy2-y3=0,则此三角形的形状按边分一定为(A)
A.等腰三角形 B.等边三角形 C.不等边三角形 D.无法判断
二、填空题(每小题3分,共24分)
11.(x+3)(2x-1)是多项式2x2+5x-3因式分解的结果.
12.请在二项式x2-□y2的□里面添加一个式子,使其能因式分解,在“□”中添加的式子是4(答案不唯一)(写出一个即可).
13.(宜宾中考)分解因式:xy2-4x=x(y+2)(y-2).
14.(苏州中考)若a+b=4,a-b=1,则(a+1)2-(b-1)2的值为12.
15.甲、乙两同学因式分解x2+mx+n,甲看错了n,分解结果为(x+2)(x+4);乙看错了m,分解结果为(x+1)(x+9),则正确的因式分解结果是(x+3)2.
在一个边长为12.75 cm的正方形内挖去一个边长为7.25 cm的正方形,则剩下部分的面积为110 cm2.
17.已知a,b,c为△ABC的三边,试判断(a+b)2-c2的值大于(选填“大于”“小于”或“等于”)零.
18.阅读下列文字与例题:
将一个多项式分组后,可提公因式或运用公式继续分解的方法是分组分解法.
例如:(1)am+an+bm+bn=(am+bm)+(an+bn)=m(a+b)+n(a+b)=(a+b)(m+n).
(2)x2-y2-2y-1=x2-(y2+2y+1)=x2-(y+1)2=(x+y+1)(x-y-1).
试用上述方法因式分解a2+2ab+ac+bc+b2=(a+b)(a+b+c).
三、解答题(共66分)
19.(8分)分解因式:
(1)6x3-24x;
解:原式=6x(x2-4)
=6x(x+2)(x-2).
(2)(a+b)2-4(a+b-1).
解:原式=(a+b)2-4(a+b)+4
=(a+b-2)2.
20.(10分)利用分解因式方法简便计算:40×3.52+80×3.5×1.5+40×1.52.
解:40×3.52+80×3.5×1.5+40×1.52
=40×(3.5+1.5)2
=40×52
=1 000.
21.(12分)先分解因式,再计算求值.
(1)已知a-b=5,ab=3,求代数式a3b-a2b2+ab3的值;
解:∵a3b-a2b2+ab3=ab(a2-2ab+b2)
=ab(a-b)2,
而ab=3,a-b=5,
∴原式=×3×52=.
(2)(2x-3y)2-(2x+3y)2,其中x=,y=.
解: (2x-3y)2-(2x+3y)2
=(2x-3y+2x+3y)(2x-3y-2x-3y)
=4x·(-6y)
=-24xy,
把x=,y=代入得
原式=-24××=-.
22.(12分)数学知识奥妙无穷,小玉观察下面的算式:
72-12=48=12×4;
82-22=60=12×5;
92-32=72=12×6;
102-42=84=12×7;
…
从中惊奇地发现:这些算式均为12的倍数,但却不知其中的原因,她非常纳闷,请利用所学的知识给小玉解释一下.
解:根据上述规律可知,第n个式子左边可表示为(n+6)2-n2,
∴(n+6)2-n2=(n+6+n)(n+6-n)=2(n+3)·6=12(n+3).
∵n为正整数,∴(n+6)2-n2是12的倍数.
23.(12分)小刚碰到一道题目:“分解因式x2+2x-3”,不会做,去问老师,老师说:“能否变成平方差的形式?把原式加上1,再减去1,这样原式化为(x2+2x+1)-4,…”,老师话没讲完,小刚就恍然大悟,他马上就做好了此题.
(1)请完成他因式分解的步骤;
(2)运用这种方法因式分解:a2-2ab-3b2.
解:(1)x2+2x-3=(x2+2x+1)-4
=(x+1)2-22
=(x+1+2)(x+1-2)
=(x+3)(x-1).
(2)a2-2ab-3b2=a2-2ab+b2-4b2
=(a-b)2-4b2
=(a-b+2b)(a-b-2b)
=(a+b)(a-3b).
24.(12分)观察猜想:
如图,大长方形是由四个小长方形拼成的,请根据此图填空:
x2+(p+q)x+pq
=x2+px+qx+pq
=(x+p)(x+q).
说理验证:
事实上,我们也可以用如下方法进行变形:
x2+(p+q)x+pq
=x2+px+qx+pq
=(x2+px)+(qx+pq)
=x(x+p)+q(x+p)
=(x+p)·(x+q).
于是,我们可以利用上面的方法进行多项式的因式分解.
尝试运用:
例题:把x2+3x+2因式分解.
解:x2+3x+2=x2+(2+1)x+2×1=(x+2)(x+1).
请利用上述方法将下列多项式因式分解.
(1)y2+6y+5;
解:原式=y2+(1+5)y+1×5
=(y+1)(y+5).
(2)x2-2x-8;
解:原式=x2+[2+(-4)]x+2×(-4)
=(x+2)(x-4).
(3)(y2+y)2+7(y2+y)-18.
解:原式=(y2+y)2+[9+(-2)](y2+y)+9×(-2)
=(y2+y+9)(y2+y-2)
=(y2+y+9)(y+2)(y-1).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
