4.3.2 角的比较与运算(2)
文档属性
| 名称 | 4.3.2 角的比较与运算(2) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-04 00:00:00 | ||
图片预览




文档简介
课件15张PPT。4.3 角(第4课时)
4.3.2 角的比较与运算(2)本节课主要学习角的运算与角平分线的运用. 学习目标: 1. 进一步理解角的和差、角平分线的几何意义及数量关系,并会用图形语言、文字语言、符号语言进行综合描述。 2. 经历探究角的和差、角平分线的运用过程,体会数形结合思想.学习重点:
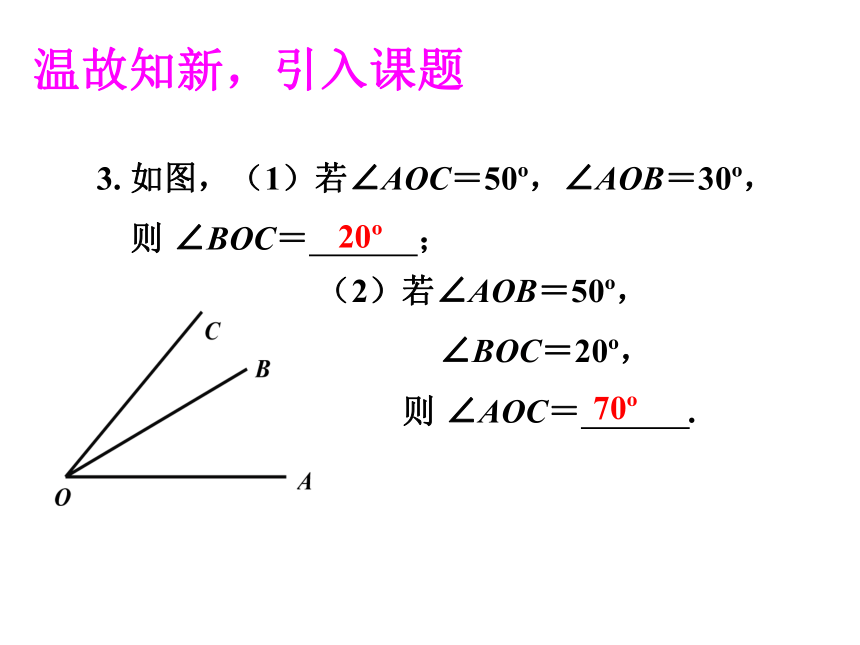
用图形语言、文字语言、符号语言综合描述角的和差关系及角平分线,并能够解决。温故知新,引入课题1.直角的度数为多少?平角呢?周角呢?2.角的度量单位:度、分、秒之间的换算是以多少为进制的?90°,180°,360°.603. 如图,(1)若∠AOC=50o,∠AOB=30o,
则 ∠BOC= ;温故知新,引入课题(2)若∠AOB=50o,
∠BOC=20o,
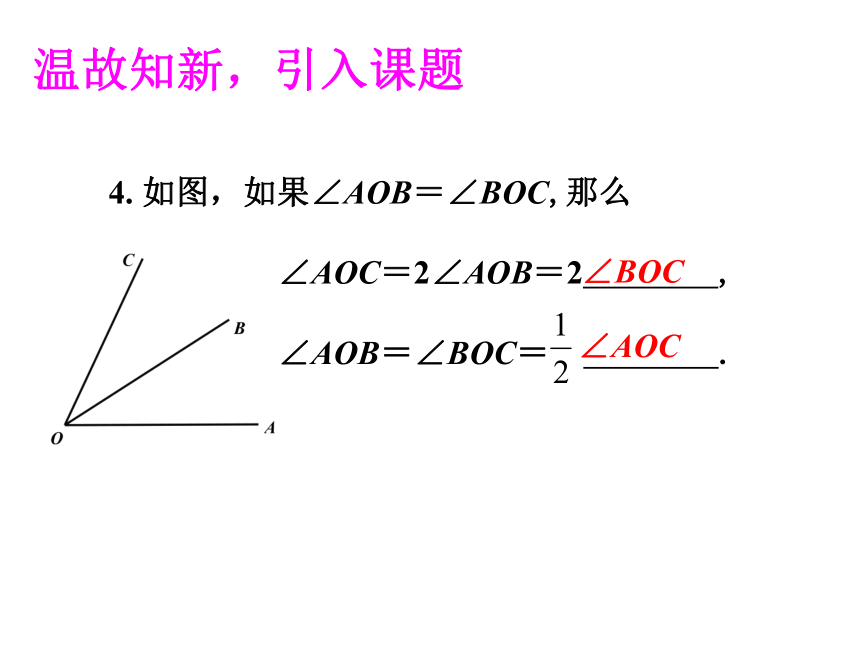
则 ∠AOC= .20o70o4. 如图,如果∠AOB=∠BOC,那么
∠AOC=2∠AOB=2 ,
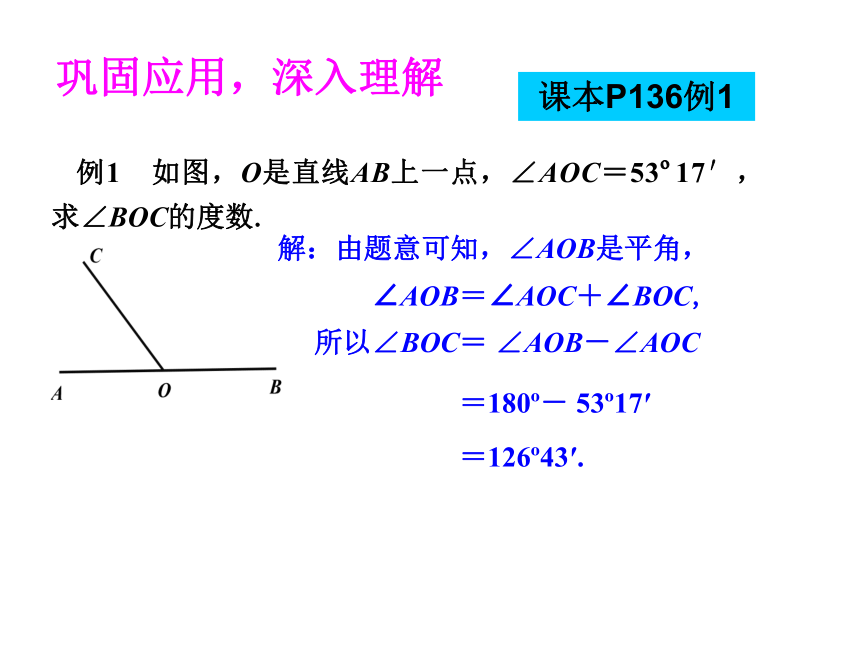
∠AOB=∠BOC= .温故知新,引入课题∠BOC ∠AOC巩固应用,深入理解解:由题意可知,∠AOB是平角,∠AOB=∠AOC+∠BOC,所以∠BOC= ∠AOB-∠AOC=180o- 53o17′=126o43′.课本P136例1巩固应用,深入理解解:360o÷7=51o+3o÷7=51o+180′÷7≈51o26′.答:每份是51o26′.课本P136例2巩固应用,深入理解解:由题意可知,∠AOB=∠AOC+∠BOC,所以∠AOC=∠AOB-∠BOC=90o- 60o=30o.由OD是∠AOC的平分线可知,∠COD= ∠AOC= ×30o
= 15o.所以∠BOD=∠COD+∠BOC
=15o +60o
=75o.
练一练1.如图,把一个蛋糕等分成8份,每份中的角是多少度?如果要使每份中的角是15o,这个蛋糕应等分成多少份?解:360o÷8=45o , 答:蛋糕等分成8份,每份中的角是45o;要使每份中的角是15o,这个蛋糕应等分成24份.
360o÷15o=24 .课本P136练习第2题练一练2.如图,O是直线AB上一点, OC是∠AOB的平分线, ∠COD=31o28′,求∠AOD的度数.解:由题意可知,∠AOB是平角,由OC是∠AOB的平分线可知,∠AOC= ∠AOB= ×180°
= 90o.由∠AOC=∠AOD+∠COD可知,∠AOD=∠AOC-∠COD=90o-31o28′ =58o32′. 课本P136练习第3题3. 如图,已知∠DOE=70o,∠DOB=40o,OD平分∠AOB,OE平分∠BOC,求∠AOC. 解:由题意可知,
∠DOE=∠DOB+∠BOE,所以∠BOE=∠DOE-∠DOB=70o-40o=30o.由OD平分∠AOB, OE平分∠BOC可知,∠AOB=2∠DOB=2 × 40o=80o,∠BOC=2∠BOE=2×30o=70o.所以∠AOC=∠AOB+∠BOC=80o+70o=150 o. 本题中如果去掉“∠DOB=40o”的条件,还能求出∠AOC的度数吗?练一练3.如图,已知∠DOE=70o,∠DOB=40o, OD平分∠AOB, OE平分∠BOC,求∠AOC. 解:由OD平分∠AOB,
OE平分∠BOC可知,∠AOB=2∠DOB,∠BOC=2∠BOE,所以∠AOC=∠AOB+∠BOC=2∠DOB+2∠BOE =2(∠DOB+∠BOE) =2∠DOE =2 × 70o=140o.今天你学到了哪些知识?小结与回顾1、角的和、差、倍、分的计算。学会了60进制的换算方法。
2、明确了角平分线的几何意义,并利用角平分线的概念计算角的大小。
3、需要注意的是数形结合的思想方法。作业:
1. 教科书习题4.3第10题.2.(选做题)已知∠AOB=90°,∠BOC=60°,OD是∠AOC的平分线,求∠BOD的度数.(提示:画图时要分情况讨论.)3.(选做题)(1)如图,已知∠AOB=90o,∠AOC=60o, OD平分∠BOC, OE平分∠AOC,求∠DOE.
(2)在上题中若∠AOC是
任意一个锐角,其他条
件不变,你还能求出
∠DOE的度数吗?说出
你的理由.
4.3.2 角的比较与运算(2)本节课主要学习角的运算与角平分线的运用. 学习目标: 1. 进一步理解角的和差、角平分线的几何意义及数量关系,并会用图形语言、文字语言、符号语言进行综合描述。 2. 经历探究角的和差、角平分线的运用过程,体会数形结合思想.学习重点:
用图形语言、文字语言、符号语言综合描述角的和差关系及角平分线,并能够解决。温故知新,引入课题1.直角的度数为多少?平角呢?周角呢?2.角的度量单位:度、分、秒之间的换算是以多少为进制的?90°,180°,360°.603. 如图,(1)若∠AOC=50o,∠AOB=30o,
则 ∠BOC= ;温故知新,引入课题(2)若∠AOB=50o,
∠BOC=20o,
则 ∠AOC= .20o70o4. 如图,如果∠AOB=∠BOC,那么
∠AOC=2∠AOB=2 ,
∠AOB=∠BOC= .温故知新,引入课题∠BOC ∠AOC巩固应用,深入理解解:由题意可知,∠AOB是平角,∠AOB=∠AOC+∠BOC,所以∠BOC= ∠AOB-∠AOC=180o- 53o17′=126o43′.课本P136例1巩固应用,深入理解解:360o÷7=51o+3o÷7=51o+180′÷7≈51o26′.答:每份是51o26′.课本P136例2巩固应用,深入理解解:由题意可知,∠AOB=∠AOC+∠BOC,所以∠AOC=∠AOB-∠BOC=90o- 60o=30o.由OD是∠AOC的平分线可知,∠COD= ∠AOC= ×30o
= 15o.所以∠BOD=∠COD+∠BOC
=15o +60o
=75o.
练一练1.如图,把一个蛋糕等分成8份,每份中的角是多少度?如果要使每份中的角是15o,这个蛋糕应等分成多少份?解:360o÷8=45o , 答:蛋糕等分成8份,每份中的角是45o;要使每份中的角是15o,这个蛋糕应等分成24份.
360o÷15o=24 .课本P136练习第2题练一练2.如图,O是直线AB上一点, OC是∠AOB的平分线, ∠COD=31o28′,求∠AOD的度数.解:由题意可知,∠AOB是平角,由OC是∠AOB的平分线可知,∠AOC= ∠AOB= ×180°
= 90o.由∠AOC=∠AOD+∠COD可知,∠AOD=∠AOC-∠COD=90o-31o28′ =58o32′. 课本P136练习第3题3. 如图,已知∠DOE=70o,∠DOB=40o,OD平分∠AOB,OE平分∠BOC,求∠AOC. 解:由题意可知,
∠DOE=∠DOB+∠BOE,所以∠BOE=∠DOE-∠DOB=70o-40o=30o.由OD平分∠AOB, OE平分∠BOC可知,∠AOB=2∠DOB=2 × 40o=80o,∠BOC=2∠BOE=2×30o=70o.所以∠AOC=∠AOB+∠BOC=80o+70o=150 o. 本题中如果去掉“∠DOB=40o”的条件,还能求出∠AOC的度数吗?练一练3.如图,已知∠DOE=70o,∠DOB=40o, OD平分∠AOB, OE平分∠BOC,求∠AOC. 解:由OD平分∠AOB,
OE平分∠BOC可知,∠AOB=2∠DOB,∠BOC=2∠BOE,所以∠AOC=∠AOB+∠BOC=2∠DOB+2∠BOE =2(∠DOB+∠BOE) =2∠DOE =2 × 70o=140o.今天你学到了哪些知识?小结与回顾1、角的和、差、倍、分的计算。学会了60进制的换算方法。
2、明确了角平分线的几何意义,并利用角平分线的概念计算角的大小。
3、需要注意的是数形结合的思想方法。作业:
1. 教科书习题4.3第10题.2.(选做题)已知∠AOB=90°,∠BOC=60°,OD是∠AOC的平分线,求∠BOD的度数.(提示:画图时要分情况讨论.)3.(选做题)(1)如图,已知∠AOB=90o,∠AOC=60o, OD平分∠BOC, OE平分∠AOC,求∠DOE.
(2)在上题中若∠AOC是
任意一个锐角,其他条
件不变,你还能求出
∠DOE的度数吗?说出
你的理由.
