角的概念推广
图片预览








文档简介
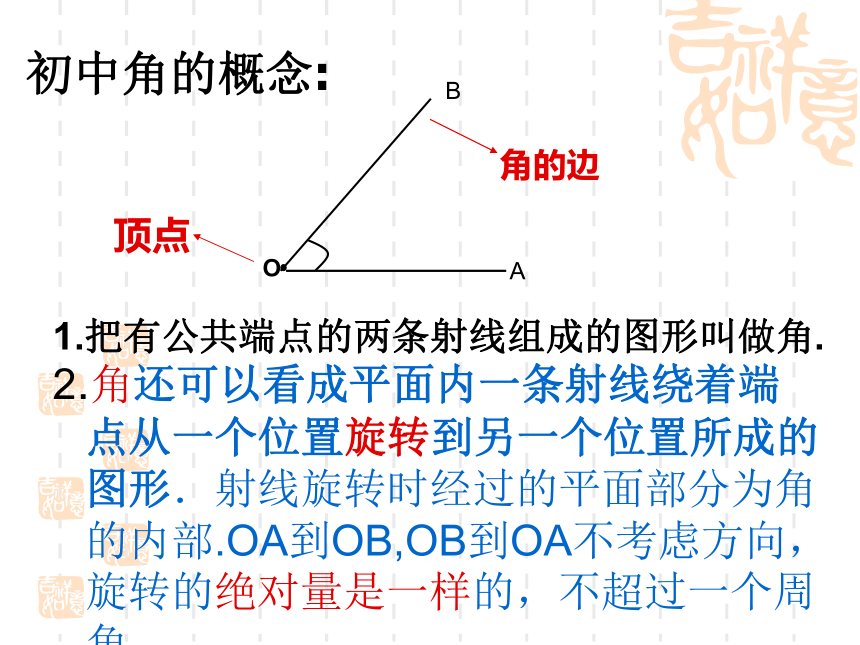
课件31张PPT。1.1.1角的概念的推广初中角的概念:1.把有公共端点的两条射线组成的图形叫做角.OA2.角还可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形.射线旋转时经过的平面部分为角的内部.OA到OB,OB到OA不考虑方向,旋转的绝对量是一样的,不超过一个周角.顶点角的边B1.教材例子:父母站在缆车两侧,观察缆车运行情况;2.体操:转体720°,转体3周; 跳水:翻腾两周半. 逆时针 顺时针拧松拧紧3.生活中的例子:31269快了慢了逆时针顺时针3.生活中的例子:小结:以上例子说明,生活需要,角度不应该只限于?并且角度应该考虑到?所以需要我们将初中学到的角的概念进行推广.一.正角、负角、零角:正角:一条射线绕着它的端点按逆时
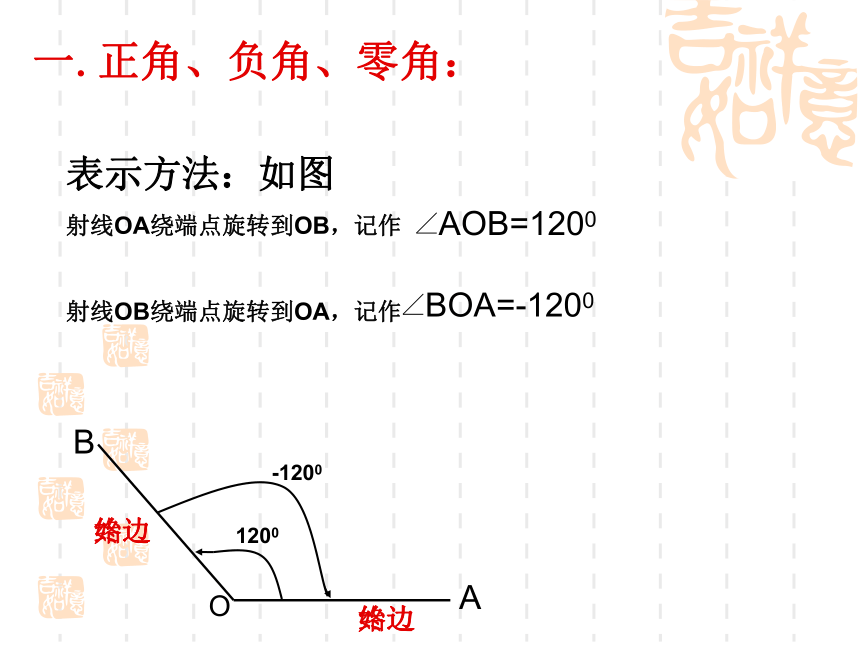
针方向旋转形成的角;负角:按顺时针方向旋转形成的角。零角:射线没有作任何旋转。说明1:旋转的绝对量是任意的; 说明2:用带箭头的弧来表示旋转的方向和旋转 的绝对量。旋转生成的角又称转角;说明3:经过推广,角可以是任意大小. 一.正角、负角、零角:始边终边始边终边表示方法:如图
射线OA绕端点旋转到OB,记作
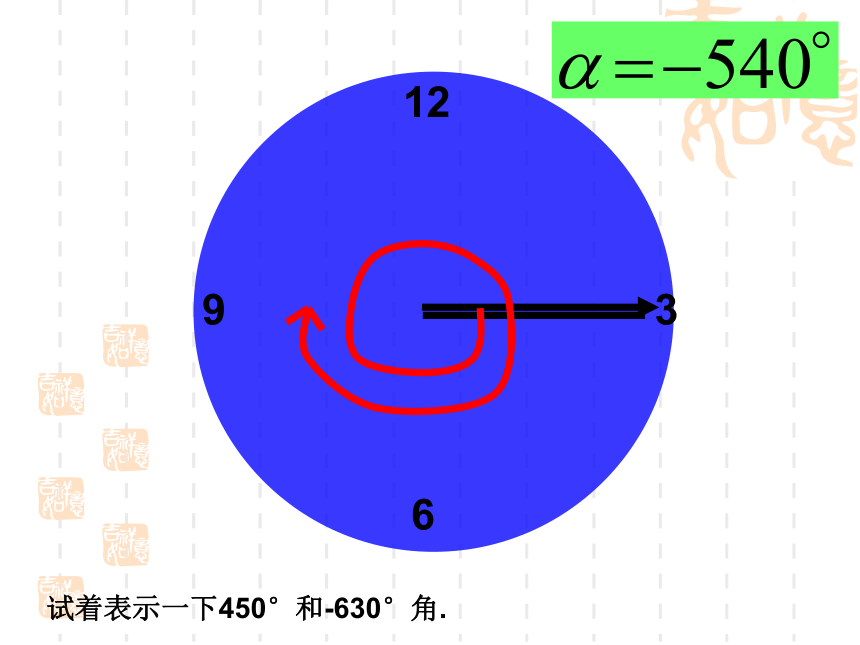
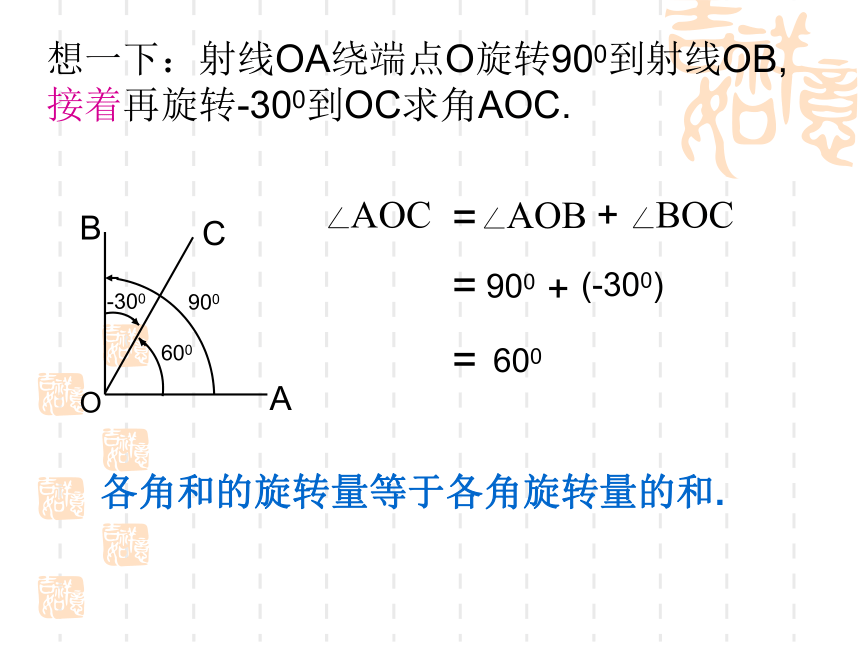
射线OB绕端点旋转到OA,记作31269OAB31269试着表示一下450°和-630°角.各角和的旋转量等于各角旋转量的和.想一下:射线OA绕端点O旋转900到射线OB, 接着再旋转-300到OC求角AOC.600==900+(-300)=600例 题 1:二.象限角: 角的顶点与坐标原点重合,角的始边
与x轴的正半轴重合,那角的终边在第
几象限,就说这个角是第几象限角.o注:当角的终边落在坐标轴上时,它不属于任何象限.它叫轴线角.角的概念推广以后:
从数值上看分为正角,负角,零角;
从终边位置上看分为象限角和轴线角.例2、作出下列各角并判断它们分 别是第几象限的角:
(1) 70°
(2) 210 °
(3) -60°OXY 70°第一象限角哦!OXY 210 °第三象限角哦!OXY -60°第四象限角哦!口答:说出以下角各属于第几象限:小组讨论:观察第(2)题各角有何特点?能否把(2)题这些角用一个集合表示出来呢?是不是任意一个角都与00到3600内的某一
角终边相同呢?3900-33003900=300+3600 -3300=300-3600=300+1x3600 =300 -1x3600 300 =300+0x3600 300+2x3600 , 300-2x3600 300+3x3600 , 300-3x3600 … , … ,与300终边相同的角的一般形式为300+K·3600,K ∈ Z问:观察
各角间关系?能否这些角用一个集合表示出来呢?思考:是不是任意一个角都与00到3600内的某一角 终边相同呢?结论:与300终边相同的角的一般形式为
300+K·3600,K ∈ Z三.终边相同角的表示方法: 所有与角 终边相同的角,连同角
在内可构成一个集合 即任意与角 终边相同的角,都可
以表示成 与整数个周角的和.终边相同的角不一定相等,
但相等的角终边一定相同,
终边相同的角有无数多个,
它们相差360°的整数倍
例3、 不作图判断下列各角是第几象 限的角: 585 ° -950 °585 °= 225°+ 1x360°-950 °= 130 °-3 x360°终边相同,第三象限角终边相同,第二象限角【例4】 在 00~3600 间,找出与下列各角终边相同的(1) ;(2) ;角,并判定它们是第几象限角. 例5 写出与600角终边相同角的集合S,
并把S中适合不等式-3600≤β<7200的
元素β写出来.解 S ={β| β=600+K?3600,K∈Z}S 中适合-3600≤β<7200的元素是:600-1x3600=-3000600+0x3600=600600+1x3600=4200巩固练习:5、小于90°的角都是锐角2、锐角是第一象限的角。 3、第一象限的角都是锐角。一、判断正误1、终边相同的角一定相等( )( )( )4、第二象限角一定比第一象限角大( )( )(2).在直角坐标系中,判断①.第一象限的角的一定是锐角;②.终边相同的角一定相等;③.相等的角终边一定相同;④.小于900的角一定是锐角;⑤.象限角为钝角的终边在第二象限;错对错错对二 、填空(第一个空填0°到360°间的角, 第二个 空填整数)并判断角所在的象限。
1) 640°= ______ + ___ x 360°, 640°是第___象限角
2) -120°= ______ + ___ x 360°, -120 °是第___象限角
3) 2008 °= ______ + ___ x 360°, 2008°是第___象限角 四三三小 结例6:思 考:1.如果 是第一象限角,那么 的取值
范围可以表示为怎样的不等式?2.如果 是第一象限角,那么 是第几
象限角?
针方向旋转形成的角;负角:按顺时针方向旋转形成的角。零角:射线没有作任何旋转。说明1:旋转的绝对量是任意的; 说明2:用带箭头的弧来表示旋转的方向和旋转 的绝对量。旋转生成的角又称转角;说明3:经过推广,角可以是任意大小. 一.正角、负角、零角:始边终边始边终边表示方法:如图
射线OA绕端点旋转到OB,记作
射线OB绕端点旋转到OA,记作31269OAB31269试着表示一下450°和-630°角.各角和的旋转量等于各角旋转量的和.想一下:射线OA绕端点O旋转900到射线OB, 接着再旋转-300到OC求角AOC.600==900+(-300)=600例 题 1:二.象限角: 角的顶点与坐标原点重合,角的始边
与x轴的正半轴重合,那角的终边在第
几象限,就说这个角是第几象限角.o注:当角的终边落在坐标轴上时,它不属于任何象限.它叫轴线角.角的概念推广以后:
从数值上看分为正角,负角,零角;
从终边位置上看分为象限角和轴线角.例2、作出下列各角并判断它们分 别是第几象限的角:
(1) 70°
(2) 210 °
(3) -60°OXY 70°第一象限角哦!OXY 210 °第三象限角哦!OXY -60°第四象限角哦!口答:说出以下角各属于第几象限:小组讨论:观察第(2)题各角有何特点?能否把(2)题这些角用一个集合表示出来呢?是不是任意一个角都与00到3600内的某一
角终边相同呢?3900-33003900=300+3600 -3300=300-3600=300+1x3600 =300 -1x3600 300 =300+0x3600 300+2x3600 , 300-2x3600 300+3x3600 , 300-3x3600 … , … ,与300终边相同的角的一般形式为300+K·3600,K ∈ Z问:观察
各角间关系?能否这些角用一个集合表示出来呢?思考:是不是任意一个角都与00到3600内的某一角 终边相同呢?结论:与300终边相同的角的一般形式为
300+K·3600,K ∈ Z三.终边相同角的表示方法: 所有与角 终边相同的角,连同角
在内可构成一个集合 即任意与角 终边相同的角,都可
以表示成 与整数个周角的和.终边相同的角不一定相等,
但相等的角终边一定相同,
终边相同的角有无数多个,
它们相差360°的整数倍
例3、 不作图判断下列各角是第几象 限的角: 585 ° -950 °585 °= 225°+ 1x360°-950 °= 130 °-3 x360°终边相同,第三象限角终边相同,第二象限角【例4】 在 00~3600 间,找出与下列各角终边相同的(1) ;(2) ;角,并判定它们是第几象限角. 例5 写出与600角终边相同角的集合S,
并把S中适合不等式-3600≤β<7200的
元素β写出来.解 S ={β| β=600+K?3600,K∈Z}S 中适合-3600≤β<7200的元素是:600-1x3600=-3000600+0x3600=600600+1x3600=4200巩固练习:5、小于90°的角都是锐角2、锐角是第一象限的角。 3、第一象限的角都是锐角。一、判断正误1、终边相同的角一定相等( )( )( )4、第二象限角一定比第一象限角大( )( )(2).在直角坐标系中,判断①.第一象限的角的一定是锐角;②.终边相同的角一定相等;③.相等的角终边一定相同;④.小于900的角一定是锐角;⑤.象限角为钝角的终边在第二象限;错对错错对二 、填空(第一个空填0°到360°间的角, 第二个 空填整数)并判断角所在的象限。
1) 640°= ______ + ___ x 360°, 640°是第___象限角
2) -120°= ______ + ___ x 360°, -120 °是第___象限角
3) 2008 °= ______ + ___ x 360°, 2008°是第___象限角 四三三小 结例6:思 考:1.如果 是第一象限角,那么 的取值
范围可以表示为怎样的不等式?2.如果 是第一象限角,那么 是第几
象限角?
