第18章平行四边形(基础篇)单元测试卷(含解析)
文档属性
| 名称 | 第18章平行四边形(基础篇)单元测试卷(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 723.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-19 11:27:30 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第18章 平行四边形(基础篇)
一、单选题(本大题共12小题,每小题3分,共36分)
1.下列∠A:∠B:∠C:∠D的值中,能判定四边形ABCD是平行四边形的是( )
A.1:2:3:4 B.1:4:2:3
C.1:2:2:1 D.3:2:3:2
2.如图,在 ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=5,则AE的长为( )
A.4 B.6 C.8 D.10
3.下列条件中不能判定四边形是平行四边形的是( )
A., B.,
C., D.,
4.如图,已知P、R分别是长方形ABCD的边BC、CD上的点,E、F分别是PA、PR的中点,点P在BC上从B向C移动,点R不动,那么下列结论成立的是( )
A.线段EF的长逐渐增大 B.线段EF的长逐渐变小
C.线段EF的长不变 D.无法确定
5.已知:如图,折叠矩形ABCD,使点B落在对角线AC上的点F处,若BC=8,AB=6,则线段CE的长度是( )
A.3 B.4 C.5 D.6
6.如图,在菱形ABCD中,AB=5,AC=6,过点D作DE⊥BA,交BA的延长线于点E,则线段DE的长为( )
A. B. C.4 D.
7.如图,四边形ABCD是正方形,延长AB到点E,使AE=AC,则∠BCE的度数是( )
A.22.5° B.25° C.23° D.20°
8.在四边形ABCD中,对角线AC,BD互相平分,要使四边形ABCD为矩形,需添加的条件是( )
A.∠B=90° B.∠A=∠C C.AB=BC D.AC⊥BD
9.如图,在平面直角坐标系中,以O(0,0),A(1,1),B(3,0)为顶点,构造平行四边形,下列各点中不能作为平行四边形顶点坐标的是( )
A.(-3,1) B.(4,1) C.(-2,1) D.(2,-1)
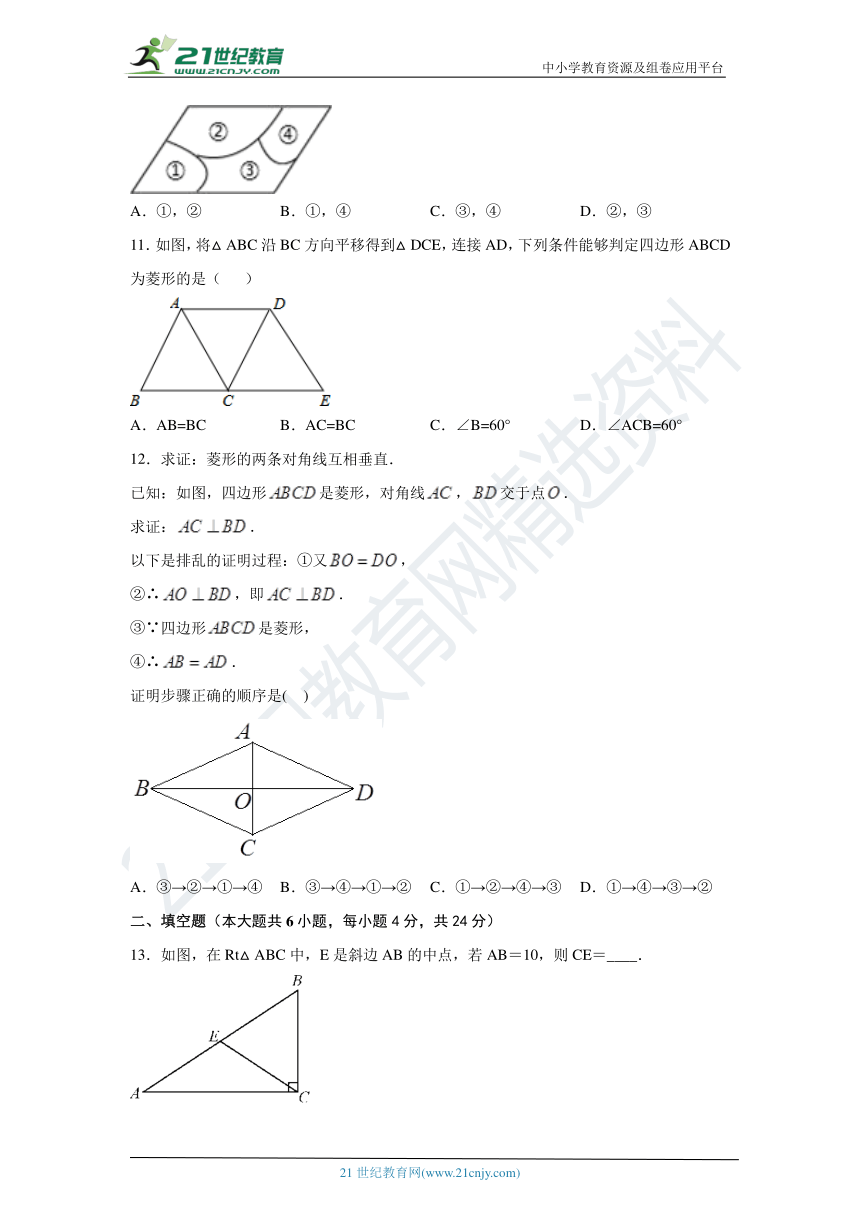
10.小敏不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带了两块碎玻璃,其编号应该是( )
A.①,② B.①,④ C.③,④ D.②,③
11.如图,将△ABC沿BC方向平移得到△DCE,连接AD,下列条件能够判定四边形ABCD为菱形的是( )
A.AB=BC B.AC=BC C.∠B=60° D.∠ACB=60°
12.求证:菱形的两条对角线互相垂直.
已知:如图,四边形是菱形,对角线,交于点.
求证:.
以下是排乱的证明过程:①又,
②∴,即.
③∵四边形是菱形,
④∴.
证明步骤正确的顺序是( )
A.③→②→①→④ B.③→④→①→② C.①→②→④→③ D.①→④→③→②
二、填空题(本大题共6小题,每小题4分,共24分)
13.如图,在Rt△ABC中,E是斜边AB的中点,若AB=10,则CE=____.
14.如图,在□ABCD中,BE平分∠ABC,BC=6,DE=2,则□ABCD的周长等于__________.
15.如图,在 ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=52°,∠DAE=20°,则∠FED′的大小为________.
16.如图,已知 OABC的顶点A、C分别在直线x=1和x=4上,O是坐标原点,则对角线OB长的最小值为__.
17.如图,的对角线与相交于点,按以下步骤作图:①以点为圆心,以任意长为半径作弧,分别交,于点,;②以点为圆心,以长为半径作弧,交于点;③以点为圆心,以长为半径作弧,在内部交前面的弧于点;④过点作射线交于点,若,则线段的长为_______.
18.如图,在△A1B1C1中,已知A1B1=7,B1C1=4,A1C1=5,依次连接△A1B1C1三边中点,得△A2B2C2,再依次连接△A2B2C2的三边中点得△A3B3C3,…,则△A5B5C5的周长为_________.
三、解答题(本大题共6小题,共60分)
19.(8分)如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E,
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.
20.(8分)如图,平行四边形中,,,、分别是、上的点,且,连接交于.
(1)求证:;
(2)若,延长交的延长线于,当,求的长.
21.(10分)如图,菱形ABCD的对角线AC、BD相交于点O,,,OE与AB交于点F.
(1)求证:四边形AEBO的为矩形;
(2)若OE=10,AC=16,求菱形ABCD的面积.
22.(10分)如图,已知平行四边形ABCD,若M,N是BD上两点,且BM=DN,AC=2OM,
(1)求证:四边形 AMCN 是矩形;
(2)△ABC 满足什么条件,四边形AMCN是正方形,请说明理由.
23.(12分)如图,点E、F、G、H分别在矩形ABCD的边AB、BC、CD、DA(不包括端点)上运动,且满足,.
(1)求证:;
(2)试判断四边形EFGH的形状,并说明理由.
(3)请探究四边形EFGH的周长一半与矩形ABCD一条对角线长的大小关系,并说明理由.
24.(12分)在正方形ABCD中,过点A引射线AH,交边CD于点H(点H与点D不重合).通过翻折,使点B落在射线AH上的点G处,折痕AE交BC于E,延长EG交CD于F.
【感知】如图1,当点H与点C重合时,可得FG=FD.
【探究】如图2,当点H为边CD上任意一点时,猜想FG与FD的数量关系,并说明理由.
【应用】在图2中,当AB=5,BE=3时,利用探究结论,求FG的长.
参考答案
1.D
【分析】两组对角分别相等的四边形是平行四边形,所以∠A和∠C是对角,∠B和∠D是对角,对角的份数应相等.
解:根据平行四边形的判定:两组对角分别相等的四边形是平行四边形,所以只有D符合条件.
故选:D.
【点拨】本题考查了平行四边形的判定,在应用判定定理判定平行四边形时,应仔细观察题目所给的条件,仔细选择适合于题目的判定方法进行解答,避免混用判定方法.
2.C
【分析】先证△ABO≌△AFO得到OB的长度,再用勾股定理求AO的长,再证△AOF≌△EOB,从而得到AE=2AO,即可求得AE的长.
解:设AG与BF交点为O,如图所示:
∵AB=AF,AG平分∠BAD,AO=AO,
∴△ABO≌△AFO,
∴BO=FO,∠AOB=∠AOF=90 ,
∵BF=6
∴BO=FO=BF=3
在Rt△AOB中,由勾股定理得:
,
在 ABCD中,AF∥BE,
∴∠FAO=∠BEO
又∵BO=FO,∠AOB=∠AOF
∴△AOF≌△EOB,
∴AO=EO,
∴AE=2AO=8,
故选C.
【点拨】本题考查全等三角形的判定和性质、平行四边形的性质、勾股定理及用尺规作图的方法画角平分线.
3.C
【分析】根据平行四边形的判断定理分别作出判断得出即可.
解:A.根据一组对边平行且相等的四边形是平行四边形,故选项正确,不符合题意;
B.根据平行四边形的定义:两组对边分别平行的四边形是平行四边形;故选项正确,不符合题意;
C.一组对边平行,另一组对边相等不能判断这个四边形是平行四边形,故选项错误,符合题意;
D. 如图,
∵AB∥CD,∴∠B+∠C=180°,
∵∠A=∠C,
∴∠A+∠B=180°,
∴AD∥BC,
∴四边形ABCD是平行四边形,
故选项正确,不符合题意;
故选:C.
【点拨】此题主要考查了平行四边形的判定定理,准确无误的掌握定理是解题关键.
4.C
【分析】因为R不动,所以AR不变.根据三角形中位线定理可得EF=AR,因此线段EF的长不变.
解:连接AR.
∵E、F分别是AP、RP的中点,
∴EF为△APR的中位线,
∴EF=AR,为定值.
∴线段EF的长不改变.
故选:C.
【点拨】本题考查了三角形的中位线定理,只要三角形的边AR不变,则对应的中位线的长度就不变.掌握三角形的中位线定理是解题关键.
5.C
【分析】在Rt△ABC中利用勾股定理可求出AC=10,设BE=a,则CE=8﹣a,根据折叠的性质可得出BE=FE=a,AF=AB=6,∠AFE=∠B=90°,进而可得出FC=4,在Rt△CEF中,利用勾股定理可得出关于a的一元二次方程,解之即可得出a值,将其代入8﹣a中即可得出线段CE的长度.
解:在Rt△ABC中,AB=6,BC=8,
∴AC=10.
设BE=a,则CE=8﹣a,
根据翻折的性质可知,BE=FE=a,AF=AB=6,∠AFE=∠B=90°,
∴FC=4.
在Rt△CEF中,EF=a,CE=8﹣a,CF=4,
∴CE2=EF2+CF2,即(8﹣a)2=a2+42,
解得:a=3,
∴8﹣a=5.
故选C.
【点拨】本题考查了翻折变换、矩形的性质、勾股定理以及解一元二次方程,在Rt△CEF中,利用勾股定理找出关于a的一元二次方程是解题的关键.
6.D
【分析】利用菱形的面积等于两对角线之积的一半,求解菱形的面积,再利用等面积法求菱形的高即可.
解:记AC与BD的交点为,
菱形,
菱形的面积
菱形的面积
故选D.
【点拨】本题考查的是菱形的性质,菱形的面积公式,勾股定理.理解菱形的对角线互相垂直平分和学会用等面积法是解题关键.
7.A
【分析】根据正方形的性质,易知∠CAE=∠ACB=45°;等腰△CAE中,根据三角形内角和定理可求得∠ACE的度数,进而可由∠BCE=∠ACE﹣∠ACB得出∠BCE的度数.
解:∵四边形ABCD是正方形,
∴∠CAB=∠BCA=45°;
△ACE中,AC=AE,
则:∠ACE=∠AEC=(180°﹣∠CAE)=67.5°;
∴∠BCE=∠ACE﹣∠ACB=22.5°.
考点:正方形的性质.
8.A
【分析】四边形ABCD的对角线互相平分,则说明四边形是平行四边形,由矩形的判定定理知,只需添加条件是对角线相等或有一内角为直角即可.
解:∵对角线AC与BD互相平分,
∴四边形ABCD是平行四边形,
∴要使四边形ABCD成为矩形,
需添加一个条件是:对角线相等(AC=BD)或有一个内角等于90°.
故选:A.
【点拨】本题考查了平行四边形的判定定理与矩形的判定定理.掌握对角线相等的平行四边形是矩形;有一个角是直角的平行四边形是矩形是解答本题的关键.
9.A
解:因为经过三点可构造三个平行四边形,即 AOBC1、 ABOC2、 AOC3B.根据平行四边形的性质,可知B、C、D正好是C1、C2、C3的坐标,
故选A.
10.D
【分析】确定有关平行四边形,关键是确定平行四边形的四个顶点,由此即可解决问题.
只有②③两块角的两边互相平行,且中间部分相联,角的两边的延长线的交点就是平行四边形的顶点,
∴带②③两块碎玻璃,就可以确定平行四边形的大小.
故选D.
【点拨】本题考查平行四边形的定义以及性质,解题的关键是理解如何确定平行四边形的四个顶点,四个顶点的位置确定了,平行四边形的大小就确定了,属于中考常考题型.
11.A
∵将△ABC沿BC方向平移得到△DCE,
∴ABCD,
∴四边形ABCD为平行四边形,
∴当AB=BC时,平行四边形ABCD是菱形,
故选A.
12.B
试题分析:根据菱形的性质,首先得到AB=AD和BO=DO,再根据等腰三角形的“三线合一”证明⊥BD,故答案选B.
考点:菱形的性质,等腰三角形的性质.
13.5
试题分析:根据直角三角形斜边上的中线等于斜边的一半,可得CE=AB=5.
考点:直角三角形斜边上的中线.
14.20
【分析】根据四边形ABCD为平行四边形可得AE∥BC,根据平行线的性质和角平分线的性质可得出∠ABE=∠AEB,继而可得AB=AE,然后根据已知可求得结果.
解:∵四边形ABCD为平行四边形,
∴AE∥BC,AD=BC,
∴∠AEB=∠EBC,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠ABE=∠AEB,
∴AB=AE,
∴AE+DE=AD=BC=6,
∴AE+2=6,
∴AE=4,
∴AB=CD=4,
∴ ABCD的周长=4+4+6+6=20,
故答案为20.
考点:平行四边形的性质.
15.36°
解:∵四边形ABCD是平行四边形,
∴∠D=∠B=52°,
由折叠的性质得:∠D′=∠D=52°,∠EAD′=∠DAE=20°,
∴∠AEF=∠D+∠DAE=52°+20°=72°,∠AED′=180°-∠EAD′-∠D′=108°,
∴∠FED′=108°-72°=36°;
故答案为36°.
【点拨】本题考查了平行四边形的性质、折叠的性质、三角形的外角性质以及三角形内角和定理;熟练掌握平行四边形的性质和折叠的性质,求出∠AEF和∠AED′是解决问题的关键.
16.5.
试题分析:当B在x轴上时,对角线OB长的最小,如图所示:直线x=1与x轴交于点D,直线x=4与x轴交于点E,根据题意得:∠ADO=∠CEB=90°,OD=1,OE=4,∵四边形ABCD是平行四边形,∴OA∥BC,OA=BC,∴∠AOD=∠CBE,在△AOD和△CBE中,∵∠AOD=∠CBE,∠ADO=∠CEB,OA=BC,∴△AOD≌△CBE(AAS),∴OD=BE=1,∴OB=OE+BE=5;故答案为5.
考点:平行四边形的性质;坐标与图形性质.
17.4.
【分析】连接和,根据全等三角形的判定与性质及中位数定理即可求解.
连接和,因为,,,所以,所以,,所以,又因为是中点,所以是△的中位线,所以,所以.
【点拨】此题主要考查平行四边形的性质,解题的关键是熟知全等三角形的判定与性质及中位线的应用.
18.1
试题分析:根据三角形的中位线定理得:A2B2、B2C2、C2A2分别等于A1B1、B1C1、C1A1的一半,所以△A2B2C2的周长等于△A1B1C1的周长的一半,以此类推可求出△A5B5C5的周长为△A1B1C1的周长的,则周长=(7+4+5)×=1.
考点:三角形中位线的性质.
19.(1)详见解析;(2).
试题分析:(1)由平行四边形的性质和角平分线易证∠BAE=∠BEA,根据等腰三角形的性质可得AB=BE;(2)易证△ABE是等边三角形,根据等边三角形的性质可得AE=AB=4,AF=EF=2,由勾股定理求出BF,再由AAS证明△ADF≌△ECF,即△ADF的面积=△ECF的面积,因此平行四边形ABCD的面积=△ABE的面积=AE BF,即可得出结果.
试题解析:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AB=CD,
∴∠B+∠C=180°,∠AEB=∠DAE,
∵AE是∠BAD的平分线,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴AB=BE,∴BE=CD;
(2)解:∵AB=BE,∠BEA=60°,
∴△ABE是等边三角形,
∴AE=AB=4,
∵BF⊥AE,
∴AF=EF=2,
∴BF=,
∵AD∥BC,
∴∠D=∠ECF,∠DAF=∠E,
在△ADF和△ECF中,
,
∴△ADF≌△ECF(AAS),
∴△ADF的面积=△ECF的面积,
∴平行四边形ABCD的面积=△ABE的面积=AE BF=×4×2=4.
考点:全等三角形的判定与性质;平行四边形的性质.
20.(1)详见解析;(2)3
【分析】(1)由平行四边形的性质和AAS证明△OBE≌△ODF,得出对应边相等即可;
(2)证出AE=GE,再证明DG=DO,得出OF=FG=1,即可得出结果.
解:(1)证明:∵四边形是平行四边形
∴
∴
在与中,
∵
∴
∴
(2)∵
∴
∵
∴
∴
∵
∴
∴
∴
∴
由(1)可知,
∴
∴.
【点拨】本题考查了平行四边形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质;熟练掌握平行四边形的性质,证明三角形全等是解决问题(1)的关键.
21.(1)见解析;(2)96
【分析】(1)根据菱形的性质结合已知条件即可得证;
(2)由(1)所得结合菱形的性质计算出、的长度,再计算面积即可.
解:(1)证明:∵,,
∴四边形AEBO为平行四边形,
又∵四边形ABCD为菱形,
∴,
∴,
∴平行四边形AEBO为矩形;
(2)∵四边形AEBO为矩形,
∴AB=OE=10,
又∵四边形ABCD为菱形,
∴AO=AC=8,
∴,
∴,
∴BD=2BO=12,
∴菱形ABCD的面积=.
【点拨】本题考查了矩形的判定,菱形的性质,勾股定理;掌握好相关的基础知识是解决本题的关键.
22.(1)证明见解析;(2)AB=BC
【分析】(1)由平行四边形的性质可知:OA=OC,OB=OD,再证明OM=ON即可证明四边形AMCN是平行四边形;
(2)当AB=BC时,四边形AMCN是正方形;根据四边形ABCD是平行四边形,AB=BC即可得出四边形ABCD是菱形,再由(1)可知四边形AMCN是矩形;从而得出结论;
(1)证明:四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵对角线BD上的两点M、N满足BM=DN,
∴OB-BM=OD-DN,即OM=ON,
∴四边形AMCN是平行四边形,
∴MN=2OM,
∵ AC=2OM,
∴MN=AC,
∴四边形AMCN是矩形;
(2)当AB=BC时,四边形AMCN是正方形;
∵AB=BC,四边形ABCD是平行四边形,
∴ 四边形ABCD是菱形,
∴ AC⊥BD,
∴AC⊥MN,
由(1)可知四边形ABCD是矩形,
∴四边形ABCD是正方形;
【点拨】本题考查了矩形的判定,平行四边形的判定与性质,正方形的判定,解题的关键是灵活运用所学知识解决问题;
23.(1)证明见解析;(2)四边形EFGH是平行四边形,理由见解析;(3)四边形EFGH的周长一半大于或者等于矩形ABCD一条对角线长度,理由见解析.
【分析】(1)根据全等三角形的判定定理SAS证得结论;
(2)由(1)中全等三角形的性质得到:EH=GF,同理可得FE=HG,即可得四边形EFGH是平行四边形;
(3)由 轴对称--最短路径问题得到:四边形EFGH的周长一半大于或等于矩形ABCD一条对角线长度.
解:(1)∵四边形ABCD是矩形,
∴.
∴在与中,,
∴;
(2)∵由(1)知,,则,同理证得,则,
∴四边形EFGH是平行四边形;
(3) 四边形EFGH的周长一半大于或等于矩形ABCD一条对角线长度.
理由如下:作G关于BC的对称点G′,连接EG′,可得EG′的长度就是EF+FG的最小值.
连接AC,
∵CG′=CG=AE,AB∥CG′,
∴四边形AEG′C为平行四边形,
∴EG′=AC.
在△EFG′中,∵EF+FG′≥EG′=AC,
∴四边形EFGH的周长一半大于或等于矩形ABCD一条对角线长度.
【点拨】考查了矩形的性质,全等三角形的判定与性质.灵活运用这些性质进行推理证明是本题的关键.
24.【探究】FG=FD;【应用】.
试题分析:【探究】连接AF,根据图形猜想FD=FG,由折叠的性质可得AB=AG=AD,再结合AF为△AGF和△ADF的公共边,从而证明△AGF≌△ADF,从而得出结论.
【应用】设FG=x,则FC=5-x,FE=3+x,在RT△ECF中利用勾股定理可求出x的值,进而可得出答案.
【探究】猜想FD=FG.
连接AF,
由折叠的性质可得AB=AG=AD,
在Rt△AGF和Rt△ADF中,
,
∴△AGF≌△ADF.
∴FG=FD;
【应用】设GF=,则CF=5-,则EF=+3
在△ECF中由勾股定理得,,解得
∴FG的长为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第18章 平行四边形(基础篇)
一、单选题(本大题共12小题,每小题3分,共36分)
1.下列∠A:∠B:∠C:∠D的值中,能判定四边形ABCD是平行四边形的是( )
A.1:2:3:4 B.1:4:2:3
C.1:2:2:1 D.3:2:3:2
2.如图,在 ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=5,则AE的长为( )
A.4 B.6 C.8 D.10
3.下列条件中不能判定四边形是平行四边形的是( )
A., B.,
C., D.,
4.如图,已知P、R分别是长方形ABCD的边BC、CD上的点,E、F分别是PA、PR的中点,点P在BC上从B向C移动,点R不动,那么下列结论成立的是( )
A.线段EF的长逐渐增大 B.线段EF的长逐渐变小
C.线段EF的长不变 D.无法确定
5.已知:如图,折叠矩形ABCD,使点B落在对角线AC上的点F处,若BC=8,AB=6,则线段CE的长度是( )
A.3 B.4 C.5 D.6
6.如图,在菱形ABCD中,AB=5,AC=6,过点D作DE⊥BA,交BA的延长线于点E,则线段DE的长为( )
A. B. C.4 D.
7.如图,四边形ABCD是正方形,延长AB到点E,使AE=AC,则∠BCE的度数是( )
A.22.5° B.25° C.23° D.20°
8.在四边形ABCD中,对角线AC,BD互相平分,要使四边形ABCD为矩形,需添加的条件是( )
A.∠B=90° B.∠A=∠C C.AB=BC D.AC⊥BD
9.如图,在平面直角坐标系中,以O(0,0),A(1,1),B(3,0)为顶点,构造平行四边形,下列各点中不能作为平行四边形顶点坐标的是( )
A.(-3,1) B.(4,1) C.(-2,1) D.(2,-1)
10.小敏不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带了两块碎玻璃,其编号应该是( )
A.①,② B.①,④ C.③,④ D.②,③
11.如图,将△ABC沿BC方向平移得到△DCE,连接AD,下列条件能够判定四边形ABCD为菱形的是( )
A.AB=BC B.AC=BC C.∠B=60° D.∠ACB=60°
12.求证:菱形的两条对角线互相垂直.
已知:如图,四边形是菱形,对角线,交于点.
求证:.
以下是排乱的证明过程:①又,
②∴,即.
③∵四边形是菱形,
④∴.
证明步骤正确的顺序是( )
A.③→②→①→④ B.③→④→①→② C.①→②→④→③ D.①→④→③→②
二、填空题(本大题共6小题,每小题4分,共24分)
13.如图,在Rt△ABC中,E是斜边AB的中点,若AB=10,则CE=____.
14.如图,在□ABCD中,BE平分∠ABC,BC=6,DE=2,则□ABCD的周长等于__________.
15.如图,在 ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=52°,∠DAE=20°,则∠FED′的大小为________.
16.如图,已知 OABC的顶点A、C分别在直线x=1和x=4上,O是坐标原点,则对角线OB长的最小值为__.
17.如图,的对角线与相交于点,按以下步骤作图:①以点为圆心,以任意长为半径作弧,分别交,于点,;②以点为圆心,以长为半径作弧,交于点;③以点为圆心,以长为半径作弧,在内部交前面的弧于点;④过点作射线交于点,若,则线段的长为_______.
18.如图,在△A1B1C1中,已知A1B1=7,B1C1=4,A1C1=5,依次连接△A1B1C1三边中点,得△A2B2C2,再依次连接△A2B2C2的三边中点得△A3B3C3,…,则△A5B5C5的周长为_________.
三、解答题(本大题共6小题,共60分)
19.(8分)如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E,
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.
20.(8分)如图,平行四边形中,,,、分别是、上的点,且,连接交于.
(1)求证:;
(2)若,延长交的延长线于,当,求的长.
21.(10分)如图,菱形ABCD的对角线AC、BD相交于点O,,,OE与AB交于点F.
(1)求证:四边形AEBO的为矩形;
(2)若OE=10,AC=16,求菱形ABCD的面积.
22.(10分)如图,已知平行四边形ABCD,若M,N是BD上两点,且BM=DN,AC=2OM,
(1)求证:四边形 AMCN 是矩形;
(2)△ABC 满足什么条件,四边形AMCN是正方形,请说明理由.
23.(12分)如图,点E、F、G、H分别在矩形ABCD的边AB、BC、CD、DA(不包括端点)上运动,且满足,.
(1)求证:;
(2)试判断四边形EFGH的形状,并说明理由.
(3)请探究四边形EFGH的周长一半与矩形ABCD一条对角线长的大小关系,并说明理由.
24.(12分)在正方形ABCD中,过点A引射线AH,交边CD于点H(点H与点D不重合).通过翻折,使点B落在射线AH上的点G处,折痕AE交BC于E,延长EG交CD于F.
【感知】如图1,当点H与点C重合时,可得FG=FD.
【探究】如图2,当点H为边CD上任意一点时,猜想FG与FD的数量关系,并说明理由.
【应用】在图2中,当AB=5,BE=3时,利用探究结论,求FG的长.
参考答案
1.D
【分析】两组对角分别相等的四边形是平行四边形,所以∠A和∠C是对角,∠B和∠D是对角,对角的份数应相等.
解:根据平行四边形的判定:两组对角分别相等的四边形是平行四边形,所以只有D符合条件.
故选:D.
【点拨】本题考查了平行四边形的判定,在应用判定定理判定平行四边形时,应仔细观察题目所给的条件,仔细选择适合于题目的判定方法进行解答,避免混用判定方法.
2.C
【分析】先证△ABO≌△AFO得到OB的长度,再用勾股定理求AO的长,再证△AOF≌△EOB,从而得到AE=2AO,即可求得AE的长.
解:设AG与BF交点为O,如图所示:
∵AB=AF,AG平分∠BAD,AO=AO,
∴△ABO≌△AFO,
∴BO=FO,∠AOB=∠AOF=90 ,
∵BF=6
∴BO=FO=BF=3
在Rt△AOB中,由勾股定理得:
,
在 ABCD中,AF∥BE,
∴∠FAO=∠BEO
又∵BO=FO,∠AOB=∠AOF
∴△AOF≌△EOB,
∴AO=EO,
∴AE=2AO=8,
故选C.
【点拨】本题考查全等三角形的判定和性质、平行四边形的性质、勾股定理及用尺规作图的方法画角平分线.
3.C
【分析】根据平行四边形的判断定理分别作出判断得出即可.
解:A.根据一组对边平行且相等的四边形是平行四边形,故选项正确,不符合题意;
B.根据平行四边形的定义:两组对边分别平行的四边形是平行四边形;故选项正确,不符合题意;
C.一组对边平行,另一组对边相等不能判断这个四边形是平行四边形,故选项错误,符合题意;
D. 如图,
∵AB∥CD,∴∠B+∠C=180°,
∵∠A=∠C,
∴∠A+∠B=180°,
∴AD∥BC,
∴四边形ABCD是平行四边形,
故选项正确,不符合题意;
故选:C.
【点拨】此题主要考查了平行四边形的判定定理,准确无误的掌握定理是解题关键.
4.C
【分析】因为R不动,所以AR不变.根据三角形中位线定理可得EF=AR,因此线段EF的长不变.
解:连接AR.
∵E、F分别是AP、RP的中点,
∴EF为△APR的中位线,
∴EF=AR,为定值.
∴线段EF的长不改变.
故选:C.
【点拨】本题考查了三角形的中位线定理,只要三角形的边AR不变,则对应的中位线的长度就不变.掌握三角形的中位线定理是解题关键.
5.C
【分析】在Rt△ABC中利用勾股定理可求出AC=10,设BE=a,则CE=8﹣a,根据折叠的性质可得出BE=FE=a,AF=AB=6,∠AFE=∠B=90°,进而可得出FC=4,在Rt△CEF中,利用勾股定理可得出关于a的一元二次方程,解之即可得出a值,将其代入8﹣a中即可得出线段CE的长度.
解:在Rt△ABC中,AB=6,BC=8,
∴AC=10.
设BE=a,则CE=8﹣a,
根据翻折的性质可知,BE=FE=a,AF=AB=6,∠AFE=∠B=90°,
∴FC=4.
在Rt△CEF中,EF=a,CE=8﹣a,CF=4,
∴CE2=EF2+CF2,即(8﹣a)2=a2+42,
解得:a=3,
∴8﹣a=5.
故选C.
【点拨】本题考查了翻折变换、矩形的性质、勾股定理以及解一元二次方程,在Rt△CEF中,利用勾股定理找出关于a的一元二次方程是解题的关键.
6.D
【分析】利用菱形的面积等于两对角线之积的一半,求解菱形的面积,再利用等面积法求菱形的高即可.
解:记AC与BD的交点为,
菱形,
菱形的面积
菱形的面积
故选D.
【点拨】本题考查的是菱形的性质,菱形的面积公式,勾股定理.理解菱形的对角线互相垂直平分和学会用等面积法是解题关键.
7.A
【分析】根据正方形的性质,易知∠CAE=∠ACB=45°;等腰△CAE中,根据三角形内角和定理可求得∠ACE的度数,进而可由∠BCE=∠ACE﹣∠ACB得出∠BCE的度数.
解:∵四边形ABCD是正方形,
∴∠CAB=∠BCA=45°;
△ACE中,AC=AE,
则:∠ACE=∠AEC=(180°﹣∠CAE)=67.5°;
∴∠BCE=∠ACE﹣∠ACB=22.5°.
考点:正方形的性质.
8.A
【分析】四边形ABCD的对角线互相平分,则说明四边形是平行四边形,由矩形的判定定理知,只需添加条件是对角线相等或有一内角为直角即可.
解:∵对角线AC与BD互相平分,
∴四边形ABCD是平行四边形,
∴要使四边形ABCD成为矩形,
需添加一个条件是:对角线相等(AC=BD)或有一个内角等于90°.
故选:A.
【点拨】本题考查了平行四边形的判定定理与矩形的判定定理.掌握对角线相等的平行四边形是矩形;有一个角是直角的平行四边形是矩形是解答本题的关键.
9.A
解:因为经过三点可构造三个平行四边形,即 AOBC1、 ABOC2、 AOC3B.根据平行四边形的性质,可知B、C、D正好是C1、C2、C3的坐标,
故选A.
10.D
【分析】确定有关平行四边形,关键是确定平行四边形的四个顶点,由此即可解决问题.
只有②③两块角的两边互相平行,且中间部分相联,角的两边的延长线的交点就是平行四边形的顶点,
∴带②③两块碎玻璃,就可以确定平行四边形的大小.
故选D.
【点拨】本题考查平行四边形的定义以及性质,解题的关键是理解如何确定平行四边形的四个顶点,四个顶点的位置确定了,平行四边形的大小就确定了,属于中考常考题型.
11.A
∵将△ABC沿BC方向平移得到△DCE,
∴ABCD,
∴四边形ABCD为平行四边形,
∴当AB=BC时,平行四边形ABCD是菱形,
故选A.
12.B
试题分析:根据菱形的性质,首先得到AB=AD和BO=DO,再根据等腰三角形的“三线合一”证明⊥BD,故答案选B.
考点:菱形的性质,等腰三角形的性质.
13.5
试题分析:根据直角三角形斜边上的中线等于斜边的一半,可得CE=AB=5.
考点:直角三角形斜边上的中线.
14.20
【分析】根据四边形ABCD为平行四边形可得AE∥BC,根据平行线的性质和角平分线的性质可得出∠ABE=∠AEB,继而可得AB=AE,然后根据已知可求得结果.
解:∵四边形ABCD为平行四边形,
∴AE∥BC,AD=BC,
∴∠AEB=∠EBC,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠ABE=∠AEB,
∴AB=AE,
∴AE+DE=AD=BC=6,
∴AE+2=6,
∴AE=4,
∴AB=CD=4,
∴ ABCD的周长=4+4+6+6=20,
故答案为20.
考点:平行四边形的性质.
15.36°
解:∵四边形ABCD是平行四边形,
∴∠D=∠B=52°,
由折叠的性质得:∠D′=∠D=52°,∠EAD′=∠DAE=20°,
∴∠AEF=∠D+∠DAE=52°+20°=72°,∠AED′=180°-∠EAD′-∠D′=108°,
∴∠FED′=108°-72°=36°;
故答案为36°.
【点拨】本题考查了平行四边形的性质、折叠的性质、三角形的外角性质以及三角形内角和定理;熟练掌握平行四边形的性质和折叠的性质,求出∠AEF和∠AED′是解决问题的关键.
16.5.
试题分析:当B在x轴上时,对角线OB长的最小,如图所示:直线x=1与x轴交于点D,直线x=4与x轴交于点E,根据题意得:∠ADO=∠CEB=90°,OD=1,OE=4,∵四边形ABCD是平行四边形,∴OA∥BC,OA=BC,∴∠AOD=∠CBE,在△AOD和△CBE中,∵∠AOD=∠CBE,∠ADO=∠CEB,OA=BC,∴△AOD≌△CBE(AAS),∴OD=BE=1,∴OB=OE+BE=5;故答案为5.
考点:平行四边形的性质;坐标与图形性质.
17.4.
【分析】连接和,根据全等三角形的判定与性质及中位数定理即可求解.
连接和,因为,,,所以,所以,,所以,又因为是中点,所以是△的中位线,所以,所以.
【点拨】此题主要考查平行四边形的性质,解题的关键是熟知全等三角形的判定与性质及中位线的应用.
18.1
试题分析:根据三角形的中位线定理得:A2B2、B2C2、C2A2分别等于A1B1、B1C1、C1A1的一半,所以△A2B2C2的周长等于△A1B1C1的周长的一半,以此类推可求出△A5B5C5的周长为△A1B1C1的周长的,则周长=(7+4+5)×=1.
考点:三角形中位线的性质.
19.(1)详见解析;(2).
试题分析:(1)由平行四边形的性质和角平分线易证∠BAE=∠BEA,根据等腰三角形的性质可得AB=BE;(2)易证△ABE是等边三角形,根据等边三角形的性质可得AE=AB=4,AF=EF=2,由勾股定理求出BF,再由AAS证明△ADF≌△ECF,即△ADF的面积=△ECF的面积,因此平行四边形ABCD的面积=△ABE的面积=AE BF,即可得出结果.
试题解析:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AB=CD,
∴∠B+∠C=180°,∠AEB=∠DAE,
∵AE是∠BAD的平分线,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴AB=BE,∴BE=CD;
(2)解:∵AB=BE,∠BEA=60°,
∴△ABE是等边三角形,
∴AE=AB=4,
∵BF⊥AE,
∴AF=EF=2,
∴BF=,
∵AD∥BC,
∴∠D=∠ECF,∠DAF=∠E,
在△ADF和△ECF中,
,
∴△ADF≌△ECF(AAS),
∴△ADF的面积=△ECF的面积,
∴平行四边形ABCD的面积=△ABE的面积=AE BF=×4×2=4.
考点:全等三角形的判定与性质;平行四边形的性质.
20.(1)详见解析;(2)3
【分析】(1)由平行四边形的性质和AAS证明△OBE≌△ODF,得出对应边相等即可;
(2)证出AE=GE,再证明DG=DO,得出OF=FG=1,即可得出结果.
解:(1)证明:∵四边形是平行四边形
∴
∴
在与中,
∵
∴
∴
(2)∵
∴
∵
∴
∴
∵
∴
∴
∴
∴
由(1)可知,
∴
∴.
【点拨】本题考查了平行四边形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质;熟练掌握平行四边形的性质,证明三角形全等是解决问题(1)的关键.
21.(1)见解析;(2)96
【分析】(1)根据菱形的性质结合已知条件即可得证;
(2)由(1)所得结合菱形的性质计算出、的长度,再计算面积即可.
解:(1)证明:∵,,
∴四边形AEBO为平行四边形,
又∵四边形ABCD为菱形,
∴,
∴,
∴平行四边形AEBO为矩形;
(2)∵四边形AEBO为矩形,
∴AB=OE=10,
又∵四边形ABCD为菱形,
∴AO=AC=8,
∴,
∴,
∴BD=2BO=12,
∴菱形ABCD的面积=.
【点拨】本题考查了矩形的判定,菱形的性质,勾股定理;掌握好相关的基础知识是解决本题的关键.
22.(1)证明见解析;(2)AB=BC
【分析】(1)由平行四边形的性质可知:OA=OC,OB=OD,再证明OM=ON即可证明四边形AMCN是平行四边形;
(2)当AB=BC时,四边形AMCN是正方形;根据四边形ABCD是平行四边形,AB=BC即可得出四边形ABCD是菱形,再由(1)可知四边形AMCN是矩形;从而得出结论;
(1)证明:四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵对角线BD上的两点M、N满足BM=DN,
∴OB-BM=OD-DN,即OM=ON,
∴四边形AMCN是平行四边形,
∴MN=2OM,
∵ AC=2OM,
∴MN=AC,
∴四边形AMCN是矩形;
(2)当AB=BC时,四边形AMCN是正方形;
∵AB=BC,四边形ABCD是平行四边形,
∴ 四边形ABCD是菱形,
∴ AC⊥BD,
∴AC⊥MN,
由(1)可知四边形ABCD是矩形,
∴四边形ABCD是正方形;
【点拨】本题考查了矩形的判定,平行四边形的判定与性质,正方形的判定,解题的关键是灵活运用所学知识解决问题;
23.(1)证明见解析;(2)四边形EFGH是平行四边形,理由见解析;(3)四边形EFGH的周长一半大于或者等于矩形ABCD一条对角线长度,理由见解析.
【分析】(1)根据全等三角形的判定定理SAS证得结论;
(2)由(1)中全等三角形的性质得到:EH=GF,同理可得FE=HG,即可得四边形EFGH是平行四边形;
(3)由 轴对称--最短路径问题得到:四边形EFGH的周长一半大于或等于矩形ABCD一条对角线长度.
解:(1)∵四边形ABCD是矩形,
∴.
∴在与中,,
∴;
(2)∵由(1)知,,则,同理证得,则,
∴四边形EFGH是平行四边形;
(3) 四边形EFGH的周长一半大于或等于矩形ABCD一条对角线长度.
理由如下:作G关于BC的对称点G′,连接EG′,可得EG′的长度就是EF+FG的最小值.
连接AC,
∵CG′=CG=AE,AB∥CG′,
∴四边形AEG′C为平行四边形,
∴EG′=AC.
在△EFG′中,∵EF+FG′≥EG′=AC,
∴四边形EFGH的周长一半大于或等于矩形ABCD一条对角线长度.
【点拨】考查了矩形的性质,全等三角形的判定与性质.灵活运用这些性质进行推理证明是本题的关键.
24.【探究】FG=FD;【应用】.
试题分析:【探究】连接AF,根据图形猜想FD=FG,由折叠的性质可得AB=AG=AD,再结合AF为△AGF和△ADF的公共边,从而证明△AGF≌△ADF,从而得出结论.
【应用】设FG=x,则FC=5-x,FE=3+x,在RT△ECF中利用勾股定理可求出x的值,进而可得出答案.
【探究】猜想FD=FG.
连接AF,
由折叠的性质可得AB=AG=AD,
在Rt△AGF和Rt△ADF中,
,
∴△AGF≌△ADF.
∴FG=FD;
【应用】设GF=,则CF=5-,则EF=+3
在△ECF中由勾股定理得,,解得
∴FG的长为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
