2021-2022学年北师大版八年级数学下册第一章三角形的证明章节总复习练习A(Word版,附答案)
文档属性
| 名称 | 2021-2022学年北师大版八年级数学下册第一章三角形的证明章节总复习练习A(Word版,附答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 562.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-19 00:00:00 | ||
图片预览



文档简介
北师大数学八年级下册第一章 三角形的证明 章节总复习A(含答案)
姓名:___________班级:___________
一、单选题
1.下列叙述有误的是( )
A.三角形任何两边的和大于第三边
B.对称轴一定垂直平分连结两个对称点的线段
C.所有的等边三角形都是全等图形
D.物体在平面上的位置可以用第几行第几列来确定,也可以用方向和距离来确定
2.下列不能判定△ABC是直角三角形的是( )
A.a2+b2-c2=0 B.a∶b∶c=3∶4∶5
C.∠A∶∠B∶∠C=3:4∶5 D.∠A+∠B=∠C
3.△ABC中,AB=AC,∠A=36°,若按如图的尺规作图方法作出线段BD,则下列结论错误的是( )
A.AD=BD B.∠BDC=72°
C.S△ABD:S△BCD=BC:AC D.△BCD的周长=AB+BC
4.如图,点F在BC上,BC=EF,AB=AE,∠B=∠E,则下列角中,和2∠C度数相等的角是( )
A. B. C. D.
5.等腰三角形的周长为21cm,其中一边长为5cm,则该等腰三角形的底边长为( )
A.5cm B.11cm C.8cm或5cm D.11cm或5cm
6.下列说法中,正确的是( )
A.在轴对称图形中,对应点所连的线段被对称轴垂直平分
B.角的对称轴是角的平分线
C.等腰三角形的高、角平分线、中线重合
D.到三角形三边距离相等的点是三边中垂线的交点
7.如图,直线,且这两条直线之间的距离为8,与的角平分线交于点P,则点P到EF的距离为( )
A.3 B.3.5 C.4 D.4.5
8.如图,在△ABC中,∠1是它的一个外角,E为边AC上一点,延长BC到D,连接DE.则下列结论正确的是( )
A.∠1>∠D B.∠D>∠2 C.∠1=∠2+∠3 D.∠3=∠A
9.如图,在△ABC中,∠C=90°,∠B=15°,AB的垂直平分线交BC于D,交AB于E,若DB=10cm,则CD的长为( )
A.5 B. C. D.10
10.如图,在中,,若以点A为圆心,AC长为半径画弧,交腰BC于点D,则下列结论一定正确的是( )
A. B. C. D.
11.如图:在中,,,,则的度数( )
A.22.5° B.25° C.30° D.45°
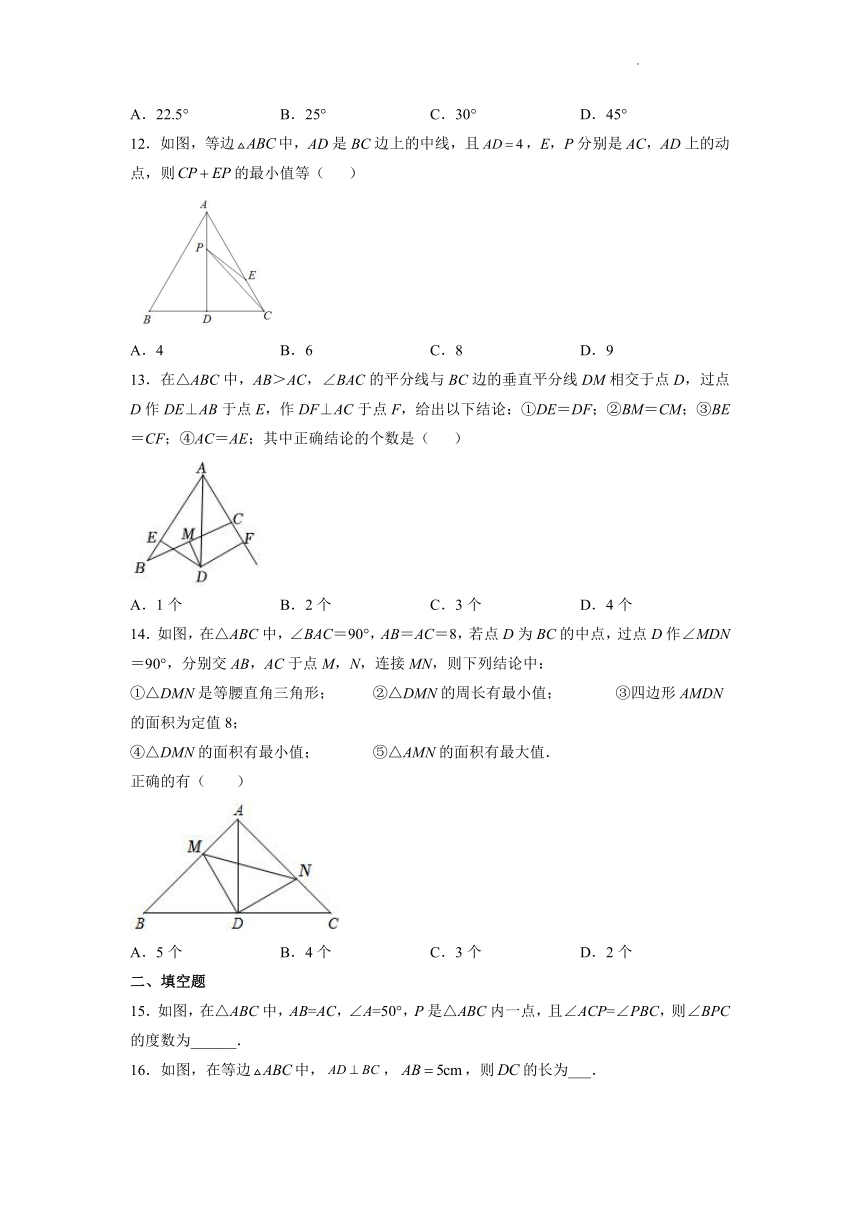
12.如图,等边中,AD是BC边上的中线,且,E,P分别是AC,AD上的动点,则的最小值等( )
A.4 B.6 C.8 D.9
13.在△ABC中,AB>AC,∠BAC的平分线与BC边的垂直平分线DM相交于点D,过点D作DE⊥AB于点E,作DF⊥AC于点F,给出以下结论:①DE=DF;②BM=CM;③BE=CF;④AC=AE;其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
14.如图,在△ABC中,∠BAC=90°,AB=AC=8,若点D为BC的中点,过点D作∠MDN=90°,分别交AB,AC于点M,N,连接MN,则下列结论中:
①△DMN是等腰直角三角形; ②△DMN的周长有最小值; ③四边形AMDN的面积为定值8;
④△DMN的面积有最小值; ⑤△AMN的面积有最大值.
正确的有( )
A.5个 B.4个 C.3个 D.2个
二、填空题
15.如图,在△ABC中,AB=AC,∠A=50°,P是△ABC内一点,且∠ACP=∠PBC,则∠BPC的度数为______.
16.如图,在等边中,,,则的长为___.
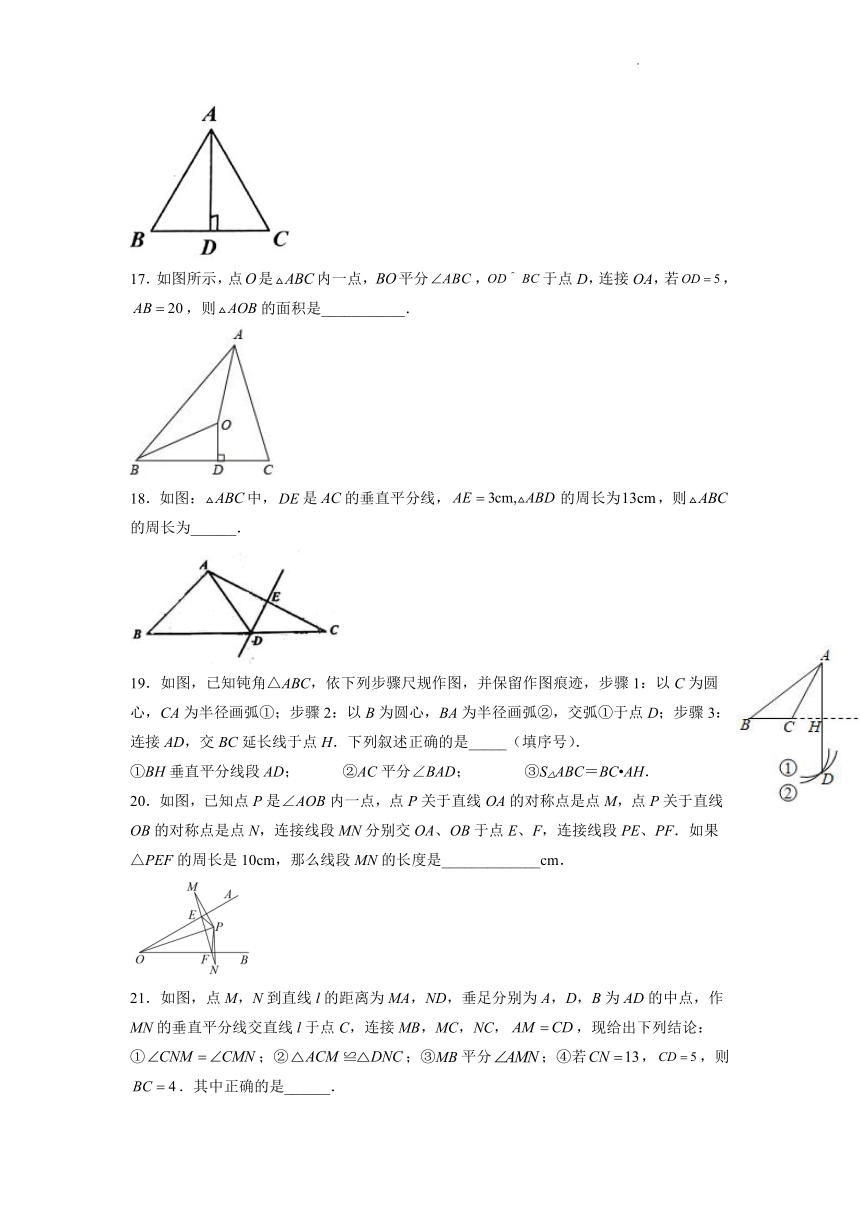
17.如图所示,点是内一点,平分,于点D,连接OA,若,,则的面积是___________.
18.如图:中,是的垂直平分线,的周长为,则的周长为______.
19.如图,已知钝角△ABC,依下列步骤尺规作图,并保留作图痕迹,步骤1:以C为圆心,CA为半径画弧①;步骤2:以B为圆心,BA为半径画弧②,交弧①于点D;步骤3:连接AD,交BC延长线于点H.下列叙述正确的是_____(填序号).
①BH垂直平分线段AD; ②AC平分∠BAD; ③S△ABC=BC AH.
20.如图,已知点P是∠AOB内一点,点P关于直线OA的对称点是点M,点P关于直线OB的对称点是点N,连接线段MN分别交OA、OB于点E、F,连接线段PE、PF.如果△PEF的周长是10cm,那么线段MN的长度是_____________cm.
21.如图,点M,N到直线l的距离为MA,ND,垂足分别为A,D,B为AD的中点,作MN的垂直平分线交直线l于点C,连接MB,MC,NC,,现给出下列结论:①;②;③MB平分;④若,,则.其中正确的是______.
22.如图,在ABC中,AB=AC=10,AD=8,AD、BE分别是ABC边BC、AC上的高,P是AD上的动点,则CPE周长的最小值是______.
三、解答题
23.如图,已知().请用无刻度的直尺和圆规,完成下列作图(不要求写作法,保留作图痕迹):
(1)在边上找一点,使得直线平分的面积,请在图(1)中作图;
(2)在边上找一点,使得点到边的距离等于线段的长,请在图(2)中作图.
24.已知:如图,在四边形ABCD中,AB∥CD,且AB=CD,点E在AB上,将△BCE沿CE对折得到△FCE,EF恰好过点A,FC边与AD边交于点G,且DC=DG.
(1)求证:△ABC≌△CDA;
(2)试判断△FAG的形状,并说明理由.
25.在△ABC中,AC=BC,∠ACB=90°,直线MN经过点C,过A、B两点分别作AD⊥MN于点D,BE⊥MN于点E.
(1)如图1,试说明BE、AD、DE三线段之间的等量关系,并说明理由;
(2)若MN绕点C旋转到(图2)时,(1)中的关系还成立吗?若成立说明理由,若不成立请写出他们之间的等量关系并说明理由.
(3)若MN绕点C旋转到(图3)时,请直接写出BE、AD、DE三者之间的等量关系(不需证明).
26.已已知a、b、c为△ABC的三边长,且b、c满足(b-5)2+(c-7)2=0,a为方程|a-3|=2的解,求△ABC的周长,并判断△ABC的形状.
27.在△ABC中,AC=BC,∠ACB=90°,点D、E分别在AB、BC上,且AD=BE,BD=AC,连接CD、DE.
(1)如图1,求证:DE=CD;
(2)如图2,过E作EF⊥AB于F,求证:∠FED=∠CED;
(3)如图3,若延长ED、CA相交于G,求证:D为EG的中点.
28.如图1,在△ABC中,,点E在线段BC上,连接AE并延长到G,使得,过点G作分别交BC,AC于点F,D.
(1)求证:;
(2)若,,求AB的长度;
(3)如图2,过点D作于H,P是直线DH上的一个动点,连接AF,AP,FP,若,,在(2)条件下,求△AFP周长的最小值.
29.已知:如图,在等边△ABC中,点O是BC的中点,∠DOE=120°,∠DOE绕着点O旋转,角的两边与AB相交于点D,与AC相交于点E.
(1)若OD,OE都在BC的上方,如图1,求证:OD=OE.
(2)在图1中,BD,CE与BC的数量关系是 .
(3)若点D在AB的延长线上,点E在线段AC上,如图2,直接写出BD,CE与BC的数量关系是 .
30.在等边三角形的两边、所在直线上分别有两点、,为外一点,且,,.探究;当点、分别在直线、上移动时,,,之间的数量关系.
(1)如图①,当点、在边、上,且时,试说明.
(2)如图②,当点、在边、上,且时,还成立吗?
答:________(请在空格内填“一定成立”“不一定成立”或“一定不成立”).
(3)如图③,当点、分别在边、的延长线上时,请直接写出,,之间的数量关系.
参考答案:
1.C 2.C 3.C 4.D 5.A 6.A 7.C 8.A 9.B 10.B 11.A 12.A
13.C 14.B
15.115°
16.
17.50
18.19cm
19.①
20.10
21.①②
22.16.8
23.(1)解:如图所示,
(2)解:如图所示,
24.(1)证明:∵AB∥CD,
∴∠BAC=∠DCA,
∵在△BCA和△DCA中,
,
∴△BAC≌△DCA(SAS);
(2)解:△FAG是等边三角形.理由如下:
∵△BAC≌△DCA,
∴∠BCA=∠DAC,
∴BC∥AD,
∴∠FAG=∠ABC,
由折叠的性质知:∠ABC =∠BFC,
∴∠FAG=∠AFG,
∵DC=DG,
∴∠DCG=∠DGC=∠FGA,
∵AB∥CD,
∴∠AFG=∠DCG,
∴∠FAG=∠AFG=∠FGA,
所以△FAG是等边三角形.
25.(1)∵∠ACB=90°,AD⊥MN,BE⊥MN,
∴∠ACD+∠BCE=90°,∠CBE+∠BCE=90°,
∴∠ACD=∠CBE,
∵AC=BC,
∴△ADC≌△CEB,
∴AD=CE,DC=BE,
∵DE=DC+CE,
∴DE=AD+BE.
(2)不成立,结论是BE=DE+AD,理由如下:
∵∠ACB=90°,AD⊥MN,BE⊥MN,
∴∠ACD+∠BCE=90°,∠CBE+∠BCE=90°,
∴∠ACD=∠CBE,
∵AC=BC,
∴△ADC≌△CEB,
∴AD=CE,DC=BE,
∵DC=DE+CE,
∴BE=AD+DE.
(3)BE、AD、DE三者之间的等量关系是AD=DE+BE.
∵∠ACB=90°,AD⊥MN,BE⊥MN,
∴∠ACD+∠BCE=90°,∠CBE+∠BCE=90°,
∴∠ACD=∠CBE,
∵AC=BC,
∴△ADC≌△CEB,
∴AD=CE,DC=BE,
∵CE=DC+DE,
∴AD=DE+BE.
26.解:∵(b-5)2+(c-7)2=0,
∴,
解得,
∵a为方程|a-3|=2的解,
∴a=5或1,
当a=1,b=5,c=7时,1+5<7,
不能组成三角形,故a=1不合题意;
∴a=5,
∴△ABC的周长=5+5+7=17,
∵a=b=5,
∴△ABC是等腰三角形.
27.(1)证明:∵△ABC为等腰直角三角形,
∴∠A=∠B=45°,
在△ACD和△BDE中,
∵,
∴△ACD≌△BDE(SAS),
∴DC=DE;
(2)证明:∵AC=BC,∠ACB=90°,
∴∠A=∠B=45°,
∵AC=BC,BD=AC,
∴BD=BC,
∴∠BCD=∠BDC==67.5°,
∴∠ACD=∠ACB-∠BCD=90°-67.5°=22.5°,
∵△ACD≌△BDE(SAS),
∴∠ACD=∠BDE=22.5°,
∴∠CED=22.5°+45°=67.5°,
∵EF⊥AB,
∴∠EFD=90°,
∴∠DEF=90°-22.5°=67.5°,
∴∠FED=∠CED;
(3)证明:∵DC=DE,
∴∠DCE=∠DEC,
∵∠ACB=90°,
∴∠G+∠CEG=90°,∠DCE+∠DCG=90°,
∴∠G=∠DCG,
∴DG=DC,
∴DG=DE,即点D是EG的中点.
28.(1)证明:如图1中,∵,∴.
在△ABE和△GFE中,
∴.
(2)解:如图1中,∵,∴.
∵,∴,∴.
∴.
∵,∴.
∵,∴.
(3)解:如图2中,∵,
∴,∴.
∵,∴,即.
∵,,
∴,∴,
∴,
∴,
∴.
∵,
∴,
∴点F与点C关于直线PD对称,
∴当点P与D重合时,△PAF的周长最小,最小值为的周长为:
.
29.(1)证明:取AB的中点F,连接OF.
∵△ABC是等边三角形,
∴,
∵点O与点F分别是BC与AB的中点,
∴,
∴△BOF是等边三角形,
∴,
,
∴,
∴,
∵在△DOF和△EOC中,
,
∴,
∴.
(2)解:结论:.
理由:∵,
∴,
∴,
∵是等边三角形,
∴,
∵,
∴.
故答案为:;
(3)结论:.
理由如图2中,取的中点F,连接OF.
同(1)中的方法可证是等边三角形,,
∴,
∴,
∵,
∴
30.(1)∵PM=PN,∠MPN=60°,
∴△MPN是等边三角形,
∵△ABC是等边三角形,
∴∠A=∠ABC=∠ACB=60°,
∵BP=CP,∠BPC=120°,
∴∠PBC=∠PCB=,
∴∠MBP=∠NCP=60°+30°=90°
∵PM=PN,BP=CP,
∴Rt△BPM≌Rt△CPN(HL),
∴∠BPM=∠CPN=30°,BM=CN,
∴PM=2BM,PN=2CN,
∴MN=2BM=2CN=BM+CN;
(2)延长到,使,连接,
由(1 )知,
,
,
在和中,
,
,
,,
,,
,
在和中,
,
,
,
,
.
故答案为:一定成立.
(3)
在上截取,连接,
在和中,
,
,
,,
,
,
,
,
在和中,
,
,
,
,
.
答案第1页,共2页
姓名:___________班级:___________
一、单选题
1.下列叙述有误的是( )
A.三角形任何两边的和大于第三边
B.对称轴一定垂直平分连结两个对称点的线段
C.所有的等边三角形都是全等图形
D.物体在平面上的位置可以用第几行第几列来确定,也可以用方向和距离来确定
2.下列不能判定△ABC是直角三角形的是( )
A.a2+b2-c2=0 B.a∶b∶c=3∶4∶5
C.∠A∶∠B∶∠C=3:4∶5 D.∠A+∠B=∠C
3.△ABC中,AB=AC,∠A=36°,若按如图的尺规作图方法作出线段BD,则下列结论错误的是( )
A.AD=BD B.∠BDC=72°
C.S△ABD:S△BCD=BC:AC D.△BCD的周长=AB+BC
4.如图,点F在BC上,BC=EF,AB=AE,∠B=∠E,则下列角中,和2∠C度数相等的角是( )
A. B. C. D.
5.等腰三角形的周长为21cm,其中一边长为5cm,则该等腰三角形的底边长为( )
A.5cm B.11cm C.8cm或5cm D.11cm或5cm
6.下列说法中,正确的是( )
A.在轴对称图形中,对应点所连的线段被对称轴垂直平分
B.角的对称轴是角的平分线
C.等腰三角形的高、角平分线、中线重合
D.到三角形三边距离相等的点是三边中垂线的交点
7.如图,直线,且这两条直线之间的距离为8,与的角平分线交于点P,则点P到EF的距离为( )
A.3 B.3.5 C.4 D.4.5
8.如图,在△ABC中,∠1是它的一个外角,E为边AC上一点,延长BC到D,连接DE.则下列结论正确的是( )
A.∠1>∠D B.∠D>∠2 C.∠1=∠2+∠3 D.∠3=∠A
9.如图,在△ABC中,∠C=90°,∠B=15°,AB的垂直平分线交BC于D,交AB于E,若DB=10cm,则CD的长为( )
A.5 B. C. D.10
10.如图,在中,,若以点A为圆心,AC长为半径画弧,交腰BC于点D,则下列结论一定正确的是( )
A. B. C. D.
11.如图:在中,,,,则的度数( )
A.22.5° B.25° C.30° D.45°
12.如图,等边中,AD是BC边上的中线,且,E,P分别是AC,AD上的动点,则的最小值等( )
A.4 B.6 C.8 D.9
13.在△ABC中,AB>AC,∠BAC的平分线与BC边的垂直平分线DM相交于点D,过点D作DE⊥AB于点E,作DF⊥AC于点F,给出以下结论:①DE=DF;②BM=CM;③BE=CF;④AC=AE;其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
14.如图,在△ABC中,∠BAC=90°,AB=AC=8,若点D为BC的中点,过点D作∠MDN=90°,分别交AB,AC于点M,N,连接MN,则下列结论中:
①△DMN是等腰直角三角形; ②△DMN的周长有最小值; ③四边形AMDN的面积为定值8;
④△DMN的面积有最小值; ⑤△AMN的面积有最大值.
正确的有( )
A.5个 B.4个 C.3个 D.2个
二、填空题
15.如图,在△ABC中,AB=AC,∠A=50°,P是△ABC内一点,且∠ACP=∠PBC,则∠BPC的度数为______.
16.如图,在等边中,,,则的长为___.
17.如图所示,点是内一点,平分,于点D,连接OA,若,,则的面积是___________.
18.如图:中,是的垂直平分线,的周长为,则的周长为______.
19.如图,已知钝角△ABC,依下列步骤尺规作图,并保留作图痕迹,步骤1:以C为圆心,CA为半径画弧①;步骤2:以B为圆心,BA为半径画弧②,交弧①于点D;步骤3:连接AD,交BC延长线于点H.下列叙述正确的是_____(填序号).
①BH垂直平分线段AD; ②AC平分∠BAD; ③S△ABC=BC AH.
20.如图,已知点P是∠AOB内一点,点P关于直线OA的对称点是点M,点P关于直线OB的对称点是点N,连接线段MN分别交OA、OB于点E、F,连接线段PE、PF.如果△PEF的周长是10cm,那么线段MN的长度是_____________cm.
21.如图,点M,N到直线l的距离为MA,ND,垂足分别为A,D,B为AD的中点,作MN的垂直平分线交直线l于点C,连接MB,MC,NC,,现给出下列结论:①;②;③MB平分;④若,,则.其中正确的是______.
22.如图,在ABC中,AB=AC=10,AD=8,AD、BE分别是ABC边BC、AC上的高,P是AD上的动点,则CPE周长的最小值是______.
三、解答题
23.如图,已知().请用无刻度的直尺和圆规,完成下列作图(不要求写作法,保留作图痕迹):
(1)在边上找一点,使得直线平分的面积,请在图(1)中作图;
(2)在边上找一点,使得点到边的距离等于线段的长,请在图(2)中作图.
24.已知:如图,在四边形ABCD中,AB∥CD,且AB=CD,点E在AB上,将△BCE沿CE对折得到△FCE,EF恰好过点A,FC边与AD边交于点G,且DC=DG.
(1)求证:△ABC≌△CDA;
(2)试判断△FAG的形状,并说明理由.
25.在△ABC中,AC=BC,∠ACB=90°,直线MN经过点C,过A、B两点分别作AD⊥MN于点D,BE⊥MN于点E.
(1)如图1,试说明BE、AD、DE三线段之间的等量关系,并说明理由;
(2)若MN绕点C旋转到(图2)时,(1)中的关系还成立吗?若成立说明理由,若不成立请写出他们之间的等量关系并说明理由.
(3)若MN绕点C旋转到(图3)时,请直接写出BE、AD、DE三者之间的等量关系(不需证明).
26.已已知a、b、c为△ABC的三边长,且b、c满足(b-5)2+(c-7)2=0,a为方程|a-3|=2的解,求△ABC的周长,并判断△ABC的形状.
27.在△ABC中,AC=BC,∠ACB=90°,点D、E分别在AB、BC上,且AD=BE,BD=AC,连接CD、DE.
(1)如图1,求证:DE=CD;
(2)如图2,过E作EF⊥AB于F,求证:∠FED=∠CED;
(3)如图3,若延长ED、CA相交于G,求证:D为EG的中点.
28.如图1,在△ABC中,,点E在线段BC上,连接AE并延长到G,使得,过点G作分别交BC,AC于点F,D.
(1)求证:;
(2)若,,求AB的长度;
(3)如图2,过点D作于H,P是直线DH上的一个动点,连接AF,AP,FP,若,,在(2)条件下,求△AFP周长的最小值.
29.已知:如图,在等边△ABC中,点O是BC的中点,∠DOE=120°,∠DOE绕着点O旋转,角的两边与AB相交于点D,与AC相交于点E.
(1)若OD,OE都在BC的上方,如图1,求证:OD=OE.
(2)在图1中,BD,CE与BC的数量关系是 .
(3)若点D在AB的延长线上,点E在线段AC上,如图2,直接写出BD,CE与BC的数量关系是 .
30.在等边三角形的两边、所在直线上分别有两点、,为外一点,且,,.探究;当点、分别在直线、上移动时,,,之间的数量关系.
(1)如图①,当点、在边、上,且时,试说明.
(2)如图②,当点、在边、上,且时,还成立吗?
答:________(请在空格内填“一定成立”“不一定成立”或“一定不成立”).
(3)如图③,当点、分别在边、的延长线上时,请直接写出,,之间的数量关系.
参考答案:
1.C 2.C 3.C 4.D 5.A 6.A 7.C 8.A 9.B 10.B 11.A 12.A
13.C 14.B
15.115°
16.
17.50
18.19cm
19.①
20.10
21.①②
22.16.8
23.(1)解:如图所示,
(2)解:如图所示,
24.(1)证明:∵AB∥CD,
∴∠BAC=∠DCA,
∵在△BCA和△DCA中,
,
∴△BAC≌△DCA(SAS);
(2)解:△FAG是等边三角形.理由如下:
∵△BAC≌△DCA,
∴∠BCA=∠DAC,
∴BC∥AD,
∴∠FAG=∠ABC,
由折叠的性质知:∠ABC =∠BFC,
∴∠FAG=∠AFG,
∵DC=DG,
∴∠DCG=∠DGC=∠FGA,
∵AB∥CD,
∴∠AFG=∠DCG,
∴∠FAG=∠AFG=∠FGA,
所以△FAG是等边三角形.
25.(1)∵∠ACB=90°,AD⊥MN,BE⊥MN,
∴∠ACD+∠BCE=90°,∠CBE+∠BCE=90°,
∴∠ACD=∠CBE,
∵AC=BC,
∴△ADC≌△CEB,
∴AD=CE,DC=BE,
∵DE=DC+CE,
∴DE=AD+BE.
(2)不成立,结论是BE=DE+AD,理由如下:
∵∠ACB=90°,AD⊥MN,BE⊥MN,
∴∠ACD+∠BCE=90°,∠CBE+∠BCE=90°,
∴∠ACD=∠CBE,
∵AC=BC,
∴△ADC≌△CEB,
∴AD=CE,DC=BE,
∵DC=DE+CE,
∴BE=AD+DE.
(3)BE、AD、DE三者之间的等量关系是AD=DE+BE.
∵∠ACB=90°,AD⊥MN,BE⊥MN,
∴∠ACD+∠BCE=90°,∠CBE+∠BCE=90°,
∴∠ACD=∠CBE,
∵AC=BC,
∴△ADC≌△CEB,
∴AD=CE,DC=BE,
∵CE=DC+DE,
∴AD=DE+BE.
26.解:∵(b-5)2+(c-7)2=0,
∴,
解得,
∵a为方程|a-3|=2的解,
∴a=5或1,
当a=1,b=5,c=7时,1+5<7,
不能组成三角形,故a=1不合题意;
∴a=5,
∴△ABC的周长=5+5+7=17,
∵a=b=5,
∴△ABC是等腰三角形.
27.(1)证明:∵△ABC为等腰直角三角形,
∴∠A=∠B=45°,
在△ACD和△BDE中,
∵,
∴△ACD≌△BDE(SAS),
∴DC=DE;
(2)证明:∵AC=BC,∠ACB=90°,
∴∠A=∠B=45°,
∵AC=BC,BD=AC,
∴BD=BC,
∴∠BCD=∠BDC==67.5°,
∴∠ACD=∠ACB-∠BCD=90°-67.5°=22.5°,
∵△ACD≌△BDE(SAS),
∴∠ACD=∠BDE=22.5°,
∴∠CED=22.5°+45°=67.5°,
∵EF⊥AB,
∴∠EFD=90°,
∴∠DEF=90°-22.5°=67.5°,
∴∠FED=∠CED;
(3)证明:∵DC=DE,
∴∠DCE=∠DEC,
∵∠ACB=90°,
∴∠G+∠CEG=90°,∠DCE+∠DCG=90°,
∴∠G=∠DCG,
∴DG=DC,
∴DG=DE,即点D是EG的中点.
28.(1)证明:如图1中,∵,∴.
在△ABE和△GFE中,
∴.
(2)解:如图1中,∵,∴.
∵,∴,∴.
∴.
∵,∴.
∵,∴.
(3)解:如图2中,∵,
∴,∴.
∵,∴,即.
∵,,
∴,∴,
∴,
∴,
∴.
∵,
∴,
∴点F与点C关于直线PD对称,
∴当点P与D重合时,△PAF的周长最小,最小值为的周长为:
.
29.(1)证明:取AB的中点F,连接OF.
∵△ABC是等边三角形,
∴,
∵点O与点F分别是BC与AB的中点,
∴,
∴△BOF是等边三角形,
∴,
,
∴,
∴,
∵在△DOF和△EOC中,
,
∴,
∴.
(2)解:结论:.
理由:∵,
∴,
∴,
∵是等边三角形,
∴,
∵,
∴.
故答案为:;
(3)结论:.
理由如图2中,取的中点F,连接OF.
同(1)中的方法可证是等边三角形,,
∴,
∴,
∵,
∴
30.(1)∵PM=PN,∠MPN=60°,
∴△MPN是等边三角形,
∵△ABC是等边三角形,
∴∠A=∠ABC=∠ACB=60°,
∵BP=CP,∠BPC=120°,
∴∠PBC=∠PCB=,
∴∠MBP=∠NCP=60°+30°=90°
∵PM=PN,BP=CP,
∴Rt△BPM≌Rt△CPN(HL),
∴∠BPM=∠CPN=30°,BM=CN,
∴PM=2BM,PN=2CN,
∴MN=2BM=2CN=BM+CN;
(2)延长到,使,连接,
由(1 )知,
,
,
在和中,
,
,
,,
,,
,
在和中,
,
,
,
,
.
故答案为:一定成立.
(3)
在上截取,连接,
在和中,
,
,
,,
,
,
,
,
在和中,
,
,
,
,
.
答案第1页,共2页
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
