2021-2022学年苏科版八年级数学下册第9章中心对称图形—平行四边形单元整合练习题(基础)(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版八年级数学下册第9章中心对称图形—平行四边形单元整合练习题(基础)(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 843.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-19 21:08:49 | ||
图片预览

文档简介
第9章 中心对称图形—平行四边形 单元整合练习题(基础)
2021-2022学年苏科版八年级数学下册
一、选择题
1、(2020秋 盘龙区期末)我国民间,流传着许多含有吉祥意义的文字图案,表示对幸福生活的向往,良辰佳节的祝贺.比如下列图案分别表示“福”、“禄”、“寿”、“喜”,其中是中心对称图形的是( )
A.①③ B.①④ C.②③ D.②④
2、(2021·广东广州市·八年级期末)如图,在四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )
A.AB∥CD,AD∥BC B.AD∥BC,AB=CD
C.OA=OC,OB=OD D.AB=CD,AD=BC
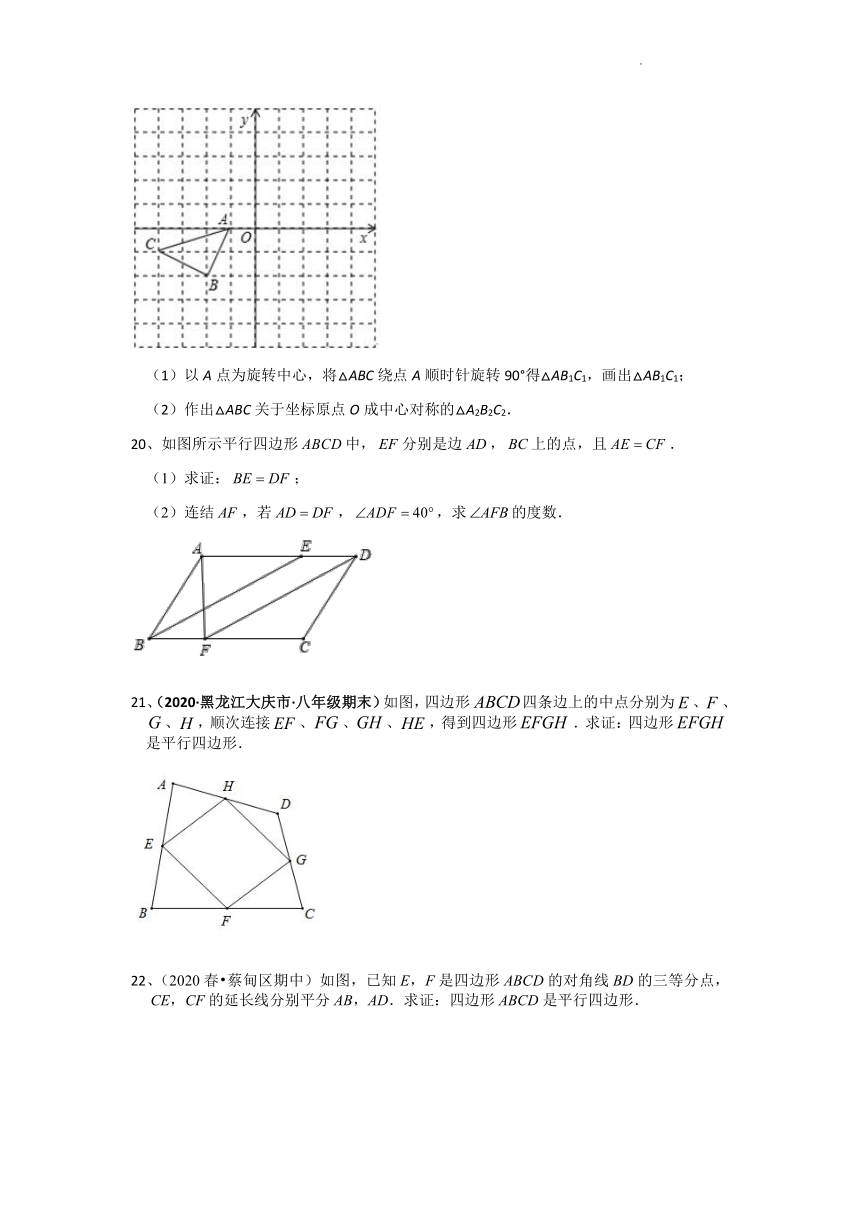
3、(2020秋 朝阳区校级月考)如图,在 ABCD中,已知AC=4cm,若△ACD的周长为14cm,则 ABCD的周长为( )
A.14cm B.28cm C.10cm D.20cm
4、如图,在菱形ABCD中,对角线AC,BD相交于点O,AC=8,BD=6,点E,F分别为AO,DO的中点,则线段EF的长为( )
A.2.5 B.3 C.4 D.5
5、如图,在中,,将绕点按逆时针方向旋转得到△.若点恰好落在边上,且,则的度数为
A. B. C. D.
6、如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=2,则矩形的对角线AC的长是( )
A.2 B.4 C.2 D.4
7、如图,下列条件不能判定四边形ABCD是矩形的是( )
A.∠DAB=∠ABC=∠BCD=90° B.AB∥CD,AB=CD,AB⊥AD
C.AO=BO,CO=DO D.AO=BO=CO=DO
8、如图,四边形ABCD的对角线互相平分,要使它变为菱形,需要添加的条件是( )
A.AB=CD B.AD=BC C.AC=BD D.AB=BC
9、(2020春 温州期中)如图,菱形ABCD的对角线相交于点O,AC=12,BD=16,点P为边BC上一点,且P不与B、C重合.过P作PE⊥AC于E,PF⊥BD于F,连结EF,则EF的最小值为( )
A.4 B.4.8 C.5 D.6
10、如图,点M是正方形ABCD边CD上一点,连接AM,作DE⊥AM于点F,连接BE.若AF=1,四边形ABED的面积为6,则BF的长为( )
A.2 B.3 C. D.
二、填空题
11、(2021·山东泰安市·九年级期末)如图:在中,点分别是的中点,连接,如果那么的周长是___.
12、(2019 达州)如图, ABCD的对角线AC、BD相交于点O,点E是AB的中点,△BEO的周长是8,则△BCD的周长为 .
13、如图,矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AC=8,则EF=________.
14、(2021春 崇川区期末)已知菱形中,,连接,则等于
A. B. C. D.
15、(2020春 滨湖区期中)如图,在四边形ABCD中,点E、F分别是线段AD、BC的中点,G、H分别是线段BD、AC的中点,当四边形ABCD的边满足 时,四边形EGFH是菱形.
16、(2020春 常州期中)如图,正方形中,点、分别是、边上的点,且,垂足为点,的面积为,则图中阴影部分的面积为 .
17、(2020春 曲阜市期末)如图,正方形ABCD的边长是2,对角线AC、BD相交于点O,点E、F分别在边AD、AB上,且OE⊥OF,则四边形AFOE的面积为 .
18、如图,在中,,为的中线,过点作于点,过点作的平行线,交的延长线于点,在的延长线上截取,连接、.若,,则 .
三、解答题
19、如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图.
(1)以A点为旋转中心,将△ABC绕点A顺时针旋转90°得△AB1C1,画出△AB1C1;
(2)作出△ABC关于坐标原点O成中心对称的△A2B2C2.
20、如图所示平行四边形中,分别是边,上的点,且.
(1)求证:;
(2)连结,若,,求的度数.
21、(2020·黑龙江大庆市·八年级期末)如图,四边形四条边上的中点分别为、、、,顺次连接、、、,得到四边形.求证:四边形是平行四边形.
22、(2020春 蔡甸区期中)如图,已知E,F是四边形ABCD的对角线BD的三等分点,CE,CF的延长线分别平分AB,AD.求证:四边形ABCD是平行四边形.
23、如图,将的边延长至点,使,连接,,,交于点
(1)求证:;
(2)若,求证:四边形是矩形.
24、(2020春 博白县期末)如图,正方形ABCD边长为8,E,F分别是BC,CD上的点,且AE⊥BF.
(1)求证:AE=BF.
(2)若AF=10,求AE的长.
25、如图,在中,,是上任一点,且.
(1)若平分,求证:;
(2)若,且在中点时,试判断四边形的形状,并说明你的理由.
26、(2020 朝阳区一模)如图,四边形ABCD是平行四边形,AE⊥BC,AF⊥CD,垂足分别为E,F,且BE=DF.
(1)求证:四边形ABCD是菱形;
(2)连接EF并延长,交AD的延长线于点G,若∠CEG=30°,AE=2,求EG的长.
27、(2020 官渡区二模)如图,在平行四边形ABCD中,AC,BD交于点O,且AO=BO,∠ADB的平分线DE交AB于点E.
(1)求证:四边形ABCD是矩形.
(2)若AB=8,OC=5,求AE的长.
第9章 中心对称图形—平行四边形 单元整合练习题(基础)
2021-2022学年苏科版八年级数学下册(解析)
一、选择题
1、(2020秋 盘龙区期末)我国民间,流传着许多含有吉祥意义的文字图案,表示对幸福生活的向往,良辰佳节的祝贺.比如下列图案分别表示“福”、“禄”、“寿”、“喜”,其中是中心对称图形的是( )
A.①③ B.①④ C.②③ D.②④
【点拨】根据中心对称图形的定义,结合选项所给图形进行判断即可.
【解析】解:①不是中心对称图形,故本选项不合题意;
②是中心对称图形,故本选项符合题意;
③不是中心对称图形,故本选项不合题意;
④是中心对称图形,故本选项符合题意;
故选:D.
2、(2021·广东广州市·八年级期末)如图,在四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )
A.AB∥CD,AD∥BC B.AD∥BC,AB=CD
C.OA=OC,OB=OD D.AB=CD,AD=BC
【答案】B
【分析】根据平行四边形的判定方法即可判断.
【详解】A、根据两组对边分别平行的四边形是平行四边形,可以判定;
B、无法判定,四边形可能是等腰梯形,也可能是平行四边形;
C、根据对角线互相平分的四边形是平行四边形,可以判定;
D、根据两组对边分别相等的四边形是平行四边形,可以判定;故选:B.
3、(2020秋 朝阳区校级月考)如图,在 ABCD中,已知AC=4cm,若△ACD的周长为14cm,则 ABCD的周长为( )
A.14cm B.28cm C.10cm D.20cm
【点拨】先根据AC=4cm,△ACD的周长为14cm得出AD+CD=10cm,再结合四边形ABCD是平行四边形知AB=CD、BC=AD,从而得出答案.
【解析】解:∵△ACD的周长为14cm,即AD+CD+AC=14cm,且AC=4cm,
∴AD+CD=10cm,
∵四边形ABCD是平行四边形,
∴AB=CD、BC=AD,
则 ABCD的周长为AB+BC+AD+CD=10+10=20(cm),
故选:D.
4、如图,在菱形ABCD中,对角线AC,BD相交于点O,AC=8,BD=6,点E,F分别为AO,DO的中点,则线段EF的长为( )
A.2.5 B.3 C.4 D.5
【分析】本题考查了菱形的性质、勾股定理、三角形的中位线定理,利用勾股定理求得AD的长是解题的关键.
先依据菱形的性质求得OA、OD的长,然后依据勾股定理可求得AD的长,最后依据三角形中位线定理求的EF的长即可.
【解答】解:∵四边形ABCD为菱形,
∴AC⊥BD,OA=OC=AC=4,OB=OD=BD=3.
在Rt△AOD中,依据勾股定理可知:AD===5.
∵点E,F分别为AO,DO的中点,
∴EF是△AOD的中位线,
∴EF=AD=2.5;
故选:A.
5、如图,在中,,将绕点按逆时针方向旋转得到△.若点恰好落在边上,且,则的度数为
A. B. C. D.
【分析】由旋转的性质可得,,由等腰三角形的性质可得,,由三角形的外角性质和三角形内角和定理可求解.
【解析】,
,
,
将绕点按逆时针方向旋转得到△,
,,
,
,
,
,
,
故选:.
6、如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=2,则矩形的对角线AC的长是( )
A.2 B.4 C.2 D.4
【答案】B
【解析】∵四边形ABCD是矩形,∴OA=OC=OB=OD.∴△OAB是等腰三角形.
∵∠AOB=60° ,∴△OAB是等边三角形,∴AB=OA.
∵AB=2,AB=OA,∴OA=2.
∵OA=OC,OA=2,∴AC=4.
故选B.
7、如图,下列条件不能判定四边形ABCD是矩形的是( )
A.∠DAB=∠ABC=∠BCD=90° B.AB∥CD,AB=CD,AB⊥AD
C.AO=BO,CO=DO D.AO=BO=CO=DO
解;A、∠DAB=∠ABC=∠BCD=90°根据有三个角是直角的四边形是矩形可判定为矩形,故此选项错误;
B、AB∥CD,AB=CD,可以判定为平行四边形,又有AB⊥AD,可判定为矩形,故此选项错误;
C、AO=BO,CO=DO,不可以判定为平行四边形,所以不可判定为矩形,故此选项正确;
D、AO=BO=CO=DO,可以得到对角线互相平分且相等,据此可以判定矩形,故此选项错误.
故选:C.
8、如图,四边形ABCD的对角线互相平分,要使它变为菱形,需要添加的条件是( )
A.AB=CD B.AD=BC C.AC=BD D.AB=BC
【思路点拨】由已知条件得出四边形ABCD是平行四边形,再由一组邻边相等,即可得出四边形ABCD是菱形.
【答案】解:需要添加的条件是AB=BC;
理由如下:
∵四边形ABCD的对角线互相平分,
∴四边形ABCD是平行四边形,
∵AB=BC,
∴平行四边形ABCD是菱形(一组邻边相等的平行四边形是菱形);
故选:D.
9、(2020春 温州期中)如图,菱形ABCD的对角线相交于点O,AC=12,BD=16,点P为边BC上一点,且P不与B、C重合.过P作PE⊥AC于E,PF⊥BD于F,连结EF,则EF的最小值为( )
A.4 B.4.8 C.5 D.6
【思路点拨】由菱形的性质可得AC⊥BD,BO=BD=8,OC=AC=6,由勾股定理可求BC的长,可证四边形OEPF是矩形,可得EF=OP,OP⊥BC时,OP有最小值,由面积法可求解.
【答案】解:连接OP,
∵四边形ABCD是菱形,AC=12,BD=16,
∴AC⊥BD,BO=BD=8,OC=AC=6,∴BC===10,
∵PE⊥AC,PF⊥BD,AC⊥BD,∴四边形OEPF是矩形,∴FE=OP,
∵当OP⊥BC时,OP有最小值,此时S△OBC=OB×OC=BC×OP,
∴OP==4.8,∴EF的最小值为4.8,
故选:B.
10、如图,点M是正方形ABCD边CD上一点,连接AM,作DE⊥AM于点F,连接BE.若AF=1,四边形ABED的面积为6,则BF的长为( )
A.2 B.3 C. D.
【点拨】证明△ABF≌△DAE得BF=AF,AF=DE,进而由已知四边形的面积列出BF的方程进行解答便可.
【解析】解:∵四边形ABCD是正方形,∴AB=AD,∠BAD=90°,
∵BF⊥AM,∴∠ABF+∠BAF=∠BAF+∠DAE=90°,∴∠ABF=∠DAE,
∵DE⊥AM,∴∠AFB=∠DEA=90°,∴△ABF≌△DAE(AAS),
∴BF=AE,AF=DE=1,
设BF=AE=x,则EF=x﹣1,
∵四边形ABED的面积为6,∴,即,
解得:x=﹣4(舍)或x=3,∴BF=3,
故选:B.
二、填空题
11、(2021·山东泰安市·九年级期末)如图:在中,点分别是的中点,连接,如果那么的周长是___.
【答案】30
【分析】根据三角形的中位线性质,求出AC的长,再求出ΔABC的周长.
【详解】∵点 D 、 E 分别是 AB 、 BC 的中点,∴DE是ΔABC的中位线,∴ DE=AC ,
∵ DE=2.5 ,∴ AC=5 ,∵ AB=13 , BC=12 ,∴ C△ABC=AB+BC+AC=13+12+5=30.故答案为:30.
12、(2019 达州)如图, ABCD的对角线AC、BD相交于点O,点E是AB的中点,△BEO的周长是8,则△BCD的周长为 .
【点拨】此题考查了平行四边形的性质,三角形中位线定理以及线段中点的定义.关键是掌握平行四边形的性质:①边:平行四边形的对边平行且相等.②角:平行四边形的对角相等;③对角线:平行四边形的对角线互相平分.
根据平行四边形的性质可得BO=DO=BD,进而可得OE是△ABC的中位线,由三角形中位线定理得出BC=2OE,再根据平行四边形的性质可得AB=CD,从而可得△BCD的周长=△BEO的周长×2.
【解析】解:∵ ABCD的对角线AC、BD相交于点O,
∴BO=DO=BD,BD=2OB,∴O为BD中点,
∵点E是AB的中点,∴AB=2BE,BC=2OE,
∵四边形ABCD是平行四边形,∴AB=CD,∴CD=2BE.
∵△BEO的周长为8,∴OB+OE+BE=8,
∴BD+BC+CD=2OB+2OE+2BE=2(OB+OE+BE)=16,∴△BCD的周长是16,
故答案为16.
13、如图,矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AC=8,则EF=________.
【答案】2
【考点】三角形中位线定理,矩形的性质
【解析】【解答】解:∵四边形ABCD为矩形,
∴BD=AC=8,
又∵矩形对角线的交点等分对角线,
∴OD=4,
又∵在△AOD中,EF为△AOD的中位线,
∴EF=2.
故答案为2.
14、(2021春 崇川区期末)已知菱形中,,连接,则等于
A. B. C. D.
【分析】由菱形的性质可得,,即可求解.
【解析】菱形中,,
,,
,
故选:.
15、(2020春 滨湖区期中)如图,在四边形ABCD中,点E、F分别是线段AD、BC的中点,G、H分别是线段BD、AC的中点,当四边形ABCD的边满足 时,四边形EGFH是菱形.
【思路点拨】本题可根据菱形的定义来求解.E、G分别是AD,BD的中点,那么EG就是三角形ADB的中位线,同理,HF是三角形ABC的中位线,因此EG、HF同时平行且相等于AB,因此EG∥HF,EG=HF,因此四边形EHFG是平行四边形,E、H是AD,AC的中点,那么EH=CD,要想证明EHFG是菱形,那么就需证明EG=EH,那么就需要AB、CD满足AB=CD的条件.
【答案】解:当AB=CD时,四边形EGFH是菱形.
∵点E,G分别是AD,BD的中点,∴EG∥AB,同理HF∥AB,∴EG∥HF,EG=HF=AB,
∴四边形EGFH是平行四边形.
∵EG=AB,又可同理证得EH=CD,
∵AB=CD,∴EG=EH,∴四边形EGFH是菱形.
故答案为AB=CD.
16、(2020春 常州期中)如图,正方形中,点、分别是、边上的点,且,垂足为点,的面积为,则图中阴影部分的面积为 .
【分析】证明得到,两个三角形的面积都减去的面积得到图中阴影部分的面积.
【解析】四边形为正方形,,,
,,
,,
在和中,,,
图中阴影部分的面积.
故答案为.
17、(2020春 曲阜市期末)如图,正方形ABCD的边长是2,对角线AC、BD相交于点O,点E、F分别在边AD、AB上,且OE⊥OF,则四边形AFOE的面积为 .
【点拨】证明△AOE≌△BOF(ASA),得出△AOE的面积=△BOF的面积,得出四边形AFOE的面积=正方形ABCD的面积=×22=1即可.
【解析】解:∵四边形ABD是正方形,∴OA=OB,∠OAE=∠OBF=45°,AC⊥BD,
∴∠AOB=90°,
∵OE⊥OF,∴∠EOF=90°,∴∠AOE=∠BOF,
在△AOE和△BOF中,,∴△AOE≌△BOF(ASA),
∴△AOE的面积=△BOF的面积,
∴四边形AFOE的面积=正方形ABCD的面积=×22=1;
故答案为:1.
18、如图,在中,,为的中线,过点作于点,过点作的平行线,交的延长线于点,在的延长线上截取,连接、.若,,则 .
【分析】首先可判断四边形是平行四边形,再由直角三角形斜边中线等于斜边一半,可得,则可判断四边形是菱形,设,则,,在中利用勾股定理可求出的值.
【解析】,,四边形是平行四边形,
,,
又点是中点,,四边形是菱形,
设,则,,
在中,,
,即,解得:,即.
故答案是:5.
三、解答题
19、如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图.
(1)以A点为旋转中心,将△ABC绕点A顺时针旋转90°得△AB1C1,画出△AB1C1;
(2)作出△ABC关于坐标原点O成中心对称的△A2B2C2.
【答案】(1)△AB 1C 1如图所示;见解析;(2)△A 2B 2C 2如图所示;见解析.
【分析】(1)依据△ABC绕点A顺时针旋转90°,即可得到△AB1C1;
(2)依据中心对称的性质进行作图,即可得到△ABC关于坐标原点O成中心对称的△A2B2C2.
【详解】(1)△AB 1C 1如图所示;
(2)△A 2B 2C 2如图所示.
20、如图所示平行四边形中,分别是边,上的点,且.
(1)求证:;
(2)连结,若,,求的度数.
【解】:(1)证明:在平行四边形中,,,
,
,
四边形是平行四边形
.
(2),
.
21、(2020·黑龙江大庆市·八年级期末)如图,四边形四条边上的中点分别为、、、,顺次连接、、、,得到四边形.求证:四边形是平行四边形.
【答案】见解析
【分析】连接AC,根据三角形的中位线定理得到,,同理推出,,根据一组对边平行且相等的四边形是平行四边形得出四边形EFGH是平行四边形
【详解】证明:连接AC.
是DC的中点,H是AD的中点,,且,
同理可知,且,,且,四边形是平行四边形.
22、(2020春 蔡甸区期中)如图,已知E,F是四边形ABCD的对角线BD的三等分点,CE,CF的延长线分别平分AB,AD.求证:四边形ABCD是平行四边形.
【分析】连接AC交BD于O,连接AE,AF,首先证得四边形AFCE是平行四边形得到AO=OC,然后证出OB=OD,利用对角线互相平分的四边形是平行四边形判定即可.
【解答】证明:连接AC交BD于O,连接AE,AF,如图所示:
∵G是AB中点,BE=EF∴GE是△ABF的一条中位线,∴EG∥AF,即CE∥AF,
同理:CF∥AE,
∴四边形AFCE是平行四边形.∴OA=OC,OE=OF,
又∵BE=DF,∴OB=OD,
∴四边形ABCD是平行四边形.
23、如图,将的边延长至点,使,连接,,,交于点
(1)求证:;
(2)若,求证:四边形是矩形.
【证明】:(1)四边形是平行四边形
,
,且,
(2)四边形是平行四边形
,,且
,,
四边形是平行四边形,
,
又,
是矩形
24、(2020春 博白县期末)如图,正方形ABCD边长为8,E,F分别是BC,CD上的点,且AE⊥BF.
(1)求证:AE=BF.
(2)若AF=10,求AE的长.
【点拨】(1)由正方形的性质可得∠ABC=90°=∠C,AB=BC,由余角的性质可得∠BAE=∠CBF,可证△ABE≌△BCF,可得AE=BF;
(2)由勾股定理可求DF=6,可得FC=2,由勾股定理可求AE=BF=2.
【解析】证明;(1)∵四边形ABCD是正方形,
∴∠ABC=90°=∠C,AB=BC,
∴∠ABF+∠CBF=90°,
∵AE⊥BF,
∴∠ABF+∠BAE=90°,
∴∠BAE=∠CBF,
∴△ABE≌△BCF(ASA),
∴AE=BF;
(2)∵AF=10,AD=8,
∴DF===6,
∴CF=8﹣6=2,
∴BF===2,
∴AE=2.
25、如图,在中,,是上任一点,且.
(1)若平分,求证:;
(2)若,且在中点时,试判断四边形的形状,并说明你的理由.
【解】:(1)证明:,.
又平分,.
.;
(2)四边形是正方形,理由如下:
,是 的中点,,即.
又,..
又且是的中点,..
,四边形是平行四边形.
,四边形是正方形.
26、(2020 朝阳区一模)如图,四边形ABCD是平行四边形,AE⊥BC,AF⊥CD,垂足分别为E,F,且BE=DF.
(1)求证:四边形ABCD是菱形;
(2)连接EF并延长,交AD的延长线于点G,若∠CEG=30°,AE=2,求EG的长.
【分析】(1)利用全等三角形的性质证明AB=AD即可解决问题;
(2)由直角三角形的性质可求解.
【详解】(1)证明:∵四边形ABCD是平行四边形,∴∠B=∠D,
∵AE⊥BC,AF⊥CD,∴∠AEB=∠AFD=90°,且BE=DF,∠B=∠D,
∴△AEB≌△AFD(AAS),∴AB=AD,∴四边形ABCD是菱形;
(2)如图,
∵AD∥BC,∴∠CEG=∠G=30°,
∵AE⊥BC,AD∥BC,∴∠EAG=90°,且∠G=30°,∴EG=2AE=4.
27、(2020 官渡区二模)如图,在平行四边形ABCD中,AC,BD交于点O,且AO=BO,∠ADB的平分线DE交AB于点E.
(1)求证:四边形ABCD是矩形.
(2)若AB=8,OC=5,求AE的长.
【点拨】(1)由平行四边形性质和已知条件得出AC=BD,即可得出结论;
(2)过点E作EG⊥BD于点G,先由角平分线的性质得出EG=EA,再证Rt△ADE≌Rt△GDE(HL)得AD=GD=6,在Rt△BEG中,由勾股定理得出方程,解方程即可.
【解析】(1)证明:∵四边形ABCD是平行四边形,∴AC=2AO,BD=2BO,
∵AO=BO,∴AC=BD,∴平行四边形ABCD为矩形;
(2)解:过点E作EG⊥BD于点G,如图所示:
∵四边形ABCD是矩形,OC=5,∴∠BAD=90°,BD=AC=2OC=10.
在Rt△ABD中,AB=8,BD=10,∴AD===6,
∵∠DAB=90°,∴EA⊥AD,
∵DE为∠ADB的平分线,EG⊥BD,∴EG=EA,∠EGB=90°.
在Rt△ADE和Rt△GDE中,,∴Rt△ADE≌Rt△GDE(HL),∴AD=GD=6,
∴BG=BD﹣GD=10﹣6=4,
在Rt△BEG中,由勾股定理得:BE2=EG2+BG2,即(8﹣AE)2=AE2+42,解得:AE=3.
2021-2022学年苏科版八年级数学下册
一、选择题
1、(2020秋 盘龙区期末)我国民间,流传着许多含有吉祥意义的文字图案,表示对幸福生活的向往,良辰佳节的祝贺.比如下列图案分别表示“福”、“禄”、“寿”、“喜”,其中是中心对称图形的是( )
A.①③ B.①④ C.②③ D.②④
2、(2021·广东广州市·八年级期末)如图,在四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )
A.AB∥CD,AD∥BC B.AD∥BC,AB=CD
C.OA=OC,OB=OD D.AB=CD,AD=BC
3、(2020秋 朝阳区校级月考)如图,在 ABCD中,已知AC=4cm,若△ACD的周长为14cm,则 ABCD的周长为( )
A.14cm B.28cm C.10cm D.20cm
4、如图,在菱形ABCD中,对角线AC,BD相交于点O,AC=8,BD=6,点E,F分别为AO,DO的中点,则线段EF的长为( )
A.2.5 B.3 C.4 D.5
5、如图,在中,,将绕点按逆时针方向旋转得到△.若点恰好落在边上,且,则的度数为
A. B. C. D.
6、如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=2,则矩形的对角线AC的长是( )
A.2 B.4 C.2 D.4
7、如图,下列条件不能判定四边形ABCD是矩形的是( )
A.∠DAB=∠ABC=∠BCD=90° B.AB∥CD,AB=CD,AB⊥AD
C.AO=BO,CO=DO D.AO=BO=CO=DO
8、如图,四边形ABCD的对角线互相平分,要使它变为菱形,需要添加的条件是( )
A.AB=CD B.AD=BC C.AC=BD D.AB=BC
9、(2020春 温州期中)如图,菱形ABCD的对角线相交于点O,AC=12,BD=16,点P为边BC上一点,且P不与B、C重合.过P作PE⊥AC于E,PF⊥BD于F,连结EF,则EF的最小值为( )
A.4 B.4.8 C.5 D.6
10、如图,点M是正方形ABCD边CD上一点,连接AM,作DE⊥AM于点F,连接BE.若AF=1,四边形ABED的面积为6,则BF的长为( )
A.2 B.3 C. D.
二、填空题
11、(2021·山东泰安市·九年级期末)如图:在中,点分别是的中点,连接,如果那么的周长是___.
12、(2019 达州)如图, ABCD的对角线AC、BD相交于点O,点E是AB的中点,△BEO的周长是8,则△BCD的周长为 .
13、如图,矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AC=8,则EF=________.
14、(2021春 崇川区期末)已知菱形中,,连接,则等于
A. B. C. D.
15、(2020春 滨湖区期中)如图,在四边形ABCD中,点E、F分别是线段AD、BC的中点,G、H分别是线段BD、AC的中点,当四边形ABCD的边满足 时,四边形EGFH是菱形.
16、(2020春 常州期中)如图,正方形中,点、分别是、边上的点,且,垂足为点,的面积为,则图中阴影部分的面积为 .
17、(2020春 曲阜市期末)如图,正方形ABCD的边长是2,对角线AC、BD相交于点O,点E、F分别在边AD、AB上,且OE⊥OF,则四边形AFOE的面积为 .
18、如图,在中,,为的中线,过点作于点,过点作的平行线,交的延长线于点,在的延长线上截取,连接、.若,,则 .
三、解答题
19、如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图.
(1)以A点为旋转中心,将△ABC绕点A顺时针旋转90°得△AB1C1,画出△AB1C1;
(2)作出△ABC关于坐标原点O成中心对称的△A2B2C2.
20、如图所示平行四边形中,分别是边,上的点,且.
(1)求证:;
(2)连结,若,,求的度数.
21、(2020·黑龙江大庆市·八年级期末)如图,四边形四条边上的中点分别为、、、,顺次连接、、、,得到四边形.求证:四边形是平行四边形.
22、(2020春 蔡甸区期中)如图,已知E,F是四边形ABCD的对角线BD的三等分点,CE,CF的延长线分别平分AB,AD.求证:四边形ABCD是平行四边形.
23、如图,将的边延长至点,使,连接,,,交于点
(1)求证:;
(2)若,求证:四边形是矩形.
24、(2020春 博白县期末)如图,正方形ABCD边长为8,E,F分别是BC,CD上的点,且AE⊥BF.
(1)求证:AE=BF.
(2)若AF=10,求AE的长.
25、如图,在中,,是上任一点,且.
(1)若平分,求证:;
(2)若,且在中点时,试判断四边形的形状,并说明你的理由.
26、(2020 朝阳区一模)如图,四边形ABCD是平行四边形,AE⊥BC,AF⊥CD,垂足分别为E,F,且BE=DF.
(1)求证:四边形ABCD是菱形;
(2)连接EF并延长,交AD的延长线于点G,若∠CEG=30°,AE=2,求EG的长.
27、(2020 官渡区二模)如图,在平行四边形ABCD中,AC,BD交于点O,且AO=BO,∠ADB的平分线DE交AB于点E.
(1)求证:四边形ABCD是矩形.
(2)若AB=8,OC=5,求AE的长.
第9章 中心对称图形—平行四边形 单元整合练习题(基础)
2021-2022学年苏科版八年级数学下册(解析)
一、选择题
1、(2020秋 盘龙区期末)我国民间,流传着许多含有吉祥意义的文字图案,表示对幸福生活的向往,良辰佳节的祝贺.比如下列图案分别表示“福”、“禄”、“寿”、“喜”,其中是中心对称图形的是( )
A.①③ B.①④ C.②③ D.②④
【点拨】根据中心对称图形的定义,结合选项所给图形进行判断即可.
【解析】解:①不是中心对称图形,故本选项不合题意;
②是中心对称图形,故本选项符合题意;
③不是中心对称图形,故本选项不合题意;
④是中心对称图形,故本选项符合题意;
故选:D.
2、(2021·广东广州市·八年级期末)如图,在四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )
A.AB∥CD,AD∥BC B.AD∥BC,AB=CD
C.OA=OC,OB=OD D.AB=CD,AD=BC
【答案】B
【分析】根据平行四边形的判定方法即可判断.
【详解】A、根据两组对边分别平行的四边形是平行四边形,可以判定;
B、无法判定,四边形可能是等腰梯形,也可能是平行四边形;
C、根据对角线互相平分的四边形是平行四边形,可以判定;
D、根据两组对边分别相等的四边形是平行四边形,可以判定;故选:B.
3、(2020秋 朝阳区校级月考)如图,在 ABCD中,已知AC=4cm,若△ACD的周长为14cm,则 ABCD的周长为( )
A.14cm B.28cm C.10cm D.20cm
【点拨】先根据AC=4cm,△ACD的周长为14cm得出AD+CD=10cm,再结合四边形ABCD是平行四边形知AB=CD、BC=AD,从而得出答案.
【解析】解:∵△ACD的周长为14cm,即AD+CD+AC=14cm,且AC=4cm,
∴AD+CD=10cm,
∵四边形ABCD是平行四边形,
∴AB=CD、BC=AD,
则 ABCD的周长为AB+BC+AD+CD=10+10=20(cm),
故选:D.
4、如图,在菱形ABCD中,对角线AC,BD相交于点O,AC=8,BD=6,点E,F分别为AO,DO的中点,则线段EF的长为( )
A.2.5 B.3 C.4 D.5
【分析】本题考查了菱形的性质、勾股定理、三角形的中位线定理,利用勾股定理求得AD的长是解题的关键.
先依据菱形的性质求得OA、OD的长,然后依据勾股定理可求得AD的长,最后依据三角形中位线定理求的EF的长即可.
【解答】解:∵四边形ABCD为菱形,
∴AC⊥BD,OA=OC=AC=4,OB=OD=BD=3.
在Rt△AOD中,依据勾股定理可知:AD===5.
∵点E,F分别为AO,DO的中点,
∴EF是△AOD的中位线,
∴EF=AD=2.5;
故选:A.
5、如图,在中,,将绕点按逆时针方向旋转得到△.若点恰好落在边上,且,则的度数为
A. B. C. D.
【分析】由旋转的性质可得,,由等腰三角形的性质可得,,由三角形的外角性质和三角形内角和定理可求解.
【解析】,
,
,
将绕点按逆时针方向旋转得到△,
,,
,
,
,
,
,
故选:.
6、如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=2,则矩形的对角线AC的长是( )
A.2 B.4 C.2 D.4
【答案】B
【解析】∵四边形ABCD是矩形,∴OA=OC=OB=OD.∴△OAB是等腰三角形.
∵∠AOB=60° ,∴△OAB是等边三角形,∴AB=OA.
∵AB=2,AB=OA,∴OA=2.
∵OA=OC,OA=2,∴AC=4.
故选B.
7、如图,下列条件不能判定四边形ABCD是矩形的是( )
A.∠DAB=∠ABC=∠BCD=90° B.AB∥CD,AB=CD,AB⊥AD
C.AO=BO,CO=DO D.AO=BO=CO=DO
解;A、∠DAB=∠ABC=∠BCD=90°根据有三个角是直角的四边形是矩形可判定为矩形,故此选项错误;
B、AB∥CD,AB=CD,可以判定为平行四边形,又有AB⊥AD,可判定为矩形,故此选项错误;
C、AO=BO,CO=DO,不可以判定为平行四边形,所以不可判定为矩形,故此选项正确;
D、AO=BO=CO=DO,可以得到对角线互相平分且相等,据此可以判定矩形,故此选项错误.
故选:C.
8、如图,四边形ABCD的对角线互相平分,要使它变为菱形,需要添加的条件是( )
A.AB=CD B.AD=BC C.AC=BD D.AB=BC
【思路点拨】由已知条件得出四边形ABCD是平行四边形,再由一组邻边相等,即可得出四边形ABCD是菱形.
【答案】解:需要添加的条件是AB=BC;
理由如下:
∵四边形ABCD的对角线互相平分,
∴四边形ABCD是平行四边形,
∵AB=BC,
∴平行四边形ABCD是菱形(一组邻边相等的平行四边形是菱形);
故选:D.
9、(2020春 温州期中)如图,菱形ABCD的对角线相交于点O,AC=12,BD=16,点P为边BC上一点,且P不与B、C重合.过P作PE⊥AC于E,PF⊥BD于F,连结EF,则EF的最小值为( )
A.4 B.4.8 C.5 D.6
【思路点拨】由菱形的性质可得AC⊥BD,BO=BD=8,OC=AC=6,由勾股定理可求BC的长,可证四边形OEPF是矩形,可得EF=OP,OP⊥BC时,OP有最小值,由面积法可求解.
【答案】解:连接OP,
∵四边形ABCD是菱形,AC=12,BD=16,
∴AC⊥BD,BO=BD=8,OC=AC=6,∴BC===10,
∵PE⊥AC,PF⊥BD,AC⊥BD,∴四边形OEPF是矩形,∴FE=OP,
∵当OP⊥BC时,OP有最小值,此时S△OBC=OB×OC=BC×OP,
∴OP==4.8,∴EF的最小值为4.8,
故选:B.
10、如图,点M是正方形ABCD边CD上一点,连接AM,作DE⊥AM于点F,连接BE.若AF=1,四边形ABED的面积为6,则BF的长为( )
A.2 B.3 C. D.
【点拨】证明△ABF≌△DAE得BF=AF,AF=DE,进而由已知四边形的面积列出BF的方程进行解答便可.
【解析】解:∵四边形ABCD是正方形,∴AB=AD,∠BAD=90°,
∵BF⊥AM,∴∠ABF+∠BAF=∠BAF+∠DAE=90°,∴∠ABF=∠DAE,
∵DE⊥AM,∴∠AFB=∠DEA=90°,∴△ABF≌△DAE(AAS),
∴BF=AE,AF=DE=1,
设BF=AE=x,则EF=x﹣1,
∵四边形ABED的面积为6,∴,即,
解得:x=﹣4(舍)或x=3,∴BF=3,
故选:B.
二、填空题
11、(2021·山东泰安市·九年级期末)如图:在中,点分别是的中点,连接,如果那么的周长是___.
【答案】30
【分析】根据三角形的中位线性质,求出AC的长,再求出ΔABC的周长.
【详解】∵点 D 、 E 分别是 AB 、 BC 的中点,∴DE是ΔABC的中位线,∴ DE=AC ,
∵ DE=2.5 ,∴ AC=5 ,∵ AB=13 , BC=12 ,∴ C△ABC=AB+BC+AC=13+12+5=30.故答案为:30.
12、(2019 达州)如图, ABCD的对角线AC、BD相交于点O,点E是AB的中点,△BEO的周长是8,则△BCD的周长为 .
【点拨】此题考查了平行四边形的性质,三角形中位线定理以及线段中点的定义.关键是掌握平行四边形的性质:①边:平行四边形的对边平行且相等.②角:平行四边形的对角相等;③对角线:平行四边形的对角线互相平分.
根据平行四边形的性质可得BO=DO=BD,进而可得OE是△ABC的中位线,由三角形中位线定理得出BC=2OE,再根据平行四边形的性质可得AB=CD,从而可得△BCD的周长=△BEO的周长×2.
【解析】解:∵ ABCD的对角线AC、BD相交于点O,
∴BO=DO=BD,BD=2OB,∴O为BD中点,
∵点E是AB的中点,∴AB=2BE,BC=2OE,
∵四边形ABCD是平行四边形,∴AB=CD,∴CD=2BE.
∵△BEO的周长为8,∴OB+OE+BE=8,
∴BD+BC+CD=2OB+2OE+2BE=2(OB+OE+BE)=16,∴△BCD的周长是16,
故答案为16.
13、如图,矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AC=8,则EF=________.
【答案】2
【考点】三角形中位线定理,矩形的性质
【解析】【解答】解:∵四边形ABCD为矩形,
∴BD=AC=8,
又∵矩形对角线的交点等分对角线,
∴OD=4,
又∵在△AOD中,EF为△AOD的中位线,
∴EF=2.
故答案为2.
14、(2021春 崇川区期末)已知菱形中,,连接,则等于
A. B. C. D.
【分析】由菱形的性质可得,,即可求解.
【解析】菱形中,,
,,
,
故选:.
15、(2020春 滨湖区期中)如图,在四边形ABCD中,点E、F分别是线段AD、BC的中点,G、H分别是线段BD、AC的中点,当四边形ABCD的边满足 时,四边形EGFH是菱形.
【思路点拨】本题可根据菱形的定义来求解.E、G分别是AD,BD的中点,那么EG就是三角形ADB的中位线,同理,HF是三角形ABC的中位线,因此EG、HF同时平行且相等于AB,因此EG∥HF,EG=HF,因此四边形EHFG是平行四边形,E、H是AD,AC的中点,那么EH=CD,要想证明EHFG是菱形,那么就需证明EG=EH,那么就需要AB、CD满足AB=CD的条件.
【答案】解:当AB=CD时,四边形EGFH是菱形.
∵点E,G分别是AD,BD的中点,∴EG∥AB,同理HF∥AB,∴EG∥HF,EG=HF=AB,
∴四边形EGFH是平行四边形.
∵EG=AB,又可同理证得EH=CD,
∵AB=CD,∴EG=EH,∴四边形EGFH是菱形.
故答案为AB=CD.
16、(2020春 常州期中)如图,正方形中,点、分别是、边上的点,且,垂足为点,的面积为,则图中阴影部分的面积为 .
【分析】证明得到,两个三角形的面积都减去的面积得到图中阴影部分的面积.
【解析】四边形为正方形,,,
,,
,,
在和中,,,
图中阴影部分的面积.
故答案为.
17、(2020春 曲阜市期末)如图,正方形ABCD的边长是2,对角线AC、BD相交于点O,点E、F分别在边AD、AB上,且OE⊥OF,则四边形AFOE的面积为 .
【点拨】证明△AOE≌△BOF(ASA),得出△AOE的面积=△BOF的面积,得出四边形AFOE的面积=正方形ABCD的面积=×22=1即可.
【解析】解:∵四边形ABD是正方形,∴OA=OB,∠OAE=∠OBF=45°,AC⊥BD,
∴∠AOB=90°,
∵OE⊥OF,∴∠EOF=90°,∴∠AOE=∠BOF,
在△AOE和△BOF中,,∴△AOE≌△BOF(ASA),
∴△AOE的面积=△BOF的面积,
∴四边形AFOE的面积=正方形ABCD的面积=×22=1;
故答案为:1.
18、如图,在中,,为的中线,过点作于点,过点作的平行线,交的延长线于点,在的延长线上截取,连接、.若,,则 .
【分析】首先可判断四边形是平行四边形,再由直角三角形斜边中线等于斜边一半,可得,则可判断四边形是菱形,设,则,,在中利用勾股定理可求出的值.
【解析】,,四边形是平行四边形,
,,
又点是中点,,四边形是菱形,
设,则,,
在中,,
,即,解得:,即.
故答案是:5.
三、解答题
19、如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图.
(1)以A点为旋转中心,将△ABC绕点A顺时针旋转90°得△AB1C1,画出△AB1C1;
(2)作出△ABC关于坐标原点O成中心对称的△A2B2C2.
【答案】(1)△AB 1C 1如图所示;见解析;(2)△A 2B 2C 2如图所示;见解析.
【分析】(1)依据△ABC绕点A顺时针旋转90°,即可得到△AB1C1;
(2)依据中心对称的性质进行作图,即可得到△ABC关于坐标原点O成中心对称的△A2B2C2.
【详解】(1)△AB 1C 1如图所示;
(2)△A 2B 2C 2如图所示.
20、如图所示平行四边形中,分别是边,上的点,且.
(1)求证:;
(2)连结,若,,求的度数.
【解】:(1)证明:在平行四边形中,,,
,
,
四边形是平行四边形
.
(2),
.
21、(2020·黑龙江大庆市·八年级期末)如图,四边形四条边上的中点分别为、、、,顺次连接、、、,得到四边形.求证:四边形是平行四边形.
【答案】见解析
【分析】连接AC,根据三角形的中位线定理得到,,同理推出,,根据一组对边平行且相等的四边形是平行四边形得出四边形EFGH是平行四边形
【详解】证明:连接AC.
是DC的中点,H是AD的中点,,且,
同理可知,且,,且,四边形是平行四边形.
22、(2020春 蔡甸区期中)如图,已知E,F是四边形ABCD的对角线BD的三等分点,CE,CF的延长线分别平分AB,AD.求证:四边形ABCD是平行四边形.
【分析】连接AC交BD于O,连接AE,AF,首先证得四边形AFCE是平行四边形得到AO=OC,然后证出OB=OD,利用对角线互相平分的四边形是平行四边形判定即可.
【解答】证明:连接AC交BD于O,连接AE,AF,如图所示:
∵G是AB中点,BE=EF∴GE是△ABF的一条中位线,∴EG∥AF,即CE∥AF,
同理:CF∥AE,
∴四边形AFCE是平行四边形.∴OA=OC,OE=OF,
又∵BE=DF,∴OB=OD,
∴四边形ABCD是平行四边形.
23、如图,将的边延长至点,使,连接,,,交于点
(1)求证:;
(2)若,求证:四边形是矩形.
【证明】:(1)四边形是平行四边形
,
,且,
(2)四边形是平行四边形
,,且
,,
四边形是平行四边形,
,
又,
是矩形
24、(2020春 博白县期末)如图,正方形ABCD边长为8,E,F分别是BC,CD上的点,且AE⊥BF.
(1)求证:AE=BF.
(2)若AF=10,求AE的长.
【点拨】(1)由正方形的性质可得∠ABC=90°=∠C,AB=BC,由余角的性质可得∠BAE=∠CBF,可证△ABE≌△BCF,可得AE=BF;
(2)由勾股定理可求DF=6,可得FC=2,由勾股定理可求AE=BF=2.
【解析】证明;(1)∵四边形ABCD是正方形,
∴∠ABC=90°=∠C,AB=BC,
∴∠ABF+∠CBF=90°,
∵AE⊥BF,
∴∠ABF+∠BAE=90°,
∴∠BAE=∠CBF,
∴△ABE≌△BCF(ASA),
∴AE=BF;
(2)∵AF=10,AD=8,
∴DF===6,
∴CF=8﹣6=2,
∴BF===2,
∴AE=2.
25、如图,在中,,是上任一点,且.
(1)若平分,求证:;
(2)若,且在中点时,试判断四边形的形状,并说明你的理由.
【解】:(1)证明:,.
又平分,.
.;
(2)四边形是正方形,理由如下:
,是 的中点,,即.
又,..
又且是的中点,..
,四边形是平行四边形.
,四边形是正方形.
26、(2020 朝阳区一模)如图,四边形ABCD是平行四边形,AE⊥BC,AF⊥CD,垂足分别为E,F,且BE=DF.
(1)求证:四边形ABCD是菱形;
(2)连接EF并延长,交AD的延长线于点G,若∠CEG=30°,AE=2,求EG的长.
【分析】(1)利用全等三角形的性质证明AB=AD即可解决问题;
(2)由直角三角形的性质可求解.
【详解】(1)证明:∵四边形ABCD是平行四边形,∴∠B=∠D,
∵AE⊥BC,AF⊥CD,∴∠AEB=∠AFD=90°,且BE=DF,∠B=∠D,
∴△AEB≌△AFD(AAS),∴AB=AD,∴四边形ABCD是菱形;
(2)如图,
∵AD∥BC,∴∠CEG=∠G=30°,
∵AE⊥BC,AD∥BC,∴∠EAG=90°,且∠G=30°,∴EG=2AE=4.
27、(2020 官渡区二模)如图,在平行四边形ABCD中,AC,BD交于点O,且AO=BO,∠ADB的平分线DE交AB于点E.
(1)求证:四边形ABCD是矩形.
(2)若AB=8,OC=5,求AE的长.
【点拨】(1)由平行四边形性质和已知条件得出AC=BD,即可得出结论;
(2)过点E作EG⊥BD于点G,先由角平分线的性质得出EG=EA,再证Rt△ADE≌Rt△GDE(HL)得AD=GD=6,在Rt△BEG中,由勾股定理得出方程,解方程即可.
【解析】(1)证明:∵四边形ABCD是平行四边形,∴AC=2AO,BD=2BO,
∵AO=BO,∴AC=BD,∴平行四边形ABCD为矩形;
(2)解:过点E作EG⊥BD于点G,如图所示:
∵四边形ABCD是矩形,OC=5,∴∠BAD=90°,BD=AC=2OC=10.
在Rt△ABD中,AB=8,BD=10,∴AD===6,
∵∠DAB=90°,∴EA⊥AD,
∵DE为∠ADB的平分线,EG⊥BD,∴EG=EA,∠EGB=90°.
在Rt△ADE和Rt△GDE中,,∴Rt△ADE≌Rt△GDE(HL),∴AD=GD=6,
∴BG=BD﹣GD=10﹣6=4,
在Rt△BEG中,由勾股定理得:BE2=EG2+BG2,即(8﹣AE)2=AE2+42,解得:AE=3.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
