2021-2022学年湘教版八年级数学下册2.6菱形同步达标测试题(Word版含答案)
文档属性
| 名称 | 2021-2022学年湘教版八年级数学下册2.6菱形同步达标测试题(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 306.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-19 21:08:53 | ||
图片预览


文档简介
2021-2022学年湘教版八年级数学下册《2-6菱形》同步达标测试题(附答案)
一.选择题(共8小题,满分40分)
1.菱形的对角线长分别是6和8,那么其边长是( )
A.5 B.10 C.20 D.40
2.关于菱形,下列说法错误的是( )
A.对角线互相平分 B.对角线互相垂直
C.四条边相等 D.对角线相等
3.如图,点P,Q分别是菱形ABCD的边AD,BC上的两个动点,若线段PQ长的最大值为8,最小值为8,则菱形ABCD的边长为( )
A.4 B.10 C.12 D.16
4.如图,在菱形ABCD中,M,N分别在AB,CD上,且AM=CN,MN与AC交于点O,连接BO.若∠DAC=26°,则∠OBC的度数为( )
A.54° B.64° C.74° D.26°
5.如图,已知菱形ABCD中,过AD中点E作EF⊥BD,交对角线BD于点M,交BC的延长线于点F.连接DF.若CF=2,则AB的长是( )
A.3 B.4 C.4 D.2
6.如图, ABCD中,AB=5a,BC=4a,∠A=60°,平行四边形内放着两个菱形,菱形DEFG和菱形BHIL,它们的重叠部分是平行四边形IJFK.已知三个阴影平行四边形的周长相等,那么平行四边形IJFK的面积为( )
A.a2 B.2a2 C. D.
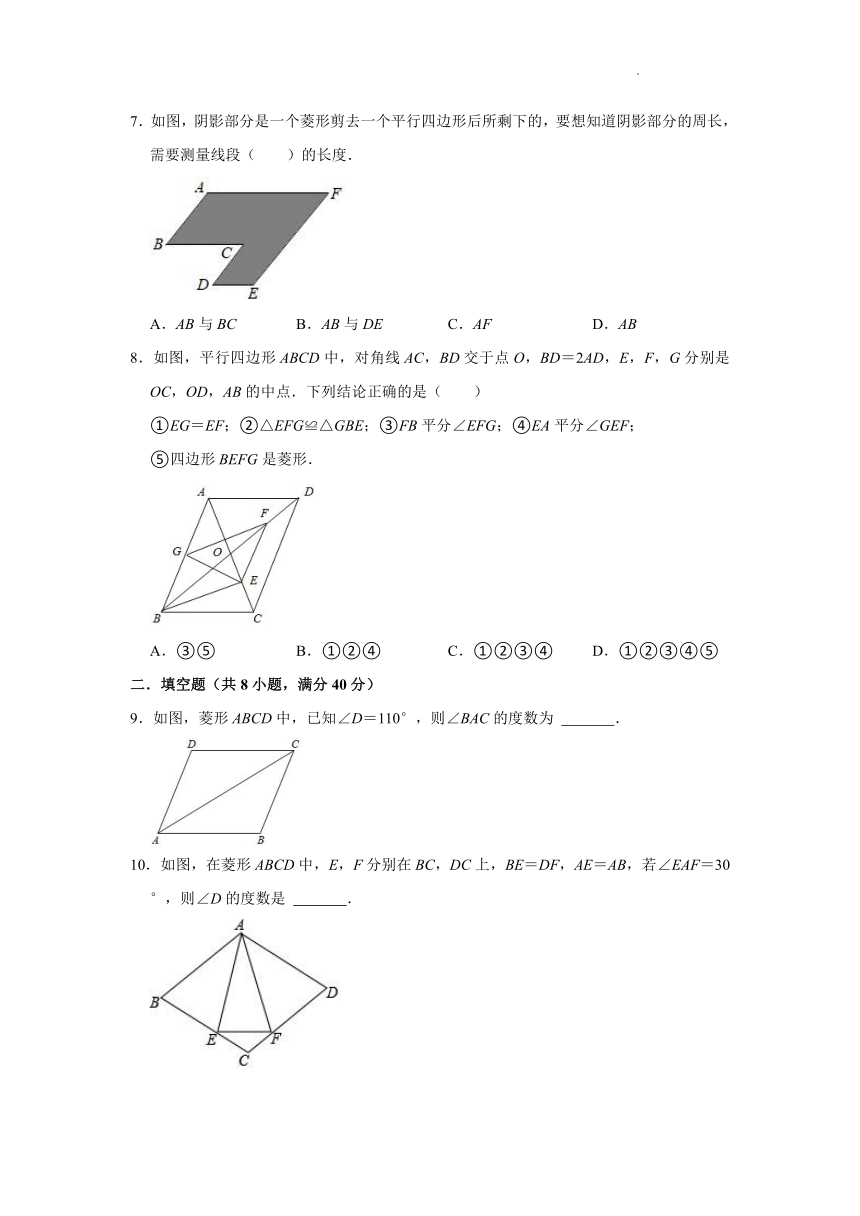
7.如图,阴影部分是一个菱形剪去一个平行四边形后所剩下的,要想知道阴影部分的周长,需要测量线段( )的长度.
A.AB与BC B.AB与DE C.AF D.AB
8.如图,平行四边形ABCD中,对角线AC,BD交于点O,BD=2AD,E,F,G分别是OC,OD,AB的中点.下列结论正确的是( )
①EG=EF;②△EFG≌△GBE;③FB平分∠EFG;④EA平分∠GEF;
⑤四边形BEFG是菱形.
A.③⑤ B.①②④ C.①②③④ D.①②③④⑤
二.填空题(共8小题,满分40分)
9.如图,菱形ABCD中,已知∠D=110°,则∠BAC的度数为 .
10.如图,在菱形ABCD中,E,F分别在BC,DC上,BE=DF,AE=AB,若∠EAF=30°,则∠D的度数是 .
11.如图,四边形ABCD为菱形,对角线AC,BD相交于点O,DH⊥AB于点H,连接OH,∠CAD=25°,则∠DHO的度数是 .
12.如图,菱形ABCD中,对角线AC=8,BD=6,BE⊥CD,则BE= .
13.如图,在边长为10的菱形ABCD中,对角线BD=16,点O是线段BD上的动点,OE⊥AB于E,OF⊥AD于F.则OE+OF= .
14.如图,菱形ABCD的对角线AC,BD相交于点O,过点O作OE⊥BC于点E,若AC=6,BD=8,则OE= .
15.如图,在菱形ABCD中,AC=6,AB=5,点E是直线AB、CD之间任意一点,连接AE、BE、DE、CE,则△EAB和△ECD的面积和等于 .
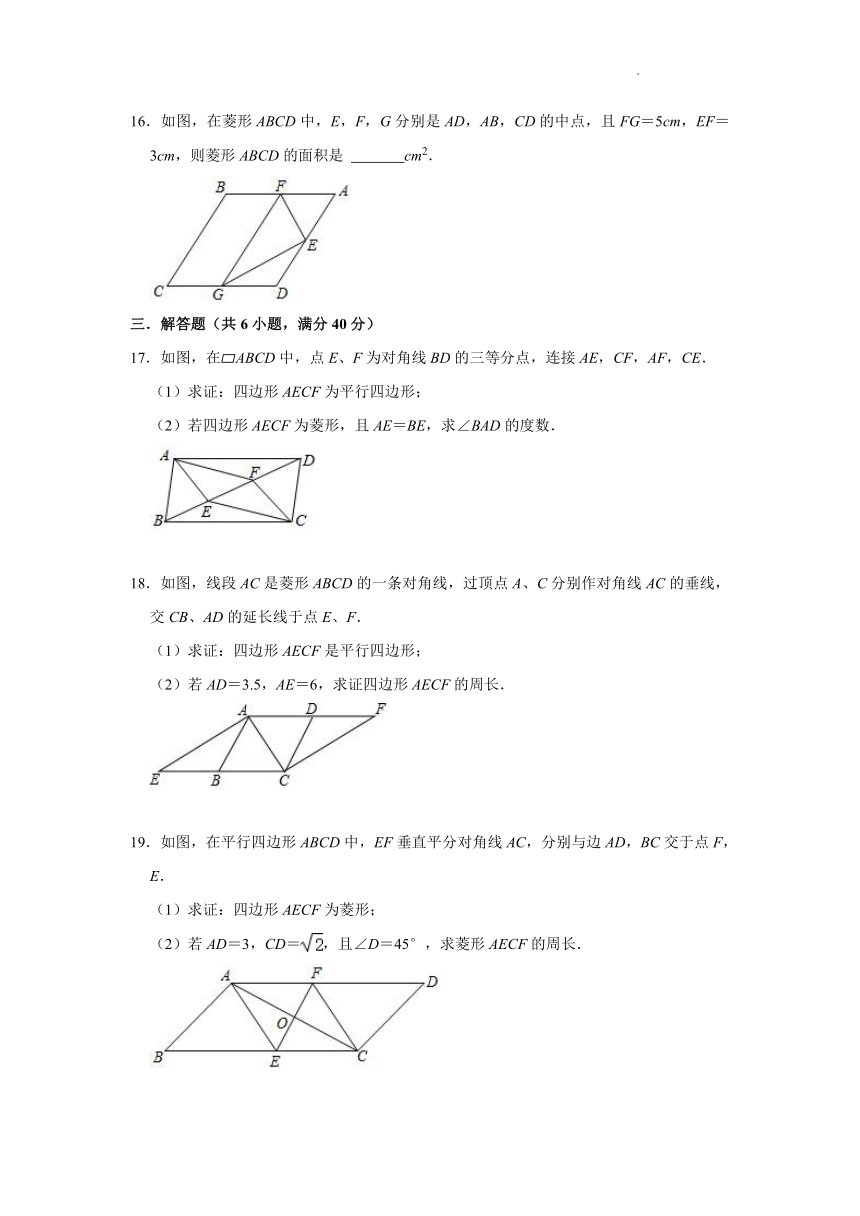
16.如图,在菱形ABCD中,E,F,G分别是AD,AB,CD的中点,且FG=5cm,EF=3cm,则菱形ABCD的面积是 cm2.
三.解答题(共6小题,满分40分)
17.如图,在 ABCD中,点E、F为对角线BD的三等分点,连接AE,CF,AF,CE.
(1)求证:四边形AECF为平行四边形;
(2)若四边形AECF为菱形,且AE=BE,求∠BAD的度数.
18.如图,线段AC是菱形ABCD的一条对角线,过顶点A、C分别作对角线AC的垂线,交CB、AD的延长线于点E、F.
(1)求证:四边形AECF是平行四边形;
(2)若AD=3.5,AE=6,求证四边形AECF的周长.
19.如图,在平行四边形ABCD中,EF垂直平分对角线AC,分别与边AD,BC交于点F,E.
(1)求证:四边形AECF为菱形;
(2)若AD=3,CD=,且∠D=45°,求菱形AECF的周长.
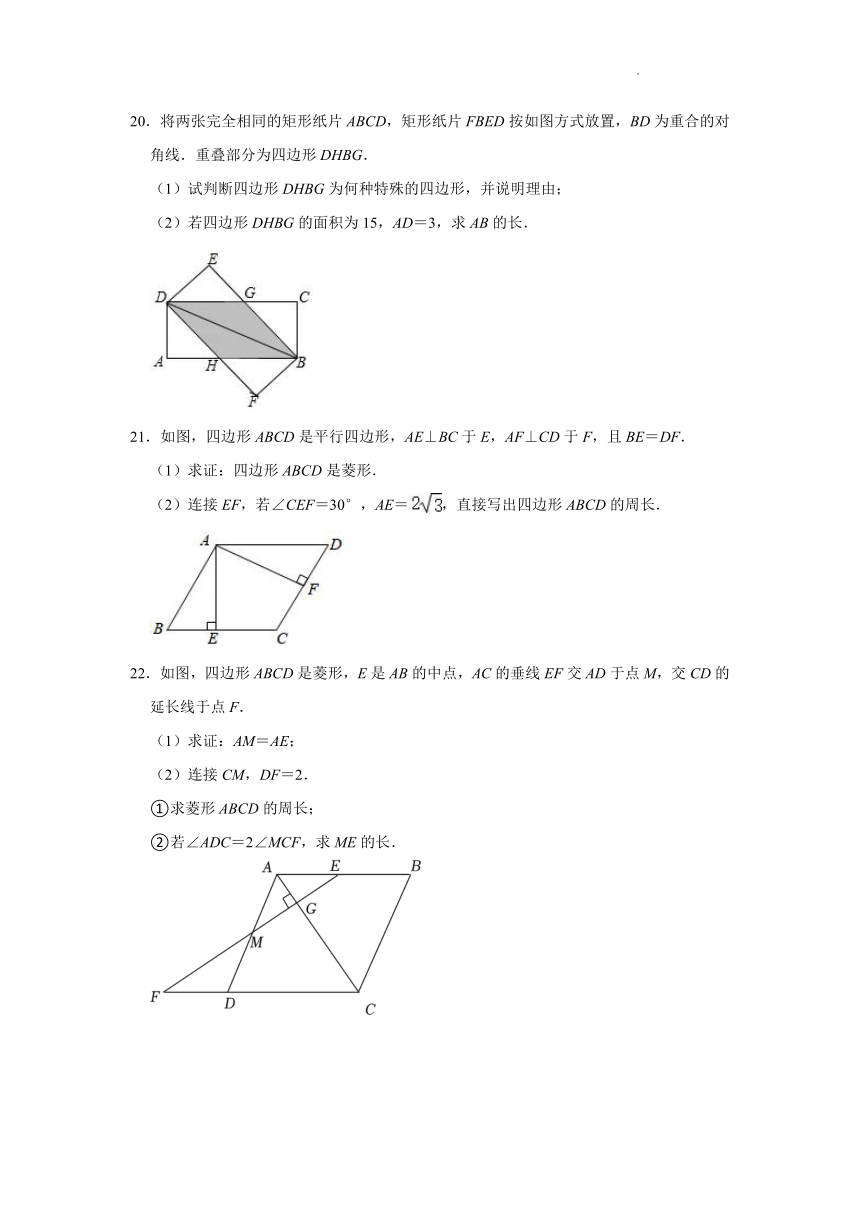
20.将两张完全相同的矩形纸片ABCD,矩形纸片FBED按如图方式放置,BD为重合的对角线.重叠部分为四边形DHBG.
(1)试判断四边形DHBG为何种特殊的四边形,并说明理由;
(2)若四边形DHBG的面积为15,AD=3,求AB的长.
21.如图,四边形ABCD是平行四边形,AE⊥BC于E,AF⊥CD于F,且BE=DF.
(1)求证:四边形ABCD是菱形.
(2)连接EF,若∠CEF=30°,AE=,直接写出四边形ABCD的周长.
22.如图,四边形ABCD是菱形,E是AB的中点,AC的垂线EF交AD于点M,交CD的延长线于点F.
(1)求证:AM=AE;
(2)连接CM,DF=2.
①求菱形ABCD的周长;
②若∠ADC=2∠MCF,求ME的长.
参考答案
一.选择题(共8小题,满分40分)
1.解:如图,菱形ABCD中,BD=8,AC=6,
则AC⊥BD,OB=4,OA=3,
∴AB=,
故选:A.
2.解:∵菱形的性质有四边相等,对角线互相垂直平分,
∴对角线相等不是菱形的性质,
故选:D.
3.解:如图,过点C作CH⊥AB,交AB的延长线于H,
∵四边形ABCD是菱形,
∴AD=AB=BC,
∵点P,Q分别是菱形ABCD的边AD,BC上的两个动点,
∴当点P与点A重合,点Q与点C重合时,PQ有最大值,即AC=8,
当PQ⊥BC时,PQ有最小值,即直线CD,直线AB的距离为8,即CH=8,
∴AH===16,
∵BC2=CH2+BH2,
∴BC2=(16﹣BC)2+64,
∴BC=10,
故选:B.
4.解:∵四边形ABCD为菱形,
∴AB∥CD,AB=BC,
∴∠MAO=∠NCO,∠AMO=∠CNO,
在△AMO和△CNO中,
,
∴△AMO≌△CNO(ASA),
∴AO=CO,
∵AB=BC,
∴BO⊥AC,
∴∠BOC=90°,
∵∠DAC=26°,
∴∠BCA=∠DAC=26°,
∴∠OBC=90°﹣26°=64°.
故选:B.
5.解:设CD与EF的交点为H,
∵四边形ABCD是菱形,
∴AD=CD=BC,∠ADB=∠CDB,
∵点E是AD中点,
∴AE=DE=AD,
在△DEM和△DHM中,
,
∴△DEM≌△DHM(ASA),
∴DE=DH,
∴DH=CH,
∵AD∥BC,
∴DE=CF=2,
∴AD=4=CD=BC=AB.
故选:C.
6.解:由题意 ABCD的周长为2(AB+BC)=18a,
又∵三个阴影平行四边形的周长相等,
∴由平移的性质可得: EALJ的周长= IJFK的周长= GKHC的周长=×18a=6a,
∴IJ+JF=EJ+JL=GK+KH=3a,
∴HI=IK+KH=3a,DG=EJ+JF=3a,
∴DG=HI,
∴IJ+JL+JF+EJ=6a,IJ+KH+GK+JF=6a,
又∵AB=5a,BC=4a,且四边形DEFG和四边形BHIL是菱形,
∴EF=IL=3a,AE=JF=a,IJ=2a,∠IJF=∠DEF=∠A=60°,
过点I作IP⊥EF,
∴在Rt△IJP中,
JP=IJ=a,IP==a,
∴平行四边形IJFK的面积为JF IP=a2,
故选:D.
7.解:如图,延长AB,ED交于点H,
∵四边形BCDH是平行四边形,
∴BC=DH,CD=BH,
∵四边形AFEH是菱形,
∴AF=EF=EH=AH,
∴阴影部分的周长=AB+BC+CD+DE+EF+EF=4AF,
故需要测量AF的长度,
故选:C.
8.解:设GF和AC的交点为点P,如图:
∵E、F分别是OC、OD的中点,
∴EF∥CD,且EF=CD,
∵四边形ABCD为平行四边形,
∴AB∥CD,且AB=CD,
∴∠FEG=∠BGE,
∵点G为AB的中点,
∴BG=AB=CD=FE,
在△EFG和△GBE中,,
∴△EFG≌△GBE(SAS),即②正确,
∴∠EGF=∠GEB,GF=BE,
∴GF∥BE,
∵BD=2BC,点O为平行四边形对角线交点,
∴BO=BD=BC,
∵E为OC中点,
∴BE⊥OC,
∴GP⊥AC,
∴∠APG=∠EPG=90°
∵GP∥BE,G为AB中点,
∴P为AE中点,即AP=PE,且GP=BE,
在△APG和△EGP中,,
∴△APG≌△EPG(SAS),
∴AG=EG=AB,
∴EG=EF,即①正确,
∵EF∥BG,GF∥BE,
∴四边形BGFE为平行四边形,
∴GF=BE,
∵GP=BE=GF,
∴GP=FP,
∵GF⊥AC,
∴∠GPE=∠FPE=90°
在△GPE和△FPE中,,
∴△GPE≌△FPE(SAS),
∴∠GEP=∠FEP,
∴EA平分∠GEF,即④正确.
∵BG=FE,GF=BE,
∴四边形BEFG是平行四边形,
没有条件得出BEFG是菱形,⑤③不正确;
故选:B.
二.填空题(共8小题,满分40分)
9.解:∵四边形ABCD为菱形,
∴AD∥AB,
∴∠BAD=180°﹣∠D=180°﹣110°=70°,
∵四边形ABCD为菱形,
∴AC平分∠BAD,
∴∠BAC=∠BAD=35°.
故答案为:35°.
10.解:∵四边形ABCD是菱形,
∴AD∥BC,AB=AD,∠B=∠D,
在△ABE和△ADF中,
,
∴△ABE≌△ADF(SAS),
∴∠BAE=∠DAF,
∵AD∥BC,
∴∠BAD+∠B=180°,
∵AE=AB,
∴∠B=∠AEB,
设∠B=∠D=∠AEB=x,则∠BAE=∠DAF=180°﹣2x,
∴∠BAD=2(180°﹣2x)+30°,
∴2(180°﹣2x)+30°+x=180°,
解得:x=70°,
即∠D=70°,
故答案为:70°.
11.解:∵四边形ABCD是菱形,
∴AD=AB,BO=OD,∠DAO=∠BAO=25°,AC⊥BD,
∴∠ABD=65°,
∵DH⊥AB,BO=DO,
∴HO=DO,
∴∠DHO=∠BDH=90°﹣∠ABD=25°,
故答案为25°.
12.解:∵四边形ABCD是菱形,AC=8,BD=6,
∴AC⊥OD,OC=AC=4,OD=BD=3,
∴由勾股定理得到:CD==5,
又∵AC BD=CD BE,
∴BE=4.8.
故答案为:4.8.
13.解:如图,连接AC交BD于点G,连接AO,
∵四边形ABCD是菱形,
∴AC⊥BD,AB=AD=10,BG=BD=8,
根据勾股定理得:AG===6,
∵S△ABD=S△AOB+S△AOD,
即BD AG=AB OE+AD OF,
∴16×6=10OE+10OF,
∴OE+OF=9.6.
故答案为:9.6.
14.解:∵菱形ABCD中,AC=6,BD=8,
∴OA=OC=AC=3,OB=BD=4,AC⊥BD,
∴BC===5,
∵OE⊥BC,
∴S△OBC=×OB×OC=×BC×OE,
∴OE===,
故答案为:.
15.解:连接BD交AC于O,
∵四边形ABCD是菱形,
∴AC⊥BD,OA=AC=×6=3,
∵AB=5,
由勾股定理得:OB=4,
∴BD=2OB=8,
∵AB∥CD,
∴△EAB和△ECD的高的和等于点C到直线AB的距离,
∴△EAB和△ECD的面积和=×菱形ABCD的面积=×==12.
故答案为:12
16.解:如图,连接AC,BD,交点为O,EF与AC交于点M,EG与BD交于点N,
∵四边形ABCD是菱形,
∴AC⊥BD,
∵E,F,G分别是AD,AB,CD的中点,
∴EF∥BD,EF=BD,EG∥AC,EG=AC,
∴四边形OMEN是矩形,
∴∠FEG=90°,
∵FG=5cm,EF=3cm,
∴EG===4cm,
∴AC=8cm,BD=6cm,
∴菱形ABCD的面积是AC BD=×8×6=24(cm2).
故答案为24.
三.解答题(共6小题,满分40分)
17.证明:(1)∵四边形AECF是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABD=∠CDB,
∵点E、F为对角线BD的三等分点,
∴BE=EF=DF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS),
∴AE=CF,∠AEB=∠CFD,
∴∠AEF=∠CFE,
∴AE∥CF,
∴四边形AECF是平行四边形;
(2)∵四边形AECF是菱形,
∴AE=AF=CF=CE,
又∵AE=BE,
∴AE=BE=EF=AF=DF,
∴∠EAB=∠EBA,∠EAF=∠EFA,∠FAD=∠FDA,△AEF是等边三角形,
∴∠EAF=∠AFE=∠AEF=60°,
∴∠BAE=30°,∠FAD=30°,
∴∠BAD=120°.
18.(1)证明:∵AE⊥AC,CF⊥AC,
∴AE∥CF,
∵菱形ABCD,
∴AF∥CE,
∴四边形AECF是平行四边形;
(2)解:∵四边形ABCD是菱形,
∴AB=BC,
∴∠BAC=∠BCA
∵AE⊥AC,
∴∠BAC+∠BAE=∠BCA+∠E=90°,
∴∠BAE=∠E,
∴AB=EB,
∵AD=3.5,
∴AB=EB=BC=3.5,
∵AE=6,
∴AE+EC=13,
∵四边形AECF是平行四边形,
∴四边形AECF的周长是26.
19.(1)证明:∵对角线AC的垂直平分线EF分别与AC、BC、AD交于点O、E、F,
∴AF=CF,AE=CE,OA=OC,
∴∠EAC=∠ECA,∠FAC=∠FCA,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EAC=∠FCA,
∴∠FAO=∠ECO,
在△AOF和△COE中,
,
∴△AOF≌△COE(ASA),
∴AF=CE,
∵AF=CF,AE=CE,
∴AE=EC=CF=AF,
∴四边形AECF为菱形;
(2)解:过C作CH⊥AD于H,
则∠CHD=∠CHF=90°,
∵∠D=45°,
∴△CDH是等腰直角三角形,
∴CH=DH=CD,
∵CD=,
∴CH=DH=1,
∵AD=3,
∴AH=2,
∵四边形AECF是菱形,
∴AF=CF,
设AF=CF=x,
则FH=2﹣x,
在Rt△CHF中,由勾股定理得:CF2=FH2+CH2,
∴x2=(2﹣x)2+12,
∴x=,
∴AF=CF=,
∴菱形AECF的周长=×4=5.
20.解:(1)四边形DHBG是菱形,
理由如下:
∵四边形ABCD、四边形FBED是完全相同的矩形,
∴∠A=∠E=90°,AD=ED,AB=EB,
在△DAB和△DEB中,
,
∴△DAB≌△DEB(SAS),
∴∠ABD=∠EBD,
∵AB∥CD,DF∥BE,
∴四边形DHBG是平行四边形,∠HDB=∠EBD,
∴∠HDB=∠HBD,
∴DH=BH,
∴ DHBG是菱形;
(2)∵四边形DHBG的面积为15,
∴BH×AD=15,
∵AD=3,
∴BH=5,
∵四边形DHBG是菱形,
∴DH=BH=5,
由勾股定理得:AH===4,
∴AB=AH+BH=4+5=9.
21.(1)证明:∵四边形ABCD是平行四边形,
∴∠B=∠ADF,
∵AE⊥BC,AF⊥CD,
∴∠AEB=∠AFD=90°,
在△AEB和△AFD中,
,
∴△AEB≌△AFD(ASA),
∴AB=AD,
∴四边形ABCD是菱形;
(2)解:∵∠CEF=30°,AE⊥BC,
∴∠AEF=60°,
由(1)知,△AEB≌△AFD,
∴AE=AF,∠BAE=∠DAF,
∴△AEF是等边三角形,
∴∠EAF=60°,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠AEB=90°,
∴∠DAF=∠DAE﹣∠EAF=30°,
∴∠BAE=30°,
∴BE=AB,
∴AB=2BE,
∵AB2=BE2+AE2,AE=2,
∴(2BE)2=BE2+(2),
∴BE=2,
∴AB=4,
∵由(1)知,四边形ABCD是菱形,
∴四边形ABCD的周长=4AB=16.
22.(1)证明:如图,连接BD,
∵四边形ABCD是菱形,
∴AC⊥DB,AD=AB,
∵EM⊥AC,
∴ME∥BD,
∵点E是AB的中点,
∴点M是AD的中点,AE=AB,
∴AM=AD,
∴AM=AE.
(2)解:①由(1)得,点M是AD的中点,
∴AM=MD,
∵四边形ABCD是菱形,
∴AB∥CD,
∴∠F=∠AEM,∠EAM=∠FDM,
∴△MDF≌△MAE(AAS),
∴AE=DF,
∵AB=2AE,DF=2,
∴AB=4,
∴菱形ABCD的周长为4AB=4×4=16.
②如图,连接CM,记EF与AC交点为点G,
∵AM=AE,△MAE≌△MDF,
∴DF=DM,MF=ME,
∴∠DMF=∠DFM,
∴∠ADC=2∠DFM,
∵∠ADC=2∠MCD,
∴∠MCD=∠DFM,
∴MF=MC=ME,∠EMC=2∠FDM=∠MDC,
∵ME⊥AC,AM=AE,
∴∠MGC=90°,ME=2MG,
∴MC=2MG,
∴∠GMC=60°,
∴∠ADC=60°,
∴∠MCD=30°,
∴∠DMC=90°,
∴△DMC为直角三角形,
∵DF=2,
∴DM=2,CD=4,
∴CM==2,
∴ME=2.
一.选择题(共8小题,满分40分)
1.菱形的对角线长分别是6和8,那么其边长是( )
A.5 B.10 C.20 D.40
2.关于菱形,下列说法错误的是( )
A.对角线互相平分 B.对角线互相垂直
C.四条边相等 D.对角线相等
3.如图,点P,Q分别是菱形ABCD的边AD,BC上的两个动点,若线段PQ长的最大值为8,最小值为8,则菱形ABCD的边长为( )
A.4 B.10 C.12 D.16
4.如图,在菱形ABCD中,M,N分别在AB,CD上,且AM=CN,MN与AC交于点O,连接BO.若∠DAC=26°,则∠OBC的度数为( )
A.54° B.64° C.74° D.26°
5.如图,已知菱形ABCD中,过AD中点E作EF⊥BD,交对角线BD于点M,交BC的延长线于点F.连接DF.若CF=2,则AB的长是( )
A.3 B.4 C.4 D.2
6.如图, ABCD中,AB=5a,BC=4a,∠A=60°,平行四边形内放着两个菱形,菱形DEFG和菱形BHIL,它们的重叠部分是平行四边形IJFK.已知三个阴影平行四边形的周长相等,那么平行四边形IJFK的面积为( )
A.a2 B.2a2 C. D.
7.如图,阴影部分是一个菱形剪去一个平行四边形后所剩下的,要想知道阴影部分的周长,需要测量线段( )的长度.
A.AB与BC B.AB与DE C.AF D.AB
8.如图,平行四边形ABCD中,对角线AC,BD交于点O,BD=2AD,E,F,G分别是OC,OD,AB的中点.下列结论正确的是( )
①EG=EF;②△EFG≌△GBE;③FB平分∠EFG;④EA平分∠GEF;
⑤四边形BEFG是菱形.
A.③⑤ B.①②④ C.①②③④ D.①②③④⑤
二.填空题(共8小题,满分40分)
9.如图,菱形ABCD中,已知∠D=110°,则∠BAC的度数为 .
10.如图,在菱形ABCD中,E,F分别在BC,DC上,BE=DF,AE=AB,若∠EAF=30°,则∠D的度数是 .
11.如图,四边形ABCD为菱形,对角线AC,BD相交于点O,DH⊥AB于点H,连接OH,∠CAD=25°,则∠DHO的度数是 .
12.如图,菱形ABCD中,对角线AC=8,BD=6,BE⊥CD,则BE= .
13.如图,在边长为10的菱形ABCD中,对角线BD=16,点O是线段BD上的动点,OE⊥AB于E,OF⊥AD于F.则OE+OF= .
14.如图,菱形ABCD的对角线AC,BD相交于点O,过点O作OE⊥BC于点E,若AC=6,BD=8,则OE= .
15.如图,在菱形ABCD中,AC=6,AB=5,点E是直线AB、CD之间任意一点,连接AE、BE、DE、CE,则△EAB和△ECD的面积和等于 .
16.如图,在菱形ABCD中,E,F,G分别是AD,AB,CD的中点,且FG=5cm,EF=3cm,则菱形ABCD的面积是 cm2.
三.解答题(共6小题,满分40分)
17.如图,在 ABCD中,点E、F为对角线BD的三等分点,连接AE,CF,AF,CE.
(1)求证:四边形AECF为平行四边形;
(2)若四边形AECF为菱形,且AE=BE,求∠BAD的度数.
18.如图,线段AC是菱形ABCD的一条对角线,过顶点A、C分别作对角线AC的垂线,交CB、AD的延长线于点E、F.
(1)求证:四边形AECF是平行四边形;
(2)若AD=3.5,AE=6,求证四边形AECF的周长.
19.如图,在平行四边形ABCD中,EF垂直平分对角线AC,分别与边AD,BC交于点F,E.
(1)求证:四边形AECF为菱形;
(2)若AD=3,CD=,且∠D=45°,求菱形AECF的周长.
20.将两张完全相同的矩形纸片ABCD,矩形纸片FBED按如图方式放置,BD为重合的对角线.重叠部分为四边形DHBG.
(1)试判断四边形DHBG为何种特殊的四边形,并说明理由;
(2)若四边形DHBG的面积为15,AD=3,求AB的长.
21.如图,四边形ABCD是平行四边形,AE⊥BC于E,AF⊥CD于F,且BE=DF.
(1)求证:四边形ABCD是菱形.
(2)连接EF,若∠CEF=30°,AE=,直接写出四边形ABCD的周长.
22.如图,四边形ABCD是菱形,E是AB的中点,AC的垂线EF交AD于点M,交CD的延长线于点F.
(1)求证:AM=AE;
(2)连接CM,DF=2.
①求菱形ABCD的周长;
②若∠ADC=2∠MCF,求ME的长.
参考答案
一.选择题(共8小题,满分40分)
1.解:如图,菱形ABCD中,BD=8,AC=6,
则AC⊥BD,OB=4,OA=3,
∴AB=,
故选:A.
2.解:∵菱形的性质有四边相等,对角线互相垂直平分,
∴对角线相等不是菱形的性质,
故选:D.
3.解:如图,过点C作CH⊥AB,交AB的延长线于H,
∵四边形ABCD是菱形,
∴AD=AB=BC,
∵点P,Q分别是菱形ABCD的边AD,BC上的两个动点,
∴当点P与点A重合,点Q与点C重合时,PQ有最大值,即AC=8,
当PQ⊥BC时,PQ有最小值,即直线CD,直线AB的距离为8,即CH=8,
∴AH===16,
∵BC2=CH2+BH2,
∴BC2=(16﹣BC)2+64,
∴BC=10,
故选:B.
4.解:∵四边形ABCD为菱形,
∴AB∥CD,AB=BC,
∴∠MAO=∠NCO,∠AMO=∠CNO,
在△AMO和△CNO中,
,
∴△AMO≌△CNO(ASA),
∴AO=CO,
∵AB=BC,
∴BO⊥AC,
∴∠BOC=90°,
∵∠DAC=26°,
∴∠BCA=∠DAC=26°,
∴∠OBC=90°﹣26°=64°.
故选:B.
5.解:设CD与EF的交点为H,
∵四边形ABCD是菱形,
∴AD=CD=BC,∠ADB=∠CDB,
∵点E是AD中点,
∴AE=DE=AD,
在△DEM和△DHM中,
,
∴△DEM≌△DHM(ASA),
∴DE=DH,
∴DH=CH,
∵AD∥BC,
∴DE=CF=2,
∴AD=4=CD=BC=AB.
故选:C.
6.解:由题意 ABCD的周长为2(AB+BC)=18a,
又∵三个阴影平行四边形的周长相等,
∴由平移的性质可得: EALJ的周长= IJFK的周长= GKHC的周长=×18a=6a,
∴IJ+JF=EJ+JL=GK+KH=3a,
∴HI=IK+KH=3a,DG=EJ+JF=3a,
∴DG=HI,
∴IJ+JL+JF+EJ=6a,IJ+KH+GK+JF=6a,
又∵AB=5a,BC=4a,且四边形DEFG和四边形BHIL是菱形,
∴EF=IL=3a,AE=JF=a,IJ=2a,∠IJF=∠DEF=∠A=60°,
过点I作IP⊥EF,
∴在Rt△IJP中,
JP=IJ=a,IP==a,
∴平行四边形IJFK的面积为JF IP=a2,
故选:D.
7.解:如图,延长AB,ED交于点H,
∵四边形BCDH是平行四边形,
∴BC=DH,CD=BH,
∵四边形AFEH是菱形,
∴AF=EF=EH=AH,
∴阴影部分的周长=AB+BC+CD+DE+EF+EF=4AF,
故需要测量AF的长度,
故选:C.
8.解:设GF和AC的交点为点P,如图:
∵E、F分别是OC、OD的中点,
∴EF∥CD,且EF=CD,
∵四边形ABCD为平行四边形,
∴AB∥CD,且AB=CD,
∴∠FEG=∠BGE,
∵点G为AB的中点,
∴BG=AB=CD=FE,
在△EFG和△GBE中,,
∴△EFG≌△GBE(SAS),即②正确,
∴∠EGF=∠GEB,GF=BE,
∴GF∥BE,
∵BD=2BC,点O为平行四边形对角线交点,
∴BO=BD=BC,
∵E为OC中点,
∴BE⊥OC,
∴GP⊥AC,
∴∠APG=∠EPG=90°
∵GP∥BE,G为AB中点,
∴P为AE中点,即AP=PE,且GP=BE,
在△APG和△EGP中,,
∴△APG≌△EPG(SAS),
∴AG=EG=AB,
∴EG=EF,即①正确,
∵EF∥BG,GF∥BE,
∴四边形BGFE为平行四边形,
∴GF=BE,
∵GP=BE=GF,
∴GP=FP,
∵GF⊥AC,
∴∠GPE=∠FPE=90°
在△GPE和△FPE中,,
∴△GPE≌△FPE(SAS),
∴∠GEP=∠FEP,
∴EA平分∠GEF,即④正确.
∵BG=FE,GF=BE,
∴四边形BEFG是平行四边形,
没有条件得出BEFG是菱形,⑤③不正确;
故选:B.
二.填空题(共8小题,满分40分)
9.解:∵四边形ABCD为菱形,
∴AD∥AB,
∴∠BAD=180°﹣∠D=180°﹣110°=70°,
∵四边形ABCD为菱形,
∴AC平分∠BAD,
∴∠BAC=∠BAD=35°.
故答案为:35°.
10.解:∵四边形ABCD是菱形,
∴AD∥BC,AB=AD,∠B=∠D,
在△ABE和△ADF中,
,
∴△ABE≌△ADF(SAS),
∴∠BAE=∠DAF,
∵AD∥BC,
∴∠BAD+∠B=180°,
∵AE=AB,
∴∠B=∠AEB,
设∠B=∠D=∠AEB=x,则∠BAE=∠DAF=180°﹣2x,
∴∠BAD=2(180°﹣2x)+30°,
∴2(180°﹣2x)+30°+x=180°,
解得:x=70°,
即∠D=70°,
故答案为:70°.
11.解:∵四边形ABCD是菱形,
∴AD=AB,BO=OD,∠DAO=∠BAO=25°,AC⊥BD,
∴∠ABD=65°,
∵DH⊥AB,BO=DO,
∴HO=DO,
∴∠DHO=∠BDH=90°﹣∠ABD=25°,
故答案为25°.
12.解:∵四边形ABCD是菱形,AC=8,BD=6,
∴AC⊥OD,OC=AC=4,OD=BD=3,
∴由勾股定理得到:CD==5,
又∵AC BD=CD BE,
∴BE=4.8.
故答案为:4.8.
13.解:如图,连接AC交BD于点G,连接AO,
∵四边形ABCD是菱形,
∴AC⊥BD,AB=AD=10,BG=BD=8,
根据勾股定理得:AG===6,
∵S△ABD=S△AOB+S△AOD,
即BD AG=AB OE+AD OF,
∴16×6=10OE+10OF,
∴OE+OF=9.6.
故答案为:9.6.
14.解:∵菱形ABCD中,AC=6,BD=8,
∴OA=OC=AC=3,OB=BD=4,AC⊥BD,
∴BC===5,
∵OE⊥BC,
∴S△OBC=×OB×OC=×BC×OE,
∴OE===,
故答案为:.
15.解:连接BD交AC于O,
∵四边形ABCD是菱形,
∴AC⊥BD,OA=AC=×6=3,
∵AB=5,
由勾股定理得:OB=4,
∴BD=2OB=8,
∵AB∥CD,
∴△EAB和△ECD的高的和等于点C到直线AB的距离,
∴△EAB和△ECD的面积和=×菱形ABCD的面积=×==12.
故答案为:12
16.解:如图,连接AC,BD,交点为O,EF与AC交于点M,EG与BD交于点N,
∵四边形ABCD是菱形,
∴AC⊥BD,
∵E,F,G分别是AD,AB,CD的中点,
∴EF∥BD,EF=BD,EG∥AC,EG=AC,
∴四边形OMEN是矩形,
∴∠FEG=90°,
∵FG=5cm,EF=3cm,
∴EG===4cm,
∴AC=8cm,BD=6cm,
∴菱形ABCD的面积是AC BD=×8×6=24(cm2).
故答案为24.
三.解答题(共6小题,满分40分)
17.证明:(1)∵四边形AECF是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABD=∠CDB,
∵点E、F为对角线BD的三等分点,
∴BE=EF=DF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS),
∴AE=CF,∠AEB=∠CFD,
∴∠AEF=∠CFE,
∴AE∥CF,
∴四边形AECF是平行四边形;
(2)∵四边形AECF是菱形,
∴AE=AF=CF=CE,
又∵AE=BE,
∴AE=BE=EF=AF=DF,
∴∠EAB=∠EBA,∠EAF=∠EFA,∠FAD=∠FDA,△AEF是等边三角形,
∴∠EAF=∠AFE=∠AEF=60°,
∴∠BAE=30°,∠FAD=30°,
∴∠BAD=120°.
18.(1)证明:∵AE⊥AC,CF⊥AC,
∴AE∥CF,
∵菱形ABCD,
∴AF∥CE,
∴四边形AECF是平行四边形;
(2)解:∵四边形ABCD是菱形,
∴AB=BC,
∴∠BAC=∠BCA
∵AE⊥AC,
∴∠BAC+∠BAE=∠BCA+∠E=90°,
∴∠BAE=∠E,
∴AB=EB,
∵AD=3.5,
∴AB=EB=BC=3.5,
∵AE=6,
∴AE+EC=13,
∵四边形AECF是平行四边形,
∴四边形AECF的周长是26.
19.(1)证明:∵对角线AC的垂直平分线EF分别与AC、BC、AD交于点O、E、F,
∴AF=CF,AE=CE,OA=OC,
∴∠EAC=∠ECA,∠FAC=∠FCA,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EAC=∠FCA,
∴∠FAO=∠ECO,
在△AOF和△COE中,
,
∴△AOF≌△COE(ASA),
∴AF=CE,
∵AF=CF,AE=CE,
∴AE=EC=CF=AF,
∴四边形AECF为菱形;
(2)解:过C作CH⊥AD于H,
则∠CHD=∠CHF=90°,
∵∠D=45°,
∴△CDH是等腰直角三角形,
∴CH=DH=CD,
∵CD=,
∴CH=DH=1,
∵AD=3,
∴AH=2,
∵四边形AECF是菱形,
∴AF=CF,
设AF=CF=x,
则FH=2﹣x,
在Rt△CHF中,由勾股定理得:CF2=FH2+CH2,
∴x2=(2﹣x)2+12,
∴x=,
∴AF=CF=,
∴菱形AECF的周长=×4=5.
20.解:(1)四边形DHBG是菱形,
理由如下:
∵四边形ABCD、四边形FBED是完全相同的矩形,
∴∠A=∠E=90°,AD=ED,AB=EB,
在△DAB和△DEB中,
,
∴△DAB≌△DEB(SAS),
∴∠ABD=∠EBD,
∵AB∥CD,DF∥BE,
∴四边形DHBG是平行四边形,∠HDB=∠EBD,
∴∠HDB=∠HBD,
∴DH=BH,
∴ DHBG是菱形;
(2)∵四边形DHBG的面积为15,
∴BH×AD=15,
∵AD=3,
∴BH=5,
∵四边形DHBG是菱形,
∴DH=BH=5,
由勾股定理得:AH===4,
∴AB=AH+BH=4+5=9.
21.(1)证明:∵四边形ABCD是平行四边形,
∴∠B=∠ADF,
∵AE⊥BC,AF⊥CD,
∴∠AEB=∠AFD=90°,
在△AEB和△AFD中,
,
∴△AEB≌△AFD(ASA),
∴AB=AD,
∴四边形ABCD是菱形;
(2)解:∵∠CEF=30°,AE⊥BC,
∴∠AEF=60°,
由(1)知,△AEB≌△AFD,
∴AE=AF,∠BAE=∠DAF,
∴△AEF是等边三角形,
∴∠EAF=60°,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠AEB=90°,
∴∠DAF=∠DAE﹣∠EAF=30°,
∴∠BAE=30°,
∴BE=AB,
∴AB=2BE,
∵AB2=BE2+AE2,AE=2,
∴(2BE)2=BE2+(2),
∴BE=2,
∴AB=4,
∵由(1)知,四边形ABCD是菱形,
∴四边形ABCD的周长=4AB=16.
22.(1)证明:如图,连接BD,
∵四边形ABCD是菱形,
∴AC⊥DB,AD=AB,
∵EM⊥AC,
∴ME∥BD,
∵点E是AB的中点,
∴点M是AD的中点,AE=AB,
∴AM=AD,
∴AM=AE.
(2)解:①由(1)得,点M是AD的中点,
∴AM=MD,
∵四边形ABCD是菱形,
∴AB∥CD,
∴∠F=∠AEM,∠EAM=∠FDM,
∴△MDF≌△MAE(AAS),
∴AE=DF,
∵AB=2AE,DF=2,
∴AB=4,
∴菱形ABCD的周长为4AB=4×4=16.
②如图,连接CM,记EF与AC交点为点G,
∵AM=AE,△MAE≌△MDF,
∴DF=DM,MF=ME,
∴∠DMF=∠DFM,
∴∠ADC=2∠DFM,
∵∠ADC=2∠MCD,
∴∠MCD=∠DFM,
∴MF=MC=ME,∠EMC=2∠FDM=∠MDC,
∵ME⊥AC,AM=AE,
∴∠MGC=90°,ME=2MG,
∴MC=2MG,
∴∠GMC=60°,
∴∠ADC=60°,
∴∠MCD=30°,
∴∠DMC=90°,
∴△DMC为直角三角形,
∵DF=2,
∴DM=2,CD=4,
∴CM==2,
∴ME=2.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
