2021--2022学年人教版九年级下册数学27.2.1相似三角形的判定同步习题(Word版含答案)
文档属性
| 名称 | 2021--2022学年人教版九年级下册数学27.2.1相似三角形的判定同步习题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 250.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-19 21:12:22 | ||
图片预览


文档简介
27.2.1相似三角形的判定 同步习题
一.选择题
1.下列图形一定是相似图形的是( )
A.两个钝角三角形 B.两个直角三角形
C.两个等腰三角形 D.两个等腰直角三角形
2.在Rt△ABC中,∠ACB=90°,CD是△ABC的高,E是AC的中点,ED、CB的延长线相交于点F,则图中相似三角形有( )
A. 3对
B. 4对
C. 5对
D. 6对
3.下列4组条件中,能判定△ABC∽△DEF的是( )
A.AB=5,BC=4,∠A=45°;DE=10,EF=8,∠D=45°
B. ∠A=45°,∠B=55°;∠D=45°,∠F=75°
C.BC=4,AC=6,AB=9;DE=18,EF=8,DF=12
D.AB=6,BC=5,∠B=40°;DE=5,EF=4,∠E=40°
4.如图,在△ABC中,∠A=78°,AB=4,AC=6,将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
A.
B.
C.
D.
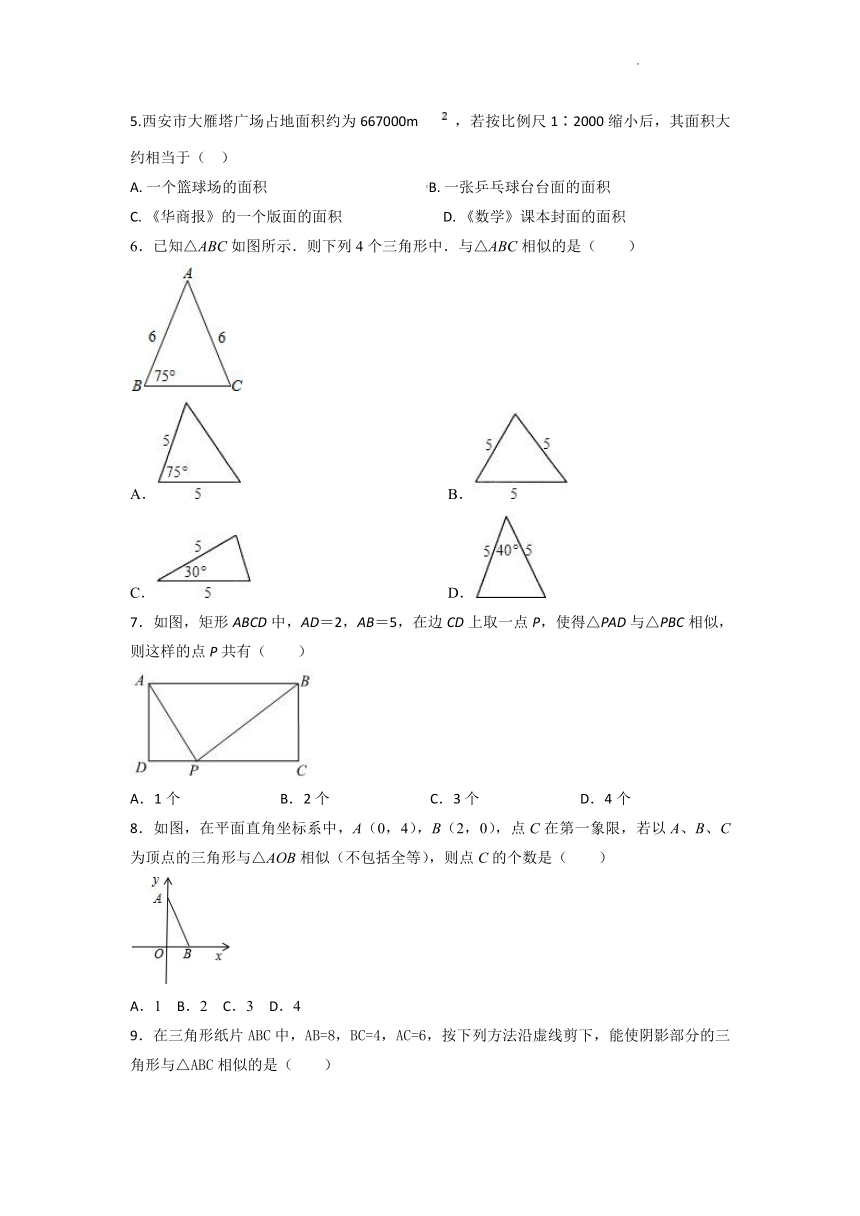
5.西安市大雁塔广场占地面积约为667000m ,若按比例尺1∶2000缩小后,其面积大约相当于( )
A. 一个篮球场的面积 B. 一张乒乓球台台面的面积
C. 《华商报》的一个版面的面积 D. 《数学》课本封面的面积
6.已知△ABC如图所示.则下列4个三角形中.与△ABC相似的是( )
A. B.
C. D.
7.如图,矩形ABCD中,AD=2,AB=5,在边CD上取一点P,使得△PAD与△PBC相似,则这样的点P共有( )
A.1个 B.2个 C.3个 D.4个
8.如图,在平面直角坐标系中,A(0,4),B(2,0),点C在第一象限,若以A、B、C为顶点的三角形与△AOB相似(不包括全等),则点C的个数是( )
A.1 B.2 C.3 D.4
9.在三角形纸片ABC中,AB=8,BC=4,AC=6,按下列方法沿虚线剪下,能使阴影部分的三角形与△ABC相似的是( )
10.如图,在正方形ABCD中,E是AD的中点,F是CD上一点,且CF=3FD.则图中相似三角形的对数是( )
A.1 B. 2 C.3 D.)4
二.填空题
11.如图,一次函数y=﹣x+6的图象与x轴交于点B,与y轴交于点A,过线段AB的中点P(4,3)作一条直线与△AOB交于点Q,使得所截新三角形与△AOB相似,则点Q坐标是 .
12.△ADE中,AD=AE,C为DE延长线上一点,B为ED延长线上一点,∠DAE=40°,当∠BAC=____________时,△BDA∽△AEC.
13.如图,△ABC与△FAG是两个全等的等腰直角三角形,∠BAC=∠F=90°,BC分别与AF、AG相交于点D、E.则图中不全等的相似三角形有____________对.
14.如图,平面直角坐标系中,已知点A(4,0)和点B(0,3),点C是AB的中点,点P在折线AOB上,直线CP截△AOB,所得的三角形与△AOB相似,那么点P的坐标是____________________.
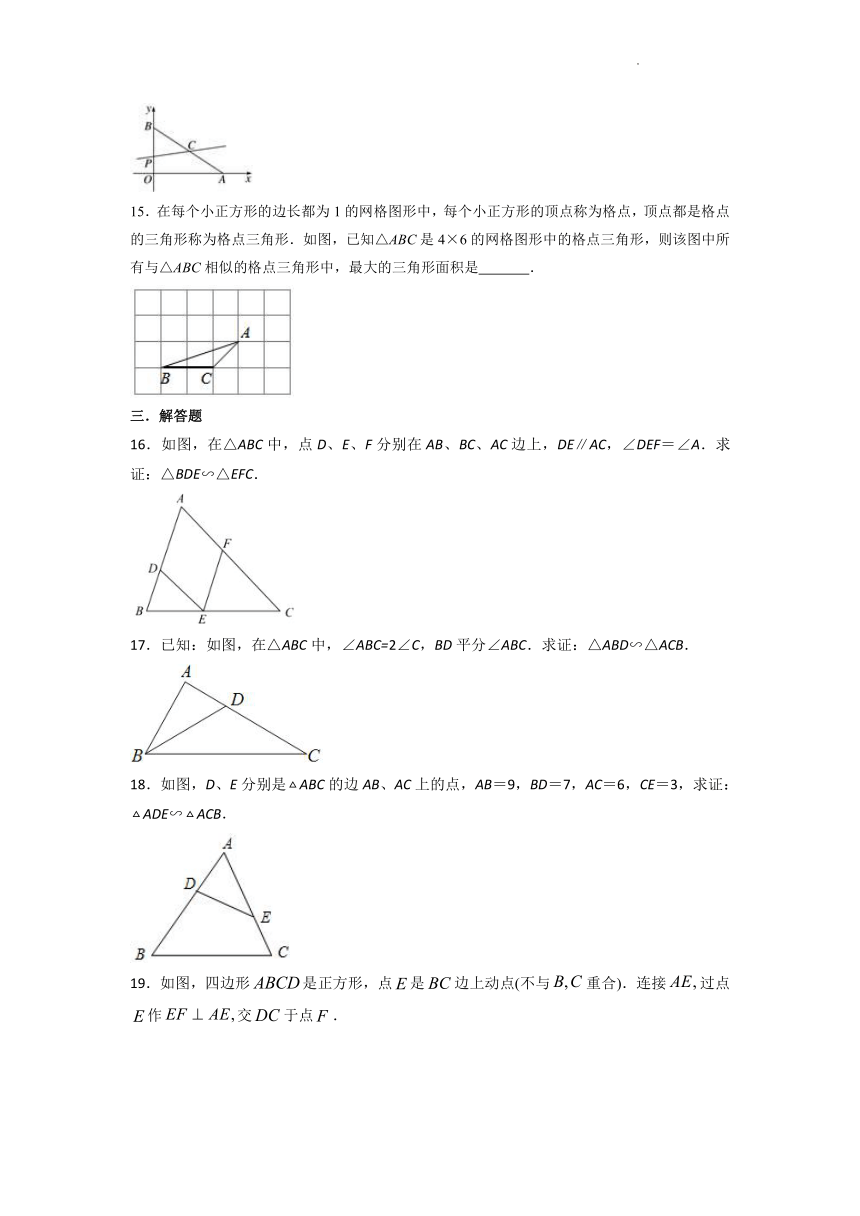
15.在每个小正方形的边长都为1的网格图形中,每个小正方形的顶点称为格点,顶点都是格点的三角形称为格点三角形.如图,已知△ABC是4×6的网格图形中的格点三角形,则该图中所有与△ABC相似的格点三角形中,最大的三角形面积是 .
三.解答题
16.如图,在△ABC中,点D、E、F分别在AB、BC、AC边上,DE∥AC,∠DEF=∠A.求证:△BDE∽△EFC.
17.已知:如图,在△ABC中,∠ABC=2∠C,BD平分∠ABC.求证:△ABD∽△ACB.
18.如图,D、E分别是ABC的边AB、AC上的点,AB=9,BD=7,AC=6,CE=3,求证:ADE∽ACB.
19.如图,四边形是正方形,点是边上动点(不与重合).连接过点作交于点.
求证:;
连接,试探究当点在什么位置时,,请证明你的结论.
20.如图,已知P是菱形ABCD中CD边上一点,AP交对角线BD于点E,将沿AP翻折得,FP交边BC于点G,.
(1)求证:;
(2)若,,求的长.
1.A 2.B 3.C 4.D 5.B 6.C 7.C 8.D 9.D 10.C
11.(0,3)或(,0)或(4,0).
12.【答案】110°
13.【答案】3
14.【答案】(0,),(2,0),(,0)
15.4.
16.证明,
,
又,
,
,
,
.
17.证明:∵BD平分∠ABC,
∴∠ABC=2∠ABD
∵∠ABC=2∠C
∴∠ABD=∠C
∵∠A=∠A
∴△ABD∽△ACB.
18.证明:∵AB=9,BD=7,AC=6,CE=3,
∴AD=AB﹣BD=9﹣7=2,AE=AC﹣CE=6﹣3=3,
∵,,
∴,
又∠A=∠A,
∴△ADE∽△ACB.
19.(1)
在中,
又
;
(2),
是等腰直角三角形
BC=6,
AB=AC=BC=3
①当AD=AE时,则
,
点D在上运动时(点D不与重合),点E在AC上
此情况不符合题意.
②当AD=DE时,如图,
由(1)可知
又
:
AB=DC=
.
③当AE=DE时,如图
,
平分,
.
综上所述:或.
20.(1)∵,
∴,,,
即.
(2)由(1)知,,
又∵
∴,,,
∴∽(对应边成比例,对应角分别相等的两个三角形相似).
一.选择题
1.下列图形一定是相似图形的是( )
A.两个钝角三角形 B.两个直角三角形
C.两个等腰三角形 D.两个等腰直角三角形
2.在Rt△ABC中,∠ACB=90°,CD是△ABC的高,E是AC的中点,ED、CB的延长线相交于点F,则图中相似三角形有( )
A. 3对
B. 4对
C. 5对
D. 6对
3.下列4组条件中,能判定△ABC∽△DEF的是( )
A.AB=5,BC=4,∠A=45°;DE=10,EF=8,∠D=45°
B. ∠A=45°,∠B=55°;∠D=45°,∠F=75°
C.BC=4,AC=6,AB=9;DE=18,EF=8,DF=12
D.AB=6,BC=5,∠B=40°;DE=5,EF=4,∠E=40°
4.如图,在△ABC中,∠A=78°,AB=4,AC=6,将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
A.
B.
C.
D.
5.西安市大雁塔广场占地面积约为667000m ,若按比例尺1∶2000缩小后,其面积大约相当于( )
A. 一个篮球场的面积 B. 一张乒乓球台台面的面积
C. 《华商报》的一个版面的面积 D. 《数学》课本封面的面积
6.已知△ABC如图所示.则下列4个三角形中.与△ABC相似的是( )
A. B.
C. D.
7.如图,矩形ABCD中,AD=2,AB=5,在边CD上取一点P,使得△PAD与△PBC相似,则这样的点P共有( )
A.1个 B.2个 C.3个 D.4个
8.如图,在平面直角坐标系中,A(0,4),B(2,0),点C在第一象限,若以A、B、C为顶点的三角形与△AOB相似(不包括全等),则点C的个数是( )
A.1 B.2 C.3 D.4
9.在三角形纸片ABC中,AB=8,BC=4,AC=6,按下列方法沿虚线剪下,能使阴影部分的三角形与△ABC相似的是( )
10.如图,在正方形ABCD中,E是AD的中点,F是CD上一点,且CF=3FD.则图中相似三角形的对数是( )
A.1 B. 2 C.3 D.)4
二.填空题
11.如图,一次函数y=﹣x+6的图象与x轴交于点B,与y轴交于点A,过线段AB的中点P(4,3)作一条直线与△AOB交于点Q,使得所截新三角形与△AOB相似,则点Q坐标是 .
12.△ADE中,AD=AE,C为DE延长线上一点,B为ED延长线上一点,∠DAE=40°,当∠BAC=____________时,△BDA∽△AEC.
13.如图,△ABC与△FAG是两个全等的等腰直角三角形,∠BAC=∠F=90°,BC分别与AF、AG相交于点D、E.则图中不全等的相似三角形有____________对.
14.如图,平面直角坐标系中,已知点A(4,0)和点B(0,3),点C是AB的中点,点P在折线AOB上,直线CP截△AOB,所得的三角形与△AOB相似,那么点P的坐标是____________________.
15.在每个小正方形的边长都为1的网格图形中,每个小正方形的顶点称为格点,顶点都是格点的三角形称为格点三角形.如图,已知△ABC是4×6的网格图形中的格点三角形,则该图中所有与△ABC相似的格点三角形中,最大的三角形面积是 .
三.解答题
16.如图,在△ABC中,点D、E、F分别在AB、BC、AC边上,DE∥AC,∠DEF=∠A.求证:△BDE∽△EFC.
17.已知:如图,在△ABC中,∠ABC=2∠C,BD平分∠ABC.求证:△ABD∽△ACB.
18.如图,D、E分别是ABC的边AB、AC上的点,AB=9,BD=7,AC=6,CE=3,求证:ADE∽ACB.
19.如图,四边形是正方形,点是边上动点(不与重合).连接过点作交于点.
求证:;
连接,试探究当点在什么位置时,,请证明你的结论.
20.如图,已知P是菱形ABCD中CD边上一点,AP交对角线BD于点E,将沿AP翻折得,FP交边BC于点G,.
(1)求证:;
(2)若,,求的长.
1.A 2.B 3.C 4.D 5.B 6.C 7.C 8.D 9.D 10.C
11.(0,3)或(,0)或(4,0).
12.【答案】110°
13.【答案】3
14.【答案】(0,),(2,0),(,0)
15.4.
16.证明,
,
又,
,
,
,
.
17.证明:∵BD平分∠ABC,
∴∠ABC=2∠ABD
∵∠ABC=2∠C
∴∠ABD=∠C
∵∠A=∠A
∴△ABD∽△ACB.
18.证明:∵AB=9,BD=7,AC=6,CE=3,
∴AD=AB﹣BD=9﹣7=2,AE=AC﹣CE=6﹣3=3,
∵,,
∴,
又∠A=∠A,
∴△ADE∽△ACB.
19.(1)
在中,
又
;
(2),
是等腰直角三角形
BC=6,
AB=AC=BC=3
①当AD=AE时,则
,
点D在上运动时(点D不与重合),点E在AC上
此情况不符合题意.
②当AD=DE时,如图,
由(1)可知
又
:
AB=DC=
.
③当AE=DE时,如图
,
平分,
.
综上所述:或.
20.(1)∵,
∴,,,
即.
(2)由(1)知,,
又∵
∴,,,
∴∽(对应边成比例,对应角分别相等的两个三角形相似).
