2021—2022学年人教版九年级数学下册27.2相似三角形性质与判定同步练习卷(Word版含答案)
文档属性
| 名称 | 2021—2022学年人教版九年级数学下册27.2相似三角形性质与判定同步练习卷(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 526.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-19 21:13:47 | ||
图片预览



文档简介
相似三角形性质与判定
一、选择题
1.两个相似三角形的最短边分别为5 cm和3 cm,他们的周长之差为12 cm,那么大三角形的周长为( )
A.14 cm B.16 cm C.18 cm D.30 cm
2.如图,在△ABC,AB=AC=a,点D是边BC上的一点,且BD=a,AD=DC=1,则a等于( )
A. B. C.1 D.2
3.如图,在 ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则△DEF与四边形EFCO的面积比为( )
A.1:4 B.1:5 C.1:6 D.1:7
4.如图,在正方形ABCD中,点E为边AD上的一个动点(与点A、D不重合),∠EBM=45°,BE交对角线AC于点F,BM交对角线AC于点G,交边CD于点M,那么下列结论中,错误的是( )
A.△AEF∽△CBF B.△CMG∽△BFG C.△ABG∽△CFB D.△ABF∽△CBG
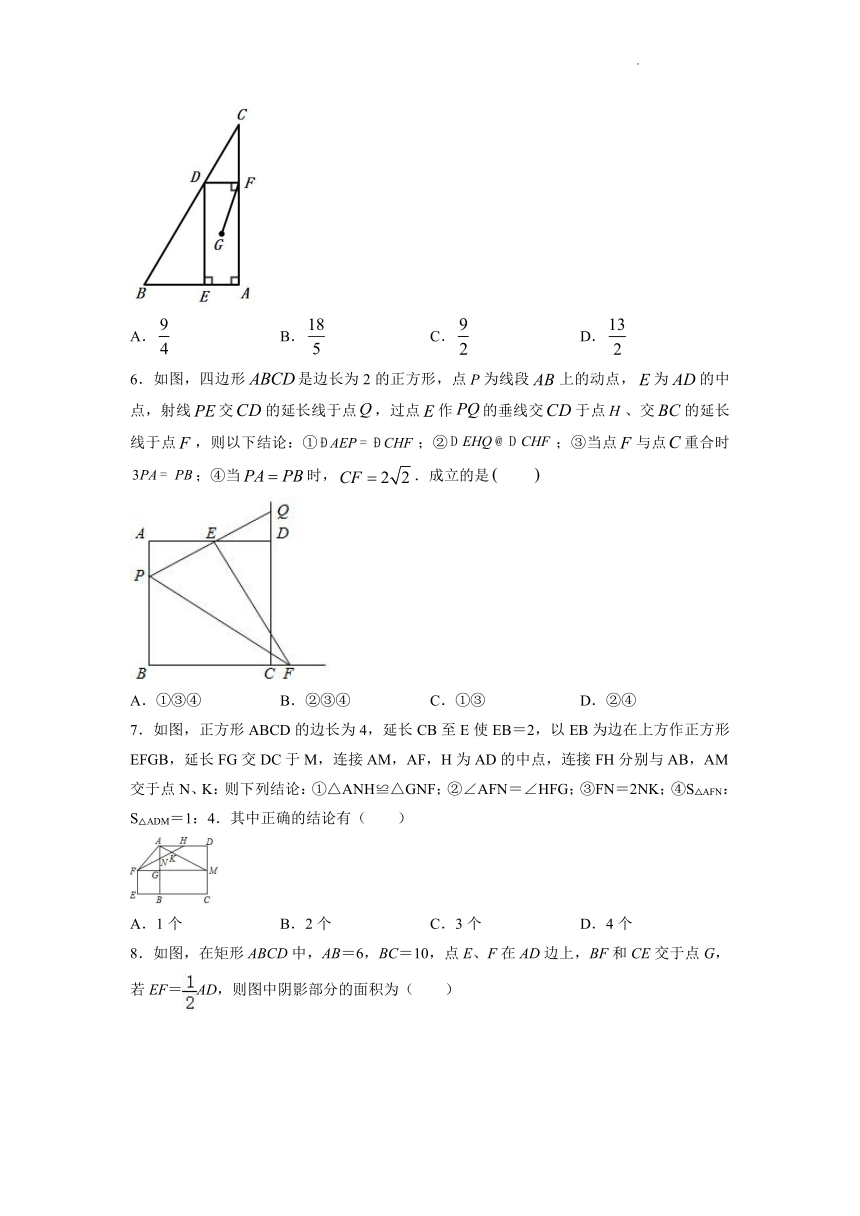
5.如图,中,BA=9,AC=12,点D是斜边BC上一动点,过点D分别作于点E,于点F,点G为四边形DEAF对角线交点,则线段GF的最小值为( ).
A. B. C. D.
6.如图,四边形是边长为2的正方形,点为线段上的动点,为的中点,射线交的延长线于点,过点作的垂线交于点、交的延长线于点,则以下结论:①;②;③当点与点重合时;④当时,.成立的是
A.①③④ B.②③④ C.①③ D.②④
7.如图,正方形ABCD的边长为4,延长CB至E使EB=2,以EB为边在上方作正方形EFGB,延长FG交DC于M,连接AM,AF,H为AD的中点,连接FH分别与AB,AM交于点N、K:则下列结论:①△ANH≌△GNF;②∠AFN=∠HFG;③FN=2NK;④S△AFN:S△ADM=1:4.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
8.如图,在矩形ABCD中,AB=6,BC=10,点E、F在AD边上,BF和CE交于点G,若EF=AD,则图中阴影部分的面积为( )
A.25 B.30 C.35 D.40
9.如图,△ABC是等边三角形,点D,E,F分别在AB,BC,AC边上,且AD=BE=CF,若DE⊥BC,则△DEF与△ABC的面积比为( )
A. B. C. D.
10.如图,在△ABC中,点E、F在边BC上,点E、B不重合.BE=CF,点D在边AC上,连接ED、DF,∠A=∠EDF=120°,若=m,,则m的值为( )
A. B. C. D.
二、填空题
11.如果一个三角形的三边长为5、12、13,与其相似的三角形的最长的边为39,那么较大的三角形的周长为 ,面积为 .
12.如图,已如AB=AC=DE,D为BC延长线上一点,过D作DE⊥BC于E交AC于F,若AB=m,AF=n,则AE+EF (用含m,n的式子表示).
13.如图,四边形ABCD中,AC平分∠BAD,CD⊥AD,点E为AB的中点,DE交AC于点F.若AB=,AC=,BC=1,则AF的长为 .
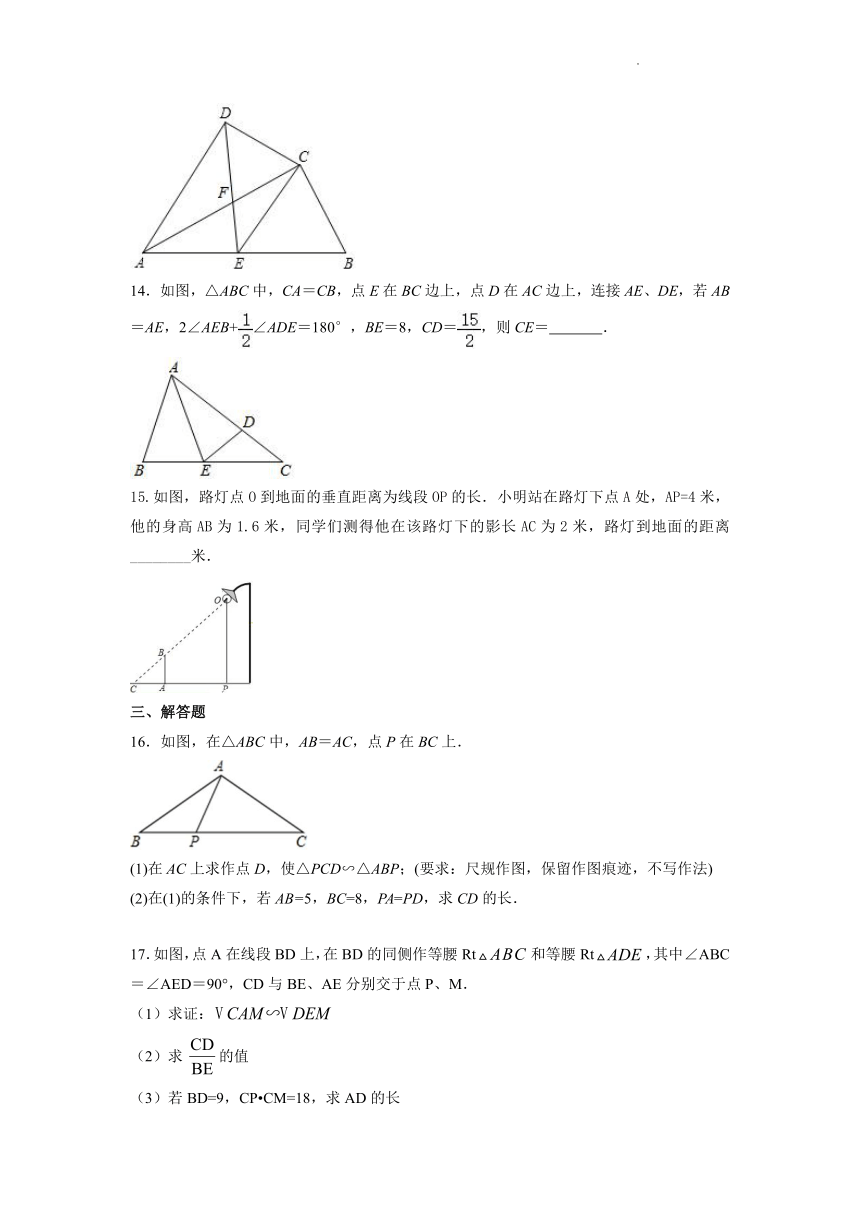
14.如图,△ABC中,CA=CB,点E在BC边上,点D在AC边上,连接AE、DE,若AB=AE,2∠AEB+∠ADE=180°,BE=8,CD=,则CE= .
15.如图,路灯点O到地面的垂直距离为线段OP的长.小明站在路灯下点A处,AP=4米,他的身高AB为1.6米,同学们测得他在该路灯下的影长AC为2米,路灯到地面的距离________米.
三、解答题
16.如图,在△ABC中,AB=AC,点P在BC上.
(1)在AC上求作点D,使△PCD∽△ABP;(要求:尺规作图,保留作图痕迹,不写作法)
(2)在(1)的条件下,若AB=5,BC=8,PA=PD,求CD的长.
17.如图,点A在线段BD上,在BD的同侧作等腰Rt和等腰Rt,其中∠ABC=∠AED=90°,CD与BE、AE分别交于点P、M.
(1)求证:
(2)求的值
(3)若BD=9,CP CM=18,求AD的长
18.如图①,中,,.动点以的速度由出发沿线段向运动,动点以的速度由出发沿射线运动.当点运动时,点开始运动;点到达终点时,、一起停止.设点运动的时间为,的面积为,与的函数关系图像如图②所示.
(1)点运动的速度______,______;
(2)当为何值时,的面积为;
(3)是否存在,使得直线将的周长与面积同时平分?若存在,求出的值;若不存在,请说明理由.
19.如图,已知∠DAB=∠EAC,∠ADE=∠ABC.求证:
(1)△ADE∽△ABC;
(2)=.
20.如图,在△ABC中,AD、BE是中线,它们相交于点F,EG//BC,交AD于点G.
(1)求证:△FGE∽△FDB;
(2)求AG:DF的值.
21.小明利用灯光下自己的影子长度来测量路灯的高度.如图,CD和EF是两等高的路灯,相距27m,身高1.5m的小明(AB)站在两路灯之间(D.B.F共线),被两路灯同时照射留在地面的影长BQ=4m,BP=5m.
(1)小明距离路灯多远?
(2)求路灯高度.
参考答案
1.D 2.A 3.B 4.D 5.B 6.C 7.C 8.C 9.C 10.B
11.答案为:较大三角形的周长为90,面积为270.
12.=2m﹣n.
13..
14.12.
15.答案为:10.
16.解:(1)∵AB=AC
∴∠C=∠B,
∵△PCD∽△ABP,
∴∠CPD=∠BAP,
故作∠CPD=∠BAP即可,
如图,即为所作图形,
(2)∵△PCD∽△ABP
∴
∵PA=PD
∴PC=AB=5
∴CD=BP=8-5=3
17.解:(1)证明:∵ΔABC与ΔADE均为等腰直角三角形
∴∠BAC=∠EAD=45°
∴∠CAE=90°=∠AED
∴AC∥DE
∴ △CAM∽△DEM
(2)∵ΔABC与ΔADE均为等腰直角三角形
∴,
∴ =
∵∠BAE=∠DAC=135°
∴△ACD∽△ABE
∴,即
(3)∵△ACD∽△ABE
∴∠CDA=∠BEA
又∵∠AMD=∠PME
∴△AMD∽△PME
∴
∵∠PMA=∠ EMD
∴△PAM∽△EMD
∴∠APM=∠MED=90°
∴∠APC=∠CAM=90°
∵∠ACP=∠MCA
∴△ACP∽△MCA
∴ 即AC2=CM PC=18
又∵AB2+BC2=AC2,AB=BC
∴2AB2=18
∴AB=3
∴AD=BD - AB = 9-3 = 6
18.(1)由函数图象知,当时,,结合题意,此时,点与重合,
,代入,解得,则由勾股定理得,
再由函数知,当时,,即点由出发向运动时间为,
点运动的速度,;
(2)当运动时间为时,,,,
如图,作,则,,
,
,
的面积为时,解方程,得,
当或时,的面积为;
(3),,
,,
①当时,
由(2)可知,当时,的面积为,
此时,,,
,即,
时,直线将的周长与面积同时平分;
②当时,
设与交于点,作,
则有:,,
,,,,,
,,,
当时,解方程,得或(舍去),
此时,,,,,
,,
当时,不存在使得直线将的周长与面积同时平分;
综上,当时,直线将的周长与面积同时平分;当时,不存在使得直线将的周长与面积同时平分.
19.解:过Q作QE⊥AD于E,如下图所示,
在△MDN和△NEQ中,∠MDN=∠NEQ=90°,∠DMN=∠ENQ,
∴△MDN∽△NEQ,
∴=,
∴DN=×10=2,
在△MDN和△PBQ中,
,
∴△MDN≌△PBQ(ASA),
∴DM=BP,DN=BQ=2,
∴NE=AD﹣DN﹣EA=AD﹣DN﹣BQ=10﹣2﹣2=6,
∴DM=,
∴每个小正方形的面积为,
故答案为:.
20.解:
21.解:∵OA:OD=OB:OC=3:1,∠COD=∠AOB ,
∴△COD∽△BOA .
∴AB:CD=OA:OD=3:1.
∵CD=5cm,
∴AB=15cm.
∴2x+15=16.
∴x=0.5cm.
一、选择题
1.两个相似三角形的最短边分别为5 cm和3 cm,他们的周长之差为12 cm,那么大三角形的周长为( )
A.14 cm B.16 cm C.18 cm D.30 cm
2.如图,在△ABC,AB=AC=a,点D是边BC上的一点,且BD=a,AD=DC=1,则a等于( )
A. B. C.1 D.2
3.如图,在 ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则△DEF与四边形EFCO的面积比为( )
A.1:4 B.1:5 C.1:6 D.1:7
4.如图,在正方形ABCD中,点E为边AD上的一个动点(与点A、D不重合),∠EBM=45°,BE交对角线AC于点F,BM交对角线AC于点G,交边CD于点M,那么下列结论中,错误的是( )
A.△AEF∽△CBF B.△CMG∽△BFG C.△ABG∽△CFB D.△ABF∽△CBG
5.如图,中,BA=9,AC=12,点D是斜边BC上一动点,过点D分别作于点E,于点F,点G为四边形DEAF对角线交点,则线段GF的最小值为( ).
A. B. C. D.
6.如图,四边形是边长为2的正方形,点为线段上的动点,为的中点,射线交的延长线于点,过点作的垂线交于点、交的延长线于点,则以下结论:①;②;③当点与点重合时;④当时,.成立的是
A.①③④ B.②③④ C.①③ D.②④
7.如图,正方形ABCD的边长为4,延长CB至E使EB=2,以EB为边在上方作正方形EFGB,延长FG交DC于M,连接AM,AF,H为AD的中点,连接FH分别与AB,AM交于点N、K:则下列结论:①△ANH≌△GNF;②∠AFN=∠HFG;③FN=2NK;④S△AFN:S△ADM=1:4.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
8.如图,在矩形ABCD中,AB=6,BC=10,点E、F在AD边上,BF和CE交于点G,若EF=AD,则图中阴影部分的面积为( )
A.25 B.30 C.35 D.40
9.如图,△ABC是等边三角形,点D,E,F分别在AB,BC,AC边上,且AD=BE=CF,若DE⊥BC,则△DEF与△ABC的面积比为( )
A. B. C. D.
10.如图,在△ABC中,点E、F在边BC上,点E、B不重合.BE=CF,点D在边AC上,连接ED、DF,∠A=∠EDF=120°,若=m,,则m的值为( )
A. B. C. D.
二、填空题
11.如果一个三角形的三边长为5、12、13,与其相似的三角形的最长的边为39,那么较大的三角形的周长为 ,面积为 .
12.如图,已如AB=AC=DE,D为BC延长线上一点,过D作DE⊥BC于E交AC于F,若AB=m,AF=n,则AE+EF (用含m,n的式子表示).
13.如图,四边形ABCD中,AC平分∠BAD,CD⊥AD,点E为AB的中点,DE交AC于点F.若AB=,AC=,BC=1,则AF的长为 .
14.如图,△ABC中,CA=CB,点E在BC边上,点D在AC边上,连接AE、DE,若AB=AE,2∠AEB+∠ADE=180°,BE=8,CD=,则CE= .
15.如图,路灯点O到地面的垂直距离为线段OP的长.小明站在路灯下点A处,AP=4米,他的身高AB为1.6米,同学们测得他在该路灯下的影长AC为2米,路灯到地面的距离________米.
三、解答题
16.如图,在△ABC中,AB=AC,点P在BC上.
(1)在AC上求作点D,使△PCD∽△ABP;(要求:尺规作图,保留作图痕迹,不写作法)
(2)在(1)的条件下,若AB=5,BC=8,PA=PD,求CD的长.
17.如图,点A在线段BD上,在BD的同侧作等腰Rt和等腰Rt,其中∠ABC=∠AED=90°,CD与BE、AE分别交于点P、M.
(1)求证:
(2)求的值
(3)若BD=9,CP CM=18,求AD的长
18.如图①,中,,.动点以的速度由出发沿线段向运动,动点以的速度由出发沿射线运动.当点运动时,点开始运动;点到达终点时,、一起停止.设点运动的时间为,的面积为,与的函数关系图像如图②所示.
(1)点运动的速度______,______;
(2)当为何值时,的面积为;
(3)是否存在,使得直线将的周长与面积同时平分?若存在,求出的值;若不存在,请说明理由.
19.如图,已知∠DAB=∠EAC,∠ADE=∠ABC.求证:
(1)△ADE∽△ABC;
(2)=.
20.如图,在△ABC中,AD、BE是中线,它们相交于点F,EG//BC,交AD于点G.
(1)求证:△FGE∽△FDB;
(2)求AG:DF的值.
21.小明利用灯光下自己的影子长度来测量路灯的高度.如图,CD和EF是两等高的路灯,相距27m,身高1.5m的小明(AB)站在两路灯之间(D.B.F共线),被两路灯同时照射留在地面的影长BQ=4m,BP=5m.
(1)小明距离路灯多远?
(2)求路灯高度.
参考答案
1.D 2.A 3.B 4.D 5.B 6.C 7.C 8.C 9.C 10.B
11.答案为:较大三角形的周长为90,面积为270.
12.=2m﹣n.
13..
14.12.
15.答案为:10.
16.解:(1)∵AB=AC
∴∠C=∠B,
∵△PCD∽△ABP,
∴∠CPD=∠BAP,
故作∠CPD=∠BAP即可,
如图,即为所作图形,
(2)∵△PCD∽△ABP
∴
∵PA=PD
∴PC=AB=5
∴CD=BP=8-5=3
17.解:(1)证明:∵ΔABC与ΔADE均为等腰直角三角形
∴∠BAC=∠EAD=45°
∴∠CAE=90°=∠AED
∴AC∥DE
∴ △CAM∽△DEM
(2)∵ΔABC与ΔADE均为等腰直角三角形
∴,
∴ =
∵∠BAE=∠DAC=135°
∴△ACD∽△ABE
∴,即
(3)∵△ACD∽△ABE
∴∠CDA=∠BEA
又∵∠AMD=∠PME
∴△AMD∽△PME
∴
∵∠PMA=∠ EMD
∴△PAM∽△EMD
∴∠APM=∠MED=90°
∴∠APC=∠CAM=90°
∵∠ACP=∠MCA
∴△ACP∽△MCA
∴ 即AC2=CM PC=18
又∵AB2+BC2=AC2,AB=BC
∴2AB2=18
∴AB=3
∴AD=BD - AB = 9-3 = 6
18.(1)由函数图象知,当时,,结合题意,此时,点与重合,
,代入,解得,则由勾股定理得,
再由函数知,当时,,即点由出发向运动时间为,
点运动的速度,;
(2)当运动时间为时,,,,
如图,作,则,,
,
,
的面积为时,解方程,得,
当或时,的面积为;
(3),,
,,
①当时,
由(2)可知,当时,的面积为,
此时,,,
,即,
时,直线将的周长与面积同时平分;
②当时,
设与交于点,作,
则有:,,
,,,,,
,,,
当时,解方程,得或(舍去),
此时,,,,,
,,
当时,不存在使得直线将的周长与面积同时平分;
综上,当时,直线将的周长与面积同时平分;当时,不存在使得直线将的周长与面积同时平分.
19.解:过Q作QE⊥AD于E,如下图所示,
在△MDN和△NEQ中,∠MDN=∠NEQ=90°,∠DMN=∠ENQ,
∴△MDN∽△NEQ,
∴=,
∴DN=×10=2,
在△MDN和△PBQ中,
,
∴△MDN≌△PBQ(ASA),
∴DM=BP,DN=BQ=2,
∴NE=AD﹣DN﹣EA=AD﹣DN﹣BQ=10﹣2﹣2=6,
∴DM=,
∴每个小正方形的面积为,
故答案为:.
20.解:
21.解:∵OA:OD=OB:OC=3:1,∠COD=∠AOB ,
∴△COD∽△BOA .
∴AB:CD=OA:OD=3:1.
∵CD=5cm,
∴AB=15cm.
∴2x+15=16.
∴x=0.5cm.
