2021—2022学年人教版数学九年级下册27.2.2相似三角形的性质课后练习(Word版含答案)
文档属性
| 名称 | 2021—2022学年人教版数学九年级下册27.2.2相似三角形的性质课后练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 820.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-19 21:15:36 | ||
图片预览

文档简介
第二十七章 相似 27.2.2 相似三角形的性质 课后练习
一、选择题
1.如图,在正方形ABCD中,点E是边BC上的点,且CE=2BE,连接AE、DE,分别交BD、AC于点P、Q,过点P作PF⊥AE交CB的延长线于点F,下列结论:①∠AED+∠EAC+∠EDB=90°;②AP=FP;③AE=AO;④若四边形OPEQ的面积为2,则该正方形的面积为36;⑤CE·EF=EQ·DE.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
2.如图,四边形ABCD为平行四边形,E,F为CD边的两个三等分点,连接AE,BE交于点G,则S△EFG∶S△ABG=( )
A.1∶3 B.3∶1 C.1∶9 D.9∶1
3.如图,D、E分别是△ABC边AB,AC上的点,∠ADE=∠ACB,若AD=2,AB=6,AC=4,则AE的长是( )
A.1 B.2 C.3 D.4
4.如图,平行四边形ABCD中,对角线AC,BD相交于点O,点E是CD的中点,则△ODE与△AOB的面积比为( )
A.1:2 B.1:3 C.1:4 D.1:5
5.如图,在平行四边形ABCD中,点E在边DC上,DE:EC=5:2,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( )
A.5:7 B.10:4 C.25:4 D.25:49
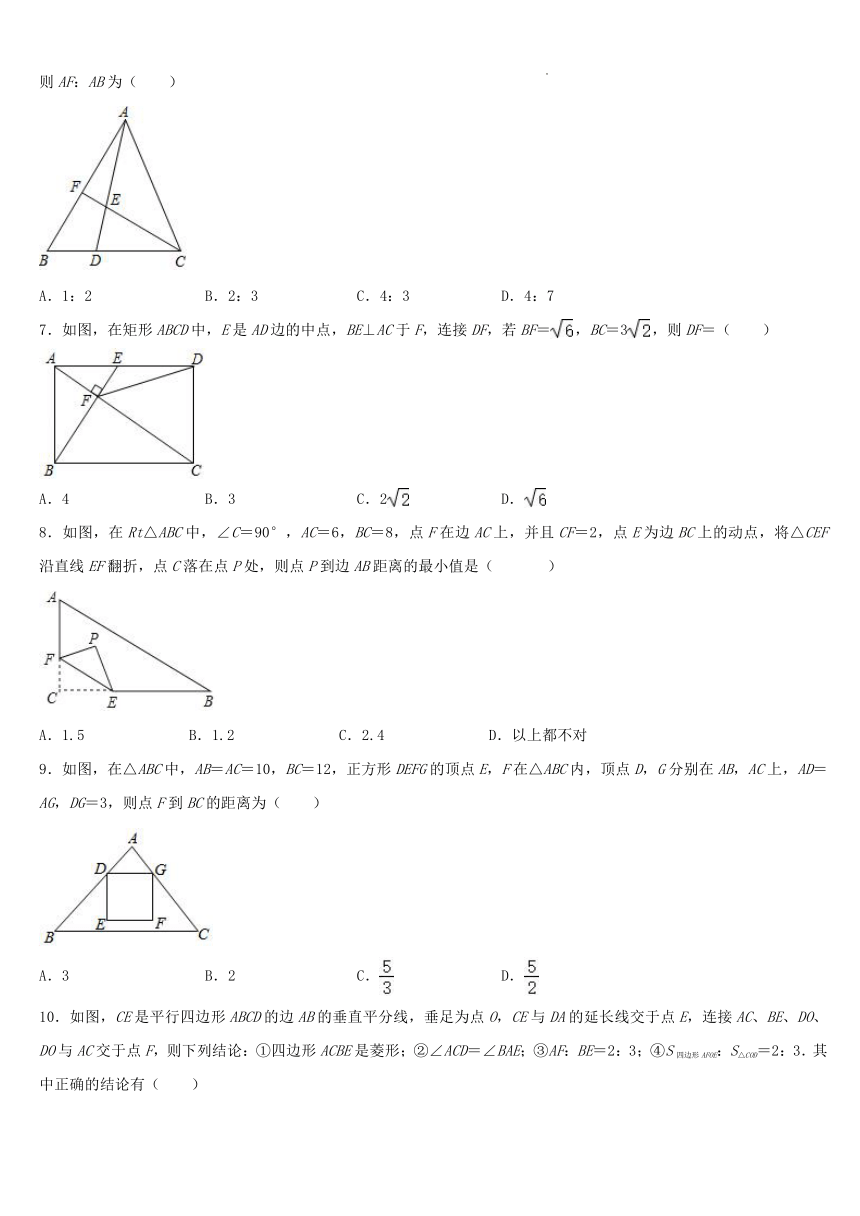
6.如图,在△ABC,D是BC上一点,BD:CD=1:2,E是AD上一点,DE:AE=1:2,连接CE,CE的延长线交AB于F,则AF:AB为( )
A.1:2 B.2:3 C.4:3 D.4:7
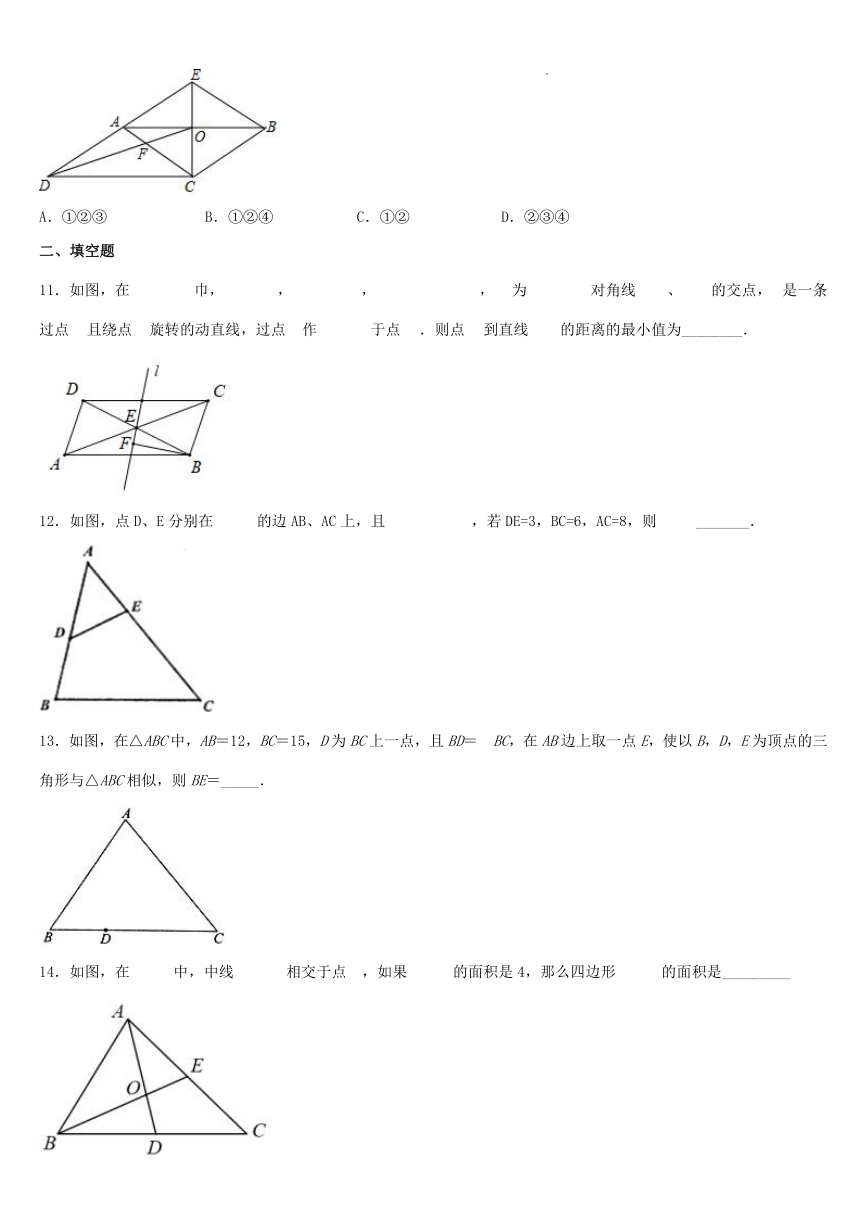
7.如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于F,连接DF,若BF=,BC=3,则DF=( )
A.4 B.3 C.2 D.
8.如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是( )
A.1.5 B.1.2 C.2.4 D.以上都不对
9.如图,在△ABC中,AB=AC=10,BC=12,正方形DEFG的顶点E,F在△ABC内,顶点D,G分别在AB,AC上,AD=AG,DG=3,则点F到BC的距离为( )
A.3 B.2 C. D.
10.如图,CE是平行四边形ABCD的边AB的垂直平分线,垂足为点O,CE与DA的延长线交于点E,连接AC、BE、DO、DO与AC交于点F,则下列结论:①四边形ACBE是菱形;②∠ACD=∠BAE;③AF:BE=2:3;④S四边形AFOE:S△COD=2:3.其中正确的结论有( )
A.①②③ B.①②④ C.①② D.②③④
二、填空题
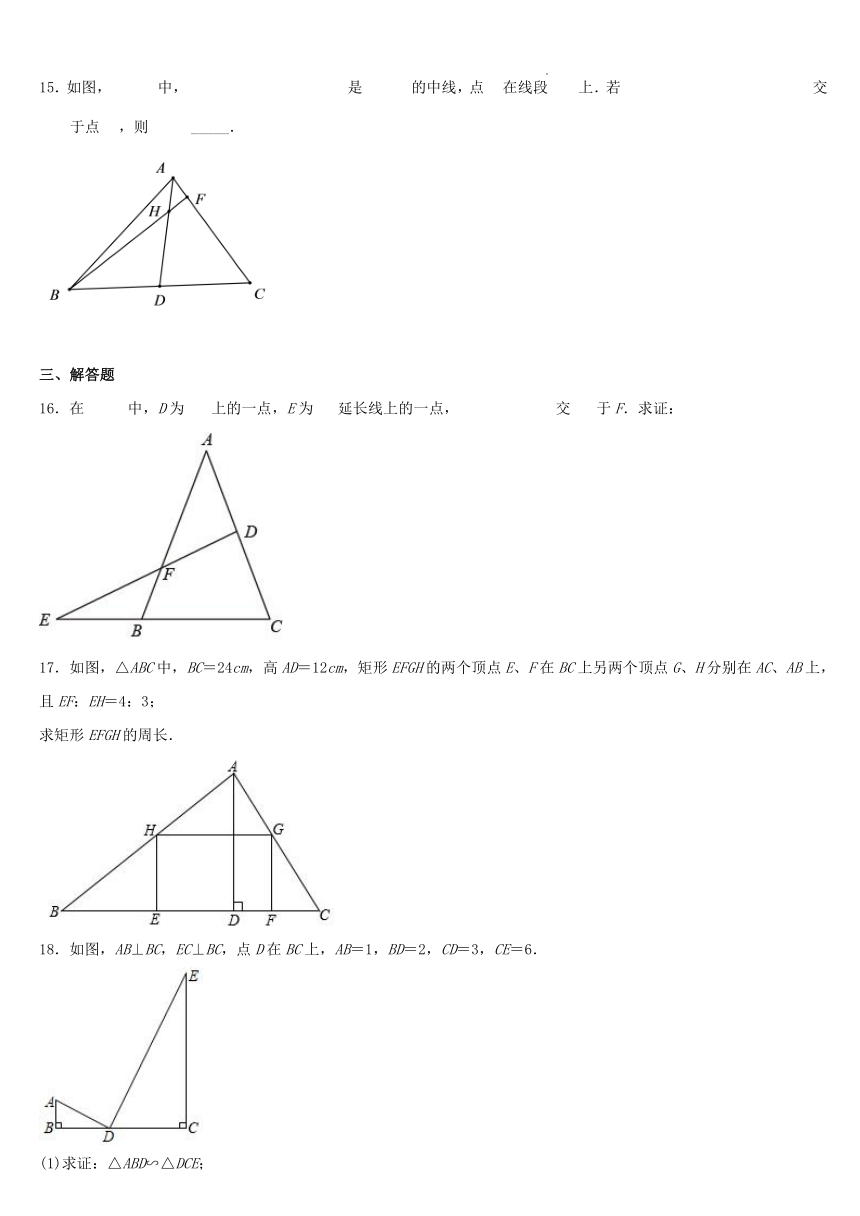
11.如图,在巾,,,,为对角线、的交点,是一条过点且绕点旋转的动直线,过点作于点.则点到直线的距离的最小值为________.
12.如图,点D、E分别在的边AB、AC上,且,若DE=3,BC=6,AC=8,则_______.
13.如图,在△ABC中,AB=12,BC=15,D为BC上一点,且BD=BC,在AB边上取一点E,使以B,D,E为顶点的三角形与△ABC相似,则BE=_____.
14.如图,在中,中线相交于点,如果的面积是4,那么四边形的面积是_________
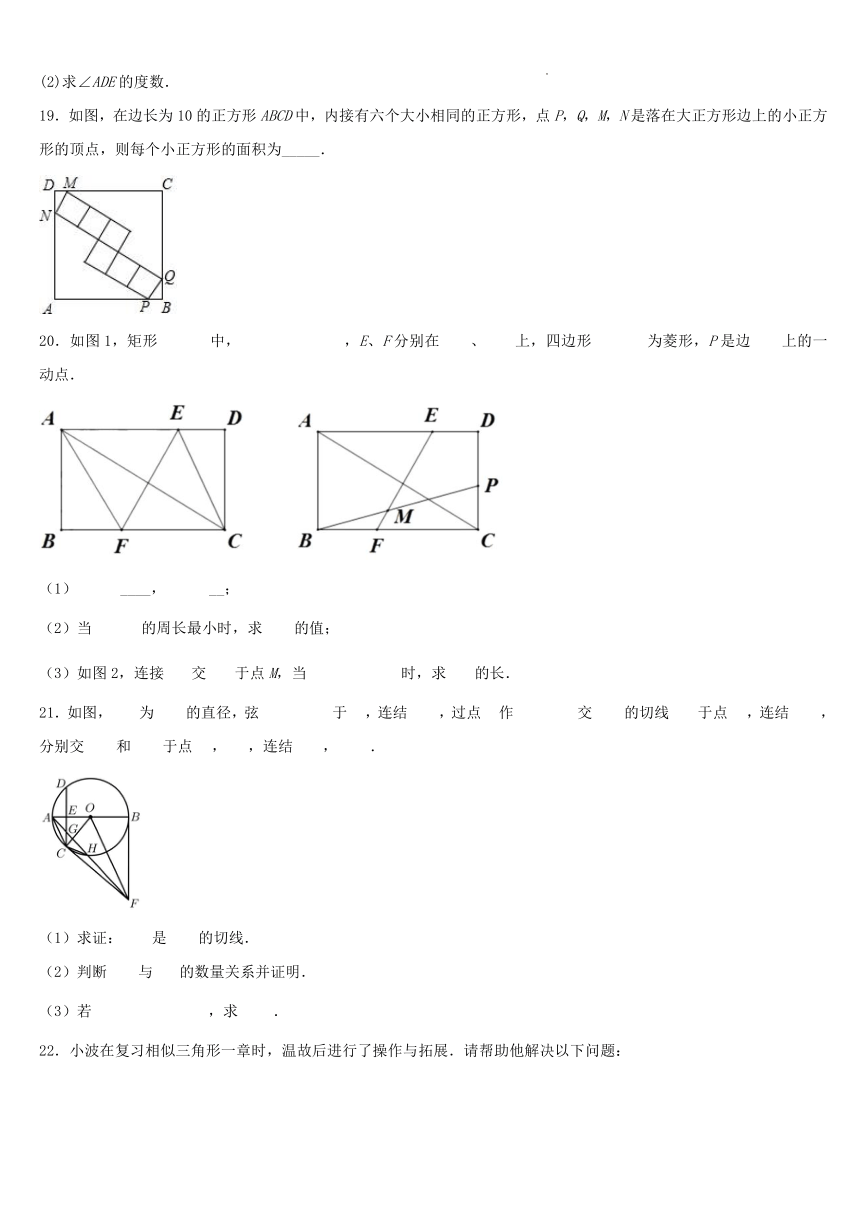
15.如图,中,是的中线,点在线段上.若交于点,则_____.
三、解答题
16.在中,D为上的一点,E为延长线上的一点,交于F.求证:
17.如图,△ABC中,BC=24cm,高AD=12cm,矩形EFGH的两个顶点E、F在BC上另两个顶点G、H分别在AC、AB上,且EF:EH=4:3;
求矩形EFGH的周长.
18.如图,AB⊥BC,EC⊥BC,点D在BC上,AB=1,BD=2,CD=3,CE=6.
(1)求证:△ABD∽△DCE;
(2)求∠ADE的度数.
19.如图,在边长为10的正方形ABCD中,内接有六个大小相同的正方形,点P,Q,M,N是落在大正方形边上的小正方形的顶点,则每个小正方形的面积为_____.
20.如图1,矩形中,,E、F分别在、上,四边形为菱形,P是边上的一动点.
(1)____,__;
(2)当的周长最小时,求的值;
(3)如图2,连接交于点M,当时,求的长.
21.如图,为的直径,弦于,连结,过点作交的切线于点,连结,分别交和于点,,连结,.
(1)求证:是的切线.
(2)判断与的数量关系并证明.
(3)若 ,求.
22.小波在复习相似三角形一章时,温故后进行了操作与拓展.请帮助他解决以下问题:
(1)小波想作出一个内接于最大正方形.如图1,在中,边上的高为4.他先在边上任取了一点,作出正方形,使在边上,在内,请你在及其内部,以点B为位似中心作正方形的位似正方形,且使正方形的面积最大(不要求写作法).
(2)求(1)中作出的正方形的边长.
(3)在(2)的条件下,在射线上截取,连结(如图2).当时,猜想的度数,并尝试证明.
23.已知和,,连结.
感知:如图①,当点E在边上时,试判断线段之间的关系是_______.
探究:将图①中的绕点A旋转至如图②所示位置时,探究线段之间的关系,并说明理由;
应用:将图①中的绕点A旋转至与直线垂直,直线交直线于点F,若,请直接写出线段的长度.
【参考答案】
1.B2.C 3.C 4.A 5.D 6.D 7.B 8.B 9.A 10.B
11.
12.4
13.4或
14.8
15.
16.证明:过D作交于G,则和相似,
∴,
∵,
∴,
由可得和相似,
∴即,
∴
17.解:设AD与HG的交点为K,如图所示,
设厘米,厘米,则;
,
.
,即.
解得:;
,.
矩形的周长.
18.(1)证明:∵AB⊥BC,EC⊥BC,点D在BC上,
∴∠ABD=∠DCE=90°.
∵AB=1,BD=2,CD=3,CE=6,
∴=,=.
∴=.
∴△ABD∽△DCE;
(2)由(1)知,△ABD∽△DCE,则∠BAD=∠EDC.
∵∠BAD+∠ADB=90°,
∴∠ADB+∠EDC=90°.
∴∠ADE=180°﹣∠ADB﹣∠EDC=90°.
20.证明:(1)
四边形是矩形,
,,∠B=90°,
∴AC=,
∵平行四边形是菱形,
∴AF=CF,
设AF=x,在Rt△ABF时, AF2=AB2+BF2,
∴x2=22+(4-x)2,解得 x=,
故答案为:,;
(2)如图,作点关于的对称点Q,连接EQ,交于点,此时的周长最小,
四边形是菱形,
由(2)知,
,
点,点Q关于对称,
,
,
故答案为:;
(3)如图,延长,延长交于点,过点作于,交于点,过点作于点,
由(2)可知,,,
,,
四边形是矩形
,,
,
,
,
,
,
,
,,
,,
,,
,
,
,
,
,,
,
,
,
,
,
,
,
,
,
,
,
.
21.(1)∵,
∴,,
∵,∴,∴,
在与中,
∴,∴,
∵为切线,
∴,即,
∴,即,又∵在上,
∴是的切线.
(2)∵,,∴,
∴,∴,
∵,为直径,
∴(垂径定理),
∴,又∵,
∴, ∴,
∵为切线,
∴(弦切角定理),又∵,
∴,∴①,又∵,
由(1)得:,
∴②,
由①②得:,即:,又∵,
∴.
(3)∵,
∴设,,则,,,
由勾股定理得:,
由(2)得:,
∴
在中,,,
由勾股定理得:,
在中,,,
由勾股定理得,
由(2)得:,
∴,即,
∴,∴.
22.(1)如图:正方形即为所求;
(2)如图:过A作AD⊥BC,垂足为D
∵PQMN是正方形
∴AE=AD-ED=AD-PN
∵PN//BC,
∴△APN∽△ABC,
∴,即,解得PN=;
(3)∠QEM=,证明如下:
证明:如图:
由,则可设MN=3k,BM=4k,则BN=5k,BQ=k,BE=2k,
∴
∴
∵∠QBE=∠EBM
∴△BQE∽△BEM
∴∠BEQ=∠BME
∵NE=NM
∴∠NEM=∠NME
∵∠BME+∠EMN=90°
∴∠BEQ+∠NEM=90°
∴∠QEM=90°.
23.(1),
在△ABD和△ACE中,
∴△ABD≌△ACE (SAS),
∴BD=CE,BD⊥EC.
故答案为:BD=CE,BD⊥EC.
(2)结论:.
如图1,延长线段CE交AB于点G,交BD点于H.
∵∠BAC=∠DAE=90°,
即∠CAE+∠BAE=∠DAB+∠BAE=90°,
∴∠DAB=∠CAE.
在△ABD和△ACE中,
∴△ABD ≌△ACE(SAS),
∴BD=CE,∠ABD=∠ACE,
∵∠BGH=∠AGC,∠AGC+∠ACE=∠BAC=90°
∴∠BGH+∠ABD=90°
∴∠BHG=90°,
∴BD⊥CE.
(3)或;
如图2所示,当DE在AB左边时,设CA延长线与DE交于点M,AB与CE交于点N,
∵DE与直线AC垂直,∠BAC=∠DAE=90°,AB=AC, AD=AE,AB=15,AD=,
∴DE=10,AM=ME=5, ∴CE=,
可证△ACN ∽△MCE,
得 ,
∴ ,
∴ ,
∴,
再证△BFN ∽△CME,
得,
∴,
∴BF=;
如图3所示,当DE在AB右边时,设AC与DE交于点M,BA延长线与CE延长线交于点N,
∵DE与直线AC垂直,∠BAC=∠DAE=90°,AB=AC, AD=AE,AB=15,AD=,
∴DE=10,AM=ME=5,∴CE=,
可证△ACN ∽△MCE,
得,
∴,
∴,
∴,
再证△BFN ∽△CME,
得,
∴,
∴BF=.
一、选择题
1.如图,在正方形ABCD中,点E是边BC上的点,且CE=2BE,连接AE、DE,分别交BD、AC于点P、Q,过点P作PF⊥AE交CB的延长线于点F,下列结论:①∠AED+∠EAC+∠EDB=90°;②AP=FP;③AE=AO;④若四边形OPEQ的面积为2,则该正方形的面积为36;⑤CE·EF=EQ·DE.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
2.如图,四边形ABCD为平行四边形,E,F为CD边的两个三等分点,连接AE,BE交于点G,则S△EFG∶S△ABG=( )
A.1∶3 B.3∶1 C.1∶9 D.9∶1
3.如图,D、E分别是△ABC边AB,AC上的点,∠ADE=∠ACB,若AD=2,AB=6,AC=4,则AE的长是( )
A.1 B.2 C.3 D.4
4.如图,平行四边形ABCD中,对角线AC,BD相交于点O,点E是CD的中点,则△ODE与△AOB的面积比为( )
A.1:2 B.1:3 C.1:4 D.1:5
5.如图,在平行四边形ABCD中,点E在边DC上,DE:EC=5:2,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( )
A.5:7 B.10:4 C.25:4 D.25:49
6.如图,在△ABC,D是BC上一点,BD:CD=1:2,E是AD上一点,DE:AE=1:2,连接CE,CE的延长线交AB于F,则AF:AB为( )
A.1:2 B.2:3 C.4:3 D.4:7
7.如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于F,连接DF,若BF=,BC=3,则DF=( )
A.4 B.3 C.2 D.
8.如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是( )
A.1.5 B.1.2 C.2.4 D.以上都不对
9.如图,在△ABC中,AB=AC=10,BC=12,正方形DEFG的顶点E,F在△ABC内,顶点D,G分别在AB,AC上,AD=AG,DG=3,则点F到BC的距离为( )
A.3 B.2 C. D.
10.如图,CE是平行四边形ABCD的边AB的垂直平分线,垂足为点O,CE与DA的延长线交于点E,连接AC、BE、DO、DO与AC交于点F,则下列结论:①四边形ACBE是菱形;②∠ACD=∠BAE;③AF:BE=2:3;④S四边形AFOE:S△COD=2:3.其中正确的结论有( )
A.①②③ B.①②④ C.①② D.②③④
二、填空题
11.如图,在巾,,,,为对角线、的交点,是一条过点且绕点旋转的动直线,过点作于点.则点到直线的距离的最小值为________.
12.如图,点D、E分别在的边AB、AC上,且,若DE=3,BC=6,AC=8,则_______.
13.如图,在△ABC中,AB=12,BC=15,D为BC上一点,且BD=BC,在AB边上取一点E,使以B,D,E为顶点的三角形与△ABC相似,则BE=_____.
14.如图,在中,中线相交于点,如果的面积是4,那么四边形的面积是_________
15.如图,中,是的中线,点在线段上.若交于点,则_____.
三、解答题
16.在中,D为上的一点,E为延长线上的一点,交于F.求证:
17.如图,△ABC中,BC=24cm,高AD=12cm,矩形EFGH的两个顶点E、F在BC上另两个顶点G、H分别在AC、AB上,且EF:EH=4:3;
求矩形EFGH的周长.
18.如图,AB⊥BC,EC⊥BC,点D在BC上,AB=1,BD=2,CD=3,CE=6.
(1)求证:△ABD∽△DCE;
(2)求∠ADE的度数.
19.如图,在边长为10的正方形ABCD中,内接有六个大小相同的正方形,点P,Q,M,N是落在大正方形边上的小正方形的顶点,则每个小正方形的面积为_____.
20.如图1,矩形中,,E、F分别在、上,四边形为菱形,P是边上的一动点.
(1)____,__;
(2)当的周长最小时,求的值;
(3)如图2,连接交于点M,当时,求的长.
21.如图,为的直径,弦于,连结,过点作交的切线于点,连结,分别交和于点,,连结,.
(1)求证:是的切线.
(2)判断与的数量关系并证明.
(3)若 ,求.
22.小波在复习相似三角形一章时,温故后进行了操作与拓展.请帮助他解决以下问题:
(1)小波想作出一个内接于最大正方形.如图1,在中,边上的高为4.他先在边上任取了一点,作出正方形,使在边上,在内,请你在及其内部,以点B为位似中心作正方形的位似正方形,且使正方形的面积最大(不要求写作法).
(2)求(1)中作出的正方形的边长.
(3)在(2)的条件下,在射线上截取,连结(如图2).当时,猜想的度数,并尝试证明.
23.已知和,,连结.
感知:如图①,当点E在边上时,试判断线段之间的关系是_______.
探究:将图①中的绕点A旋转至如图②所示位置时,探究线段之间的关系,并说明理由;
应用:将图①中的绕点A旋转至与直线垂直,直线交直线于点F,若,请直接写出线段的长度.
【参考答案】
1.B2.C 3.C 4.A 5.D 6.D 7.B 8.B 9.A 10.B
11.
12.4
13.4或
14.8
15.
16.证明:过D作交于G,则和相似,
∴,
∵,
∴,
由可得和相似,
∴即,
∴
17.解:设AD与HG的交点为K,如图所示,
设厘米,厘米,则;
,
.
,即.
解得:;
,.
矩形的周长.
18.(1)证明:∵AB⊥BC,EC⊥BC,点D在BC上,
∴∠ABD=∠DCE=90°.
∵AB=1,BD=2,CD=3,CE=6,
∴=,=.
∴=.
∴△ABD∽△DCE;
(2)由(1)知,△ABD∽△DCE,则∠BAD=∠EDC.
∵∠BAD+∠ADB=90°,
∴∠ADB+∠EDC=90°.
∴∠ADE=180°﹣∠ADB﹣∠EDC=90°.
20.证明:(1)
四边形是矩形,
,,∠B=90°,
∴AC=,
∵平行四边形是菱形,
∴AF=CF,
设AF=x,在Rt△ABF时, AF2=AB2+BF2,
∴x2=22+(4-x)2,解得 x=,
故答案为:,;
(2)如图,作点关于的对称点Q,连接EQ,交于点,此时的周长最小,
四边形是菱形,
由(2)知,
,
点,点Q关于对称,
,
,
故答案为:;
(3)如图,延长,延长交于点,过点作于,交于点,过点作于点,
由(2)可知,,,
,,
四边形是矩形
,,
,
,
,
,
,
,
,,
,,
,,
,
,
,
,
,,
,
,
,
,
,
,
,
,
,
,
,
.
21.(1)∵,
∴,,
∵,∴,∴,
在与中,
∴,∴,
∵为切线,
∴,即,
∴,即,又∵在上,
∴是的切线.
(2)∵,,∴,
∴,∴,
∵,为直径,
∴(垂径定理),
∴,又∵,
∴, ∴,
∵为切线,
∴(弦切角定理),又∵,
∴,∴①,又∵,
由(1)得:,
∴②,
由①②得:,即:,又∵,
∴.
(3)∵,
∴设,,则,,,
由勾股定理得:,
由(2)得:,
∴
在中,,,
由勾股定理得:,
在中,,,
由勾股定理得,
由(2)得:,
∴,即,
∴,∴.
22.(1)如图:正方形即为所求;
(2)如图:过A作AD⊥BC,垂足为D
∵PQMN是正方形
∴AE=AD-ED=AD-PN
∵PN//BC,
∴△APN∽△ABC,
∴,即,解得PN=;
(3)∠QEM=,证明如下:
证明:如图:
由,则可设MN=3k,BM=4k,则BN=5k,BQ=k,BE=2k,
∴
∴
∵∠QBE=∠EBM
∴△BQE∽△BEM
∴∠BEQ=∠BME
∵NE=NM
∴∠NEM=∠NME
∵∠BME+∠EMN=90°
∴∠BEQ+∠NEM=90°
∴∠QEM=90°.
23.(1),
在△ABD和△ACE中,
∴△ABD≌△ACE (SAS),
∴BD=CE,BD⊥EC.
故答案为:BD=CE,BD⊥EC.
(2)结论:.
如图1,延长线段CE交AB于点G,交BD点于H.
∵∠BAC=∠DAE=90°,
即∠CAE+∠BAE=∠DAB+∠BAE=90°,
∴∠DAB=∠CAE.
在△ABD和△ACE中,
∴△ABD ≌△ACE(SAS),
∴BD=CE,∠ABD=∠ACE,
∵∠BGH=∠AGC,∠AGC+∠ACE=∠BAC=90°
∴∠BGH+∠ABD=90°
∴∠BHG=90°,
∴BD⊥CE.
(3)或;
如图2所示,当DE在AB左边时,设CA延长线与DE交于点M,AB与CE交于点N,
∵DE与直线AC垂直,∠BAC=∠DAE=90°,AB=AC, AD=AE,AB=15,AD=,
∴DE=10,AM=ME=5, ∴CE=,
可证△ACN ∽△MCE,
得 ,
∴ ,
∴ ,
∴,
再证△BFN ∽△CME,
得,
∴,
∴BF=;
如图3所示,当DE在AB右边时,设AC与DE交于点M,BA延长线与CE延长线交于点N,
∵DE与直线AC垂直,∠BAC=∠DAE=90°,AB=AC, AD=AE,AB=15,AD=,
∴DE=10,AM=ME=5,∴CE=,
可证△ACN ∽△MCE,
得,
∴,
∴,
∴,
再证△BFN ∽△CME,
得,
∴,
∴BF=.
