2021—2022学年人教版八年级数学下册18.1.1平行四边形的判定提高练习(Word版含答案)
文档属性
| 名称 | 2021—2022学年人教版八年级数学下册18.1.1平行四边形的判定提高练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 347.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-19 21:15:41 | ||
图片预览



文档简介
18.1.1平行四边形的判定提高练习
2021—2022学年人教版八年级数学下册
一、单选题
1.如图,在 ABCD中,AE⊥BC于点E,AF⊥CD于点F,若AE=4,AF=6,且 ABCD的周长为40,则 ABCD的面积为( )
A.24 B.36 C.40 D.48
2.证明:平行四边形的对角线互相平分
已知:如图,四边形ABCD是平行四边形,对角线AC,BD相交于点O
求证:OA=OC,OB=OD
证明:∵四边形ABCD是平行四边形,
∴…
∴∠ABO=∠CDO,∠BAO=∠DCO,
∴△AOB≌△COD,
∴OA=OC,OB=OD
其中,在“四边形ABCD是平行四边形”与“∠ABO=∠CDO,∠BAO=∠DCO”之间应补充的步骤是( )
A.AB=CD,AD=BC B.AD//BC,AD=BC
C.AB//CD,AD//BC D.AB//CD,AB=CD
3.如图,已知四边形ABCD和四边形BCEF均为平行四边形,∠D=60°,连接AF,并延长交BE于点P,若AP⊥BE,AB=3,BC=2,AF=1,则BE的长为( )
A.5 B.2 C.2 D.3
4.如图,有两块全等的含角的直角三角板,将它们拼成形状不同的平行四边形,则最多可以拼成( )
A.1种 B.2种 C.3种 D.4种
5.如图,若AB//CD,AC交BD于点O,则下列条件中不能说明四边形ABCD是平行四边形的是( )
A.AD∥BC B.OA=OC C.AD=AB D.AB=CD
6.在下列条件中能判定四边形ABCD是平行四边形的是( )
A.AB=BC,AD=DC B.AB∥CD,AD=BC
C.AB∥CD,∠B=∠D D.∠A=∠B,∠C=∠D
7.给定不在同一直线上的三点,则以这三点为顶点的平行四边形有( )
A.1个 B.2个 C.3个 D.4个
8.在中,、分别在、上,若想使四边形为平行四边形,须添加一个条件,这个条件可以是( )
①;②;③;④.
A.①或② B.②或③ C.③或④ D.①或③或④
9.下列给出的条件能判定四边形 ABCD为平行四边形的是 ( )
A.AB//CD,AD=BC B.∠A=∠B,∠C=∠D
C.AB=CD,AD=BC D.AB=AD,CB=CD
10.平行四边形的一边长为12,那么这个平行四边形的两条对角线的长可能是( )
A.8和12 B.9和13 C.12和12 D.11和14
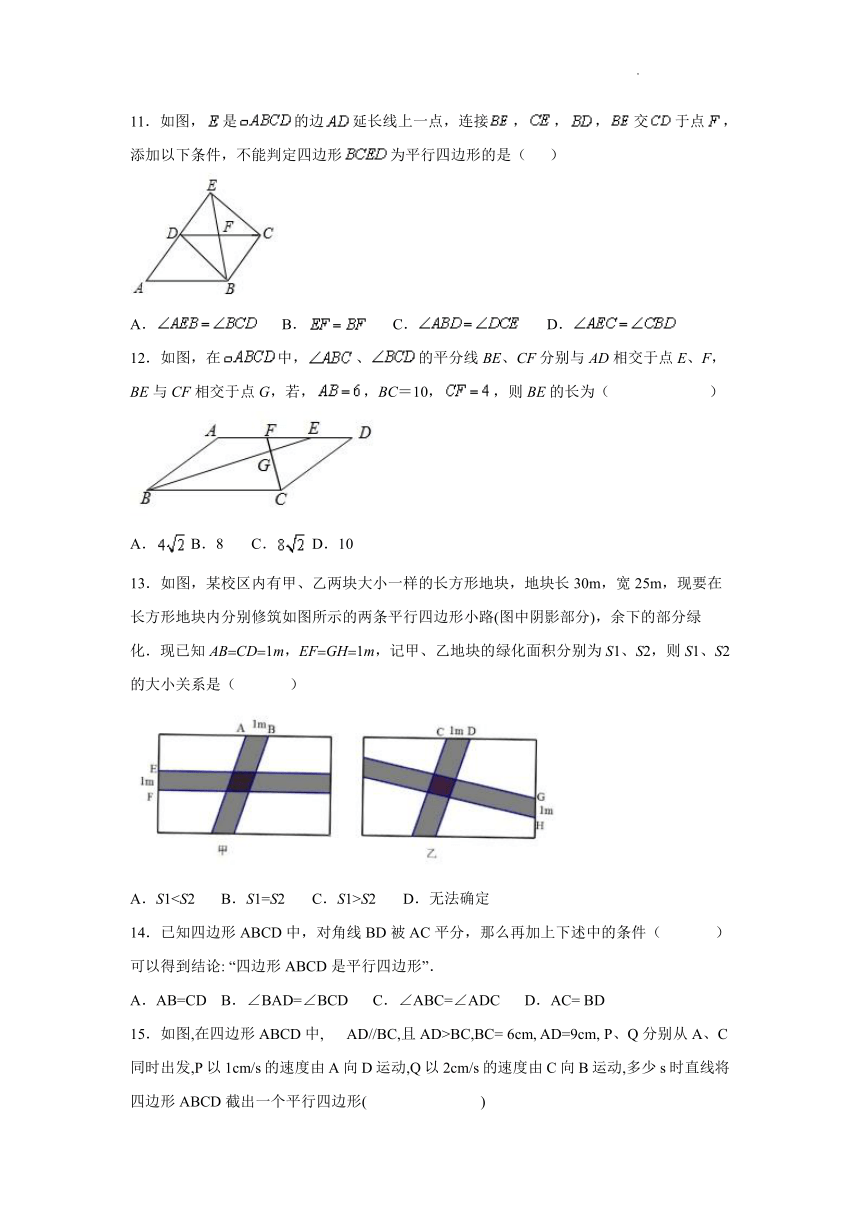
11.如图,是的边延长线上一点,连接,,,交于点,添加以下条件,不能判定四边形为平行四边形的是( )
A. B. C. D.
12.如图,在中,、的平分线BE、CF分别与AD相交于点E、F,BE与CF相交于点G,若,,BC=10,,则BE的长为( )
A. B.8 C. D.10
13.如图,某校区内有甲、乙两块大小一样的长方形地块,地块长30m,宽25m,现要在长方形地块内分别修筑如图所示的两条平行四边形小路(图中阴影部分),余下的部分绿化.现已知AB CD 1m,EF GH 1m,记甲、乙地块的绿化面积分别为S1、S2,则S1、S2的大小关系是( )
A.S1S2 D.无法确定
14.已知四边形ABCD中,对角线BD被AC平分,那么再加上下述中的条件( ) 可以得到结论: “四边形ABCD是平行四边形”.
A.AB=CD B.∠BAD=∠BCD C.∠ABC=∠ADC D.AC= BD
15.如图,在四边形ABCD中, AD//BC,且AD>BC,BC= 6cm, AD=9cm, P、Q分别从A、C同时出发,P以1cm/s的速度由A向D运动,Q以2cm/s的速度由C向B运动,多少s时直线将四边形ABCD截出一个平行四边形( )
A.1 B.2 C.3 D.2或3
二、填空题
16.若是不在同一条直线的三点,则以这三点为顶点画平行四边形,可画_____个.
17.在四边形ABCD中,AB=CD,请添加一个条件_____,使得四边形ABCD是平行四边形.
18.如图,在平行四边形中,相交于点O,点E,F在对角线上,有下列条件:①;②;③;④.其中一定能判定四边形是平行四边形的是______.
19.如图,在等腰梯形 ABCD 中,AD∥BC,AB=CD.点 P 为底边 BC 的延长线上任意一点,PE⊥AB 于 E,PF⊥DC 于 F,BM⊥DC 于 M.请你探究线段 PE、PF、BM 之间的数量关系:
______.
20.已知:一组邻边分别为和的平行四边形,和的平分线分别交所在直线于点,,则线段的长为________.
三、解答题
21.如图,已知四边形,请在下列三个关系中,选出两个恰当的关系作为条件,推出四边形是平行四边形,并予以证明.
关系:①,②, ③
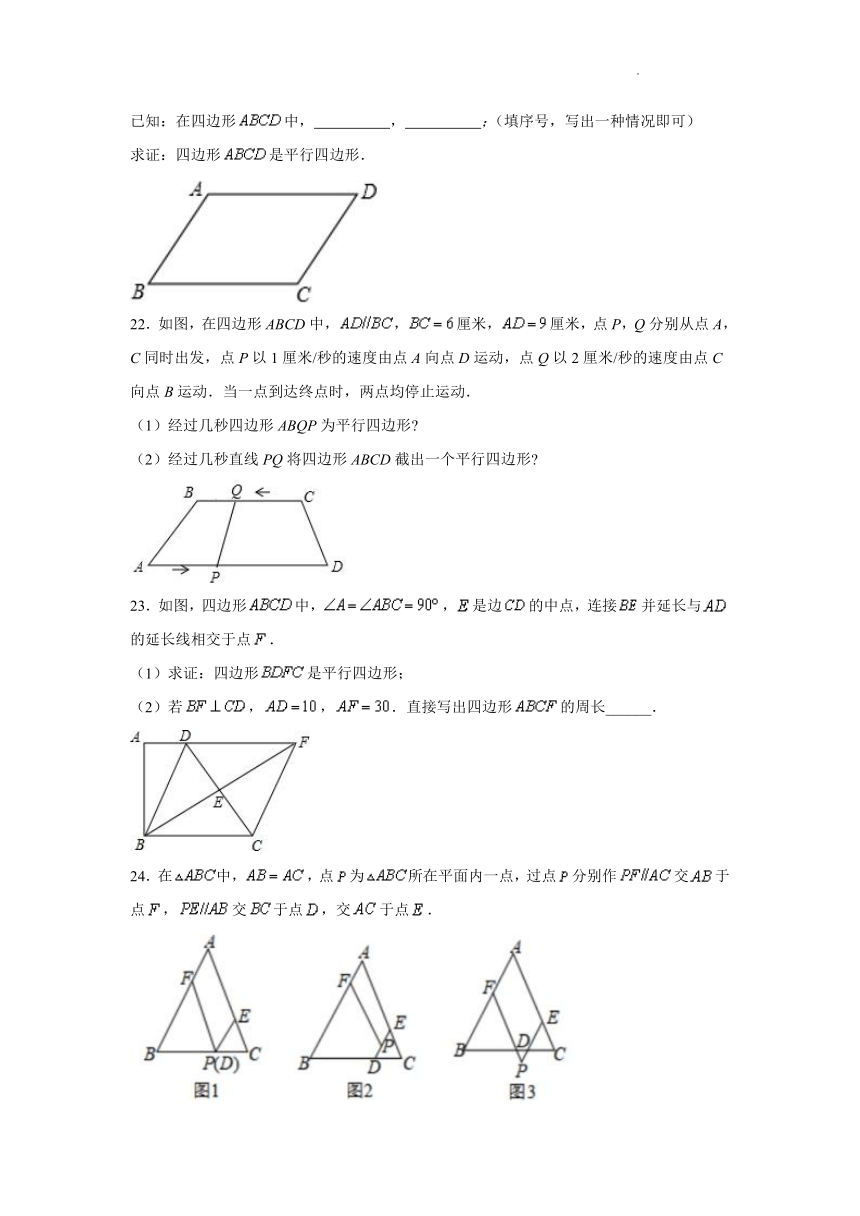
已知:在四边形中, , ;(填序号,写出一种情况即可)
求证:四边形是平行四边形.
22.如图,在四边形ABCD中,,厘米,厘米,点P,Q分别从点A,C同时出发,点P以1厘米/秒的速度由点A向点D运动,点Q以2厘米/秒的速度由点C向点B运动.当一点到达终点时,两点均停止运动.
(1)经过几秒四边形ABQP为平行四边形
(2)经过几秒直线PQ将四边形ABCD截出一个平行四边形
23.如图,四边形中,,是边的中点,连接并延长与的延长线相交于点.
(1)求证:四边形是平行四边形;
(2)若,,.直接写出四边形的周长______.
24.在中,,点为所在平面内一点,过点分别作交于点,交于点,交于点.
(1)如图1,当点在边上时,请探索线段,,之间的数量关系,并证明你的结论.
(2)如图2,当点在内部时,线段,,,之间有怎样的数量关系?请说明理由.
(3)如图3,当点在外部时,线段,,,之间有怎样的数量关系?直接写出结论.
25.如图,中,,连结,是边上一点,连结交于点.
(1)如图1,连结,若,,求的面积;
(2)如图2,延长至点,连结、,点在上,且,,过作于点.若,求证:
参考答案:
1--10DDDCC CCDCD 11---15ACCBD
16.
17.AB//CD等
18.①④
19.PE-PF=BM.
20.或
21.(1)解:选择:①,③,
证明:∵∠B+∠C=180°, ∴AB∥DC,
又∵AD∥BC,
∴四边形ABCD是平行四边形;
故答案为:AD∥BC,∠A=∠C.
22.解:(1)设经过t秒四边形ABQP是平行四边形,
根据题意,得AP=t厘米,CQ=2t厘米,
则BQ=(6-2t)厘米,
∵AD∥BC,
∴当AP=BQ时,四边形ABQP是平行四边形,
∴t=6-2t,
解得t=2,
即经过2秒四边形ABQP为平行四边形;
(2)由(1)知,经过2秒四边形ABQP是平行四边形,设经过x秒直线PQ将四边形ABCD截出另一个平行四边形DCQP,
根据题意,得AP=x厘米,CQ=2x厘米,
则PD=(9-x)厘米,
∵AD∥BC,
∴当CQ=PD时,四边形DCQP是平行四边形,
∴2x=9-x,
解得x=3.
综上,经过2秒或3秒直线PQ将四边形ABCD截出一个平行四边形.
23.(1)证明:∵∠A=∠ABC=90°,
∴BC∥AD,
∴∠CBE=∠DFE,
在△BEC与△FED中,
,
∴△BEC≌△FED,
∴BE=FE,
又∵E是边CD的中点,
∴CE=DE,
∴四边形BDFC是平行四边形;
(2)∵BF⊥CD,四边形BDFC是平行四边形,
∴四边形BDFC是菱形,
∵AD=10cm,AF=30cm,
∴DF=30-10=20cm,
∴BD=BC=CF=DF=20cm,
∵在Rt△BAD中,
AB=cm,
∴四边形ABCF的周长是30+20×2+=70+(cm).
故四边形ABCF的周长是(70+)cm.
24.解:(1)PE+PF=AB.
证明:∵,
∴四边形FPEA为平行四边形
∴PF=AE,PE=AF
∵
∴∠EPB=∠C
∵AB=AC
∴∠B=∠C
∴∠EPB=∠B
∴BF=FP
∴AB=AF+FB=PE+FB=PE+FP=PE+AE
∴PE+PF=AB.
(2).
证明:∵,
∴四边形FPEA为平行四边形
∴PF=AE,PE=AF
∵
∴∠B=∠EDC
∵∠B=∠C
∴∠EDC=∠C
∴ED=EC
∴AB=AC=AE+EC=FP+ED=PF+PD+PE
∴.
(3).
证明:∵,
∴四边形FPEA为平行四边形
∴PF=AE,PE=AF
∵
∴∠B=∠EDC
∵∠B=∠C
∴∠EDC=∠C
∴ED=EC
∴AB=AC=AE+EC=PF+ED=PF+PE-PD
∴.
25.解:(1)
如图:过A点作AN⊥BE,交BE于N.
∵,
∴△ABE为等边三角形,
∴AB=BE=AE=6
即:AN=
∵
∴
∵BE=6
∴BC=10
∴EC=4
∴
即:的面积为.
(2)
如图:延长GD至P使DP=BG,连接AP,
∵AH=AF,
∴∠AFH=∠AHF
即:∠AFB=∠AHD,
又∵AF=AH,BF=DH,
∴≌
∴AB=AD
又∵,,
∴∠ABG=∠ADP
∵BG=DP,
∴≌
∴AG=AP,∠BAG=∠DAP
∵∠ABC=60°
∴∠BAD=120°
即:∠GAP=120°
∴∠AGP=∠APG=60°,
又∵AM⊥GD
∴GP=2GM=AG,
∵BG=GP
∴BG+GD=GD+DP=GP
即:BG+GD=AG.
2021—2022学年人教版八年级数学下册
一、单选题
1.如图,在 ABCD中,AE⊥BC于点E,AF⊥CD于点F,若AE=4,AF=6,且 ABCD的周长为40,则 ABCD的面积为( )
A.24 B.36 C.40 D.48
2.证明:平行四边形的对角线互相平分
已知:如图,四边形ABCD是平行四边形,对角线AC,BD相交于点O
求证:OA=OC,OB=OD
证明:∵四边形ABCD是平行四边形,
∴…
∴∠ABO=∠CDO,∠BAO=∠DCO,
∴△AOB≌△COD,
∴OA=OC,OB=OD
其中,在“四边形ABCD是平行四边形”与“∠ABO=∠CDO,∠BAO=∠DCO”之间应补充的步骤是( )
A.AB=CD,AD=BC B.AD//BC,AD=BC
C.AB//CD,AD//BC D.AB//CD,AB=CD
3.如图,已知四边形ABCD和四边形BCEF均为平行四边形,∠D=60°,连接AF,并延长交BE于点P,若AP⊥BE,AB=3,BC=2,AF=1,则BE的长为( )
A.5 B.2 C.2 D.3
4.如图,有两块全等的含角的直角三角板,将它们拼成形状不同的平行四边形,则最多可以拼成( )
A.1种 B.2种 C.3种 D.4种
5.如图,若AB//CD,AC交BD于点O,则下列条件中不能说明四边形ABCD是平行四边形的是( )
A.AD∥BC B.OA=OC C.AD=AB D.AB=CD
6.在下列条件中能判定四边形ABCD是平行四边形的是( )
A.AB=BC,AD=DC B.AB∥CD,AD=BC
C.AB∥CD,∠B=∠D D.∠A=∠B,∠C=∠D
7.给定不在同一直线上的三点,则以这三点为顶点的平行四边形有( )
A.1个 B.2个 C.3个 D.4个
8.在中,、分别在、上,若想使四边形为平行四边形,须添加一个条件,这个条件可以是( )
①;②;③;④.
A.①或② B.②或③ C.③或④ D.①或③或④
9.下列给出的条件能判定四边形 ABCD为平行四边形的是 ( )
A.AB//CD,AD=BC B.∠A=∠B,∠C=∠D
C.AB=CD,AD=BC D.AB=AD,CB=CD
10.平行四边形的一边长为12,那么这个平行四边形的两条对角线的长可能是( )
A.8和12 B.9和13 C.12和12 D.11和14
11.如图,是的边延长线上一点,连接,,,交于点,添加以下条件,不能判定四边形为平行四边形的是( )
A. B. C. D.
12.如图,在中,、的平分线BE、CF分别与AD相交于点E、F,BE与CF相交于点G,若,,BC=10,,则BE的长为( )
A. B.8 C. D.10
13.如图,某校区内有甲、乙两块大小一样的长方形地块,地块长30m,宽25m,现要在长方形地块内分别修筑如图所示的两条平行四边形小路(图中阴影部分),余下的部分绿化.现已知AB CD 1m,EF GH 1m,记甲、乙地块的绿化面积分别为S1、S2,则S1、S2的大小关系是( )
A.S1
14.已知四边形ABCD中,对角线BD被AC平分,那么再加上下述中的条件( ) 可以得到结论: “四边形ABCD是平行四边形”.
A.AB=CD B.∠BAD=∠BCD C.∠ABC=∠ADC D.AC= BD
15.如图,在四边形ABCD中, AD//BC,且AD>BC,BC= 6cm, AD=9cm, P、Q分别从A、C同时出发,P以1cm/s的速度由A向D运动,Q以2cm/s的速度由C向B运动,多少s时直线将四边形ABCD截出一个平行四边形( )
A.1 B.2 C.3 D.2或3
二、填空题
16.若是不在同一条直线的三点,则以这三点为顶点画平行四边形,可画_____个.
17.在四边形ABCD中,AB=CD,请添加一个条件_____,使得四边形ABCD是平行四边形.
18.如图,在平行四边形中,相交于点O,点E,F在对角线上,有下列条件:①;②;③;④.其中一定能判定四边形是平行四边形的是______.
19.如图,在等腰梯形 ABCD 中,AD∥BC,AB=CD.点 P 为底边 BC 的延长线上任意一点,PE⊥AB 于 E,PF⊥DC 于 F,BM⊥DC 于 M.请你探究线段 PE、PF、BM 之间的数量关系:
______.
20.已知:一组邻边分别为和的平行四边形,和的平分线分别交所在直线于点,,则线段的长为________.
三、解答题
21.如图,已知四边形,请在下列三个关系中,选出两个恰当的关系作为条件,推出四边形是平行四边形,并予以证明.
关系:①,②, ③
已知:在四边形中, , ;(填序号,写出一种情况即可)
求证:四边形是平行四边形.
22.如图,在四边形ABCD中,,厘米,厘米,点P,Q分别从点A,C同时出发,点P以1厘米/秒的速度由点A向点D运动,点Q以2厘米/秒的速度由点C向点B运动.当一点到达终点时,两点均停止运动.
(1)经过几秒四边形ABQP为平行四边形
(2)经过几秒直线PQ将四边形ABCD截出一个平行四边形
23.如图,四边形中,,是边的中点,连接并延长与的延长线相交于点.
(1)求证:四边形是平行四边形;
(2)若,,.直接写出四边形的周长______.
24.在中,,点为所在平面内一点,过点分别作交于点,交于点,交于点.
(1)如图1,当点在边上时,请探索线段,,之间的数量关系,并证明你的结论.
(2)如图2,当点在内部时,线段,,,之间有怎样的数量关系?请说明理由.
(3)如图3,当点在外部时,线段,,,之间有怎样的数量关系?直接写出结论.
25.如图,中,,连结,是边上一点,连结交于点.
(1)如图1,连结,若,,求的面积;
(2)如图2,延长至点,连结、,点在上,且,,过作于点.若,求证:
参考答案:
1--10DDDCC CCDCD 11---15ACCBD
16.
17.AB//CD等
18.①④
19.PE-PF=BM.
20.或
21.(1)解:选择:①,③,
证明:∵∠B+∠C=180°, ∴AB∥DC,
又∵AD∥BC,
∴四边形ABCD是平行四边形;
故答案为:AD∥BC,∠A=∠C.
22.解:(1)设经过t秒四边形ABQP是平行四边形,
根据题意,得AP=t厘米,CQ=2t厘米,
则BQ=(6-2t)厘米,
∵AD∥BC,
∴当AP=BQ时,四边形ABQP是平行四边形,
∴t=6-2t,
解得t=2,
即经过2秒四边形ABQP为平行四边形;
(2)由(1)知,经过2秒四边形ABQP是平行四边形,设经过x秒直线PQ将四边形ABCD截出另一个平行四边形DCQP,
根据题意,得AP=x厘米,CQ=2x厘米,
则PD=(9-x)厘米,
∵AD∥BC,
∴当CQ=PD时,四边形DCQP是平行四边形,
∴2x=9-x,
解得x=3.
综上,经过2秒或3秒直线PQ将四边形ABCD截出一个平行四边形.
23.(1)证明:∵∠A=∠ABC=90°,
∴BC∥AD,
∴∠CBE=∠DFE,
在△BEC与△FED中,
,
∴△BEC≌△FED,
∴BE=FE,
又∵E是边CD的中点,
∴CE=DE,
∴四边形BDFC是平行四边形;
(2)∵BF⊥CD,四边形BDFC是平行四边形,
∴四边形BDFC是菱形,
∵AD=10cm,AF=30cm,
∴DF=30-10=20cm,
∴BD=BC=CF=DF=20cm,
∵在Rt△BAD中,
AB=cm,
∴四边形ABCF的周长是30+20×2+=70+(cm).
故四边形ABCF的周长是(70+)cm.
24.解:(1)PE+PF=AB.
证明:∵,
∴四边形FPEA为平行四边形
∴PF=AE,PE=AF
∵
∴∠EPB=∠C
∵AB=AC
∴∠B=∠C
∴∠EPB=∠B
∴BF=FP
∴AB=AF+FB=PE+FB=PE+FP=PE+AE
∴PE+PF=AB.
(2).
证明:∵,
∴四边形FPEA为平行四边形
∴PF=AE,PE=AF
∵
∴∠B=∠EDC
∵∠B=∠C
∴∠EDC=∠C
∴ED=EC
∴AB=AC=AE+EC=FP+ED=PF+PD+PE
∴.
(3).
证明:∵,
∴四边形FPEA为平行四边形
∴PF=AE,PE=AF
∵
∴∠B=∠EDC
∵∠B=∠C
∴∠EDC=∠C
∴ED=EC
∴AB=AC=AE+EC=PF+ED=PF+PE-PD
∴.
25.解:(1)
如图:过A点作AN⊥BE,交BE于N.
∵,
∴△ABE为等边三角形,
∴AB=BE=AE=6
即:AN=
∵
∴
∵BE=6
∴BC=10
∴EC=4
∴
即:的面积为.
(2)
如图:延长GD至P使DP=BG,连接AP,
∵AH=AF,
∴∠AFH=∠AHF
即:∠AFB=∠AHD,
又∵AF=AH,BF=DH,
∴≌
∴AB=AD
又∵,,
∴∠ABG=∠ADP
∵BG=DP,
∴≌
∴AG=AP,∠BAG=∠DAP
∵∠ABC=60°
∴∠BAD=120°
即:∠GAP=120°
∴∠AGP=∠APG=60°,
又∵AM⊥GD
∴GP=2GM=AG,
∵BG=GP
∴BG+GD=GD+DP=GP
即:BG+GD=AG.
