7.6 章末复习提升课 第七章 随机变量及其分布 人教A版选择性必修第三册 学案
文档属性
| 名称 | 7.6 章末复习提升课 第七章 随机变量及其分布 人教A版选择性必修第三册 学案 | 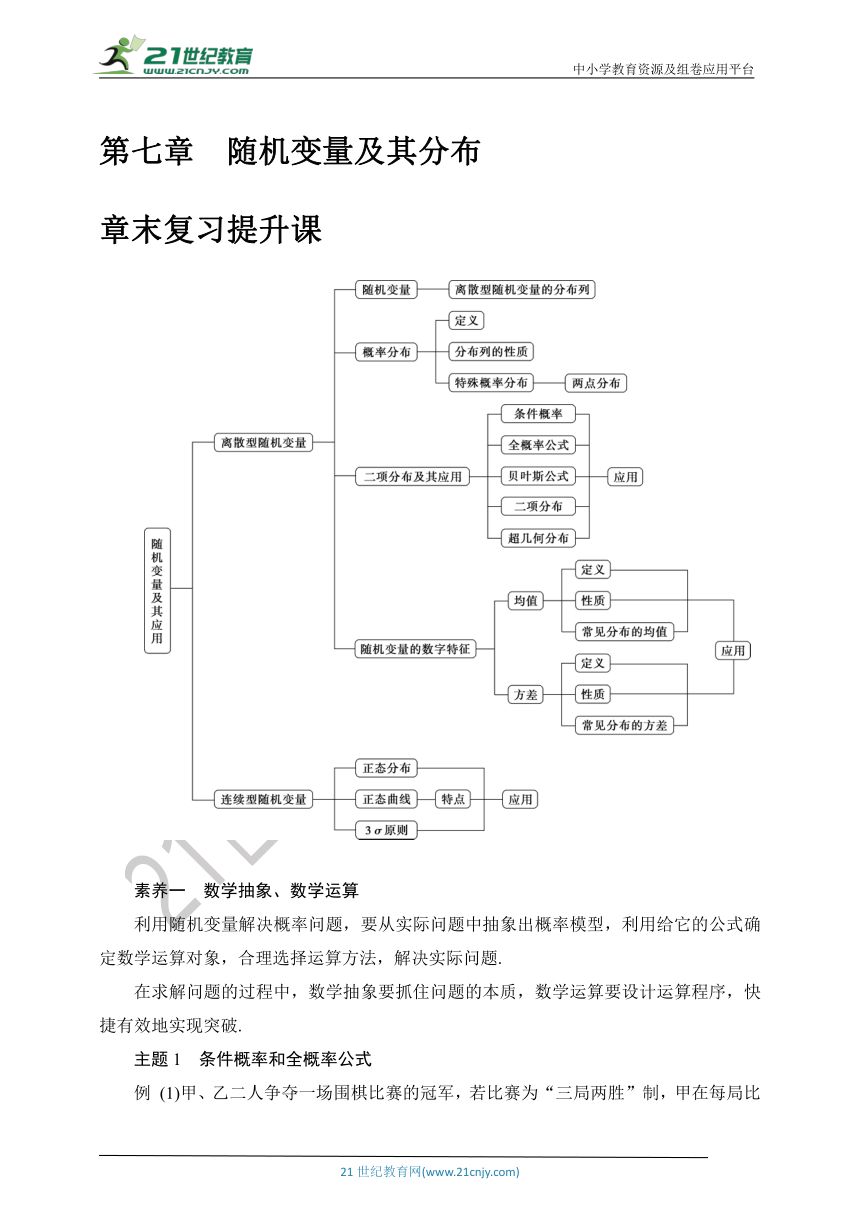 | |
| 格式 | doc | ||
| 文件大小 | 519.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-21 08:22:11 | ||
图片预览





文档简介
中小学教育资源及组卷应用平台
第七章 随机变量及其分布
章末复习提升课
素养一 数学抽象、数学运算
利用随机变量解决概率问题,要从实际问题中抽象出概率模型,利用给它的公式确定数学运算对象,合理选择运算方法,解决实际问题.
在求解问题的过程中,数学抽象要抓住问题的本质,数学运算要设计运算程序,快捷有效地实现突破.
主题1 条件概率和全概率公式
例 (1)甲、乙二人争夺一场围棋比赛的冠军,若比赛为“三局两胜”制,甲在每局比赛中获胜的概率均为,且各局比赛结果相互独立.则在甲获得冠军的情况下,比赛进行了三局的概率为( )
A. B.
C. D.
(2)在A,B,C三个地区爆发了流感,这三个地区分别有6%,5%,4%的人患了流感.假设这三个地区人口数的比为5∶7∶8,现从这三个地区中任意选取一个人.则这个人患流感的概率为 .
【解析】 (1)记事件A:“甲获得冠军”,事件B:“比赛进行三局”,事件AB:“甲获得冠军,且比赛进行了三局”,则第三局甲胜,前三局甲胜了两局,由独立事件的概率乘法公式得P(AB)=C×××=,对于事件A,甲获得冠军,包含两种情况:前两局甲胜和事件AB,所以P(A)=+=,所以P(B|A)==×=.
(2)设事件D为“这个人患流感”,A1,A2,A3分别表示这个人选自A,B,C地区.
由已知得P(A1)=0.25,P(A2)=0.35,
P(A3)=0.4,P(D|A1)=0.06,P(D|A2)=0.05,P(D|A3)=0.04.
由全概率公式,得P(D)=P(A1)P(D|A1)+P(A2)P(D|A2)+P(A3)P(D|A3)=0.06×0.25+0.05×0.35+0.04×0.4=0.048 5.
【答案】 (1)A (2)0.048 5
(1)条件概率计算的两种方法:定义法、缩小样本空间法.
(2)全概率公式针对的是随机试验第一阶段的各试验结果未知,求第二阶段某一结果发生的概率.
设某工厂有两个车间生产同种型号的家用电器,一车间的次品率为0.15,二车间的次品率为0.12,两个车间的成品都混合堆放在一个仓库.假设一、二车间生产的成品数量比例为2∶3,现有一客户从成品仓库中随机提一台产品,求该产品的合格的概率.
解:设“提出的一台产品是合格品”为事件B,“提出的一台产品是第i车间生产的”为事件Ai,i=1,2,则Ω=A1∪A2,且A1,A2互斥,则B=A1B∪A2B.由题意得P(A1)=0.4,P(A2)=0.6,P(B|A1)=0.85,P(B|A2)=0.88,由全概率公式得P(B)=P(A1)P(B|A1)+P(A2)P(B|A2)=0.4×0.85+0.6×0.88=0.868.
主题2 二项分布
例 某学校为了丰富学生的业余生活,以班级为单位组织学生开展古诗词背诵比赛,随机抽取题目,背诵正确加10分,背诵错误减10分,只有“正确”和“错误”两种结果.其中某班背诵正确的概率为p=,背诵错误的概率为q=,现记“该班完成n首背诵后总得分为Sn”.
(1)求S6=20且Si≥0(i=1,2,3)的概率;
(2)记X=|S5|,求X的数学期望及方差(保留小数点后两位有效数字).
【解】 (1)当S6=20时,即背诵6首后,4首正确,2首错误,
若第1首和第2首背诵正确,则其余4首可任意背诵2首正确;
若第1首背诵正确,第2首背诵错误,第3首背诵正确,其余3首可任意背诵2首正确,故所求的概率为
P=()2×C×()2×()2+×××C×()2×=.
(2)因为X=|S5|的取值为10,30,50.又p=,q=,
所以P(X=10)=C×()3×()2+C×()2×()3=,
P(X=30)=C×()4×+C××()4=,
P(X=50)=C×()5+C×()5=.
所以X的分布列为
X 10 30 50
P
所以E(X)=10×+30×+50×=≈22.84,D(X)=×(10-)2+×(30-)2+×(50-)2≈200.58.
二项分布实际上是对n重伯努利试验从概率分布的角度作了进一步阐述,与n重伯努利试验恰有k次发生的概率对应.
已知某种从太空飞船中带回来的植被种子每粒成功发芽的概率都为,某植物研究所分两个小组分别独立开展该种子的发芽试验,每次试验种一粒种子,如果某次没有发芽,则称该次试验是失败的.
(1)第一小组做了3次试验,记该小组试验成功的次数为X,求X的分布列;
(2)第二小组进行试验,到成功了4次为止,求在第4次成功之前共有3次失败的概率.
解:(1)由题意得,随机变量X可能的取值为0,1,2,3,则X~B.即P(X=0)=C=,P(X=1) =C=,P(X=2)=C =,P(X=3)=C=.
所以X的分布列为
X 0 1 2 3
P
(2)由题意可知,第二小组第7次试验成功,前面6次试验中有3次失败,3次成功,每次试验又是相互独立的,因此所求概率为P=C××=.
主题3 超几何分布与二项分布的综合应用
例 在10件产品中有2件次品,连续抽取3次,每次抽取1件,求:
(1)不放回抽样时,抽取次品数ξ的均值;
(2)放回抽样时,抽取次品数η的均值.
【解】 (1)方法一:由题知ξ的可能取值为0,1,2,则P(ξ=0)=eq \f(C,C)=,P(ξ=1)=eq \f(CC,C)=,P(ξ=2)=eq \f(CC,C)=,所以随机变量ξ的分布列为
ξ 0 1 2
P
E(ξ)=0×+1×+2×=.
方法二:由题意知P(ξ=k)=eq \f(CC,C)(k=0,1,2),
所以随机变量ξ服从超几何分布,n=3,M=2,N=10,
所以E(ξ)===.
(2)由题意知抽取1次取到次品的概率为=,
则随机变量η服从二项分布B,
所以E(η)=3×=.
由伯努利试验得出二项分布,由古典概型得出超几何分布,这两个分布的关系:若采用有放回抽样,则随机变量服从二项分布,若采用不放回抽样,则随机变量服从超几何分布.
1.(多选)(2021·山东潍坊昌乐二中2020高二月考)一袋中有大小相同的4个红球和2个白球,下列结论中正确的有( )
A.从中任取3个球,恰有1个白球的概率为
B.从中有放回地取球6次,每次任取一球,恰好有两次取到白球的概率为
C.现从中不放回地取球2次,每次任取一球,则在第一次取到红球后,第二次再次取到红球的概率为
D.从中有放回地取球3次,每次任取一球,则至少有一次取到红球的概率为
解析:选ABD.一袋中有大小相同的4个红球和2个白球.从中任取3个球,恰有1个白球的概率为eq \f(CC,C)=,故A正确;从中有放回地取球6次,每次任取一球,每次取到白球的概率为=,则恰好有两次取到白球的概率为C×=,故B正确;设事件A为“第一次取到红球”,事件B为“第二次取到红球”,则P(A)==,P(AB)=eq \f(CC,CC)=,则P(B|A)==,故C错误;从中有放回地取球3次,每次任取一球,每次取到红球的概率为=,则至少有一次取到红球的概率为1-C=,故D正确.故选ABD.
2.(2021·浙江舟山高三期末)一个口袋里装有大小相同的5个小球,其中红色2个,其余3个颜色各不相同.现从中任意取出3个小球,其中恰有2个小球颜色相同的概率是 ;若变量X为取出的3个小球中红球的个数,则X的数学期望E(X)= .
解析:一个口袋里装有大小相同的5个小球,其中红色2个,其余3个颜色各不相同.现从中任意取出3个小球,样本点总数n=C=10,其中恰有2个小球颜色相同包含的样本点个数m=CC=3,所以其中恰有2个小球颜色相同的概率是P==.若变量X为取出的3个小球中红球的个数,则X的可取值为0,1,2,P(X=0)=eq \f(C,C)=,P(X=1)=eq \f(CC,C)=,P(X=2)=eq \f(CC,C)=,则E(X)=0×+1×+2×=.
答案:
素养二 逻辑推理与数据分析
根据随机变量的特征,寻找并计算随机变量的方差、均值,理解随机变量、概率、分布列之间的逻辑关系,体现了逻辑推理的数学素养.
用随机变量刻画随机现象,用概率或统计模型解决实际问题,体现了数据分析的素养.
主题4 随机变量的均值、方差
例 同时投掷两枚相同的正方体骰子(骰子质地均匀,且各面分别刻有数字1,2,2,3,3,3).
(1)设随机变量η表示一次掷得的点数和,求η的分布列;
(2)若连续投掷10次,设随机变量ξ表示一次掷得的点数和大于5的次数,求E(ξ),D(ξ).
【解】 (1)由已知,随机变量η的取值为2,3,4,5,6.
投掷一次正方体骰子所得点数为X,则
P(X=1)=,P(X=2)=,P(X=3)=,
即P(η=2)=×=,
P(η=3)=2××=,
P(η=4)=2××+×=,
P(η=5)=2××=,
P(η=6)=×=.
故η的分布列为
P 2 3 4 5 6
η
(2)由已知,满足条件的一次投掷的点数和取值为6,设其发生的概率为p,由(1)知,p=,
因为随机变量ξ~B,
所以E(ξ)=np=10×=,
D(ξ)=np(1-p)=10××=.
求离散型随机变量的期望与方差的步骤
一项试验有两套方案,每套方案试验成功的概率都是,试验不成功的概率都是,甲随机地从两套方案中选取一套进行这项试验,共试验了3次,每次试验相互独立,且要从两套方案中等可能地选择一套.
(1)求3次试验都选择了同一套方案且都试验成功的概率;
(2)记“3次试验中,都选择了第一套方案并试验成功的次数”为X,求X的分布列和期望E(X).
解:记事件“一次试验中,选择第i套方案并试验成功”为Ai,i=1,2,则P=eq \f(1,C)×=.
(1)3次试验选择了同一套方案且都试验成功的概率为
P=P=3+3=.
(2)X的可能值为0,1,2,3,则X~B,
P=C,k=0,1,2,3,
X的分布列为
X 0 1 2 3
P
E(X)=3×=1.
主题5 正态分布
例 (1)设随机变量ξ服从正态分布N(4,3),若P(ξa+1),则实数a=( )
A.7 B.6
C.5 D.4
(2)已知随机变量X服从正态分布N(1,σ2),若P(X>2)=0.15,则P(0≤X≤1)=( )
A.0.85 B.0.70
C.0.35 D.0.15
【解析】 (1)由随机变量ξ服从正态分布N(4,3)可得正态密度曲线的对称轴为直线x=4,又P(ξa+1),所以x=a-5与x=a+1关于直线x=4对称,所以(a-5)+(a+1)=8,即a=6.故选B.
(2)P(0≤X≤1)=P(1≤X≤2)=0.5-P(X>2)=0.35.
【答案】 (1)B (2)C
根据正态曲线的对称性求解概率的三个关键点
(1)正态曲线与x轴之间的图形的面积为1.
(2)正态曲线关于直线x=μ对称,则正态曲线在对称轴x=μ的左右两侧与x轴围成的面积都为0.5.
(3)可以利用等式P(X≥μ+c)=P(X≤μ-c)(c>0)对目标概率进行转化求解.
在如图所示的正方形区域中随机投掷10 000个豆子,则落入阴影部分(曲线C为正态分布N(-1,1)的密度曲线)的豆子的个数的估计值为( )
(参考数据:若X~N(μ,σ2),则P(μ-σ≤X≤μ+σ)≈0.682 7,P(μ-2σ≤X≤μ+2σ)≈0.954 5,P(μ-3σ≤X≤μ+3σ)≈0.997 3)
A.1 193 B.1 359
C.2 718 D.3 413
解析:选B.对于正态分布N(-1,1),μ=-1,σ=1,正态曲线关于直线x=-1对称,故题图中阴影部分的面积约为×(0.954 5-0.682 7)=0.135 9,所以豆子落入题图中阴影部分的概率为P==0.135 9,所以投入10 000个豆子,落入阴影部分的个数约为10 000×0.135 9=1 359.
主题6 决策问题
例 某煤矿发生透水事故时,作业区有若干人员被困.救援队从入口进入后,有L1,L2两条巷道通往作业区(如图).L1巷道有A1,A2,A3三个易堵塞点,各点被堵塞的概率都是;L2巷道有B1,B2两个易堵塞点,被堵塞的概率分别为,.
(1)求L1巷道中,三个易堵塞点最多有一个被堵塞的概率;
(2)若L2巷道堵塞点的个数为X,求X的分布列及数学期望E(X),并请你按照“平均堵塞点少的巷道是较好的抢险路线”的标准,帮助救援队选择一条抢险路线,同时说明理由.
【解】 (1)设事件A=“L1巷道中,三个易堵塞点最多有一个被堵塞”,则P(A)=C×+C××=.
(2)根据题意,知X的可能取值为0,1,2.
P(X=0)=×=,
P(X=1)=×+×=.
P(X=2)=×=.
所以随机变量X的分布列为
X 0 1 2
P
E(X)=0×+1×+2×=.
方法一:设L1巷道中堵塞点个数为Y,则Y的可能取值为0,1,2,3.
P(Y=0)=C×=,
P(Y=1)=C××=,
P(Y=2)=C××=,
P(Y=3)=C×=.
所以随机变量Y的分布列为
Y 0 1 2 3
P
E(Y)=0×+1×+2×+3×=.
因为E(X)方法二:设L1巷道中堵塞点个数为Y,则随机变量Y~B,所以E(Y)=3×=.
因为E(X)利用随机变量的分布特征计算随机变量的均值、方差,根据实际意义可以对决策问题提供依据.
某联欢晚会举行抽奖活动,举办方设置了甲、乙两种抽奖方案,方案甲的中奖率为,中奖可以获得2分;方案乙的中奖率为,中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.
(1)若小明选择方案甲抽奖,小红选择方案乙抽奖,记他们的累计得分为X,求X≤3的概率;
(2)若小明、小红两人都选择方案甲或都选择方案乙进行抽奖,问:他们选择何种方案抽奖,累计得分的数学期望较大?
解:(1)由已知得,小明中奖的概率为,小红中奖的概率为,且两人中奖与否互不影响,记“这2人的累计得分X≤3”的事件为A,则事件A的对立事件为“X=5”,因为P(X=5)=×=,所以P(A)=1-P(X=5)=,所以这两人的累计得分X≤3的概率为.
(2)方法一:设小明、小红都选择方案甲抽奖中奖的次数为X1,都选择方案乙抽奖中奖的次数为X2,则这两人选择方案甲抽奖累计得分的数学期望为E(2X1),选择方案乙抽奖累计得分的数学期望为E(3X2).由已知:X1~B,X2~B,所以E(X1)=2×=,E(X2)=2×=,因此E(2X1)=2E(X1)=,E(3X2)=3E(X2)=.因为E(2X1)>E(3X2),所以他们都选择方案甲进行抽奖时,累计得分的数学期望较大.
方法二:设小明、小红都选择方案甲所获得的累计得分为Y1,都选择方案乙所获得的累计得分为Y2,则Y1,Y2的分布列为
Y1 0 2 4
P
Y2 0 3 6
P
所以E(Y1)=0×+2×+4×=,E(Y2)=0×+3×+6×=,因为E(Y1)>E(Y2),所以二人都选择方案甲抽奖,累计得分的数学期望较大.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
第七章 随机变量及其分布
章末复习提升课
素养一 数学抽象、数学运算
利用随机变量解决概率问题,要从实际问题中抽象出概率模型,利用给它的公式确定数学运算对象,合理选择运算方法,解决实际问题.
在求解问题的过程中,数学抽象要抓住问题的本质,数学运算要设计运算程序,快捷有效地实现突破.
主题1 条件概率和全概率公式
例 (1)甲、乙二人争夺一场围棋比赛的冠军,若比赛为“三局两胜”制,甲在每局比赛中获胜的概率均为,且各局比赛结果相互独立.则在甲获得冠军的情况下,比赛进行了三局的概率为( )
A. B.
C. D.
(2)在A,B,C三个地区爆发了流感,这三个地区分别有6%,5%,4%的人患了流感.假设这三个地区人口数的比为5∶7∶8,现从这三个地区中任意选取一个人.则这个人患流感的概率为 .
【解析】 (1)记事件A:“甲获得冠军”,事件B:“比赛进行三局”,事件AB:“甲获得冠军,且比赛进行了三局”,则第三局甲胜,前三局甲胜了两局,由独立事件的概率乘法公式得P(AB)=C×××=,对于事件A,甲获得冠军,包含两种情况:前两局甲胜和事件AB,所以P(A)=+=,所以P(B|A)==×=.
(2)设事件D为“这个人患流感”,A1,A2,A3分别表示这个人选自A,B,C地区.
由已知得P(A1)=0.25,P(A2)=0.35,
P(A3)=0.4,P(D|A1)=0.06,P(D|A2)=0.05,P(D|A3)=0.04.
由全概率公式,得P(D)=P(A1)P(D|A1)+P(A2)P(D|A2)+P(A3)P(D|A3)=0.06×0.25+0.05×0.35+0.04×0.4=0.048 5.
【答案】 (1)A (2)0.048 5
(1)条件概率计算的两种方法:定义法、缩小样本空间法.
(2)全概率公式针对的是随机试验第一阶段的各试验结果未知,求第二阶段某一结果发生的概率.
设某工厂有两个车间生产同种型号的家用电器,一车间的次品率为0.15,二车间的次品率为0.12,两个车间的成品都混合堆放在一个仓库.假设一、二车间生产的成品数量比例为2∶3,现有一客户从成品仓库中随机提一台产品,求该产品的合格的概率.
解:设“提出的一台产品是合格品”为事件B,“提出的一台产品是第i车间生产的”为事件Ai,i=1,2,则Ω=A1∪A2,且A1,A2互斥,则B=A1B∪A2B.由题意得P(A1)=0.4,P(A2)=0.6,P(B|A1)=0.85,P(B|A2)=0.88,由全概率公式得P(B)=P(A1)P(B|A1)+P(A2)P(B|A2)=0.4×0.85+0.6×0.88=0.868.
主题2 二项分布
例 某学校为了丰富学生的业余生活,以班级为单位组织学生开展古诗词背诵比赛,随机抽取题目,背诵正确加10分,背诵错误减10分,只有“正确”和“错误”两种结果.其中某班背诵正确的概率为p=,背诵错误的概率为q=,现记“该班完成n首背诵后总得分为Sn”.
(1)求S6=20且Si≥0(i=1,2,3)的概率;
(2)记X=|S5|,求X的数学期望及方差(保留小数点后两位有效数字).
【解】 (1)当S6=20时,即背诵6首后,4首正确,2首错误,
若第1首和第2首背诵正确,则其余4首可任意背诵2首正确;
若第1首背诵正确,第2首背诵错误,第3首背诵正确,其余3首可任意背诵2首正确,故所求的概率为
P=()2×C×()2×()2+×××C×()2×=.
(2)因为X=|S5|的取值为10,30,50.又p=,q=,
所以P(X=10)=C×()3×()2+C×()2×()3=,
P(X=30)=C×()4×+C××()4=,
P(X=50)=C×()5+C×()5=.
所以X的分布列为
X 10 30 50
P
所以E(X)=10×+30×+50×=≈22.84,D(X)=×(10-)2+×(30-)2+×(50-)2≈200.58.
二项分布实际上是对n重伯努利试验从概率分布的角度作了进一步阐述,与n重伯努利试验恰有k次发生的概率对应.
已知某种从太空飞船中带回来的植被种子每粒成功发芽的概率都为,某植物研究所分两个小组分别独立开展该种子的发芽试验,每次试验种一粒种子,如果某次没有发芽,则称该次试验是失败的.
(1)第一小组做了3次试验,记该小组试验成功的次数为X,求X的分布列;
(2)第二小组进行试验,到成功了4次为止,求在第4次成功之前共有3次失败的概率.
解:(1)由题意得,随机变量X可能的取值为0,1,2,3,则X~B.即P(X=0)=C=,P(X=1) =C=,P(X=2)=C =,P(X=3)=C=.
所以X的分布列为
X 0 1 2 3
P
(2)由题意可知,第二小组第7次试验成功,前面6次试验中有3次失败,3次成功,每次试验又是相互独立的,因此所求概率为P=C××=.
主题3 超几何分布与二项分布的综合应用
例 在10件产品中有2件次品,连续抽取3次,每次抽取1件,求:
(1)不放回抽样时,抽取次品数ξ的均值;
(2)放回抽样时,抽取次品数η的均值.
【解】 (1)方法一:由题知ξ的可能取值为0,1,2,则P(ξ=0)=eq \f(C,C)=,P(ξ=1)=eq \f(CC,C)=,P(ξ=2)=eq \f(CC,C)=,所以随机变量ξ的分布列为
ξ 0 1 2
P
E(ξ)=0×+1×+2×=.
方法二:由题意知P(ξ=k)=eq \f(CC,C)(k=0,1,2),
所以随机变量ξ服从超几何分布,n=3,M=2,N=10,
所以E(ξ)===.
(2)由题意知抽取1次取到次品的概率为=,
则随机变量η服从二项分布B,
所以E(η)=3×=.
由伯努利试验得出二项分布,由古典概型得出超几何分布,这两个分布的关系:若采用有放回抽样,则随机变量服从二项分布,若采用不放回抽样,则随机变量服从超几何分布.
1.(多选)(2021·山东潍坊昌乐二中2020高二月考)一袋中有大小相同的4个红球和2个白球,下列结论中正确的有( )
A.从中任取3个球,恰有1个白球的概率为
B.从中有放回地取球6次,每次任取一球,恰好有两次取到白球的概率为
C.现从中不放回地取球2次,每次任取一球,则在第一次取到红球后,第二次再次取到红球的概率为
D.从中有放回地取球3次,每次任取一球,则至少有一次取到红球的概率为
解析:选ABD.一袋中有大小相同的4个红球和2个白球.从中任取3个球,恰有1个白球的概率为eq \f(CC,C)=,故A正确;从中有放回地取球6次,每次任取一球,每次取到白球的概率为=,则恰好有两次取到白球的概率为C×=,故B正确;设事件A为“第一次取到红球”,事件B为“第二次取到红球”,则P(A)==,P(AB)=eq \f(CC,CC)=,则P(B|A)==,故C错误;从中有放回地取球3次,每次任取一球,每次取到红球的概率为=,则至少有一次取到红球的概率为1-C=,故D正确.故选ABD.
2.(2021·浙江舟山高三期末)一个口袋里装有大小相同的5个小球,其中红色2个,其余3个颜色各不相同.现从中任意取出3个小球,其中恰有2个小球颜色相同的概率是 ;若变量X为取出的3个小球中红球的个数,则X的数学期望E(X)= .
解析:一个口袋里装有大小相同的5个小球,其中红色2个,其余3个颜色各不相同.现从中任意取出3个小球,样本点总数n=C=10,其中恰有2个小球颜色相同包含的样本点个数m=CC=3,所以其中恰有2个小球颜色相同的概率是P==.若变量X为取出的3个小球中红球的个数,则X的可取值为0,1,2,P(X=0)=eq \f(C,C)=,P(X=1)=eq \f(CC,C)=,P(X=2)=eq \f(CC,C)=,则E(X)=0×+1×+2×=.
答案:
素养二 逻辑推理与数据分析
根据随机变量的特征,寻找并计算随机变量的方差、均值,理解随机变量、概率、分布列之间的逻辑关系,体现了逻辑推理的数学素养.
用随机变量刻画随机现象,用概率或统计模型解决实际问题,体现了数据分析的素养.
主题4 随机变量的均值、方差
例 同时投掷两枚相同的正方体骰子(骰子质地均匀,且各面分别刻有数字1,2,2,3,3,3).
(1)设随机变量η表示一次掷得的点数和,求η的分布列;
(2)若连续投掷10次,设随机变量ξ表示一次掷得的点数和大于5的次数,求E(ξ),D(ξ).
【解】 (1)由已知,随机变量η的取值为2,3,4,5,6.
投掷一次正方体骰子所得点数为X,则
P(X=1)=,P(X=2)=,P(X=3)=,
即P(η=2)=×=,
P(η=3)=2××=,
P(η=4)=2××+×=,
P(η=5)=2××=,
P(η=6)=×=.
故η的分布列为
P 2 3 4 5 6
η
(2)由已知,满足条件的一次投掷的点数和取值为6,设其发生的概率为p,由(1)知,p=,
因为随机变量ξ~B,
所以E(ξ)=np=10×=,
D(ξ)=np(1-p)=10××=.
求离散型随机变量的期望与方差的步骤
一项试验有两套方案,每套方案试验成功的概率都是,试验不成功的概率都是,甲随机地从两套方案中选取一套进行这项试验,共试验了3次,每次试验相互独立,且要从两套方案中等可能地选择一套.
(1)求3次试验都选择了同一套方案且都试验成功的概率;
(2)记“3次试验中,都选择了第一套方案并试验成功的次数”为X,求X的分布列和期望E(X).
解:记事件“一次试验中,选择第i套方案并试验成功”为Ai,i=1,2,则P=eq \f(1,C)×=.
(1)3次试验选择了同一套方案且都试验成功的概率为
P=P=3+3=.
(2)X的可能值为0,1,2,3,则X~B,
P=C,k=0,1,2,3,
X的分布列为
X 0 1 2 3
P
E(X)=3×=1.
主题5 正态分布
例 (1)设随机变量ξ服从正态分布N(4,3),若P(ξ
A.7 B.6
C.5 D.4
(2)已知随机变量X服从正态分布N(1,σ2),若P(X>2)=0.15,则P(0≤X≤1)=( )
A.0.85 B.0.70
C.0.35 D.0.15
【解析】 (1)由随机变量ξ服从正态分布N(4,3)可得正态密度曲线的对称轴为直线x=4,又P(ξ
(2)P(0≤X≤1)=P(1≤X≤2)=0.5-P(X>2)=0.35.
【答案】 (1)B (2)C
根据正态曲线的对称性求解概率的三个关键点
(1)正态曲线与x轴之间的图形的面积为1.
(2)正态曲线关于直线x=μ对称,则正态曲线在对称轴x=μ的左右两侧与x轴围成的面积都为0.5.
(3)可以利用等式P(X≥μ+c)=P(X≤μ-c)(c>0)对目标概率进行转化求解.
在如图所示的正方形区域中随机投掷10 000个豆子,则落入阴影部分(曲线C为正态分布N(-1,1)的密度曲线)的豆子的个数的估计值为( )
(参考数据:若X~N(μ,σ2),则P(μ-σ≤X≤μ+σ)≈0.682 7,P(μ-2σ≤X≤μ+2σ)≈0.954 5,P(μ-3σ≤X≤μ+3σ)≈0.997 3)
A.1 193 B.1 359
C.2 718 D.3 413
解析:选B.对于正态分布N(-1,1),μ=-1,σ=1,正态曲线关于直线x=-1对称,故题图中阴影部分的面积约为×(0.954 5-0.682 7)=0.135 9,所以豆子落入题图中阴影部分的概率为P==0.135 9,所以投入10 000个豆子,落入阴影部分的个数约为10 000×0.135 9=1 359.
主题6 决策问题
例 某煤矿发生透水事故时,作业区有若干人员被困.救援队从入口进入后,有L1,L2两条巷道通往作业区(如图).L1巷道有A1,A2,A3三个易堵塞点,各点被堵塞的概率都是;L2巷道有B1,B2两个易堵塞点,被堵塞的概率分别为,.
(1)求L1巷道中,三个易堵塞点最多有一个被堵塞的概率;
(2)若L2巷道堵塞点的个数为X,求X的分布列及数学期望E(X),并请你按照“平均堵塞点少的巷道是较好的抢险路线”的标准,帮助救援队选择一条抢险路线,同时说明理由.
【解】 (1)设事件A=“L1巷道中,三个易堵塞点最多有一个被堵塞”,则P(A)=C×+C××=.
(2)根据题意,知X的可能取值为0,1,2.
P(X=0)=×=,
P(X=1)=×+×=.
P(X=2)=×=.
所以随机变量X的分布列为
X 0 1 2
P
E(X)=0×+1×+2×=.
方法一:设L1巷道中堵塞点个数为Y,则Y的可能取值为0,1,2,3.
P(Y=0)=C×=,
P(Y=1)=C××=,
P(Y=2)=C××=,
P(Y=3)=C×=.
所以随机变量Y的分布列为
Y 0 1 2 3
P
E(Y)=0×+1×+2×+3×=.
因为E(X)
因为E(X)
某联欢晚会举行抽奖活动,举办方设置了甲、乙两种抽奖方案,方案甲的中奖率为,中奖可以获得2分;方案乙的中奖率为,中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.
(1)若小明选择方案甲抽奖,小红选择方案乙抽奖,记他们的累计得分为X,求X≤3的概率;
(2)若小明、小红两人都选择方案甲或都选择方案乙进行抽奖,问:他们选择何种方案抽奖,累计得分的数学期望较大?
解:(1)由已知得,小明中奖的概率为,小红中奖的概率为,且两人中奖与否互不影响,记“这2人的累计得分X≤3”的事件为A,则事件A的对立事件为“X=5”,因为P(X=5)=×=,所以P(A)=1-P(X=5)=,所以这两人的累计得分X≤3的概率为.
(2)方法一:设小明、小红都选择方案甲抽奖中奖的次数为X1,都选择方案乙抽奖中奖的次数为X2,则这两人选择方案甲抽奖累计得分的数学期望为E(2X1),选择方案乙抽奖累计得分的数学期望为E(3X2).由已知:X1~B,X2~B,所以E(X1)=2×=,E(X2)=2×=,因此E(2X1)=2E(X1)=,E(3X2)=3E(X2)=.因为E(2X1)>E(3X2),所以他们都选择方案甲进行抽奖时,累计得分的数学期望较大.
方法二:设小明、小红都选择方案甲所获得的累计得分为Y1,都选择方案乙所获得的累计得分为Y2,则Y1,Y2的分布列为
Y1 0 2 4
P
Y2 0 3 6
P
所以E(Y1)=0×+2×+4×=,E(Y2)=0×+3×+6×=,因为E(Y1)>E(Y2),所以二人都选择方案甲抽奖,累计得分的数学期望较大.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
