2021-2022学年人教版九年级下册数学27.2.1相似三角形的判定同步测试(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级下册数学27.2.1相似三角形的判定同步测试(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 434.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-19 21:19:24 | ||
图片预览




文档简介
27.2.1相似三角形的判定 同步测试
一.选择题
1.把一张矩形的纸片对折后和原矩形相似,那么大矩形与小矩形的相似比是( )
A. :1 B. 4:1 C. 3:1 D. 2:1
2.下列图形中不一定是相似图形的是( )
A.两个等边三角形
B.两个顶角相等的等腰三角形
C.两个等腰直角三角形
D.两个矩形
3.下列图形中,任意两个图形一定是相似图形的是( )
A.三角形 B.平行四边形 C.抛物线 D.圆
4.用放大镜观察一个五边形时,不变的量是( )
A.各边的长度 B.各内角的度数
C.五边形的周长 D.五边形的面积
5.下列说法中,错误的是( )
A. 两个全等三角形一定是相似三角形
B. 两个等腰三角形一定相似
C. 两个等边三角形一定相似
D. 两个等腰直角三角形一定相似
6.已知一个三角形的两个内角分别是40°,60°,另一个三角形的两个内角分别是40°,80°,则这两个三角形( )
A. 一定不相似
B. 不一定相似
C. 一定相似
D. 不能确定
7.如图,在Rt△ABC中,∠C=90°,CD⊥AB,垂足为点D,一直角三角板的直角顶点与点D重合,这块三角板绕点D旋转,两条直角边始终与AC、BC边分别相交于G、H,则在运动过程中,△ADG与△CDH的关系是( )
A.一定相似 B.一定全等 C.不一定相似 D.无法判断
8.已知图(1)、(2)中各有两个三角形,其边长和角的度数已在图上标注,图(2)中AB、CD交于O点,对于各图中的两个三角形而言,下列说法正确的是( )
A. 只有(1)相似
B. 只有(2)相似
C. 都相似
D. 都不相似
9.如图,M是Rt△ABC的斜边BC上异于B、C的一定点,过M点作直线截△ABC,使截得的三角形与△ABC相似,这样的直线共有( )
A. 1条
B. 2条
C. 3条
D. 4条
10.如图,在钝角△ABC中,AB=5 cm,AC=10 cm,动点D从A点出发到B点止,动点E从C点出发到A点止,点D运动的速度为1 cm/秒,点E运动的速度为2 cm/秒,如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是( )
A. 2.5秒
B. 4.5秒
C. 2.5秒或4.5秒
D. 2.5秒或4秒
二.填空题
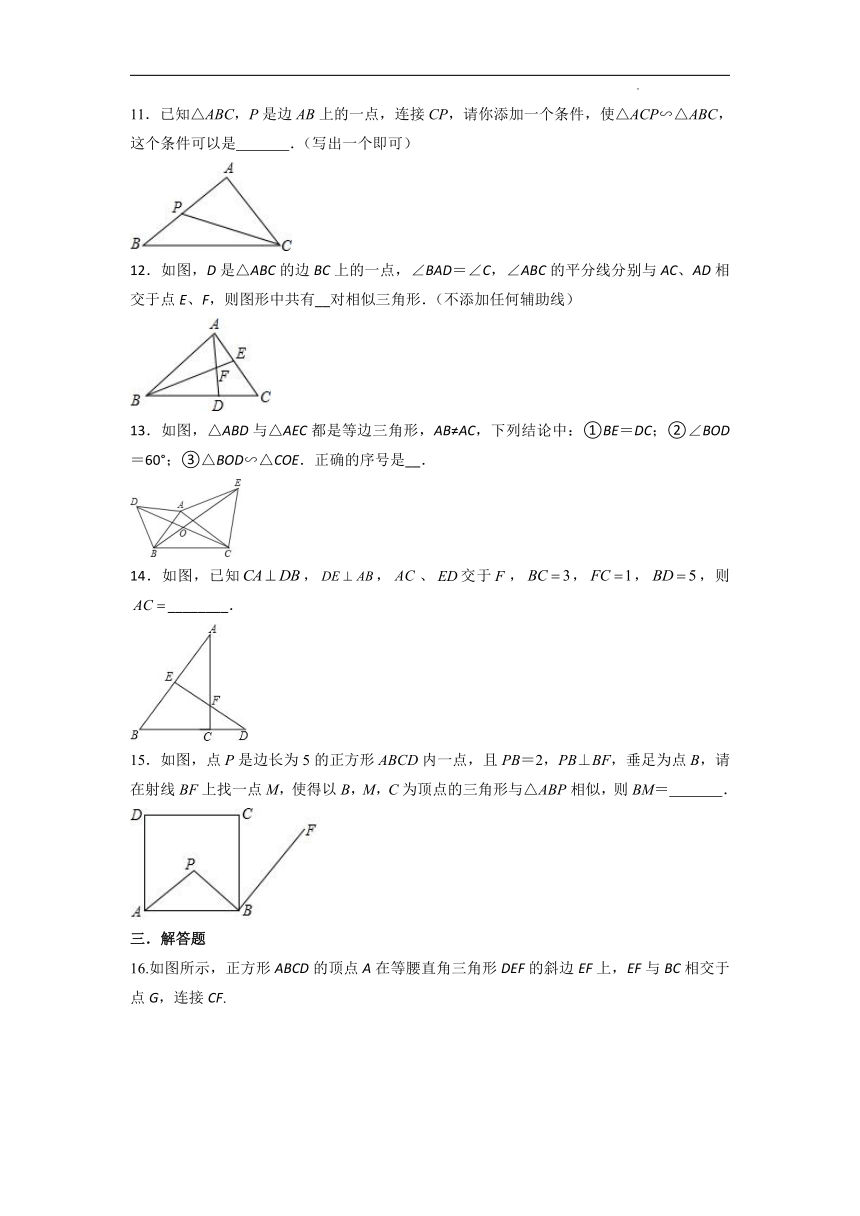
11.已知△ABC,P是边AB上的一点,连接CP,请你添加一个条件,使△ACP∽△ABC,这个条件可以是 .(写出一个即可)
12.如图,D是△ABC的边BC上的一点,∠BAD=∠C,∠ABC的平分线分别与AC、AD相交于点E、F,则图形中共有__对相似三角形.(不添加任何辅助线)
13.如图,△ABD与△AEC都是等边三角形,AB≠AC,下列结论中:①BE=DC;②∠BOD=60°;③△BOD∽△COE.正确的序号是__.
14.如图,已知,,、交于,,,,则________.
15.如图,点P是边长为5的正方形ABCD内一点,且PB=2,PB⊥BF,垂足为点B,请在射线BF上找一点M,使得以B,M,C为顶点的三角形与△ABP相似,则BM= .
三.解答题
16.如图所示,正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上,EF与BC相交于点G,连接CF.
(1)求证:△DAE≌△DCF;
(2)求证:△ABG∽△CFG.
17.如图所示,在等边中△ABC,D、E分别是AB、AC上的点,DE∥BC,如图(1),然后将△ADE绕A点顺时针旋转120°,使B、A、E三点在同一直线上,得到图(2),M、N分别是BD、CE的中点,连接AM、AN、MN得到图(3),请解答下列问题:
(1)在图(2)中,线段BD与线段CE的大小关系是____________;
(2)在图(3)中,△AMN与△ABC是相似三角形吗?请证明你的结论.
18.如图,点C为线段AB上任意一点(不与A、B两点重合),分别以AC、BC为一腰在AB的同侧作等腰△ACD和等腰△BCE,CA=CD,CB=CE,∠ACD与∠BCE都是锐角且∠ACD=∠BCE,连接AE交CD于点M,连接BD交CE于点N,AE与BD交于点P,连接PC.
(1)求证:△ACE≌△DCB;
(2)请你判断△AMC与△DPM的形状有何关系,并说明理由.
19.如图,在△ABC中,点D、E分别在边BC、AC上,连接AD、DE.且∠B=∠ADE=∠C.
(1)证明:△BDA∽△CED;
(2)若∠B=45°,BC=6,当点D在BC上运动时(点D不与B、C重合).且△ADE是等腰三角形,求此时BD的长.
20.如图,.
(1)求,,的值;
(2)证明与相似.
21.已知抛物线与轴分别交于两点,与轴交于点.
(1)求抛物线的表达式及顶点的坐标;
(2)点是线段上一个动点.
①如图1,设,当为何值时,有.
②如图2,若,求出点的坐标.
22.如图,是的外接圆,,延长到点,使得,连接交于点,过点做的平行线交于点.
(1)求证:;
(2)求证:为的切线;
(3)若,,求弦的长.
参考答案
1.A 2.A 3.C 4.B 5.C 6.A 7.A 8.C 9.C 10.D
11.∠ACP=∠B,或∠APC=∠ACB或=.
12.3
13.①②
14.6
15.2或.
16.【答案】证明 (1)∵四边形ABCD为正方形,△EDF为等腰直角三角形,
∴∠ADC=∠EDF=90°,AD=CD,DE=DF,
∴∠ADE+∠ADF=∠ADF+∠CDF,
∴∠ADE=∠CDF,
在△ADE和△CDF中,
∴△ADE≌△CDF;
(2)延长BA到M,交ED于点M,
∵△ADE≌△CDF,
∴∠EAD=∠FCD,即∠EAM+∠MAD=∠BCD+∠BCF,
∵∠MAD=∠BCD=90°,
∴∠EAM=∠BCF,
∵∠EAM=∠BAG,
∴∠BAG=∠BCF,
∵∠AGB=∠CGF,
∴△ABG∽△CFG.
【解析】(1)由正方形ABCD与等腰直角三角形DEF,得到两对边相等,一对直角相等,利用SAS即可得证;
(2)由第一问的全等三角形的对应角相等,根据等量代换得到∠BAG=∠BCF,再由对顶角相等,利用两对角相等的三角形相似即可得证.
17.【答案】解 (1)BD=CE;
理由:∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
在图(1)中,
∵DE∥BC,
∴△ADE∽△ABC,
∴△ADE是等边三角形,
∵△ADE绕A点顺时针旋转120°,使B、A、E三点在同一直线上,
∴如图(2),AD=AE,∠DAE=60°,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
∴△BAD≌△CAE(SAS),
∴BD=CE;
(2)△AMN与△ABC相似.
证明:∵M、N分别是BD、CE的中点,
∴EN=CE,DM=BD,
∵BD=CE,
∴EN=DM,
∵△BAD≌△CAE,
∴∠AEN=∠ADM,
在△ADM和△AEN中,
∴△ADM≌△AEN(SAS),
∴AM=AN,∠MAD=∠NAE,
∴∠MAN=∠DAE=60°,
∴△AMN也是等边三角形,
∴△AMN∽△ABC.
【解析】(1)由在等边中△ABC,DE∥BC,易证得△ADE也是等边三角形,然后利用SAS,证得△BAD≌△CAE,即可得BD=CE;
(2)由△BAD≌△CAE,可得∠AEN=∠ADM,又由M、N分别是BD、CE的中点,易得EN=DM,然后根据SAS证得△ADM≌△AEN,即可得AM=AN,∠MAN=60°,判定△AMN是等边三角形,即可得在图(3)中,△AMN与△ABC是相似三角形.
18.【答案】(1)证明 ∵∠ACD=∠BCE,
∴∠ACD+∠DCE=∠BCE+∠DCE,
∴∠ACE=∠DCB,
又∵CA=CD,CE=CB,
在△ACE和△DCB中,
∴△ACE≌△DCB(SAS).
(2)解 △AMC∽△DMP.
理由:∵△ACE≌△DCB,
∴∠CAE=∠CDB,
又∵∠AMC=∠DMP,
∴△AMC∽△DMP.
【解析】(1)证明∠ACE=∠DCB,根据“SAS”证明全等;
由(1)得∠CAM=∠PDM,又∠AMC=∠DMP,所以两个三角形相似.
19.【答案】解 (1)连接OA,
∵AB=AC,点A,B,C三点在⊙O上,
∴OA垂直平分BC,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴OA⊥AD,
∴AD是⊙O的切线;
(2)∵AB=AC,
∴∠DEA=∠BCA,
∵AD∥BC,
∴∠DAC=∠BCA,
∴∠DEA=∠DAC,
∵∠D=∠D,
∴△DAC∽△DEA.
【解析】(1)连接OA,根据AB=AC,点A,B,C三点在⊙O上,可得OA垂直平分BC,根据四边形ABCD是平行四边形,得OA⊥AD,即AD是⊙O的切线;
(2)根据AB=AC,∠DEA=∠BCA,再由AD∥BC,得∠DAC=∠BCA,从而得出∠DEA=∠DAC,可证△DAC∽△DEA.
20.【答案】解 乙同学的解答不正确,
与△ABC相似的三角形还有△GFE,应该补上证明如下:
∵DF∥BC,
∴∠GFE=∠ABC,
又∵∠E=∠C,
∴△GFE∽△ABC.
【解析】直接利用相似三角形判定定理得出△GFE∽△ABC即可.
21.解:抛物线过点,
解得:
抛物线解析式为;
顶点的坐标为;
在中,,
,
,
,
,
为直角三角形,且
为的中点,
在中,
在中,
连接 当时,,
设直线的解析式为
解得:
直线的解析式为
直线的解析式为
设直线的解析式为
解得:
直线的解析式为
解得:
22.(1)∵,
∴,
∵,
∴,
∴.
(2)如图,连接,
∵∠DBC=∠BDC,
∴∠ACB=2∠DBC,
∵∠DBC=∠EAC,
∴∠ACB=2∠EAC,
∵AB=BC,
∴∠BAC=∠ACB,
∴∠BAC=2∠EAC,
∴∠EAC=∠EAB,
∴点为的中点,
∴,
∵,
∴,
∴为圆的切线.
(3)在和中,,
∴,
∴,
∴,
∵AB=5,BE=3,
∴
∴,
由(1)得,
∵,
∴,
∵,
∴.
一.选择题
1.把一张矩形的纸片对折后和原矩形相似,那么大矩形与小矩形的相似比是( )
A. :1 B. 4:1 C. 3:1 D. 2:1
2.下列图形中不一定是相似图形的是( )
A.两个等边三角形
B.两个顶角相等的等腰三角形
C.两个等腰直角三角形
D.两个矩形
3.下列图形中,任意两个图形一定是相似图形的是( )
A.三角形 B.平行四边形 C.抛物线 D.圆
4.用放大镜观察一个五边形时,不变的量是( )
A.各边的长度 B.各内角的度数
C.五边形的周长 D.五边形的面积
5.下列说法中,错误的是( )
A. 两个全等三角形一定是相似三角形
B. 两个等腰三角形一定相似
C. 两个等边三角形一定相似
D. 两个等腰直角三角形一定相似
6.已知一个三角形的两个内角分别是40°,60°,另一个三角形的两个内角分别是40°,80°,则这两个三角形( )
A. 一定不相似
B. 不一定相似
C. 一定相似
D. 不能确定
7.如图,在Rt△ABC中,∠C=90°,CD⊥AB,垂足为点D,一直角三角板的直角顶点与点D重合,这块三角板绕点D旋转,两条直角边始终与AC、BC边分别相交于G、H,则在运动过程中,△ADG与△CDH的关系是( )
A.一定相似 B.一定全等 C.不一定相似 D.无法判断
8.已知图(1)、(2)中各有两个三角形,其边长和角的度数已在图上标注,图(2)中AB、CD交于O点,对于各图中的两个三角形而言,下列说法正确的是( )
A. 只有(1)相似
B. 只有(2)相似
C. 都相似
D. 都不相似
9.如图,M是Rt△ABC的斜边BC上异于B、C的一定点,过M点作直线截△ABC,使截得的三角形与△ABC相似,这样的直线共有( )
A. 1条
B. 2条
C. 3条
D. 4条
10.如图,在钝角△ABC中,AB=5 cm,AC=10 cm,动点D从A点出发到B点止,动点E从C点出发到A点止,点D运动的速度为1 cm/秒,点E运动的速度为2 cm/秒,如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是( )
A. 2.5秒
B. 4.5秒
C. 2.5秒或4.5秒
D. 2.5秒或4秒
二.填空题
11.已知△ABC,P是边AB上的一点,连接CP,请你添加一个条件,使△ACP∽△ABC,这个条件可以是 .(写出一个即可)
12.如图,D是△ABC的边BC上的一点,∠BAD=∠C,∠ABC的平分线分别与AC、AD相交于点E、F,则图形中共有__对相似三角形.(不添加任何辅助线)
13.如图,△ABD与△AEC都是等边三角形,AB≠AC,下列结论中:①BE=DC;②∠BOD=60°;③△BOD∽△COE.正确的序号是__.
14.如图,已知,,、交于,,,,则________.
15.如图,点P是边长为5的正方形ABCD内一点,且PB=2,PB⊥BF,垂足为点B,请在射线BF上找一点M,使得以B,M,C为顶点的三角形与△ABP相似,则BM= .
三.解答题
16.如图所示,正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上,EF与BC相交于点G,连接CF.
(1)求证:△DAE≌△DCF;
(2)求证:△ABG∽△CFG.
17.如图所示,在等边中△ABC,D、E分别是AB、AC上的点,DE∥BC,如图(1),然后将△ADE绕A点顺时针旋转120°,使B、A、E三点在同一直线上,得到图(2),M、N分别是BD、CE的中点,连接AM、AN、MN得到图(3),请解答下列问题:
(1)在图(2)中,线段BD与线段CE的大小关系是____________;
(2)在图(3)中,△AMN与△ABC是相似三角形吗?请证明你的结论.
18.如图,点C为线段AB上任意一点(不与A、B两点重合),分别以AC、BC为一腰在AB的同侧作等腰△ACD和等腰△BCE,CA=CD,CB=CE,∠ACD与∠BCE都是锐角且∠ACD=∠BCE,连接AE交CD于点M,连接BD交CE于点N,AE与BD交于点P,连接PC.
(1)求证:△ACE≌△DCB;
(2)请你判断△AMC与△DPM的形状有何关系,并说明理由.
19.如图,在△ABC中,点D、E分别在边BC、AC上,连接AD、DE.且∠B=∠ADE=∠C.
(1)证明:△BDA∽△CED;
(2)若∠B=45°,BC=6,当点D在BC上运动时(点D不与B、C重合).且△ADE是等腰三角形,求此时BD的长.
20.如图,.
(1)求,,的值;
(2)证明与相似.
21.已知抛物线与轴分别交于两点,与轴交于点.
(1)求抛物线的表达式及顶点的坐标;
(2)点是线段上一个动点.
①如图1,设,当为何值时,有.
②如图2,若,求出点的坐标.
22.如图,是的外接圆,,延长到点,使得,连接交于点,过点做的平行线交于点.
(1)求证:;
(2)求证:为的切线;
(3)若,,求弦的长.
参考答案
1.A 2.A 3.C 4.B 5.C 6.A 7.A 8.C 9.C 10.D
11.∠ACP=∠B,或∠APC=∠ACB或=.
12.3
13.①②
14.6
15.2或.
16.【答案】证明 (1)∵四边形ABCD为正方形,△EDF为等腰直角三角形,
∴∠ADC=∠EDF=90°,AD=CD,DE=DF,
∴∠ADE+∠ADF=∠ADF+∠CDF,
∴∠ADE=∠CDF,
在△ADE和△CDF中,
∴△ADE≌△CDF;
(2)延长BA到M,交ED于点M,
∵△ADE≌△CDF,
∴∠EAD=∠FCD,即∠EAM+∠MAD=∠BCD+∠BCF,
∵∠MAD=∠BCD=90°,
∴∠EAM=∠BCF,
∵∠EAM=∠BAG,
∴∠BAG=∠BCF,
∵∠AGB=∠CGF,
∴△ABG∽△CFG.
【解析】(1)由正方形ABCD与等腰直角三角形DEF,得到两对边相等,一对直角相等,利用SAS即可得证;
(2)由第一问的全等三角形的对应角相等,根据等量代换得到∠BAG=∠BCF,再由对顶角相等,利用两对角相等的三角形相似即可得证.
17.【答案】解 (1)BD=CE;
理由:∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
在图(1)中,
∵DE∥BC,
∴△ADE∽△ABC,
∴△ADE是等边三角形,
∵△ADE绕A点顺时针旋转120°,使B、A、E三点在同一直线上,
∴如图(2),AD=AE,∠DAE=60°,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
∴△BAD≌△CAE(SAS),
∴BD=CE;
(2)△AMN与△ABC相似.
证明:∵M、N分别是BD、CE的中点,
∴EN=CE,DM=BD,
∵BD=CE,
∴EN=DM,
∵△BAD≌△CAE,
∴∠AEN=∠ADM,
在△ADM和△AEN中,
∴△ADM≌△AEN(SAS),
∴AM=AN,∠MAD=∠NAE,
∴∠MAN=∠DAE=60°,
∴△AMN也是等边三角形,
∴△AMN∽△ABC.
【解析】(1)由在等边中△ABC,DE∥BC,易证得△ADE也是等边三角形,然后利用SAS,证得△BAD≌△CAE,即可得BD=CE;
(2)由△BAD≌△CAE,可得∠AEN=∠ADM,又由M、N分别是BD、CE的中点,易得EN=DM,然后根据SAS证得△ADM≌△AEN,即可得AM=AN,∠MAN=60°,判定△AMN是等边三角形,即可得在图(3)中,△AMN与△ABC是相似三角形.
18.【答案】(1)证明 ∵∠ACD=∠BCE,
∴∠ACD+∠DCE=∠BCE+∠DCE,
∴∠ACE=∠DCB,
又∵CA=CD,CE=CB,
在△ACE和△DCB中,
∴△ACE≌△DCB(SAS).
(2)解 △AMC∽△DMP.
理由:∵△ACE≌△DCB,
∴∠CAE=∠CDB,
又∵∠AMC=∠DMP,
∴△AMC∽△DMP.
【解析】(1)证明∠ACE=∠DCB,根据“SAS”证明全等;
由(1)得∠CAM=∠PDM,又∠AMC=∠DMP,所以两个三角形相似.
19.【答案】解 (1)连接OA,
∵AB=AC,点A,B,C三点在⊙O上,
∴OA垂直平分BC,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴OA⊥AD,
∴AD是⊙O的切线;
(2)∵AB=AC,
∴∠DEA=∠BCA,
∵AD∥BC,
∴∠DAC=∠BCA,
∴∠DEA=∠DAC,
∵∠D=∠D,
∴△DAC∽△DEA.
【解析】(1)连接OA,根据AB=AC,点A,B,C三点在⊙O上,可得OA垂直平分BC,根据四边形ABCD是平行四边形,得OA⊥AD,即AD是⊙O的切线;
(2)根据AB=AC,∠DEA=∠BCA,再由AD∥BC,得∠DAC=∠BCA,从而得出∠DEA=∠DAC,可证△DAC∽△DEA.
20.【答案】解 乙同学的解答不正确,
与△ABC相似的三角形还有△GFE,应该补上证明如下:
∵DF∥BC,
∴∠GFE=∠ABC,
又∵∠E=∠C,
∴△GFE∽△ABC.
【解析】直接利用相似三角形判定定理得出△GFE∽△ABC即可.
21.解:抛物线过点,
解得:
抛物线解析式为;
顶点的坐标为;
在中,,
,
,
,
,
为直角三角形,且
为的中点,
在中,
在中,
连接 当时,,
设直线的解析式为
解得:
直线的解析式为
直线的解析式为
设直线的解析式为
解得:
直线的解析式为
解得:
22.(1)∵,
∴,
∵,
∴,
∴.
(2)如图,连接,
∵∠DBC=∠BDC,
∴∠ACB=2∠DBC,
∵∠DBC=∠EAC,
∴∠ACB=2∠EAC,
∵AB=BC,
∴∠BAC=∠ACB,
∴∠BAC=2∠EAC,
∴∠EAC=∠EAB,
∴点为的中点,
∴,
∵,
∴,
∴为圆的切线.
(3)在和中,,
∴,
∴,
∴,
∵AB=5,BE=3,
∴
∴,
由(1)得,
∵,
∴,
∵,
∴.
