8.1 成对数据的统计相关性 第八章 成对数据的统计分析 人教A版选择性必修第三册 学案
文档属性
| 名称 | 8.1 成对数据的统计相关性 第八章 成对数据的统计分析 人教A版选择性必修第三册 学案 |

|
|
| 格式 | doc | ||
| 文件大小 | 374.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-21 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第八章 成对数据的统计分析
8.1 成对数据的统计相关性
学习指导 核心素养
1.结合实例,了解样本相关系数的统计含义.2.了解样本相关系数与标准化数据之间的关系.3.结合实例,会通过相关系数比较多组成对数据的相关性. 1.数学抽象:变量的相关关系.2.数据分析:成对数据的实例分析.
1.变量的相关关系
(1)相关关系:两个变量有关系,但又没有确切到可由其中的一个去精确地决定另一个的程度,这种关系称为相关关系.
(2)散点图:把成对样本数据用直角坐标系中的点表示出来,由这些点组成的统计图叫做散点图.
(3)正相关与负相关
①正相关:如果从整体上看,当一个变量的值增加时,另一个变量的相应值也呈现增加的趋势,我们就称这两个变量正相关.
②负相关:如果从整体上看,当一个变量的值增加时,另一个变量的相应值呈现减少的趋势,则称这两个变量负相关.
(4)线性相关与非线性相关(曲线相关)
①线性相关:一般地,如果两个变量的取值呈现正相关或负相关,而且散点落在一条直线附近,我们就称这两个变量线性相关.
②非线性相关(曲线相关):一般地,如果两个变量具有相关性,但不是线性相关,那么我们就称这两个变量非线性相关或曲线相关.
2.样本相关系数
(1)样本相关系数的公式
(2)样本相关系数的意义
样本相关系数r可以反映两个随机变量之间的线性相关程度:r的符号反映了相关关系的正负性;|r|的大小反映了两个变量线性相关的程度,即散点集中于一条直线的程度.
(3)样本相关系数的性质
①|r|≤1.
②当r>0时,称成对样本数据正相关;当r<0时,称成对样本数据负相关.
③当|r|越接近于1时,成对样本数据的线性相关程度越强;当|r|越接近于0时,成对样本数据的线性相关程度越弱.特别地,当|r|=1时,说明成对样本数据都落在一条直线上.
1.变量的相关关系是函数关系吗?
提示:两者是不同概念,比较如下:
(1)相同点:两者均是两个变量之间的关系;
(2)不同点:①函数关系是一种确定的关系,如匀速直线运动中时间t与路程s的关系,相关关系是一种非确定的关系,如一块农田的小麦产量与施肥量之间的关系;
②函数关系是两个随机变量之间的关系,而相关关系是非随机变量与随机变量之间的关系;
③函数关系是一种因果关系,而相关关系不一定是因果关系,也可能是伴随关系.
2.散点图有什么作用?
提示:(1)根据散点图可判断两个变量有无相关关系.
(2)通过散点图不但可以从点的位置判断测量值的大小、变动范围与趋势,还可以通过观察剔除异常数值,提高估计相关程度的准确性.
1.判断正误(正确的打“√”,错误的打“×”)
(1)相关关系是一种非确定性关系,体现的不一定是因果关系,可能是伴随关系.( )
(2)散点图越接近某一条直线,线性相关程度越强,样本相关系数越大.( )
(3)散点图可以直观地分析出两个变量是否具有相关性.( )
(4)若变量x,y满足函数关系,则这两个变量线性相关.( )
答案:(1)√ (2)× (3)√ (4)×
2.(多选)下列关系中,属于相关关系的是( )
A.正方形的边长与面积之间的关系
B.农作物的产量与施肥量之间的关系
C.出租车打车费与行驶的里程
D.降雪量与交通事故的发生率之间的关系
解析:选BD.在A中,正方形的边长与面积之间的关系是函数关系;在B中,农作物的产量与施肥量之间不具有严格的函数关系,但具有相关关系;C为确定的函数关系;在D中,降雪量与交通事故的发生率之间具有相关关系.
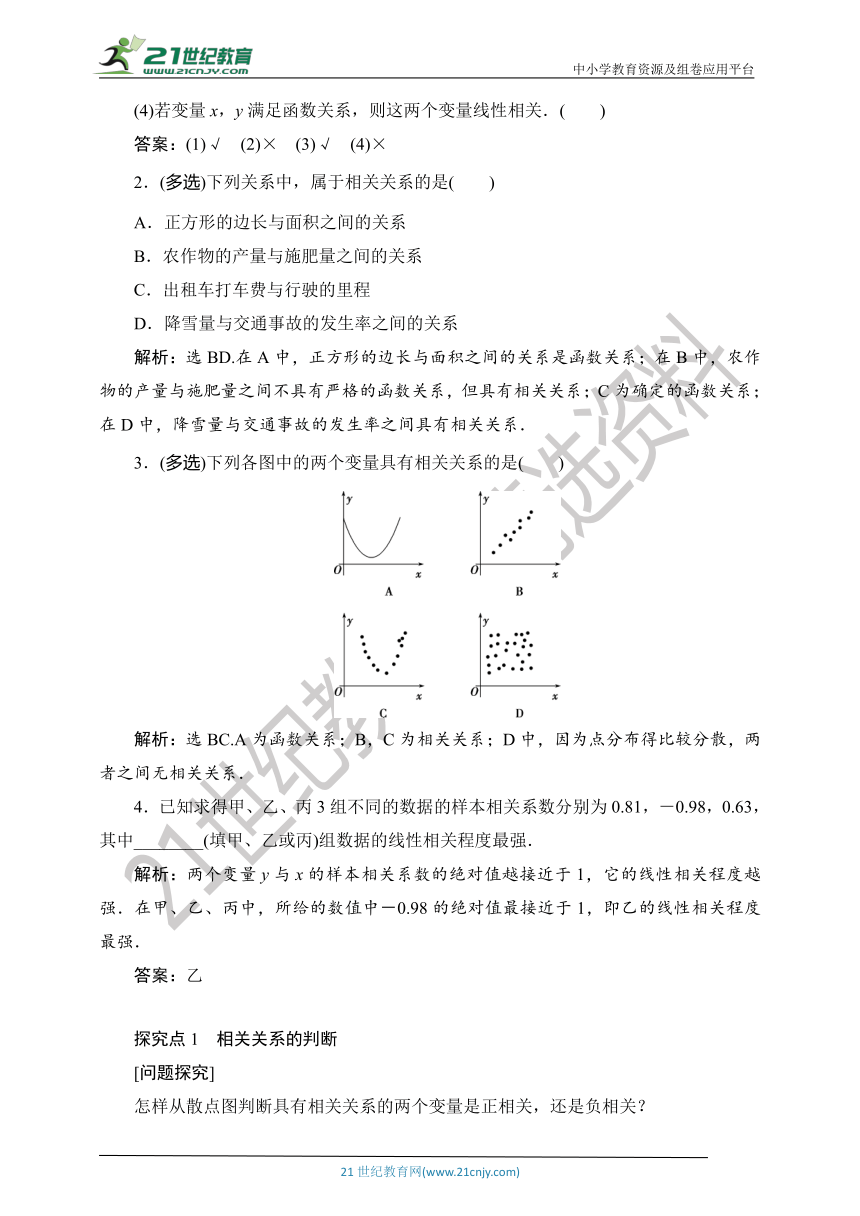
3.(多选)下列各图中的两个变量具有相关关系的是( )
解析:选BC.A为函数关系;B,C为相关关系;D中,因为点分布得比较分散,两者之间无相关关系.
4.已知求得甲、乙、丙3组不同的数据的样本相关系数分别为0.81,-0.98,0.63,其中________(填甲、乙或丙)组数据的线性相关程度最强.
解析:两个变量y与x的样本相关系数的绝对值越接近于1,它的线性相关程度越强.在甲、乙、丙中,所给的数值中-0.98的绝对值最接近于1,即乙的线性相关程度最强.
答案:乙
探究点1 相关关系的判断
[问题探究]
怎样从散点图判断具有相关关系的两个变量是正相关,还是负相关?
探究感悟:从散点图上看,点散布在从左下角到右上角的区域内,两个变量的这种相关关系称为正相关;点散布在从左上角到右下角的区域内,两个变量的相关关系为负相关.
例 以下是某地不同楼盘新房的销售价格y(单位:万元)和面积x(单位:m2)的数据:
面积x(m2) 115 110 80 135 105
销售价格y(万元) 24.8 21.6 19.4 29.2 22
(1)画出数据对应的散点图;
(2)判断新房的销售价格和面积之间是否具有相关关系.如果有相关关系,是正相关还是负相关?
【解】 (1)数据对应的散点图如图所示.
(2)通过以上数据对应的散点图可以判断,新房的销售价格和面积之间具有相关关系,且是正相关.
相关关系的判断方法
(1)两个变量x和y具有相关关系的判断方法
①散点图法:通过散点图,观察它们的分布是否存在一定的规律,直观地判断;
②表格、关系式法:结合表格或关系式进行判断;
③经验法:借助积累的经验进行分析判断.
(2)判断两个变量x和y之间是否具有线性相关关系,常用的简便方法就是绘制散点图,如果发现点的分布从整体上看大致在一条直线附近,那么这两个变量就是线性相关的,注意不要受个别点的位置的影响.
[注意] 在解答题目过程中,易出现如下错误:虽然多数点大致分布在一条直线附近,但少量点离这条直线太远,所以两个变量不相关.导致错误的原因是没有看多数点,而过分关注了不影响大局的个别点.
根据下面给出的2011年至2020年某市二氧化硫排放量(单位:万吨)柱形图.以下结论不正确的是( )
A.逐年比较,2015年减少二氧化硫排放量的效果最显著
B.2014年我国治理二氧化硫排放显现成效
C.2013年以来我国二氧化硫年排放量呈减少趋势
D.2013年以来我国二氧化硫年排放量与年份正相关
解析:选D.由柱形图得,从2013年以来,我国二氧化硫排放量呈下降趋势,故年排放量与年份负相关,故选D.
探究点2 相关性检验
[问题探究]
是否样本相关系数r越大,两个变量间的相关程度越强?
探究感悟:不是.正确结论为|r|越大,两个变量间的相关程度越强.
例 (1)如图所示,给出样本容量均为7的A,B两组样本数据的散点图,已知A组数据的样本相关系数为r1,B组数据的样本相关系数为r2,则( )
A.r1=r2 B.r1C.r1>r2 D.无法判定
(2)为了监控某种零件的一条生产线的生产过程,检验员每隔30 min从该生产线上随机抽取一个零件,并测量其尺寸(单位:cm).下面是检验员在一天内依次抽取的16个零件的尺寸:
抽取次序 1 2 3 4 5 6 7 8
零件尺寸 9.95 10.12 9.96 9.96 10.01 9.92 9.98 10.04
抽取次序 9 10 11 12 13 14 15 16
零件尺寸 10.26 9.91 10.13 10.02 9.22 10.04 10.05 9.95
经计算得=i =9.97,s==≈0.212, eq \r((i-8.5)2)≈18.439,i (xi-)(i-8.5)=-2.78,其中xi为抽取的第i个零件的尺寸,i=1,2,…,16.
求(xi,i)(i=1,2,…,16)的样本相关系数r,并回答是否可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大或变小(若|r|<0.25,则可以认为零件的尺寸不随生产过程的进行而系统地变大或变小).
附:样本(xi,yi)(i=1,2,…,n)的样本相关系数r= .
(1)【解析】 根据A,B两组样本数据的散点图知,A组样本数据几乎在一条直线上,且成正相关,所以样本相关系数r1应最接近1,B组样本数据分散在一条直线附近,也成正相关,所以样本相关系数r2满足r2r2.
【答案】 C
(2)【解】 由样本数据得(xi,i)(i=1,2,…,16)的样本相关系数为
r=≈≈-0.18.
由于|r|<0.25,因此可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大或变小.
相关关系强弱的定量分析与定性分析
(1)定量分析:样本相关系数r的范围为-1≤r≤1,r为正时,成对数据正相关;r为负时,成对数据负相关;|r|越接近1,成对数据的线性相关程度越强;|r|越接近于0,成对数据的线性相关程度越弱;当|r|=1时,所有数据点都在一条直线上.
(2)定性分析:相关关系的强弱体现在散点图中就是样本点越集中在某条直线附近,两变量的线性相关程度越强;样本点在某条直线附近越分散,两变量的线性相关程度越弱.
1.某统计部门对四组成对样本数据进行统计分析后,获得如图所示的散点图,关于样本相关系数的比较,其中正确的是( )
A.r4<r2<0<r1<r3 B.r2<r4<0<r1<r3
C.r2<r4<0<r3<r1 D.r4<r2<0<r3<r1
解析:选C.根据散点图的特征,数据大致呈增长趋势的是正相关,数据大致呈递减趋势的是负相关;数据越集中在一条直线附近,说明相关性越强,由题中数据可知:(1)(3)为正相关,(2)(4)为负相关,故r1>0,r3>0,r2<0,r4<0,又(1)与(2)中散点图更接近于一条直线,故r1>r3>0,r2<r4<0,因此r2<r4<0<r3<r1.故选C.
2.足球是深受全世界人们喜爱的运动,我国大力发展校园足球.为了解本地区足球特色学校的发展状况,社会调查小组得到如下统计数据:
年份x 2016 2017 2018 2019 2020
足球特色
学校y(百个) 0.30 0.60 1.00 1.40 1.70
根据上表数据,计算y与x的样本相关系数r,并说明y与x的线性相关程度.
(已知: 若0.75≤|r|≤1,则认为y与x的线性相关程度很强;若0.3≤|r|<0.75,则认为y与x的线性相关程度一般;|r|≤0.25,则认为y与x的线性相关程度较弱)
解:由题意得=2 018,=1,
所以r==
=≈0.998>0.75,
所以y与x的线性相关程度很强.
当堂自测
1.(多选)下列关于样本相关系数r的说法中正确的是( )
A.样本相关系数r越大两个变量间相关程度越强
B.样本相关系数r的取值范围为[-1,1]
C.样本相关系数r>0时两个变量正相关,r<0时两个变量负相关
D.样本相关系数r=1时,样本点在同一直线上
解析:选BCD.对于样本相关系数r,有以下结论:①当r>0时,表明两个变量正相关;当r<0时,表明两个变量负相关.②r的绝对值越接近于1,表明两个变量的线性相关程度越强;r的绝对值越接近于0,表明两个变量之间几乎不存在线性相关关系.
对于A,当r<0时此结论不成立,所以A不正确;
对于B,由样本相关系数的性质可得-1≤r≤1,所以B正确;
对于C,由样本相关系数的性质可知正确;
对于D,由样本相关系数的性质可知正确.
2.我们常说“吸烟有害健康”,则吸烟与健康之间的关系是( )
A.正相关 B.负相关
C.无相关 D.不确定
解析:选B.烟吸得越多,则健康程度越差.
3.在一次试验中,测得(x,y)的4组值分别为(1,2),(2,0),(4,-4),(-1,6),则y与x的样本相关系数为( )
A.1 B.-2
C.0 D.-1
解析:选D. =1.5,=1,x=22,y=56,x iyi=-20,样本相关系数r==-1.
4.高三年级267位学生参加期末考试,某班37位学生的语文成绩、数学成绩与总成绩在全年级的排名情况如图所示,甲、乙、丙为该班三位学生.从这次考试成绩看:
(1)在甲、乙两人中,其语文成绩名次比其总成绩名次靠前的学生是________;
(2)在语文和数学两个科目中,丙同学的成绩名次更靠前的科目是________.
解析:(1)在甲、乙两人中,其语文成绩名次比其总成绩名次靠前的学生是乙;(2)由高三年级267位学生参加期末考试,某班37位学生的语文成绩、数学成绩与总成绩在全年级的排名情况的散点图可知,两个图中,同一个人的总成绩是不会变的.第二个图看,丙是从右往左数第5个点,即丙的总成绩在班里倒数第5.在左边的图中,找到倒数第5个点,它表示的就是丙,发现这个点的位置比右边图中丙的位置高,所以语文名次更“大”,即数学的成绩更靠前.
答案:(1)乙 (2)数学
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
第八章 成对数据的统计分析
8.1 成对数据的统计相关性
学习指导 核心素养
1.结合实例,了解样本相关系数的统计含义.2.了解样本相关系数与标准化数据之间的关系.3.结合实例,会通过相关系数比较多组成对数据的相关性. 1.数学抽象:变量的相关关系.2.数据分析:成对数据的实例分析.
1.变量的相关关系
(1)相关关系:两个变量有关系,但又没有确切到可由其中的一个去精确地决定另一个的程度,这种关系称为相关关系.
(2)散点图:把成对样本数据用直角坐标系中的点表示出来,由这些点组成的统计图叫做散点图.
(3)正相关与负相关
①正相关:如果从整体上看,当一个变量的值增加时,另一个变量的相应值也呈现增加的趋势,我们就称这两个变量正相关.
②负相关:如果从整体上看,当一个变量的值增加时,另一个变量的相应值呈现减少的趋势,则称这两个变量负相关.
(4)线性相关与非线性相关(曲线相关)
①线性相关:一般地,如果两个变量的取值呈现正相关或负相关,而且散点落在一条直线附近,我们就称这两个变量线性相关.
②非线性相关(曲线相关):一般地,如果两个变量具有相关性,但不是线性相关,那么我们就称这两个变量非线性相关或曲线相关.
2.样本相关系数
(1)样本相关系数的公式
(2)样本相关系数的意义
样本相关系数r可以反映两个随机变量之间的线性相关程度:r的符号反映了相关关系的正负性;|r|的大小反映了两个变量线性相关的程度,即散点集中于一条直线的程度.
(3)样本相关系数的性质
①|r|≤1.
②当r>0时,称成对样本数据正相关;当r<0时,称成对样本数据负相关.
③当|r|越接近于1时,成对样本数据的线性相关程度越强;当|r|越接近于0时,成对样本数据的线性相关程度越弱.特别地,当|r|=1时,说明成对样本数据都落在一条直线上.
1.变量的相关关系是函数关系吗?
提示:两者是不同概念,比较如下:
(1)相同点:两者均是两个变量之间的关系;
(2)不同点:①函数关系是一种确定的关系,如匀速直线运动中时间t与路程s的关系,相关关系是一种非确定的关系,如一块农田的小麦产量与施肥量之间的关系;
②函数关系是两个随机变量之间的关系,而相关关系是非随机变量与随机变量之间的关系;
③函数关系是一种因果关系,而相关关系不一定是因果关系,也可能是伴随关系.
2.散点图有什么作用?
提示:(1)根据散点图可判断两个变量有无相关关系.
(2)通过散点图不但可以从点的位置判断测量值的大小、变动范围与趋势,还可以通过观察剔除异常数值,提高估计相关程度的准确性.
1.判断正误(正确的打“√”,错误的打“×”)
(1)相关关系是一种非确定性关系,体现的不一定是因果关系,可能是伴随关系.( )
(2)散点图越接近某一条直线,线性相关程度越强,样本相关系数越大.( )
(3)散点图可以直观地分析出两个变量是否具有相关性.( )
(4)若变量x,y满足函数关系,则这两个变量线性相关.( )
答案:(1)√ (2)× (3)√ (4)×
2.(多选)下列关系中,属于相关关系的是( )
A.正方形的边长与面积之间的关系
B.农作物的产量与施肥量之间的关系
C.出租车打车费与行驶的里程
D.降雪量与交通事故的发生率之间的关系
解析:选BD.在A中,正方形的边长与面积之间的关系是函数关系;在B中,农作物的产量与施肥量之间不具有严格的函数关系,但具有相关关系;C为确定的函数关系;在D中,降雪量与交通事故的发生率之间具有相关关系.
3.(多选)下列各图中的两个变量具有相关关系的是( )
解析:选BC.A为函数关系;B,C为相关关系;D中,因为点分布得比较分散,两者之间无相关关系.
4.已知求得甲、乙、丙3组不同的数据的样本相关系数分别为0.81,-0.98,0.63,其中________(填甲、乙或丙)组数据的线性相关程度最强.
解析:两个变量y与x的样本相关系数的绝对值越接近于1,它的线性相关程度越强.在甲、乙、丙中,所给的数值中-0.98的绝对值最接近于1,即乙的线性相关程度最强.
答案:乙
探究点1 相关关系的判断
[问题探究]
怎样从散点图判断具有相关关系的两个变量是正相关,还是负相关?
探究感悟:从散点图上看,点散布在从左下角到右上角的区域内,两个变量的这种相关关系称为正相关;点散布在从左上角到右下角的区域内,两个变量的相关关系为负相关.
例 以下是某地不同楼盘新房的销售价格y(单位:万元)和面积x(单位:m2)的数据:
面积x(m2) 115 110 80 135 105
销售价格y(万元) 24.8 21.6 19.4 29.2 22
(1)画出数据对应的散点图;
(2)判断新房的销售价格和面积之间是否具有相关关系.如果有相关关系,是正相关还是负相关?
【解】 (1)数据对应的散点图如图所示.
(2)通过以上数据对应的散点图可以判断,新房的销售价格和面积之间具有相关关系,且是正相关.
相关关系的判断方法
(1)两个变量x和y具有相关关系的判断方法
①散点图法:通过散点图,观察它们的分布是否存在一定的规律,直观地判断;
②表格、关系式法:结合表格或关系式进行判断;
③经验法:借助积累的经验进行分析判断.
(2)判断两个变量x和y之间是否具有线性相关关系,常用的简便方法就是绘制散点图,如果发现点的分布从整体上看大致在一条直线附近,那么这两个变量就是线性相关的,注意不要受个别点的位置的影响.
[注意] 在解答题目过程中,易出现如下错误:虽然多数点大致分布在一条直线附近,但少量点离这条直线太远,所以两个变量不相关.导致错误的原因是没有看多数点,而过分关注了不影响大局的个别点.
根据下面给出的2011年至2020年某市二氧化硫排放量(单位:万吨)柱形图.以下结论不正确的是( )
A.逐年比较,2015年减少二氧化硫排放量的效果最显著
B.2014年我国治理二氧化硫排放显现成效
C.2013年以来我国二氧化硫年排放量呈减少趋势
D.2013年以来我国二氧化硫年排放量与年份正相关
解析:选D.由柱形图得,从2013年以来,我国二氧化硫排放量呈下降趋势,故年排放量与年份负相关,故选D.
探究点2 相关性检验
[问题探究]
是否样本相关系数r越大,两个变量间的相关程度越强?
探究感悟:不是.正确结论为|r|越大,两个变量间的相关程度越强.
例 (1)如图所示,给出样本容量均为7的A,B两组样本数据的散点图,已知A组数据的样本相关系数为r1,B组数据的样本相关系数为r2,则( )
A.r1=r2 B.r1
(2)为了监控某种零件的一条生产线的生产过程,检验员每隔30 min从该生产线上随机抽取一个零件,并测量其尺寸(单位:cm).下面是检验员在一天内依次抽取的16个零件的尺寸:
抽取次序 1 2 3 4 5 6 7 8
零件尺寸 9.95 10.12 9.96 9.96 10.01 9.92 9.98 10.04
抽取次序 9 10 11 12 13 14 15 16
零件尺寸 10.26 9.91 10.13 10.02 9.22 10.04 10.05 9.95
经计算得=i =9.97,s==≈0.212, eq \r((i-8.5)2)≈18.439,i (xi-)(i-8.5)=-2.78,其中xi为抽取的第i个零件的尺寸,i=1,2,…,16.
求(xi,i)(i=1,2,…,16)的样本相关系数r,并回答是否可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大或变小(若|r|<0.25,则可以认为零件的尺寸不随生产过程的进行而系统地变大或变小).
附:样本(xi,yi)(i=1,2,…,n)的样本相关系数r= .
(1)【解析】 根据A,B两组样本数据的散点图知,A组样本数据几乎在一条直线上,且成正相关,所以样本相关系数r1应最接近1,B组样本数据分散在一条直线附近,也成正相关,所以样本相关系数r2满足r2
【答案】 C
(2)【解】 由样本数据得(xi,i)(i=1,2,…,16)的样本相关系数为
r=≈≈-0.18.
由于|r|<0.25,因此可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大或变小.
相关关系强弱的定量分析与定性分析
(1)定量分析:样本相关系数r的范围为-1≤r≤1,r为正时,成对数据正相关;r为负时,成对数据负相关;|r|越接近1,成对数据的线性相关程度越强;|r|越接近于0,成对数据的线性相关程度越弱;当|r|=1时,所有数据点都在一条直线上.
(2)定性分析:相关关系的强弱体现在散点图中就是样本点越集中在某条直线附近,两变量的线性相关程度越强;样本点在某条直线附近越分散,两变量的线性相关程度越弱.
1.某统计部门对四组成对样本数据进行统计分析后,获得如图所示的散点图,关于样本相关系数的比较,其中正确的是( )
A.r4<r2<0<r1<r3 B.r2<r4<0<r1<r3
C.r2<r4<0<r3<r1 D.r4<r2<0<r3<r1
解析:选C.根据散点图的特征,数据大致呈增长趋势的是正相关,数据大致呈递减趋势的是负相关;数据越集中在一条直线附近,说明相关性越强,由题中数据可知:(1)(3)为正相关,(2)(4)为负相关,故r1>0,r3>0,r2<0,r4<0,又(1)与(2)中散点图更接近于一条直线,故r1>r3>0,r2<r4<0,因此r2<r4<0<r3<r1.故选C.
2.足球是深受全世界人们喜爱的运动,我国大力发展校园足球.为了解本地区足球特色学校的发展状况,社会调查小组得到如下统计数据:
年份x 2016 2017 2018 2019 2020
足球特色
学校y(百个) 0.30 0.60 1.00 1.40 1.70
根据上表数据,计算y与x的样本相关系数r,并说明y与x的线性相关程度.
(已知: 若0.75≤|r|≤1,则认为y与x的线性相关程度很强;若0.3≤|r|<0.75,则认为y与x的线性相关程度一般;|r|≤0.25,则认为y与x的线性相关程度较弱)
解:由题意得=2 018,=1,
所以r==
=≈0.998>0.75,
所以y与x的线性相关程度很强.
当堂自测
1.(多选)下列关于样本相关系数r的说法中正确的是( )
A.样本相关系数r越大两个变量间相关程度越强
B.样本相关系数r的取值范围为[-1,1]
C.样本相关系数r>0时两个变量正相关,r<0时两个变量负相关
D.样本相关系数r=1时,样本点在同一直线上
解析:选BCD.对于样本相关系数r,有以下结论:①当r>0时,表明两个变量正相关;当r<0时,表明两个变量负相关.②r的绝对值越接近于1,表明两个变量的线性相关程度越强;r的绝对值越接近于0,表明两个变量之间几乎不存在线性相关关系.
对于A,当r<0时此结论不成立,所以A不正确;
对于B,由样本相关系数的性质可得-1≤r≤1,所以B正确;
对于C,由样本相关系数的性质可知正确;
对于D,由样本相关系数的性质可知正确.
2.我们常说“吸烟有害健康”,则吸烟与健康之间的关系是( )
A.正相关 B.负相关
C.无相关 D.不确定
解析:选B.烟吸得越多,则健康程度越差.
3.在一次试验中,测得(x,y)的4组值分别为(1,2),(2,0),(4,-4),(-1,6),则y与x的样本相关系数为( )
A.1 B.-2
C.0 D.-1
解析:选D. =1.5,=1,x=22,y=56,x iyi=-20,样本相关系数r==-1.
4.高三年级267位学生参加期末考试,某班37位学生的语文成绩、数学成绩与总成绩在全年级的排名情况如图所示,甲、乙、丙为该班三位学生.从这次考试成绩看:
(1)在甲、乙两人中,其语文成绩名次比其总成绩名次靠前的学生是________;
(2)在语文和数学两个科目中,丙同学的成绩名次更靠前的科目是________.
解析:(1)在甲、乙两人中,其语文成绩名次比其总成绩名次靠前的学生是乙;(2)由高三年级267位学生参加期末考试,某班37位学生的语文成绩、数学成绩与总成绩在全年级的排名情况的散点图可知,两个图中,同一个人的总成绩是不会变的.第二个图看,丙是从右往左数第5个点,即丙的总成绩在班里倒数第5.在左边的图中,找到倒数第5个点,它表示的就是丙,发现这个点的位置比右边图中丙的位置高,所以语文名次更“大”,即数学的成绩更靠前.
答案:(1)乙 (2)数学
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
