8.3 列联表与独立性检验 第八章 成对数据的统计分析 人教A版选择性必修第三册 学案
文档属性
| 名称 | 8.3 列联表与独立性检验 第八章 成对数据的统计分析 人教A版选择性必修第三册 学案 | 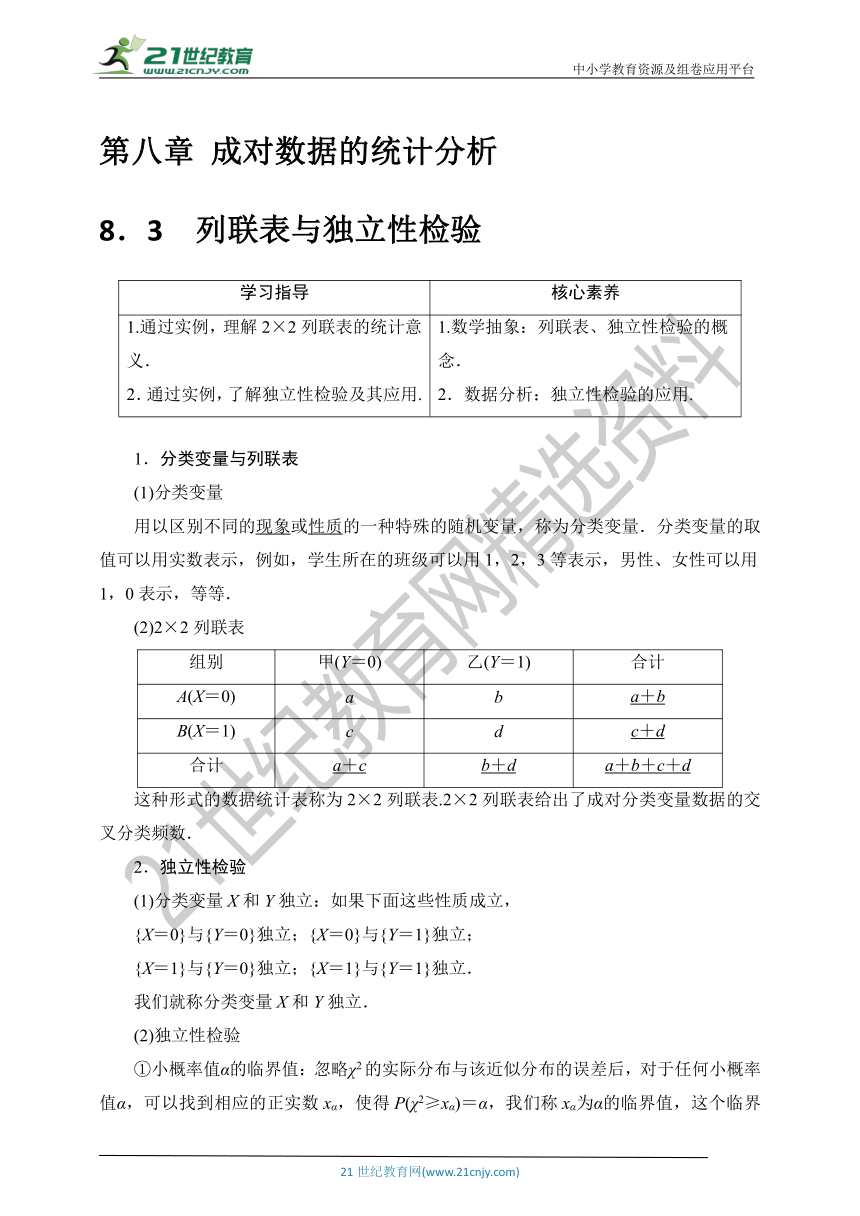 | |
| 格式 | doc | ||
| 文件大小 | 310.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-21 08:31:03 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第八章 成对数据的统计分析
8.3 列联表与独立性检验
学习指导 核心素养
1.通过实例,理解2×2列联表的统计意义.2.通过实例,了解独立性检验及其应用. 1.数学抽象:列联表、独立性检验的概念.2.数据分析:独立性检验的应用.
1.分类变量与列联表
(1)分类变量
用以区别不同的现象或性质的一种特殊的随机变量,称为分类变量.分类变量的取值可以用实数表示,例如,学生所在的班级可以用1,2,3等表示,男性、女性可以用1,0表示,等等.
(2)2×2列联表
组别 甲(Y=0) 乙(Y=1) 合计
A(X=0) a b a+b
B(X=1) c d c+d
合计 a+c b+d a+b+c+d
这种形式的数据统计表称为2×2列联表.2×2列联表给出了成对分类变量数据的交叉分类频数.
2.独立性检验
(1)分类变量X和Y独立:如果下面这些性质成立,
{X=0}与{Y=0}独立;{X=0}与{Y=1}独立;
{X=1}与{Y=0}独立;{X=1}与{Y=1}独立.
我们就称分类变量X和Y独立.
(2)独立性检验
①小概率值α的临界值:忽略χ2的实际分布与该近似分布的误差后,对于任何小概率值α,可以找到相应的正实数xα,使得P(χ2≥xα)=α,我们称xα为α的临界值,这个临界值可作为判断χ2大小的标准.概率值α越小,临界值xα越大.
②χ2的计算公式:
χ2=.
③独立性检验:利用χ2的取值推断分类变量X和Y是否独立的方法称为χ2独立性检验,读作“卡方独立性检验”,简称独立性检验.
④基于小概率值α的检验规则是:
当χ2≥xα时,我们就推断H0不成立,即认为X和Y不独立,该推断犯错误的概率不超过α;当χ2<xα时,我们没有充分证据推断H0不成立,可以认为X和Y独立.(其中xα为α的临界值)
⑤应用独立性检验解决实际问题大致应包括的主要环节:
(ⅰ)提出零假设H0:X和Y相互独立,并给出在问题中的解释.
(ⅱ)根据抽样数据整理出2×2列联表,计算χ2的值,并与临界值xα比较.
(ⅲ)根据检验规则得出推断结论.
(ⅳ)在X和Y不独立的情况下,根据需要,通过比较相应的频率,分析X和Y间的影响规律.
⑥独立性检验中几个常用的小概率值和相应的临界值:
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
1.怎样对两个分类变量的关联性进行定性分析?
提示:(1)频率分析法:通过对样本的每个分类变量的不同类别事件发生的频率大小进行比较来分析分类变量之间是否有关联关系.如可以通过列联表中与值的大小粗略地判断分类变量X和Y之间有无关系.一般其值相差越大,分类变量有关系的可能性越大.
(2)图形分析法:与表格相比,图形更能直观地反映出两个分类变量间是否互相影响,常用等高堆积条形图展示列联表数据的频率特征.
将列联表中的数据用高度相同的两个条形图表示出来,其中两列的数据分别对应不同的颜色,这就是等高堆积条形图.
等高堆积条形图可以展示列联表数据的频率特征,能够直观地反映出两个分类变量间是否相互影响.
2.独立性检验的基本思想和反证法的思想有什么联系?
提示:独立性检验的基本思想与反证法的思想的相似之处:
反证法 独立性检验
要证明结论A 要确认“两个分类变量有关系”
在A不成立的前提下进行推理 假设该结论不成立,即假设“两个分类变量没有关系”成立,在该假设下计算χ2
1.判断正误(正确的打“√”,错误的打“×”)
(1)分类变量中的变量与函数的变量是同一概念.( )
(2)等高堆积条形图可初步分析两分类变量是否有关系,而独立性检验中χ2取值则可通过统计表从数据上说明两分类变量的相关性的大小.( )
(3)事件A与B的独立性检验无关,即两个事件互不影响.( )
(4)χ2的大小是判断事件A与B是否相关的统计量.( )
答案:(1)× (2)√ (3)× (4)√
2.对于独立性检验,下列说法正确的是( )
A.χ2独立性检验的统计假设是各事件之间相互独立
B.χ2可以为负值
C.χ2独立性检验显示“患慢性气管炎和吸烟习惯有关”,这就是指“有吸烟习惯的人必定会患慢性气管炎”
D.2×2列联表中的4个数据可以是任意正数
解析:选A.由独立性检验的检验步骤可知A正确;
因为2×2列联表中的数据均为正整数,故χ2不可能为负值,排除B;
因为χ2独立性检验显示“患慢性气管炎和吸烟习惯有关”,是指有一定的把握说他们相关,或者说有一定的出错率,故排除C;
因为2×2列联表中的4个数据是对于某组特定数据的统计数据,故四个数据间有一定的关系,故排除D.
3.利用独立性检验来考虑两个分类变量X和Y是否有关系时,通过查阅临界值表来确定推断“X和Y有关系”的可信度,如果χ2>5.024,那么就推断“X和Y有关系”,这种推断犯错误的概率不超过( )
α 0.50 0.40 0.25 0.15 0.1
xα 0.455 0.708 1.323 2.072 2.706
α 0.05 0.025 0.01 0.005 0.001
xα 3.841 5.024 6.635 7.879 10.828
A.0.25 B.0.75
C.0.025 D.0.975
解析:选C.因为x0.025=5.024,故在犯错误的概率不超过0.025的前提下,认为“X和Y有关系”.
探究点1 等高堆积条形图的应用
[问题探究]
等高堆积条形图和列联表有什么关系?
探究感悟:(1)列联表与等高堆积条形图都可以用来分析两个分类变量之间是否有关系,但是等高堆积条形图能直观反映出两个分类变量之间是否相互影响,而2×2列联表则需要相关计算才能确定.
(2)等高堆积条形图中,列联表的行对应的是高度,两行的数据不相等,但对应的等高堆积条形图的高度是相同的.
例 网络对现代人的生活影响较大,尤其是对青少年,为了解网络对中学生学习成绩的影响,某地区教育主管部门从辖区初中生中随机抽取了1 000人调查,发现其中经常上网的有200人,这200人中有80人期末考试不及格,而另外800人中有120人不及格.利用图形判断学生经常上网与学习成绩有关吗?
【解】 根据题目所给的数据得到如下2×2列联表:
成绩 上网 合计
经常上网 不经常上网
不及格 80 120 200
及格 120 680 800
合计 200 800 1 000
得到等高堆积条形图如图所示:
比较图中阴影部分,可以发现经常上网期末考试不及格的频率明显高于经常上网期末考试及格的频率,因此可以认为经常上网与学习成绩有关.
判断两个分类变量是否有关系的两种常用方法
(1)利用数形结合思想,借助等高堆积条形图来判断两个分类变量是否相关是判断变量是否相关的常见方法.
(2)一般地,在等高堆积条形图中,与相差越大,两个分类变量有关系的可能性就越大.
某生产线上,质量监督员甲在生产现场时,990件产品中有合格品982件,次品8件;不在生产现场时,510件产品中有合格品493件,次品17件.试利用列联表和等高堆积条形图判断监督员甲在不在生产现场对产品质量好坏有无影响.
解:根据题目所给数据得如下2×2列联表:
合格品数 次品数 合计
甲在生产现场 982 8 990
甲不在生产现场 493 17 510
合计 1 475 25 1 500
所以ad-bc=982×17-8×493=12 750,|ad-bc|比较大,说明甲在不在生产现场与产品质量好坏有关系.相应的等高堆积条形图如图所示:
图中两个阴影部分的高分别表示甲在生产现场和甲不在生产现场时样本中次品数的频率.从图中可以看出,甲不在生产现场时样本中次品数的频率明显高于甲在生产现场时样本中次品数的频率.因此可以认为质量监督员甲在不在生产现场与产品质量好坏有关系.
探究点2 独立性检验
[问题探究]
独立性检验得出的结论“两个变量x,y有关联”,是否为确定性结论?
探究感悟:独立性检验得出的结论是带有概率性质的,只能说结论成立的概率有多大,而不能完全肯定一个结论.
例 (2021·吉林四平高三检验)为了研究每周累计户外暴露时间是否足够(单位:小时)与近视发病率的关系,对某中学一年级100名学生进行不记名问卷调查,得到如下数据:
近视 不近视
足够的户外暴露时间 20 35
不足够的户外暴露时间 30 15
(1)用样本估计总体思想估计该中学一年级学生的近视率;
(2)能否在犯错误的概率不超过0.01的前提下认为不足够的户外暴露时间与近视有关系?
【解】 (1)零假设为H0:户外暴露时间与近视率相互独立.由题可知该中学一年级学生近视的人数为50,总数为100,利用样本估计总体思想可知该中学一年级学生的近视率为×100%=50%.
(2)由题可知n=100,a=20,b=35,c=30,d=15,故χ2==
≈9.091>6.635=x0.01.
在犯错误的概率不超过0.01的前提下可以推断H0不成立,即认为不足够的户外暴露时间与近视有关系.
本例中能否在犯错误的概率不超过0.001的前提下认为不足够的户外暴露时间与近视有关系?
解:由例题解法可知χ2=9.091<10.828=x0.001,所以没有充分证据推断H0不成立,故在犯错误的概率不超过0.001的前提下不能认为不足够的户外暴露时间与近视有关系.
解决独立性检验问题的基本步骤
(2021·河南省南阳市期中)为了检验两种不同的课堂教学模式对学生的成绩是否有影响,现从高二年级的甲(实行“问题—探究式”模式)、乙(实行“自学—指导式”模式)两个班中每班任意抽取20名学生进行测试,他们的成绩(总分150分)如下.
甲班:88 92 95 98 103 108 110 112 118 118
120 121 126 132 134 135 140 142 146 148
乙班:96 97 104 107 108 108 114 117 119 121 124 124 125 127 132 135 135 137 138
147
记成绩在120分以上(包括120分)为优秀,其他的成绩为一般,试根据小概率值α=0.1的独立性检验,分析这两种课堂教学模式对学生的成绩是否有影响.
解:零假设为H0:课堂教学模式与学生的成绩相互独立.根据题中所给数据得到如下2×2列联表:
班级 成绩 合计
优秀 一般
甲班 10 10 20
乙班 11 9 20
合计 21 19 40
所以χ2==≈0.100 3<2.706=x0.1,依据小概率值α=0.1的独立性检验,没有充分证据推断H0不成立,因此可以认为H0成立,即认为这两种课堂教学模式对学生的成绩没有影响.
当堂自测
1.某飞机在一次飞行航程中遭遇恶劣气候,55名男乘客中有24名晕机,34名女乘客中有8名晕机,在检验这些乘客晕机是否与性别有关时,采用的数据分析方法应是( )
A.频率分布直方图 B.回归分析
C.独立性检验 D.用样本估计总体
解析:选C.根据题意,结合题目中的数据,列出2×2列联表,求出χ2,对照数表可得出概率结论,这种分析数据的方法是独立性检验.
2.如表是一个2×2列联表,则表中a,b的值分别为( )
y1 y2 合计
x1 a 21 73
x2 22 25 47
合计 b 46 120
A.94,72 B.52,50
C.52,74 D.74,52
解析:选C.a=73-21=52,b=a+22=52+22=74.
3.以下关于独立性检验的说法中,错误的是( )
A.独立性检验的依据是小概率原理
B.独立性检验的结论一定正确
C.样本不同,独立检验的结论可能有差异
D.独立性检验不是判定两个分类变量是否相关的唯一方法
解析:选B.独立性检验会犯随机性错误,犯错误的概率不会超过小概率值.
4.为研究某新药的疗效,给100名患者服用此药,跟踪调查后得下表中的数据:
无效 有效 合计
男性患者 15 35 50
女性患者 6 44 50
合计 21 79 100
零假设为H0:服用此药的效果与患者的性别无关,则χ2≈________,从而得出结论:服用此药的效果与患者的性别有关,这种判断出错的可能性为________.
解析:由公式计算得χ2≈4.882.
因为χ2>3.841=x0.05,所以我们有95%的把握认为服用此药的效果与患者的性别有关,从而出错的可能性为5%.
答案:4.882 5%
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
第八章 成对数据的统计分析
8.3 列联表与独立性检验
学习指导 核心素养
1.通过实例,理解2×2列联表的统计意义.2.通过实例,了解独立性检验及其应用. 1.数学抽象:列联表、独立性检验的概念.2.数据分析:独立性检验的应用.
1.分类变量与列联表
(1)分类变量
用以区别不同的现象或性质的一种特殊的随机变量,称为分类变量.分类变量的取值可以用实数表示,例如,学生所在的班级可以用1,2,3等表示,男性、女性可以用1,0表示,等等.
(2)2×2列联表
组别 甲(Y=0) 乙(Y=1) 合计
A(X=0) a b a+b
B(X=1) c d c+d
合计 a+c b+d a+b+c+d
这种形式的数据统计表称为2×2列联表.2×2列联表给出了成对分类变量数据的交叉分类频数.
2.独立性检验
(1)分类变量X和Y独立:如果下面这些性质成立,
{X=0}与{Y=0}独立;{X=0}与{Y=1}独立;
{X=1}与{Y=0}独立;{X=1}与{Y=1}独立.
我们就称分类变量X和Y独立.
(2)独立性检验
①小概率值α的临界值:忽略χ2的实际分布与该近似分布的误差后,对于任何小概率值α,可以找到相应的正实数xα,使得P(χ2≥xα)=α,我们称xα为α的临界值,这个临界值可作为判断χ2大小的标准.概率值α越小,临界值xα越大.
②χ2的计算公式:
χ2=.
③独立性检验:利用χ2的取值推断分类变量X和Y是否独立的方法称为χ2独立性检验,读作“卡方独立性检验”,简称独立性检验.
④基于小概率值α的检验规则是:
当χ2≥xα时,我们就推断H0不成立,即认为X和Y不独立,该推断犯错误的概率不超过α;当χ2<xα时,我们没有充分证据推断H0不成立,可以认为X和Y独立.(其中xα为α的临界值)
⑤应用独立性检验解决实际问题大致应包括的主要环节:
(ⅰ)提出零假设H0:X和Y相互独立,并给出在问题中的解释.
(ⅱ)根据抽样数据整理出2×2列联表,计算χ2的值,并与临界值xα比较.
(ⅲ)根据检验规则得出推断结论.
(ⅳ)在X和Y不独立的情况下,根据需要,通过比较相应的频率,分析X和Y间的影响规律.
⑥独立性检验中几个常用的小概率值和相应的临界值:
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
1.怎样对两个分类变量的关联性进行定性分析?
提示:(1)频率分析法:通过对样本的每个分类变量的不同类别事件发生的频率大小进行比较来分析分类变量之间是否有关联关系.如可以通过列联表中与值的大小粗略地判断分类变量X和Y之间有无关系.一般其值相差越大,分类变量有关系的可能性越大.
(2)图形分析法:与表格相比,图形更能直观地反映出两个分类变量间是否互相影响,常用等高堆积条形图展示列联表数据的频率特征.
将列联表中的数据用高度相同的两个条形图表示出来,其中两列的数据分别对应不同的颜色,这就是等高堆积条形图.
等高堆积条形图可以展示列联表数据的频率特征,能够直观地反映出两个分类变量间是否相互影响.
2.独立性检验的基本思想和反证法的思想有什么联系?
提示:独立性检验的基本思想与反证法的思想的相似之处:
反证法 独立性检验
要证明结论A 要确认“两个分类变量有关系”
在A不成立的前提下进行推理 假设该结论不成立,即假设“两个分类变量没有关系”成立,在该假设下计算χ2
1.判断正误(正确的打“√”,错误的打“×”)
(1)分类变量中的变量与函数的变量是同一概念.( )
(2)等高堆积条形图可初步分析两分类变量是否有关系,而独立性检验中χ2取值则可通过统计表从数据上说明两分类变量的相关性的大小.( )
(3)事件A与B的独立性检验无关,即两个事件互不影响.( )
(4)χ2的大小是判断事件A与B是否相关的统计量.( )
答案:(1)× (2)√ (3)× (4)√
2.对于独立性检验,下列说法正确的是( )
A.χ2独立性检验的统计假设是各事件之间相互独立
B.χ2可以为负值
C.χ2独立性检验显示“患慢性气管炎和吸烟习惯有关”,这就是指“有吸烟习惯的人必定会患慢性气管炎”
D.2×2列联表中的4个数据可以是任意正数
解析:选A.由独立性检验的检验步骤可知A正确;
因为2×2列联表中的数据均为正整数,故χ2不可能为负值,排除B;
因为χ2独立性检验显示“患慢性气管炎和吸烟习惯有关”,是指有一定的把握说他们相关,或者说有一定的出错率,故排除C;
因为2×2列联表中的4个数据是对于某组特定数据的统计数据,故四个数据间有一定的关系,故排除D.
3.利用独立性检验来考虑两个分类变量X和Y是否有关系时,通过查阅临界值表来确定推断“X和Y有关系”的可信度,如果χ2>5.024,那么就推断“X和Y有关系”,这种推断犯错误的概率不超过( )
α 0.50 0.40 0.25 0.15 0.1
xα 0.455 0.708 1.323 2.072 2.706
α 0.05 0.025 0.01 0.005 0.001
xα 3.841 5.024 6.635 7.879 10.828
A.0.25 B.0.75
C.0.025 D.0.975
解析:选C.因为x0.025=5.024,故在犯错误的概率不超过0.025的前提下,认为“X和Y有关系”.
探究点1 等高堆积条形图的应用
[问题探究]
等高堆积条形图和列联表有什么关系?
探究感悟:(1)列联表与等高堆积条形图都可以用来分析两个分类变量之间是否有关系,但是等高堆积条形图能直观反映出两个分类变量之间是否相互影响,而2×2列联表则需要相关计算才能确定.
(2)等高堆积条形图中,列联表的行对应的是高度,两行的数据不相等,但对应的等高堆积条形图的高度是相同的.
例 网络对现代人的生活影响较大,尤其是对青少年,为了解网络对中学生学习成绩的影响,某地区教育主管部门从辖区初中生中随机抽取了1 000人调查,发现其中经常上网的有200人,这200人中有80人期末考试不及格,而另外800人中有120人不及格.利用图形判断学生经常上网与学习成绩有关吗?
【解】 根据题目所给的数据得到如下2×2列联表:
成绩 上网 合计
经常上网 不经常上网
不及格 80 120 200
及格 120 680 800
合计 200 800 1 000
得到等高堆积条形图如图所示:
比较图中阴影部分,可以发现经常上网期末考试不及格的频率明显高于经常上网期末考试及格的频率,因此可以认为经常上网与学习成绩有关.
判断两个分类变量是否有关系的两种常用方法
(1)利用数形结合思想,借助等高堆积条形图来判断两个分类变量是否相关是判断变量是否相关的常见方法.
(2)一般地,在等高堆积条形图中,与相差越大,两个分类变量有关系的可能性就越大.
某生产线上,质量监督员甲在生产现场时,990件产品中有合格品982件,次品8件;不在生产现场时,510件产品中有合格品493件,次品17件.试利用列联表和等高堆积条形图判断监督员甲在不在生产现场对产品质量好坏有无影响.
解:根据题目所给数据得如下2×2列联表:
合格品数 次品数 合计
甲在生产现场 982 8 990
甲不在生产现场 493 17 510
合计 1 475 25 1 500
所以ad-bc=982×17-8×493=12 750,|ad-bc|比较大,说明甲在不在生产现场与产品质量好坏有关系.相应的等高堆积条形图如图所示:
图中两个阴影部分的高分别表示甲在生产现场和甲不在生产现场时样本中次品数的频率.从图中可以看出,甲不在生产现场时样本中次品数的频率明显高于甲在生产现场时样本中次品数的频率.因此可以认为质量监督员甲在不在生产现场与产品质量好坏有关系.
探究点2 独立性检验
[问题探究]
独立性检验得出的结论“两个变量x,y有关联”,是否为确定性结论?
探究感悟:独立性检验得出的结论是带有概率性质的,只能说结论成立的概率有多大,而不能完全肯定一个结论.
例 (2021·吉林四平高三检验)为了研究每周累计户外暴露时间是否足够(单位:小时)与近视发病率的关系,对某中学一年级100名学生进行不记名问卷调查,得到如下数据:
近视 不近视
足够的户外暴露时间 20 35
不足够的户外暴露时间 30 15
(1)用样本估计总体思想估计该中学一年级学生的近视率;
(2)能否在犯错误的概率不超过0.01的前提下认为不足够的户外暴露时间与近视有关系?
【解】 (1)零假设为H0:户外暴露时间与近视率相互独立.由题可知该中学一年级学生近视的人数为50,总数为100,利用样本估计总体思想可知该中学一年级学生的近视率为×100%=50%.
(2)由题可知n=100,a=20,b=35,c=30,d=15,故χ2==
≈9.091>6.635=x0.01.
在犯错误的概率不超过0.01的前提下可以推断H0不成立,即认为不足够的户外暴露时间与近视有关系.
本例中能否在犯错误的概率不超过0.001的前提下认为不足够的户外暴露时间与近视有关系?
解:由例题解法可知χ2=9.091<10.828=x0.001,所以没有充分证据推断H0不成立,故在犯错误的概率不超过0.001的前提下不能认为不足够的户外暴露时间与近视有关系.
解决独立性检验问题的基本步骤
(2021·河南省南阳市期中)为了检验两种不同的课堂教学模式对学生的成绩是否有影响,现从高二年级的甲(实行“问题—探究式”模式)、乙(实行“自学—指导式”模式)两个班中每班任意抽取20名学生进行测试,他们的成绩(总分150分)如下.
甲班:88 92 95 98 103 108 110 112 118 118
120 121 126 132 134 135 140 142 146 148
乙班:96 97 104 107 108 108 114 117 119 121 124 124 125 127 132 135 135 137 138
147
记成绩在120分以上(包括120分)为优秀,其他的成绩为一般,试根据小概率值α=0.1的独立性检验,分析这两种课堂教学模式对学生的成绩是否有影响.
解:零假设为H0:课堂教学模式与学生的成绩相互独立.根据题中所给数据得到如下2×2列联表:
班级 成绩 合计
优秀 一般
甲班 10 10 20
乙班 11 9 20
合计 21 19 40
所以χ2==≈0.100 3<2.706=x0.1,依据小概率值α=0.1的独立性检验,没有充分证据推断H0不成立,因此可以认为H0成立,即认为这两种课堂教学模式对学生的成绩没有影响.
当堂自测
1.某飞机在一次飞行航程中遭遇恶劣气候,55名男乘客中有24名晕机,34名女乘客中有8名晕机,在检验这些乘客晕机是否与性别有关时,采用的数据分析方法应是( )
A.频率分布直方图 B.回归分析
C.独立性检验 D.用样本估计总体
解析:选C.根据题意,结合题目中的数据,列出2×2列联表,求出χ2,对照数表可得出概率结论,这种分析数据的方法是独立性检验.
2.如表是一个2×2列联表,则表中a,b的值分别为( )
y1 y2 合计
x1 a 21 73
x2 22 25 47
合计 b 46 120
A.94,72 B.52,50
C.52,74 D.74,52
解析:选C.a=73-21=52,b=a+22=52+22=74.
3.以下关于独立性检验的说法中,错误的是( )
A.独立性检验的依据是小概率原理
B.独立性检验的结论一定正确
C.样本不同,独立检验的结论可能有差异
D.独立性检验不是判定两个分类变量是否相关的唯一方法
解析:选B.独立性检验会犯随机性错误,犯错误的概率不会超过小概率值.
4.为研究某新药的疗效,给100名患者服用此药,跟踪调查后得下表中的数据:
无效 有效 合计
男性患者 15 35 50
女性患者 6 44 50
合计 21 79 100
零假设为H0:服用此药的效果与患者的性别无关,则χ2≈________,从而得出结论:服用此药的效果与患者的性别有关,这种判断出错的可能性为________.
解析:由公式计算得χ2≈4.882.
因为χ2>3.841=x0.05,所以我们有95%的把握认为服用此药的效果与患者的性别有关,从而出错的可能性为5%.
答案:4.882 5%
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
