北师大版八年级数学下册 6.1 平行四边形的性质(1) 课件(共20张PPT)
文档属性
| 名称 | 北师大版八年级数学下册 6.1 平行四边形的性质(1) 课件(共20张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 522.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-20 07:47:22 | ||
图片预览








文档简介
(共20张PPT)
在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。
——毕达哥拉斯
第六章 平行四边形
1 平行四边形的性质(一)
教学目标:
1.经历探索平行四边形有关概念和性质的过程,在活动
中发展学生的探究意识和合作交流的习惯;
2.索并掌握平行四边形的性质,并能简单应用;
3.在探索活动过程中发展学生的探究意识。
教学重点:平行四边形性质的探索。
教学难点:平行四边形性质的理解。
交流预习
教师提问
1、平行线有哪些特征?怎样识别平行线?
2、全等三角形有哪些性质?
3、四边形的内角和是多少度?
4、如图四边形ABCD中AB//CD、AD//BC ∠B=600请你求出其他各角度数
A
B
C
D
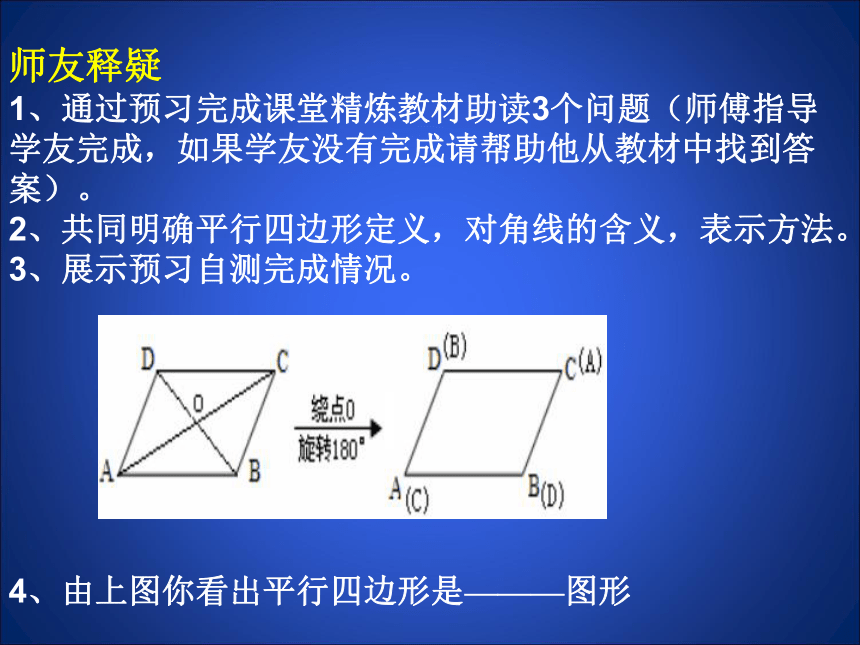
师友释疑
1、通过预习完成课堂精炼教材助读3个问题(师傅指导
学友完成,如果学友没有完成请帮助他从教材中找到答
案)。
2、共同明确平行四边形定义,对角线的含义,表示方法。
3、展示预习自测完成情况。
4、由上图你看出平行四边形是———图形
结论1:平行四边形是中心对称图形,
两条对角线的交点是他的对称中心
结论:
平行四边形的对边平行且相等。
平行四边形的对角相等。
∵ 四边形ABCD是平行四边形
∴ AB=DC , AD=BC.
∠A=∠C , ∠B=∠D.
∴ AB∥DC, AD∥BC
师友探究:平行四边形的对边、对角分别有 什么关系?
A
B
C
D
互助探究
可以通过推理来证明这个结论:
例:如图6-2(1),四边形ABCD是平行四边形.
求证:AB=CD,BC=DA.
证明:如图6-2(2),连接AC.
∵ 四边形ABCD是平行四边形
∴ AD // BC,AB // CD
∴ ∠1=∠2,∠3=∠4
∴ △ABC和△CDA中
∠2=∠1
AC=CA
∠3=∠4
∴ △ABC≌△CDA(ASA)
∴ AB=DC, AD=CB
1
2
3
4
你能证明平行四边形的对角相等吗?
如图6-2(1),四边形ABCD是平行四边形.
求证: ∠A=∠C,∠B=∠D.
证明:如图连接AC.
∵ 四边形ABCD是平行四边形
∴ AD // BC, AB // CD
∴ ∠A+∠B=180 °
∠A+∠D=180 °
∴ ∠B=∠D
同理可得:∠A=∠C
1
2
3
4
平行四边形的对边平行且相等。
平行四边形的对角相等。
∵ 四边形ABCD是平行四边形
∴ AB=DC , AD=BC.
∠A=∠C , ∠B=∠D.
∴ AB∥DC, AD∥BC
教师讲解:
A
B
C
D
推理格式
命题的证明要有完整的
三步:1、写已知求证
2、画图。3、证明。
师友训练
1. ABCD中, ∠B=600,则∠A=——, ∠C=——, ∠D=——.
2. ABCD中∠A比∠B大200,则∠C=——.
ABCD中,AB=3cm,BC=5cm,
则AD=——,CD=——.
4.如果 ABCD的周长为40cm, ABC的周长为25cm,则对角线AC的长是( ).
A 5cm B 15cm C 6cm D 16cm
1200
1200
600
1000
5cm
3cm
A
分层提高
5、已知:如图6-3,在平行四边形ABCD中,
E,F 是对角线AC上的两点,且AE=CF.
求证:BE = DF.
证明:∵四边形ABCD是平行四边形
∴AB = CD
AB // CD
∴∠BAE=∠DCF
又∵AE=CF
∴△BAE≌△DCF
∴BE=DF
要利用新学的知识及几何语言解决问题
教师提升
师友归纳
学到了那些知识。
2.这节课与同伴合作交流中,你和同伴解决了哪些问题?
3.本节课在知识和方法对你有什么启发
归纳总结
A
B
C
D
对角线 :平行四边形不相邻的两个
顶点连成的线段
平行四边形的概念
平行四边形:两组对边分别平行的四边形是平行四边形。
平行四边形记法: ABCD
读作:平行四边形ABCD
教师总结
平行四边形的对称性——中心对称
平行四边形的性质:
平行四边形的对边相等
平行四边形的对角相等
师友检测:师友共同完成习题6.1
巩固反馈
教师评价:
把一件平凡的事情做好就是不平凡
把一件简单的事情做好就是不简单
在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。
——毕达哥拉斯
第六章 平行四边形
1 平行四边形的性质(一)
教学目标:
1.经历探索平行四边形有关概念和性质的过程,在活动
中发展学生的探究意识和合作交流的习惯;
2.索并掌握平行四边形的性质,并能简单应用;
3.在探索活动过程中发展学生的探究意识。
教学重点:平行四边形性质的探索。
教学难点:平行四边形性质的理解。
交流预习
教师提问
1、平行线有哪些特征?怎样识别平行线?
2、全等三角形有哪些性质?
3、四边形的内角和是多少度?
4、如图四边形ABCD中AB//CD、AD//BC ∠B=600请你求出其他各角度数
A
B
C
D
师友释疑
1、通过预习完成课堂精炼教材助读3个问题(师傅指导
学友完成,如果学友没有完成请帮助他从教材中找到答
案)。
2、共同明确平行四边形定义,对角线的含义,表示方法。
3、展示预习自测完成情况。
4、由上图你看出平行四边形是———图形
结论1:平行四边形是中心对称图形,
两条对角线的交点是他的对称中心
结论:
平行四边形的对边平行且相等。
平行四边形的对角相等。
∵ 四边形ABCD是平行四边形
∴ AB=DC , AD=BC.
∠A=∠C , ∠B=∠D.
∴ AB∥DC, AD∥BC
师友探究:平行四边形的对边、对角分别有 什么关系?
A
B
C
D
互助探究
可以通过推理来证明这个结论:
例:如图6-2(1),四边形ABCD是平行四边形.
求证:AB=CD,BC=DA.
证明:如图6-2(2),连接AC.
∵ 四边形ABCD是平行四边形
∴ AD // BC,AB // CD
∴ ∠1=∠2,∠3=∠4
∴ △ABC和△CDA中
∠2=∠1
AC=CA
∠3=∠4
∴ △ABC≌△CDA(ASA)
∴ AB=DC, AD=CB
1
2
3
4
你能证明平行四边形的对角相等吗?
如图6-2(1),四边形ABCD是平行四边形.
求证: ∠A=∠C,∠B=∠D.
证明:如图连接AC.
∵ 四边形ABCD是平行四边形
∴ AD // BC, AB // CD
∴ ∠A+∠B=180 °
∠A+∠D=180 °
∴ ∠B=∠D
同理可得:∠A=∠C
1
2
3
4
平行四边形的对边平行且相等。
平行四边形的对角相等。
∵ 四边形ABCD是平行四边形
∴ AB=DC , AD=BC.
∠A=∠C , ∠B=∠D.
∴ AB∥DC, AD∥BC
教师讲解:
A
B
C
D
推理格式
命题的证明要有完整的
三步:1、写已知求证
2、画图。3、证明。
师友训练
1. ABCD中, ∠B=600,则∠A=——, ∠C=——, ∠D=——.
2. ABCD中∠A比∠B大200,则∠C=——.
ABCD中,AB=3cm,BC=5cm,
则AD=——,CD=——.
4.如果 ABCD的周长为40cm, ABC的周长为25cm,则对角线AC的长是( ).
A 5cm B 15cm C 6cm D 16cm
1200
1200
600
1000
5cm
3cm
A
分层提高
5、已知:如图6-3,在平行四边形ABCD中,
E,F 是对角线AC上的两点,且AE=CF.
求证:BE = DF.
证明:∵四边形ABCD是平行四边形
∴AB = CD
AB // CD
∴∠BAE=∠DCF
又∵AE=CF
∴△BAE≌△DCF
∴BE=DF
要利用新学的知识及几何语言解决问题
教师提升
师友归纳
学到了那些知识。
2.这节课与同伴合作交流中,你和同伴解决了哪些问题?
3.本节课在知识和方法对你有什么启发
归纳总结
A
B
C
D
对角线 :平行四边形不相邻的两个
顶点连成的线段
平行四边形的概念
平行四边形:两组对边分别平行的四边形是平行四边形。
平行四边形记法: ABCD
读作:平行四边形ABCD
教师总结
平行四边形的对称性——中心对称
平行四边形的性质:
平行四边形的对边相等
平行四边形的对角相等
师友检测:师友共同完成习题6.1
巩固反馈
教师评价:
把一件平凡的事情做好就是不平凡
把一件简单的事情做好就是不简单
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
