人教版九年级上册数学 24.2.2 直线和圆的位置关系 教案
文档属性
| 名称 | 人教版九年级上册数学 24.2.2 直线和圆的位置关系 教案 |  | |
| 格式 | doc | ||
| 文件大小 | 115.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-20 13:54:38 | ||
图片预览

文档简介
直线和圆的位置关系
学习目标:
1.了解直线和圆的位置关系的有关概念.
2.理解设⊙O的半径为r,直线L到圆心O的距离为d,则有:
直线L和⊙O相交 dr.
重点、难点
1、 重点:探索直线和圆的三种位置关系
2、 难点:探索直线和圆的三种位置关系及应用直线和圆的位置关系解决问题。
导学过程:阅读教材P93 —94 , 完成课前预习
【课前预习】
1:知识准备
点与圆的位置关系 数量关系
2:探究1:
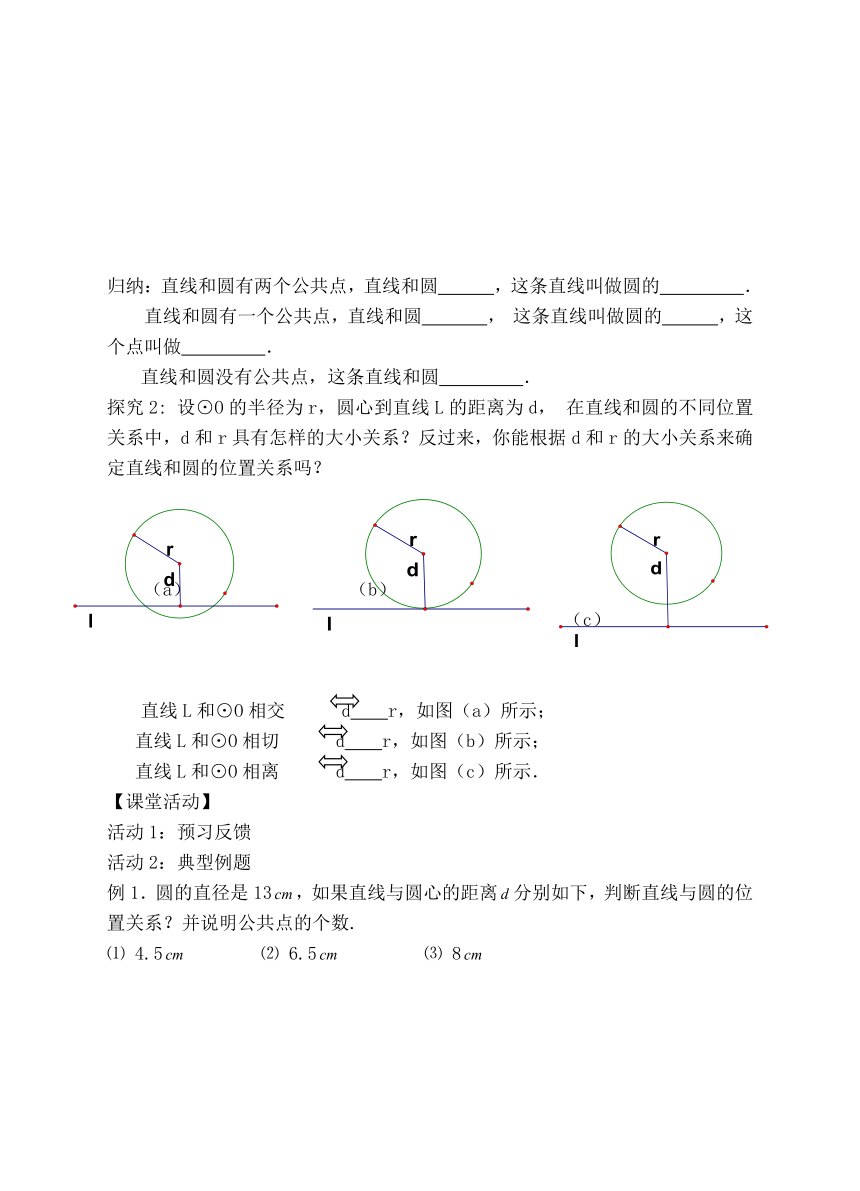
(1)你看过日出吗?你知道太阳升起过程中,太阳和地平线会有几种不同位置关系吗?
(2)如图,在纸上画一条直线 L,把钥匙环看作一个圆,在纸上移动钥匙环,你能发现在钥匙环移动的过程中,它与直线L的公共点的个数吗?
发现:直线与圆有如下三种位置关系:
归纳:直线和圆有两个公共点,直线和圆 ,这条直线叫做圆的 .
直线和圆有一个公共点,直线和圆 ,这条直线叫做圆的 ,这个点叫做 .
直线和圆没有公共点,这条直线和圆 .
探究2: 设⊙O的半径为r,圆心到直线L的距离为d,在直线和圆的不同位置关系中,d和r具有怎样的大小关系?反过来,你能根据d和r的大小关系来确定直线和圆的位置关系吗?
(a) (b)
(c)
直线L和⊙O相交 d r,如图(a)所示;
直线L和⊙O相切 d r,如图(b)所示;
直线L和⊙O相离 d r,如图(c)所示.
【课堂活动】
活动1:预习反馈
活动2:典型例题
例1.圆的直径是13,如果直线与圆心的距离分别如下,判断直线与圆的位置关系?并说明公共点的个数.
⑴ 4.5 ⑵ 6.5 ⑶ 8
例2.在 Rt△ABC 中,∠C = 90°,AC = 3 cm , BC = 4 cm ,以 C 为圆心,下列r 为半径的圆与AB有怎样的位置关系?
⑴r=2cm ⑵r=2.4cm ⑶r=3cm
活动3:随堂训练
1.⊙O的半径是5,点O到直线l的距离为4,则直线l与⊙O的位置关系为( )
A.相离 B.相切 C.相交 D.相交或相切
2.如果⊙O的直径为6厘米,圆心O到直线AB的距离为5厘米,则直线与AB的位置关系为( )
A.相离 B.相切 C.相交 D.不确定
3、已知⊙O的直径为10.
(1)、若直线与⊙O相交,则圆心O到直线的距离d ________;
(2)、若直线与⊙O相切,则圆心O到直线的距离d ________;
(3)、若直线与⊙O相离,则圆心O到直线的距离d ________.
4、已知⊙A的直径为6,点A的坐标为(-3,-4),则⊙A与X轴的位置关系是_____,⊙A与Y轴的位置关系是______。
5、已知△ABC 中,AB=AC=5,BC=6,以点A为圆心,以4为半径作⊙A ,⊙A 与直线BC的位置关系怎样。
活动4:课堂小结
1、直线和圆的位置关系表:
直线和圆的位置关系 相交 相切 相离
公共点的个数
公共点名称
直线名称
圆心到直线的距离d与r的关系
2、确定直线与圆的位置关系的方法有____种
(1)根据定义,由___________ _______的个数来判断;
(2)根据性质,由_________________________ 的关系来判断。
【课后巩固】
一、判断
1、直线与圆最多有两个公共点。 ( )
2、若C为⊙O上的一点,则过点C的直线与⊙O相切。( )
3、若A、B是⊙O外两点, 则直线AB与⊙O相离。 ( )
4、若C为⊙O内一点,则过点C的直线与⊙O相交。 ( )
二、填空
1、已知⊙O的半径为5cm,O到直线a的距离为3cm,则⊙O与直线a的位置关系是_____。直线a与⊙O的公共点个数是____。
2、已知⊙O的半径为6cm,O到直线a的距离为7cm,则直线a与⊙O的公共点个数是____。
3、已知⊙O的半径是4cm,O到直线a的距离是4cm,则⊙O与直线a的位置关系是 ___ _。
4、已知⊙O的直径是6cm,O到直线a的距离是4cm,则⊙O与直线a的位置关系是 ___ _。
5、⊙O半径为r,圆心O到直线l的距离为d,且d与r是方程x2-9x+20 =
0的两根,则直线l与⊙O的位置关系是 。
6、如图,已知∠AOB= 30°,M为OB上一点,且OM=5cm,若以M为圆心,r为半径作圆,那么:
1)当直线AB与⊙M相离时, r的取值范围是______________;
2)当直线AB与⊙M相切时, r的取值范围是______________;
3)当直线AB与⊙M有公共点时, r的取值范围是___________.
三、选择题
1.⊙O的半径为4,圆心O到直线l的距离为3,则直线l与⊙O的位置关系是( ) A.相交 B.相切 C.相离 D.无法确定
2、设⊙O的半径为4,点O到直线a的距离为d,若⊙O与直线a至多只有一个公共点,则d为…( )A、d≤4 B、d<4 C、d≥4 D、d=4
3、设⊙p的半径为4cm,直线l上一点A到圆心的距离为4cm,则直线l与⊙O的位置关系是( )A、相交 B、相切 C、相离 D、相切或相交
四、解答题
如图,已知Rt△ABC的斜边AB=8cm,AC=4cm.
(1)以点C为圆心作圆,当半径为多长时,直线AB与⊙C相切?为什么?
(2)以点C为圆心,分别以2cm和4cm为半径作两个圆,这两个圆与直线AB分别有怎样的位置关系?
学习目标:
1.了解直线和圆的位置关系的有关概念.
2.理解设⊙O的半径为r,直线L到圆心O的距离为d,则有:
直线L和⊙O相交 d
重点、难点
1、 重点:探索直线和圆的三种位置关系
2、 难点:探索直线和圆的三种位置关系及应用直线和圆的位置关系解决问题。
导学过程:阅读教材P93 —94 , 完成课前预习
【课前预习】
1:知识准备
点与圆的位置关系 数量关系
2:探究1:
(1)你看过日出吗?你知道太阳升起过程中,太阳和地平线会有几种不同位置关系吗?
(2)如图,在纸上画一条直线 L,把钥匙环看作一个圆,在纸上移动钥匙环,你能发现在钥匙环移动的过程中,它与直线L的公共点的个数吗?
发现:直线与圆有如下三种位置关系:
归纳:直线和圆有两个公共点,直线和圆 ,这条直线叫做圆的 .
直线和圆有一个公共点,直线和圆 ,这条直线叫做圆的 ,这个点叫做 .
直线和圆没有公共点,这条直线和圆 .
探究2: 设⊙O的半径为r,圆心到直线L的距离为d,在直线和圆的不同位置关系中,d和r具有怎样的大小关系?反过来,你能根据d和r的大小关系来确定直线和圆的位置关系吗?
(a) (b)
(c)
直线L和⊙O相交 d r,如图(a)所示;
直线L和⊙O相切 d r,如图(b)所示;
直线L和⊙O相离 d r,如图(c)所示.
【课堂活动】
活动1:预习反馈
活动2:典型例题
例1.圆的直径是13,如果直线与圆心的距离分别如下,判断直线与圆的位置关系?并说明公共点的个数.
⑴ 4.5 ⑵ 6.5 ⑶ 8
例2.在 Rt△ABC 中,∠C = 90°,AC = 3 cm , BC = 4 cm ,以 C 为圆心,下列r 为半径的圆与AB有怎样的位置关系?
⑴r=2cm ⑵r=2.4cm ⑶r=3cm
活动3:随堂训练
1.⊙O的半径是5,点O到直线l的距离为4,则直线l与⊙O的位置关系为( )
A.相离 B.相切 C.相交 D.相交或相切
2.如果⊙O的直径为6厘米,圆心O到直线AB的距离为5厘米,则直线与AB的位置关系为( )
A.相离 B.相切 C.相交 D.不确定
3、已知⊙O的直径为10.
(1)、若直线与⊙O相交,则圆心O到直线的距离d ________;
(2)、若直线与⊙O相切,则圆心O到直线的距离d ________;
(3)、若直线与⊙O相离,则圆心O到直线的距离d ________.
4、已知⊙A的直径为6,点A的坐标为(-3,-4),则⊙A与X轴的位置关系是_____,⊙A与Y轴的位置关系是______。
5、已知△ABC 中,AB=AC=5,BC=6,以点A为圆心,以4为半径作⊙A ,⊙A 与直线BC的位置关系怎样。
活动4:课堂小结
1、直线和圆的位置关系表:
直线和圆的位置关系 相交 相切 相离
公共点的个数
公共点名称
直线名称
圆心到直线的距离d与r的关系
2、确定直线与圆的位置关系的方法有____种
(1)根据定义,由___________ _______的个数来判断;
(2)根据性质,由_________________________ 的关系来判断。
【课后巩固】
一、判断
1、直线与圆最多有两个公共点。 ( )
2、若C为⊙O上的一点,则过点C的直线与⊙O相切。( )
3、若A、B是⊙O外两点, 则直线AB与⊙O相离。 ( )
4、若C为⊙O内一点,则过点C的直线与⊙O相交。 ( )
二、填空
1、已知⊙O的半径为5cm,O到直线a的距离为3cm,则⊙O与直线a的位置关系是_____。直线a与⊙O的公共点个数是____。
2、已知⊙O的半径为6cm,O到直线a的距离为7cm,则直线a与⊙O的公共点个数是____。
3、已知⊙O的半径是4cm,O到直线a的距离是4cm,则⊙O与直线a的位置关系是 ___ _。
4、已知⊙O的直径是6cm,O到直线a的距离是4cm,则⊙O与直线a的位置关系是 ___ _。
5、⊙O半径为r,圆心O到直线l的距离为d,且d与r是方程x2-9x+20 =
0的两根,则直线l与⊙O的位置关系是 。
6、如图,已知∠AOB= 30°,M为OB上一点,且OM=5cm,若以M为圆心,r为半径作圆,那么:
1)当直线AB与⊙M相离时, r的取值范围是______________;
2)当直线AB与⊙M相切时, r的取值范围是______________;
3)当直线AB与⊙M有公共点时, r的取值范围是___________.
三、选择题
1.⊙O的半径为4,圆心O到直线l的距离为3,则直线l与⊙O的位置关系是( ) A.相交 B.相切 C.相离 D.无法确定
2、设⊙O的半径为4,点O到直线a的距离为d,若⊙O与直线a至多只有一个公共点,则d为…( )A、d≤4 B、d<4 C、d≥4 D、d=4
3、设⊙p的半径为4cm,直线l上一点A到圆心的距离为4cm,则直线l与⊙O的位置关系是( )A、相交 B、相切 C、相离 D、相切或相交
四、解答题
如图,已知Rt△ABC的斜边AB=8cm,AC=4cm.
(1)以点C为圆心作圆,当半径为多长时,直线AB与⊙C相切?为什么?
(2)以点C为圆心,分别以2cm和4cm为半径作两个圆,这两个圆与直线AB分别有怎样的位置关系?
同课章节目录
