5.1.1 相交线 课件(共23张PPT)
文档属性
| 名称 | 5.1.1 相交线 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-19 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
人教版七年级数学下册
5.1.1 相交线
请你欣赏
大胆发现
我们日常生活中有哪些直线相交、平行的实际例子?
畅所欲言
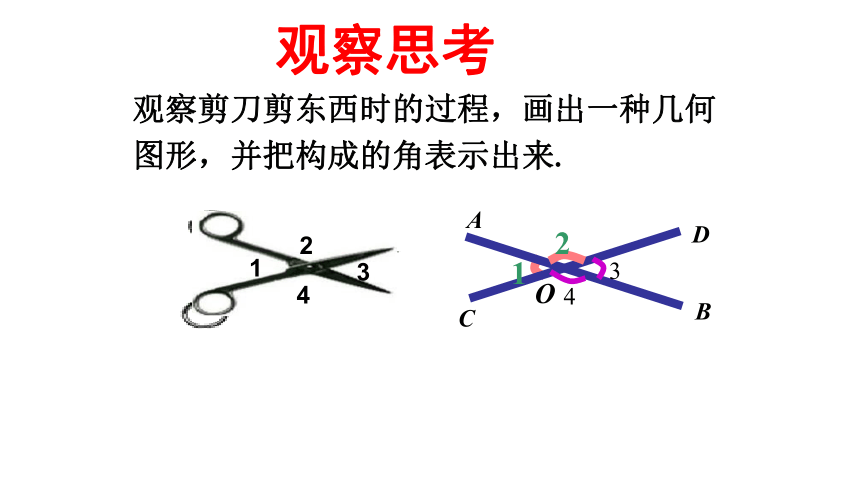
观察思考
请同学们观察张开的剪刀,画出相应的几何图形.
A
B
C
D
如果两条直线只有一个公共点,就说这两条直线相交.
该公共点叫做两直线的交点.
直线AB、CD相交于点O.
O
观察思考
观察剪刀剪东西时的过程,画出一种几何图形,并把构成的角表示出来.
1
2
A
C
D
O
3
4
B
3
4
2
1
问题1: ∠1 与∠2、∠2与∠3 、∠3与∠4、
∠4与∠1分别有何联系?
1.有一条公共边.
2.角的另一边互为反向延长线.
邻补角
探索交流
∠1= ∠3.
1
2
3
4
B
A
C
D
o
思 考
对顶角
1.顶点相同.
2.角的两边互为反向延长线.
对顶角是成对出现的
问题2: ∠1 与∠3、∠2与∠4 分别有何联系?
探索交流
1
2
3
4
B
A
C
D
o
初步练习1. 下列各图中∠1、∠2是对顶角吗?为什么?
2
1
2
1
2
)
(
(
1
初步练习2. 下列各图中∠1、∠2是邻补角吗?为什么?
2
1
2
1
2
)
(
(
(
)
(
1
)
(
)
探索交流
你能得到对顶角∠1和∠3的大小关系吗?
∠2与∠3互补,
∠1与∠2互补,
那么∠ 2 +∠1= ,
∠1= ∠3.
180°
180°
由同角的补角相等可知
动动脑:为什么?
∠ 2 +∠3= ,
1
2
3
4
B
A
C
D
o
对顶角的性质:
对顶角相等
例1 如图,直线a、b相交,∠1=40°,求
∠2、∠3、∠4的度数.
例题讲解
变式1:若∠1= 32°20′,求∠2、∠3、∠4的
度数.
解:由邻补角的定义可知
∠2=180°-∠1
=180°-40°=140°.
由对顶角相等可得
∠3=∠1=40°,∠4=∠2=140°.
2
)
1
)
(
3
4
(
1
1
)
a
b
(
3
4
(
解:设∠1=x°,则∠2=3x°.
变式3:若∠2是∠1的3倍,求∠3的度数.
根据邻补角的定义,得 x+3x=180°.
所以 x=45°,
根据对顶角相等,可得
∠3=∠1=45°.
则∠1=45°.
变式2:若∠1+∠3 = 50°,则∠3= ,
∠2= .
25°
155°
a
b
)
(
1
3
4
2
)
(
1.判 断
(1)对顶角相等. ( )
(2)相等的角是对顶角.( )
(3)若两个角不相等,则这两个角一定不是对顶
角. ( )
(4)若这两个角不是对顶角,则这两个角不相等. ( )
(5)有公共顶点,并且相等的角是对顶角.( )
(6)两条直线相交,有公共顶点的角是对顶角.( )
√
×
√
×
×
×
2.如图,三条直线相交于一点O,说出图中所有对顶角.
说 一 说
A
B
C
D
O
C
D
E
F
O
F
A
B
E
F
O
F
A
B
C
D
O
E
F
想一想
3. 图中是对顶角量角器,你能说出用它测量角的原理吗?
A
B
C
D
4. 如图,已知直线AD和BE相交
于点O, ∠ DOE与∠ COE互余,
∠ COE =52°,求∠ BOD的度数.
A
O
D
B
E
C
解:∵∠DOE与∠COE 互余,(已知)
∴ ∠DOE+ ∠COE =90°, (互余的意义)
∴ ∠DOE= 90° -∠COE= 90°-52°=38°.
∵ ∠BOD 与∠DOE互为邻补角,
∴ ∠BOD =180°-38°=142°.
练一练
5.已知:如图, ∠ 1=70°,OE平分
∠ AOC,求 ∠ EOC和 ∠ BOC的度数.
求一求
1
A
B
C
D
E
O
做一做
6.如图,三条直线AB、CD、EF相交于点O,求∠1+∠3+∠5等于多少度?
·还有什么疑问吗?
·你想进一步探究的问 题是什么?
·今天你有什么收获?
反思总结
2.举出生活中应用对顶角相等的例子.
3.习题5.1第1、2、7题.
1.阅读本节课的教材.
布置作业
人教版七年级数学下册
5.1.1 相交线
请你欣赏
大胆发现
我们日常生活中有哪些直线相交、平行的实际例子?
畅所欲言
观察思考
请同学们观察张开的剪刀,画出相应的几何图形.
A
B
C
D
如果两条直线只有一个公共点,就说这两条直线相交.
该公共点叫做两直线的交点.
直线AB、CD相交于点O.
O
观察思考
观察剪刀剪东西时的过程,画出一种几何图形,并把构成的角表示出来.
1
2
A
C
D
O
3
4
B
3
4
2
1
问题1: ∠1 与∠2、∠2与∠3 、∠3与∠4、
∠4与∠1分别有何联系?
1.有一条公共边.
2.角的另一边互为反向延长线.
邻补角
探索交流
∠1= ∠3.
1
2
3
4
B
A
C
D
o
思 考
对顶角
1.顶点相同.
2.角的两边互为反向延长线.
对顶角是成对出现的
问题2: ∠1 与∠3、∠2与∠4 分别有何联系?
探索交流
1
2
3
4
B
A
C
D
o
初步练习1. 下列各图中∠1、∠2是对顶角吗?为什么?
2
1
2
1
2
)
(
(
1
初步练习2. 下列各图中∠1、∠2是邻补角吗?为什么?
2
1
2
1
2
)
(
(
(
)
(
1
)
(
)
探索交流
你能得到对顶角∠1和∠3的大小关系吗?
∠2与∠3互补,
∠1与∠2互补,
那么∠ 2 +∠1= ,
∠1= ∠3.
180°
180°
由同角的补角相等可知
动动脑:为什么?
∠ 2 +∠3= ,
1
2
3
4
B
A
C
D
o
对顶角的性质:
对顶角相等
例1 如图,直线a、b相交,∠1=40°,求
∠2、∠3、∠4的度数.
例题讲解
变式1:若∠1= 32°20′,求∠2、∠3、∠4的
度数.
解:由邻补角的定义可知
∠2=180°-∠1
=180°-40°=140°.
由对顶角相等可得
∠3=∠1=40°,∠4=∠2=140°.
2
)
1
)
(
3
4
(
1
1
)
a
b
(
3
4
(
解:设∠1=x°,则∠2=3x°.
变式3:若∠2是∠1的3倍,求∠3的度数.
根据邻补角的定义,得 x+3x=180°.
所以 x=45°,
根据对顶角相等,可得
∠3=∠1=45°.
则∠1=45°.
变式2:若∠1+∠3 = 50°,则∠3= ,
∠2= .
25°
155°
a
b
)
(
1
3
4
2
)
(
1.判 断
(1)对顶角相等. ( )
(2)相等的角是对顶角.( )
(3)若两个角不相等,则这两个角一定不是对顶
角. ( )
(4)若这两个角不是对顶角,则这两个角不相等. ( )
(5)有公共顶点,并且相等的角是对顶角.( )
(6)两条直线相交,有公共顶点的角是对顶角.( )
√
×
√
×
×
×
2.如图,三条直线相交于一点O,说出图中所有对顶角.
说 一 说
A
B
C
D
O
C
D
E
F
O
F
A
B
E
F
O
F
A
B
C
D
O
E
F
想一想
3. 图中是对顶角量角器,你能说出用它测量角的原理吗?
A
B
C
D
4. 如图,已知直线AD和BE相交
于点O, ∠ DOE与∠ COE互余,
∠ COE =52°,求∠ BOD的度数.
A
O
D
B
E
C
解:∵∠DOE与∠COE 互余,(已知)
∴ ∠DOE+ ∠COE =90°, (互余的意义)
∴ ∠DOE= 90° -∠COE= 90°-52°=38°.
∵ ∠BOD 与∠DOE互为邻补角,
∴ ∠BOD =180°-38°=142°.
练一练
5.已知:如图, ∠ 1=70°,OE平分
∠ AOC,求 ∠ EOC和 ∠ BOC的度数.
求一求
1
A
B
C
D
E
O
做一做
6.如图,三条直线AB、CD、EF相交于点O,求∠1+∠3+∠5等于多少度?
·还有什么疑问吗?
·你想进一步探究的问 题是什么?
·今天你有什么收获?
反思总结
2.举出生活中应用对顶角相等的例子.
3.习题5.1第1、2、7题.
1.阅读本节课的教材.
布置作业
