13.1平方根(3)
图片预览








文档简介
课件23张PPT。13.1. 平方根(3)学习目标:
1、理解并识记平方根和开平方的概念
2、会正确的求一个非负数的平方根自 学 指 导:认真看课本P72——P75练习上面,注意:
(1)回答P72 思考 ”中的问题和填写P73表格,理解平方根和开平方的概念。
(2)想一想P74思考 ”和“云图” 里的问题,并填写归纳中的空白。
(3)例4、例5的格式和步骤,并思考平方根和算术平方根的区别和联系。
6分钟后,比谁能正确做对与例题类似的题。
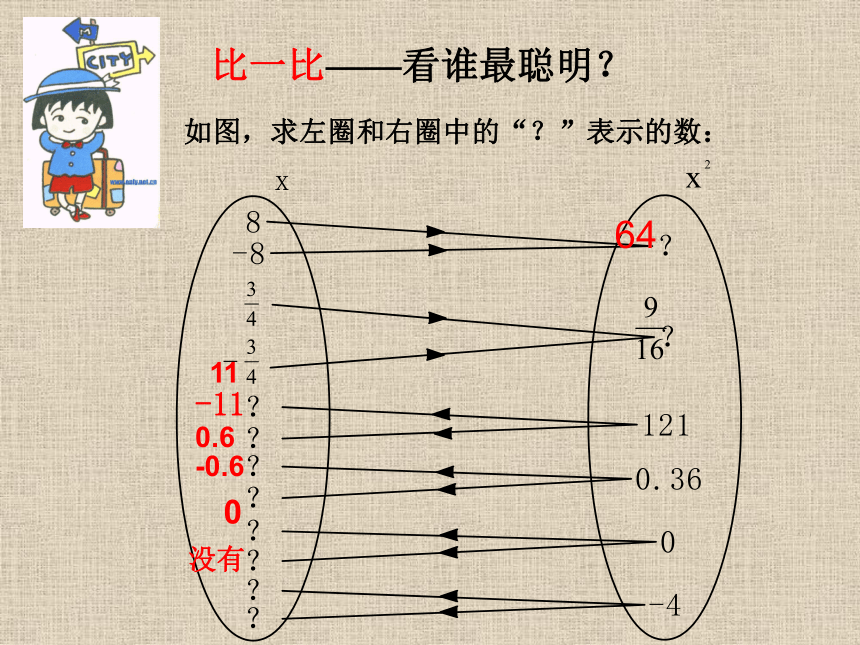
比一比——看谁最聪明? 如图,求左圈和右圈中的“?”表示的数: 64-11110.6-0.60没有 例4 求下列各数的平方根。
(1) 100 (2) (3) 0.25
1、平方根的概念:如果一个数的平方等于a,
那么这个数就叫做a的___________或 _______.
即:如果=a,那么x叫做_____________.求一个数的平方根的运算,叫做_______.例如±3的平方等于9,9的平方根是±3,
所以平方与开平方互为逆运算.平方根二次方根a的平方根开平方平方根的表示法: (5)一个正数有两个平方根,它们互为相反数.
零的平方根是零.
负数没有平方根.区别:
1.定义不同; 2.个数不同;
3.表示法不同; 4.取值范围不同.平方根与算术平方根的联系与区别:联系:
1.算术平方根是平方根的一种;
2.只有非负数才有算术平方根和平方根;
3.0的算术平方根和平方根都是0.例:求下列各式的值。
(1)(2)-(3) (4)(5)3、按照平方根的概念,思考并讨论下列问题:
正数的平方根有什么特点?0的平方根是多少?
负数有平方根吗?归纳:正数有 个平方根,它们 。
0的平方根是 ,负数 。
注意:正数有两个平方根,即正数进行开平方运
算有两个结果,负数没有平方根,即负数不能进
行开平方运算,符号:正数a的算术平方根可用
表示;正数a的负的平方根可用- 表示。两个互为相反数0没有平方根自 学 检 测一、自 学 检 测
4、求下列各数的平方根.
(1)0.49 (2) (3)81 (4)0 (5)-100 解:(1)因为0.72=0.49,(-0.7)2=0.49,
所以0.49的平方根为±0.7,即± = ±0.7 (3)因为92=81,(-9)2=81,所以81的平方根为±9,
即±=±9. (4)因为02=0,所以0的平方根为0,即± = 0(5)因为任何数的平方都不小于0,找不到平方
为-100的数,故-100没有平方根. 1.(-8)2的平方根是____,算术平方根是____;±88±33±74.若(x-2)2=36,则x=__________;±98或-4自 学 检 测二a 若a是正数,则等于a;若a是负数,则等于-a;若a是0,则等于0DD9.已知(2x)2=36,y是(-5)2的正的平方根,求代数 式5x-3y的值.10.一个数的两个平方根分别是 3a+2 与
5a-10,求这个数. 解:因为一个数的平方根互为相反数,
所以,
(3a+2)+(5a-10)=0
所以 a=1.5、如果一个正数的一个平方根为4,则另一个平
方根为多少?6. 已知,求:根的平方根解:因为一个正数的平方根有两个,它
们互为相反数,所以另一个平方根为-4{解:由题意,得 3a-b-7=0
2a+b-3=0解得: a=2
b=-1{注意平方根的表示方法7、如果一个正数的两个平方根为和,请你求出这个正数
(1)8、求下列各式中的x解:由题意,得 (a+1)+(2a-7)=0
解得: a=2
所以a+13也可救出2a-7,
再求它的平方=注意:是求平方根四、小结:1、什么叫做一个数的平方根?
2、正数、0、负数的平方根有什么规律?3、怎样求出一个数的平方根?数a的平方怎
样表示?五、作业 P75-76习题13.1
第3、4、7、8、10、11、12题。当堂训练必做题 P56 6。
P57 7。
选做题 P58 14
再 见
2、会正确的求一个非负数的平方根自 学 指 导:认真看课本P72——P75练习上面,注意:
(1)回答P72 思考 ”中的问题和填写P73表格,理解平方根和开平方的概念。
(2)想一想P74思考 ”和“云图” 里的问题,并填写归纳中的空白。
(3)例4、例5的格式和步骤,并思考平方根和算术平方根的区别和联系。
6分钟后,比谁能正确做对与例题类似的题。
比一比——看谁最聪明? 如图,求左圈和右圈中的“?”表示的数: 64-11110.6-0.60没有 例4 求下列各数的平方根。
(1) 100 (2) (3) 0.25
1、平方根的概念:如果一个数的平方等于a,
那么这个数就叫做a的___________或 _______.
即:如果=a,那么x叫做_____________.求一个数的平方根的运算,叫做_______.例如±3的平方等于9,9的平方根是±3,
所以平方与开平方互为逆运算.平方根二次方根a的平方根开平方平方根的表示法: (5)一个正数有两个平方根,它们互为相反数.
零的平方根是零.
负数没有平方根.区别:
1.定义不同; 2.个数不同;
3.表示法不同; 4.取值范围不同.平方根与算术平方根的联系与区别:联系:
1.算术平方根是平方根的一种;
2.只有非负数才有算术平方根和平方根;
3.0的算术平方根和平方根都是0.例:求下列各式的值。
(1)(2)-(3) (4)(5)3、按照平方根的概念,思考并讨论下列问题:
正数的平方根有什么特点?0的平方根是多少?
负数有平方根吗?归纳:正数有 个平方根,它们 。
0的平方根是 ,负数 。
注意:正数有两个平方根,即正数进行开平方运
算有两个结果,负数没有平方根,即负数不能进
行开平方运算,符号:正数a的算术平方根可用
表示;正数a的负的平方根可用- 表示。两个互为相反数0没有平方根自 学 检 测一、自 学 检 测
4、求下列各数的平方根.
(1)0.49 (2) (3)81 (4)0 (5)-100 解:(1)因为0.72=0.49,(-0.7)2=0.49,
所以0.49的平方根为±0.7,即± = ±0.7 (3)因为92=81,(-9)2=81,所以81的平方根为±9,
即±=±9. (4)因为02=0,所以0的平方根为0,即± = 0(5)因为任何数的平方都不小于0,找不到平方
为-100的数,故-100没有平方根. 1.(-8)2的平方根是____,算术平方根是____;±88±33±74.若(x-2)2=36,则x=__________;±98或-4自 学 检 测二a 若a是正数,则等于a;若a是负数,则等于-a;若a是0,则等于0DD9.已知(2x)2=36,y是(-5)2的正的平方根,求代数 式5x-3y的值.10.一个数的两个平方根分别是 3a+2 与
5a-10,求这个数. 解:因为一个数的平方根互为相反数,
所以,
(3a+2)+(5a-10)=0
所以 a=1.5、如果一个正数的一个平方根为4,则另一个平
方根为多少?6. 已知,求:根的平方根解:因为一个正数的平方根有两个,它
们互为相反数,所以另一个平方根为-4{解:由题意,得 3a-b-7=0
2a+b-3=0解得: a=2
b=-1{注意平方根的表示方法7、如果一个正数的两个平方根为和,请你求出这个正数
(1)8、求下列各式中的x解:由题意,得 (a+1)+(2a-7)=0
解得: a=2
所以a+13也可救出2a-7,
再求它的平方=注意:是求平方根四、小结:1、什么叫做一个数的平方根?
2、正数、0、负数的平方根有什么规律?3、怎样求出一个数的平方根?数a的平方怎
样表示?五、作业 P75-76习题13.1
第3、4、7、8、10、11、12题。当堂训练必做题 P56 6。
P57 7。
选做题 P58 14
再 见
