双曲线的简单几何性质
图片预览







文档简介
课件40张PPT。 2.3.2 双曲线的
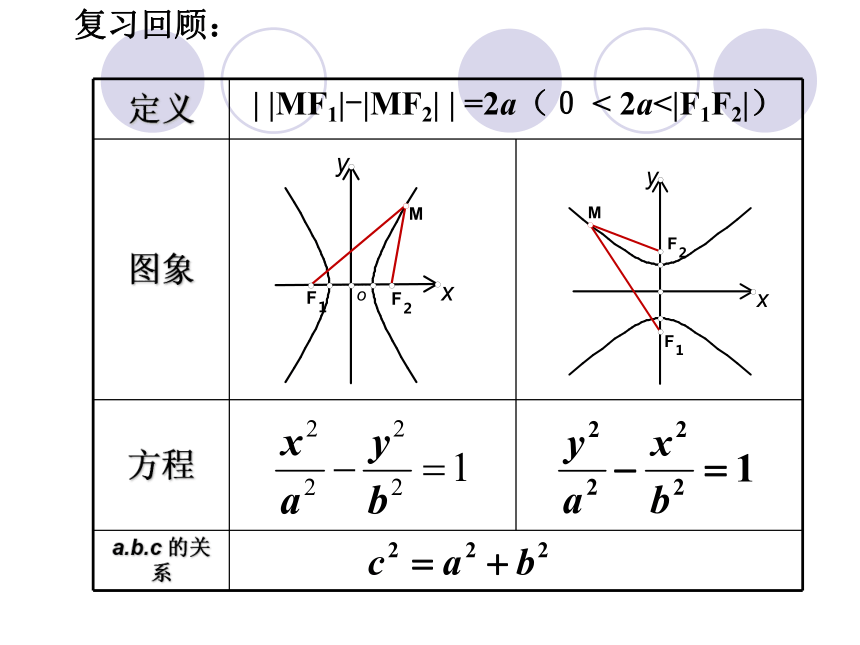
简单几何性质| |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)复习回顾:oYX关于X,Y轴,
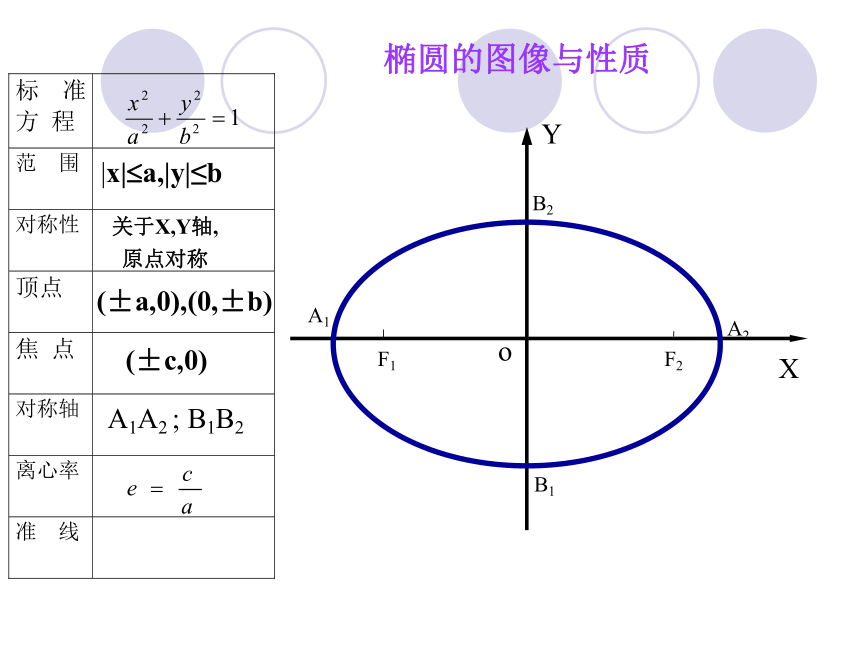
原点对称(±a,0),(0,±b)(±c,0)A1A2 ; B1B2|x|?a,|y|≤b
F1F2A1A2B2B1椭圆的图像与性质范围、对称性、顶点、离心率.渐近线类比椭圆,探讨双曲线
的几何性质:x轴、y轴是双曲线的对称轴,原点是对称中心,
又叫做双曲线的中心。
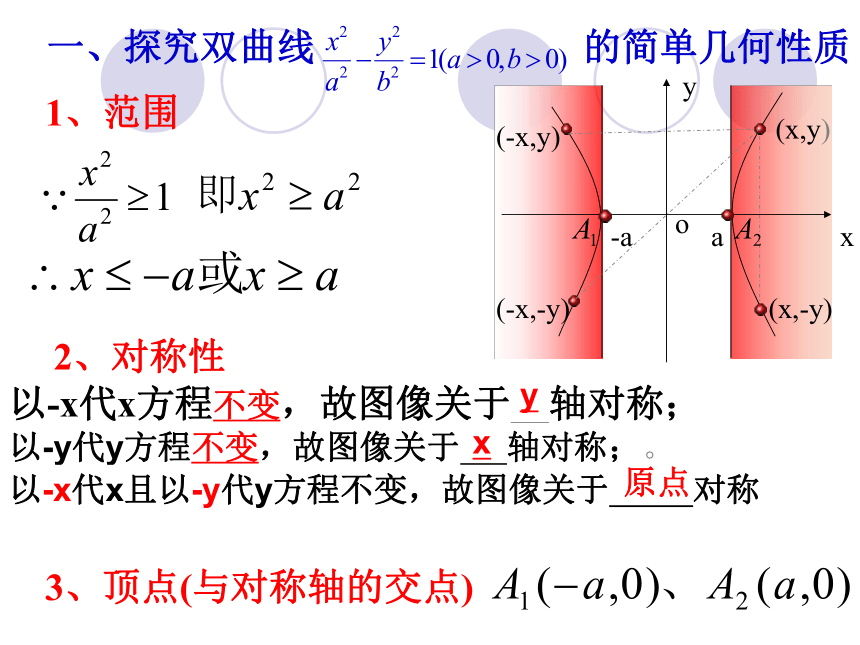
2、对称性 一、探究双曲线 的简单几何性质1、范围以-x代x方程不变,故图像关于 轴对称;
(-x,-y)(-x,y)(x,y)(x,-y)3、顶点(与对称轴的交点)以-y代y方程不变,故图像关于 轴对称;。以-x代x且以-y代y方程不变,故图像关于 对称yx原点3、顶点(1)双曲线与对称轴的交点,叫做双曲线的顶点如图,线段 叫做双曲线的实轴,它的长为2a,a叫做实半轴长;
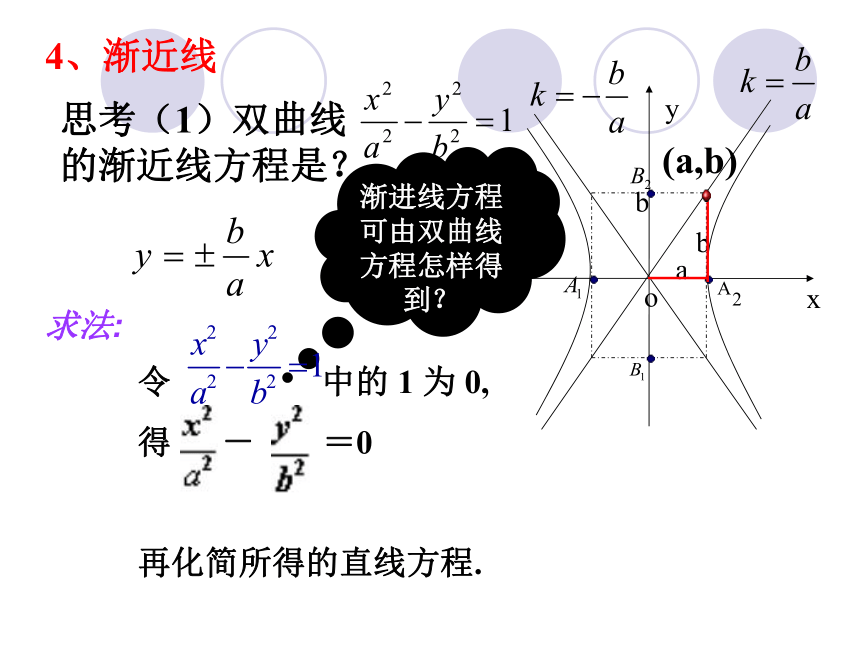
线段 叫做双曲线的虚轴,它的长为2b,b叫做双曲线的虚半轴长(2)4、渐近线xyoab思考(1)双曲线 的渐近线方程是?渐进线方程可由双曲线方程怎样得到?b(a,b)令 中的 1 为 0,
得 - =0
再化简所得的直线方程.求法:
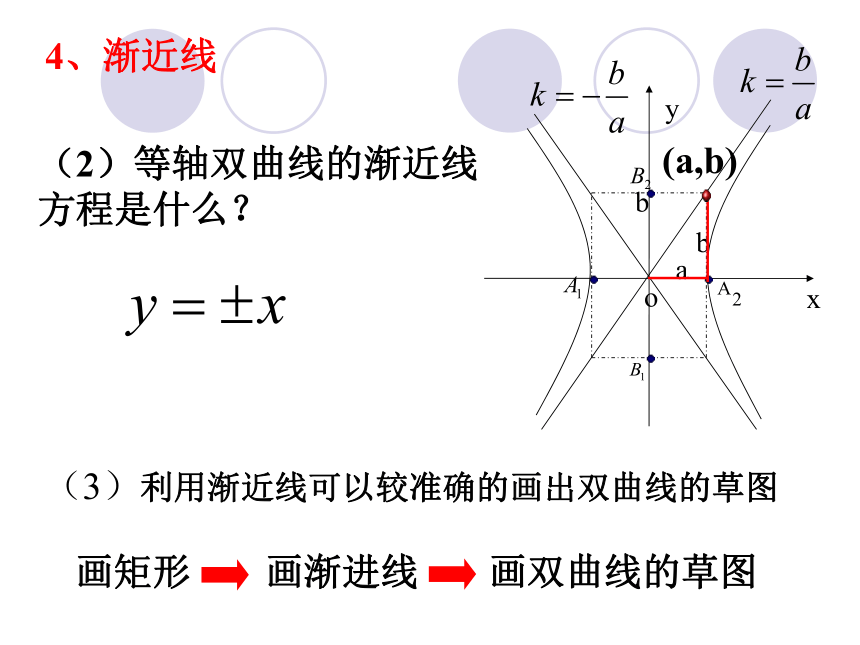
名师点睛4、渐近线xyoab(3)利用渐近线可以较准确的画出双曲线的草图(2)等轴双曲线的渐近线方程是什么?b(a,b)画矩形画渐进线画双曲线的草图【例2】 题型二 根据双曲线的几何性质求标准方程【变式2】5、离心率e是表示双曲线开口大小的一个量,e越大开口越大等轴双曲线的离心率e= ?
名师点睛| |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)双曲线定义的简单几何性质(0,-a) (0, a)
(-a, 0) (a, 0)
x≤-a或x≥a
y≤-a或y≥a关于坐标轴、原点对称(实轴、虚轴、中心)y= ± x ( ± = 0)双曲线的几何性质
自学导引续表F1(-c,0)、F2(c,0)F1(0,-c)、F2(0,c)|F1F2|=2cA1(-a,0)、A2(a,0)A1(0,-a)、A2(0,a)2a2b关于x轴、y轴、原点对称图形方程范围对称性顶点离心率A1(- a,0),A2(a,0)B1(0,-b),B2(0,b)F1(-c,0) F2(c,0)关于x轴、y轴、原点对称A1(- a,0),A2(a,0)渐进线无例3: 1、双曲线 9x2-16y2=144的实半轴长等于 虚半轴长等于 顶点坐
标是 渐近线方是 .
离心率e= 。432、离心率e= 是双曲线为等轴双曲线的
条件 。(用“充分条件”“必要条件”“充要条件”填空。) 充要课本 61页 练习 1(1)(3)课本 61页 练习 2解:xy..FO.M.例5、点M(x,y)与定点F(5,0)的距离和它到定直线 的距离的比是常数 ,求点M的轨迹。双曲线的第二定义:x课本 61页 练习 3课本 61页 练习 4例6:如图所示,过双曲线 的右焦点F2,倾斜角为
30°的直线交双曲线于A,B两点,求|AB|AB例6:如图所示,过双曲线 的右焦点F2,倾斜角为
30°的直线交双曲线于A,B两点,求|AB|AB*活页规范训练1.双曲线mx2+y2=1的虚轴长是实轴长的2倍,则m的值为 ( ).
A.- B.-4 C.4 D.
解析 由双曲线方程mx2+y2=1,知m<0,则双曲
线方程可化为 ,则a2=1,
a=1,又虚轴长是实轴长的2倍,∴b=2,
∴ ,∴m=- ,故选A.
答案 A2.双曲线3x2-y2=3的渐近线方程是 ( ).
A.y=±3x B.y=± x
C.y=± x D.y=± x
解析 令 ,则y=± x.
答案 C3.已知中心在原点,对称轴为坐标轴且经过点P(1,3),离心率为的双曲线的标准方程为 ( ).
A. B.
C. D
解析 由离心率为 ,
∴e2 ,即a=b,
∴双曲线为等轴双曲线,故设所求双曲线的标准方程为x2-y2=λ(λ≠0),又点P(1,3)
在双曲线上,则λ=1-9=-8,
∴所求双曲线的标准方程为 .故选D.
答案 D4.与双曲线 有共同的渐近线,且过点(2,2)的双曲线的标准方程是________.
解析 依题意设双曲线的方程
x2- =λ(λ≠0),
将点(2,2)代入求得λ=3,
所以所求双曲线的标准方程为
.
答案
名师点睛7.在平面直角坐标系xOy中,双曲线的中心在坐标原点,焦点在y轴上, 一条渐近线的方程为x-2y=0,则它的离心率为 ( ).
A. B. C. D.2
解析 由题意知,这条渐近线的斜率为 ,
即 ,
而e ,故选A.
答案 A10.过双曲线的一个焦点F2作垂直于实轴的弦PQ,点F1是另一个焦点,若∠PF1Q=90°,则双曲线的离心率等于________.
解析 设F1、F2分别是双曲线的左、右焦点,由题意知在焦点三角形F1PF2中,
|PF1|=2 c,|PF2|=2c,
又|PF1|-|PF2|=2a,故有e= +1.
答案 +1
简单几何性质| |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)复习回顾:oYX关于X,Y轴,
原点对称(±a,0),(0,±b)(±c,0)A1A2 ; B1B2|x|?a,|y|≤b
F1F2A1A2B2B1椭圆的图像与性质范围、对称性、顶点、离心率.渐近线类比椭圆,探讨双曲线
的几何性质:x轴、y轴是双曲线的对称轴,原点是对称中心,
又叫做双曲线的中心。
2、对称性 一、探究双曲线 的简单几何性质1、范围以-x代x方程不变,故图像关于 轴对称;
(-x,-y)(-x,y)(x,y)(x,-y)3、顶点(与对称轴的交点)以-y代y方程不变,故图像关于 轴对称;。以-x代x且以-y代y方程不变,故图像关于 对称yx原点3、顶点(1)双曲线与对称轴的交点,叫做双曲线的顶点如图,线段 叫做双曲线的实轴,它的长为2a,a叫做实半轴长;
线段 叫做双曲线的虚轴,它的长为2b,b叫做双曲线的虚半轴长(2)4、渐近线xyoab思考(1)双曲线 的渐近线方程是?渐进线方程可由双曲线方程怎样得到?b(a,b)令 中的 1 为 0,
得 - =0
再化简所得的直线方程.求法:
名师点睛4、渐近线xyoab(3)利用渐近线可以较准确的画出双曲线的草图(2)等轴双曲线的渐近线方程是什么?b(a,b)画矩形画渐进线画双曲线的草图【例2】 题型二 根据双曲线的几何性质求标准方程【变式2】5、离心率e是表示双曲线开口大小的一个量,e越大开口越大等轴双曲线的离心率e= ?
名师点睛| |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)双曲线定义的简单几何性质(0,-a) (0, a)
(-a, 0) (a, 0)
x≤-a或x≥a
y≤-a或y≥a关于坐标轴、原点对称(实轴、虚轴、中心)y= ± x ( ± = 0)双曲线的几何性质
自学导引续表F1(-c,0)、F2(c,0)F1(0,-c)、F2(0,c)|F1F2|=2cA1(-a,0)、A2(a,0)A1(0,-a)、A2(0,a)2a2b关于x轴、y轴、原点对称图形方程范围对称性顶点离心率A1(- a,0),A2(a,0)B1(0,-b),B2(0,b)F1(-c,0) F2(c,0)关于x轴、y轴、原点对称A1(- a,0),A2(a,0)渐进线无例3: 1、双曲线 9x2-16y2=144的实半轴长等于 虚半轴长等于 顶点坐
标是 渐近线方是 .
离心率e= 。432、离心率e= 是双曲线为等轴双曲线的
条件 。(用“充分条件”“必要条件”“充要条件”填空。) 充要课本 61页 练习 1(1)(3)课本 61页 练习 2解:xy..FO.M.例5、点M(x,y)与定点F(5,0)的距离和它到定直线 的距离的比是常数 ,求点M的轨迹。双曲线的第二定义:x课本 61页 练习 3课本 61页 练习 4例6:如图所示,过双曲线 的右焦点F2,倾斜角为
30°的直线交双曲线于A,B两点,求|AB|AB例6:如图所示,过双曲线 的右焦点F2,倾斜角为
30°的直线交双曲线于A,B两点,求|AB|AB*活页规范训练1.双曲线mx2+y2=1的虚轴长是实轴长的2倍,则m的值为 ( ).
A.- B.-4 C.4 D.
解析 由双曲线方程mx2+y2=1,知m<0,则双曲
线方程可化为 ,则a2=1,
a=1,又虚轴长是实轴长的2倍,∴b=2,
∴ ,∴m=- ,故选A.
答案 A2.双曲线3x2-y2=3的渐近线方程是 ( ).
A.y=±3x B.y=± x
C.y=± x D.y=± x
解析 令 ,则y=± x.
答案 C3.已知中心在原点,对称轴为坐标轴且经过点P(1,3),离心率为的双曲线的标准方程为 ( ).
A. B.
C. D
解析 由离心率为 ,
∴e2 ,即a=b,
∴双曲线为等轴双曲线,故设所求双曲线的标准方程为x2-y2=λ(λ≠0),又点P(1,3)
在双曲线上,则λ=1-9=-8,
∴所求双曲线的标准方程为 .故选D.
答案 D4.与双曲线 有共同的渐近线,且过点(2,2)的双曲线的标准方程是________.
解析 依题意设双曲线的方程
x2- =λ(λ≠0),
将点(2,2)代入求得λ=3,
所以所求双曲线的标准方程为
.
答案
名师点睛7.在平面直角坐标系xOy中,双曲线的中心在坐标原点,焦点在y轴上, 一条渐近线的方程为x-2y=0,则它的离心率为 ( ).
A. B. C. D.2
解析 由题意知,这条渐近线的斜率为 ,
即 ,
而e ,故选A.
答案 A10.过双曲线的一个焦点F2作垂直于实轴的弦PQ,点F1是另一个焦点,若∠PF1Q=90°,则双曲线的离心率等于________.
解析 设F1、F2分别是双曲线的左、右焦点,由题意知在焦点三角形F1PF2中,
|PF1|=2 c,|PF2|=2c,
又|PF1|-|PF2|=2a,故有e= +1.
答案 +1
