北师大版七年级数学下册 1.5 平方差公式的应用 课件(共25张PPT)
文档属性
| 名称 | 北师大版七年级数学下册 1.5 平方差公式的应用 课件(共25张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 283.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-20 16:50:06 | ||
图片预览

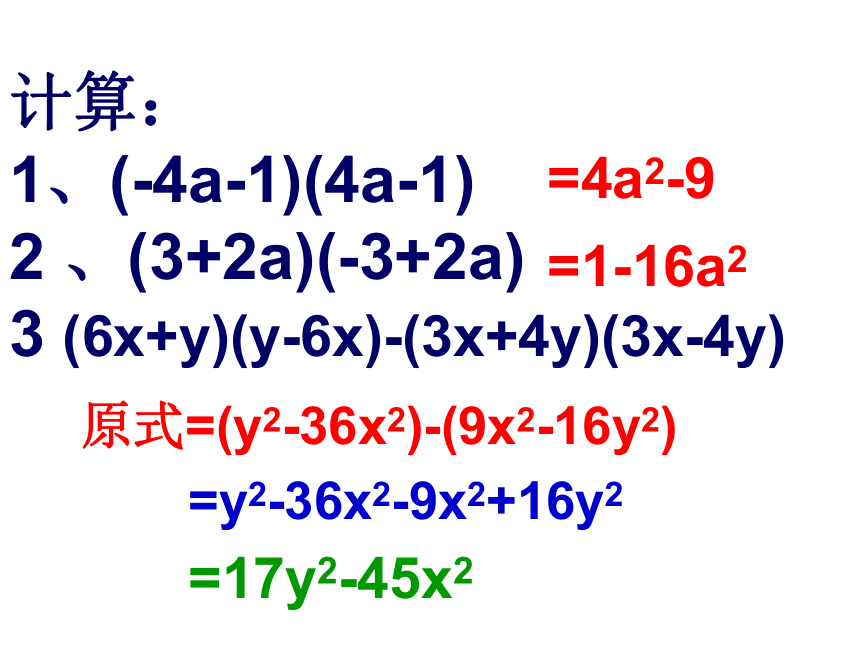






文档简介
(共25张PPT)
平方差公式的应用
计算:
1、(-4a-1)(4a-1)
2 、(3+2a)(-3+2a)
3 (6x+y)(y-6x)-(3x+4y)(3x-4y)
=17y2-45x2
原式=(y2-36x2)-(9x2-16y2)
=y2-36x2-9x2+16y2
=1-16a2
=4a2-9
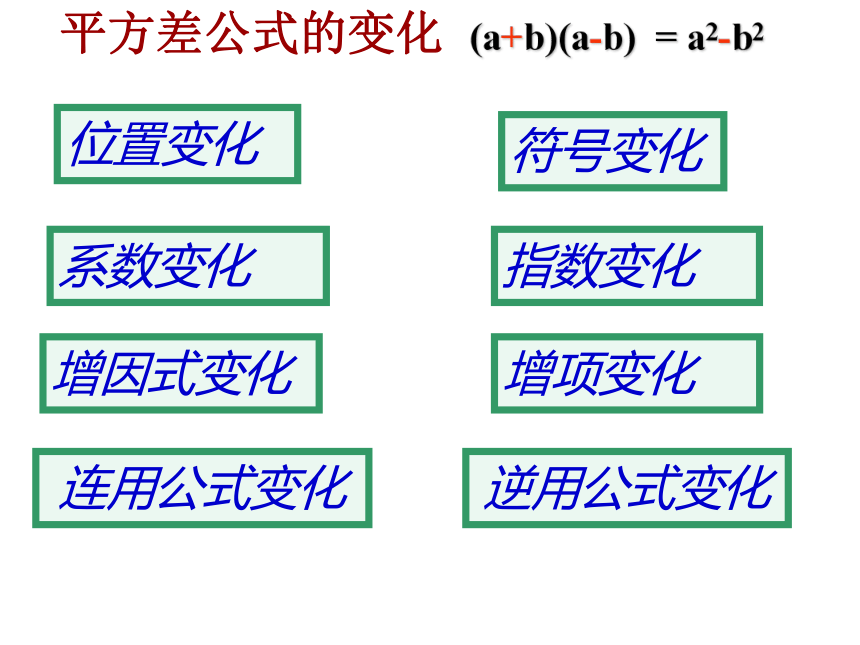
位置变化
符号变化
系数变化
指数变化
增因式变化
增项变化
连用公式变化
逆用公式变化
平方差公式的变化 (a+b)(a-b) = a2-b2
①位置变化
平方差公式
②符号变化
平方差公式
③系数变化
平方差公式
④指数变化
平方差公式
⑤增因式变化如
平方差公式
(x+y)(x-y)(-x-y)(-x+y)
=(x2-y2)[ (-x)2-y2 ]
=(x2-y2)(x2-y2)
=x4-2x2y2+y4
⑥增项变化
平方差公式
⑦连用公式变化
平方差公式
(x+y)(x-y)(x2+y2)
=(x2-y2)(x2+y2)
=x4-y4
平方差公式
⑧逆用公式变化
应用平方差公式 时要注意一些什么?
1运用平方差公式时,要紧扣公式的特征,找出相等的“项”和符号相反的“项”,然后应用公式
2对于不符合平方差公式标准形式者,要利用加法交换律,或提取两“ ”号中的“ ”号,变成公式标准形式后,再用公式。
一连续使用
例计算
1) (x+y)(x2+y2)(x4+y4)(x-y)
2) (x+3) (x-3) (x2+9) (x4+81)
3)(a+1)(a-1)( +1)( +1)( +1).
二变形后使用
(1) (a+2b+c)(a+2b-c)
(2)、(a+b-c) (a-b+c)
(3)已知:(m+35) 2=13302921,
求 (m+45)(m+25)的值。
练习1.[x+(y+1)] [x-(y+1)]
2.(a+b+c) (a+b-c)
=x2-y2-2y-1
=a2+2ab+b2-c2
=x2-(y+1)2
=x2-(y2+2y+1)
=[(a+b)+c][(a+b)-c]
=(a+b)2-c2
3.(2a-b)(4a2 +b2)(2a+b)
=(2a-b)(2a+b)(4a2+b2)
=(4a2-b2)(4a2+b2)
=16a4-b4
=a8-256
4.(a+2)(a2+4)(a4+16)(a-2)
.活动三
对于任意的正整数n,
整式(3n+1)(3n-1)-(3-n)(3+n)
的值一定是10的倍数吗?试说明理由
原式=(9n2-1)-(9-n2)
=9n2-1-9+n2
=10n2-10
=10(n2-1)
=-1
=2007
=1
解方程:
9x(x+2)-(2x+1)(2x-1)=5(x2+3)
三课标新型题
规律探索研究:(1-x)(1+x)=1-x2
(1-x)(1+x+x2)=1-x3
(1-x)(1+x+x2+x3)=1-x4
(1)观察以上各式并猜想
(1-x)(1+x+x2+x3+x4+……+xn)=____
(2)根据你的猜想计算
1、(1-2)(1+2+22+23+24+25)=______
2、2+22+23+24+25+…+2n=______
3、(x-1)(x99+x98+x97+…+x2+x+1)=____
1-xn+1
1-26
2n+1-2
X100-1
通过以上的规律请你进行下面的探索
(a-b)(a+b)=_____
(a-b)(a2+ab+b2)=__________
(a- b)(a3+a2b+ab2+b3)=_______
a2-b2
a3-b3
a4-b4
平方差公式的应用
计算:
1、(-4a-1)(4a-1)
2 、(3+2a)(-3+2a)
3 (6x+y)(y-6x)-(3x+4y)(3x-4y)
=17y2-45x2
原式=(y2-36x2)-(9x2-16y2)
=y2-36x2-9x2+16y2
=1-16a2
=4a2-9
位置变化
符号变化
系数变化
指数变化
增因式变化
增项变化
连用公式变化
逆用公式变化
平方差公式的变化 (a+b)(a-b) = a2-b2
①位置变化
平方差公式
②符号变化
平方差公式
③系数变化
平方差公式
④指数变化
平方差公式
⑤增因式变化如
平方差公式
(x+y)(x-y)(-x-y)(-x+y)
=(x2-y2)[ (-x)2-y2 ]
=(x2-y2)(x2-y2)
=x4-2x2y2+y4
⑥增项变化
平方差公式
⑦连用公式变化
平方差公式
(x+y)(x-y)(x2+y2)
=(x2-y2)(x2+y2)
=x4-y4
平方差公式
⑧逆用公式变化
应用平方差公式 时要注意一些什么?
1运用平方差公式时,要紧扣公式的特征,找出相等的“项”和符号相反的“项”,然后应用公式
2对于不符合平方差公式标准形式者,要利用加法交换律,或提取两“ ”号中的“ ”号,变成公式标准形式后,再用公式。
一连续使用
例计算
1) (x+y)(x2+y2)(x4+y4)(x-y)
2) (x+3) (x-3) (x2+9) (x4+81)
3)(a+1)(a-1)( +1)( +1)( +1).
二变形后使用
(1) (a+2b+c)(a+2b-c)
(2)、(a+b-c) (a-b+c)
(3)已知:(m+35) 2=13302921,
求 (m+45)(m+25)的值。
练习1.[x+(y+1)] [x-(y+1)]
2.(a+b+c) (a+b-c)
=x2-y2-2y-1
=a2+2ab+b2-c2
=x2-(y+1)2
=x2-(y2+2y+1)
=[(a+b)+c][(a+b)-c]
=(a+b)2-c2
3.(2a-b)(4a2 +b2)(2a+b)
=(2a-b)(2a+b)(4a2+b2)
=(4a2-b2)(4a2+b2)
=16a4-b4
=a8-256
4.(a+2)(a2+4)(a4+16)(a-2)
.活动三
对于任意的正整数n,
整式(3n+1)(3n-1)-(3-n)(3+n)
的值一定是10的倍数吗?试说明理由
原式=(9n2-1)-(9-n2)
=9n2-1-9+n2
=10n2-10
=10(n2-1)
=-1
=2007
=1
解方程:
9x(x+2)-(2x+1)(2x-1)=5(x2+3)
三课标新型题
规律探索研究:(1-x)(1+x)=1-x2
(1-x)(1+x+x2)=1-x3
(1-x)(1+x+x2+x3)=1-x4
(1)观察以上各式并猜想
(1-x)(1+x+x2+x3+x4+……+xn)=____
(2)根据你的猜想计算
1、(1-2)(1+2+22+23+24+25)=______
2、2+22+23+24+25+…+2n=______
3、(x-1)(x99+x98+x97+…+x2+x+1)=____
1-xn+1
1-26
2n+1-2
X100-1
通过以上的规律请你进行下面的探索
(a-b)(a+b)=_____
(a-b)(a2+ab+b2)=__________
(a- b)(a3+a2b+ab2+b3)=_______
a2-b2
a3-b3
a4-b4
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
