六年级数学上册课件 - 五 圆的周长 青岛版(共22张PPT)
文档属性
| 名称 | 六年级数学上册课件 - 五 圆的周长 青岛版(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-19 21:21:50 | ||
图片预览







文档简介
(共22张PPT)
圆的周长
青岛版六年级上册
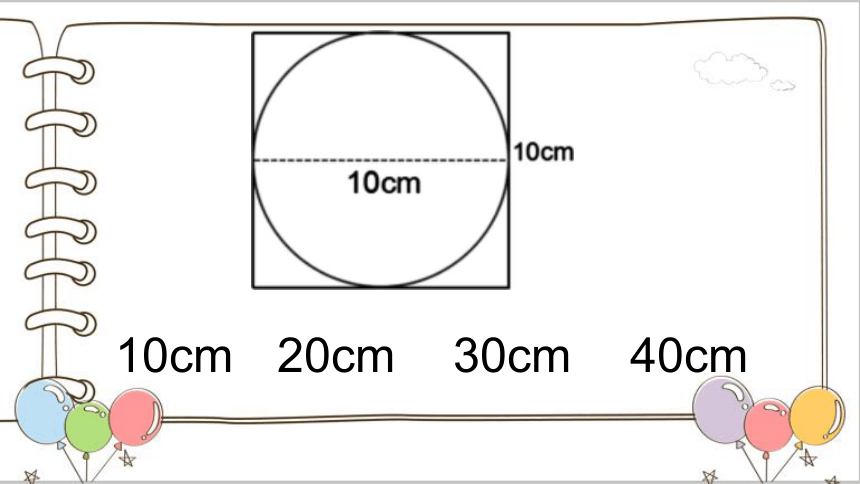
围成圆的曲线的长叫做圆的周长
10cm
20cm
30cm
40cm
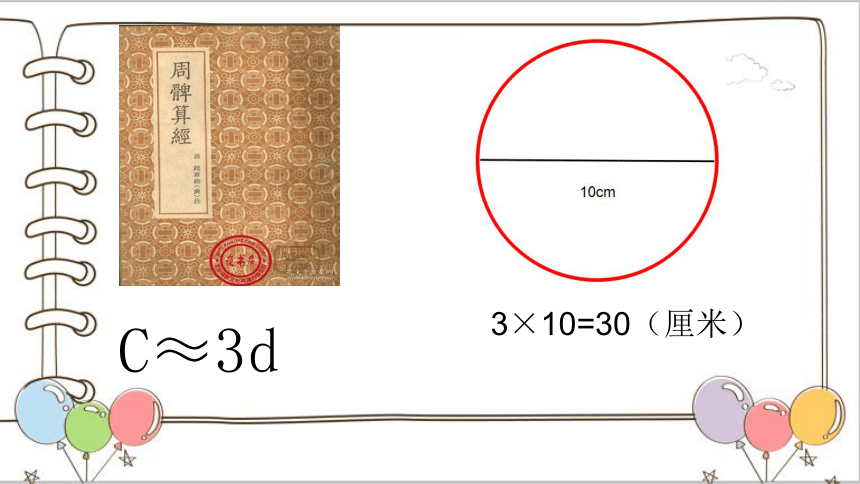
C=3d
周三径一
若想研究“周三径一”的说法是否正确,应该如何做?
研究“周三径一”是否正确
圆 直径(厘米) 若“周三径一 ”正确,周长为(厘米) 实际测量得到周长为(厘米) 研究结论
A
B
C
4
5
6
12
15
18
活动要求:
1.同桌两人一组,用合适的方法相互配合测量圆的周长。(测量结果保留一位小数)
2.在研究问题的时候,尽量不要有成见,客观真实地记录数据。
研究“周三径一”是否正确
圆 直径(厘米) 若“周三径一 ”正确,周长为(厘米) 实际测量得到周长为(厘米) 研究结论
A
B
C
4
5
6
12
15
18
C≈3d
3×10=30(厘米)
刘徽在《九章算术注》中提出了“割圆术”,并用割圆术将“3”改进成了“3.14”。刘徽在割圆中提出“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体,而无所失矣”。
刘徽
“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体,而无所失矣”
割圆术
刘徽
C≈3.14d
3.14×10=31.4(厘米)
祖冲之
隨书律历志
将“3.14”进一步改进为3.1415926到3.1415927之间。
祖冲之
C≈3.1415927d
3.1415927×10=
31.415927(厘米)
《周髀算经》
刘徽
祖冲之
后来……
C≈3d
C≈3.14d
C≈3.1415927d
C≈3.1415926……×d
圆的周长和它的直径的比值是一个固定的数,这个比值叫做圆周率,用希腊字母π(读作pài)表示。圆周率是一个无限不循环的小数,在实际应用中我们一般取它的近似值,即π≈3.14。
2016年瑞士物理学家用一台配置24个6 TB硬盘的电脑,花了105天,计算到圆周率小数点后的第22.4万亿位。2020年在3月14日,也就是国际圆周率这天,谷歌工程师利用谷歌云计算资源,花了121天,成功将圆周率π计算到小数点后31.4万亿位,刷新了世界纪录。假设一秒读一位的,一个人不分昼夜的读完这些天文般的数字,要花99万多年,若将它们全部写在厚0.1毫米的纸上,每张纸上写一万位,这些纸堆起来将比31座珠穆朗玛峰还高。
一、填空
1、《周髀算经》提出了___________的说法。
2、______在《九章算术注》采用________将 3 改进成了3.14.
3、_________计算是世界上第一个把圆周率的值精确到七位小数的人
4、世界圆周率日是___________
周三径一
刘徽
割圆术
祖冲之
3月14日
1、两个圆的周长相等,那么这两个圆的直径也相等。 ( )
√
×
√
3、 π=3.14 ( )
2、圆的直径扩大a倍,那么圆的周长也扩大a倍。 ( )
4、圆的直径越长,圆周率越大 ( )
×
二、判断
5厘米
求下面圆的周长。
4厘米
3厘米
3.14×3=9.42(厘米)
3.14×4=12.56(厘米)
3.14×5=15.7(厘米)
4分米
2米
求下面圆的周长。
圆的周长
青岛版六年级上册
围成圆的曲线的长叫做圆的周长
10cm
20cm
30cm
40cm
C=3d
周三径一
若想研究“周三径一”的说法是否正确,应该如何做?
研究“周三径一”是否正确
圆 直径(厘米) 若“周三径一 ”正确,周长为(厘米) 实际测量得到周长为(厘米) 研究结论
A
B
C
4
5
6
12
15
18
活动要求:
1.同桌两人一组,用合适的方法相互配合测量圆的周长。(测量结果保留一位小数)
2.在研究问题的时候,尽量不要有成见,客观真实地记录数据。
研究“周三径一”是否正确
圆 直径(厘米) 若“周三径一 ”正确,周长为(厘米) 实际测量得到周长为(厘米) 研究结论
A
B
C
4
5
6
12
15
18
C≈3d
3×10=30(厘米)
刘徽在《九章算术注》中提出了“割圆术”,并用割圆术将“3”改进成了“3.14”。刘徽在割圆中提出“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体,而无所失矣”。
刘徽
“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体,而无所失矣”
割圆术
刘徽
C≈3.14d
3.14×10=31.4(厘米)
祖冲之
隨书律历志
将“3.14”进一步改进为3.1415926到3.1415927之间。
祖冲之
C≈3.1415927d
3.1415927×10=
31.415927(厘米)
《周髀算经》
刘徽
祖冲之
后来……
C≈3d
C≈3.14d
C≈3.1415927d
C≈3.1415926……×d
圆的周长和它的直径的比值是一个固定的数,这个比值叫做圆周率,用希腊字母π(读作pài)表示。圆周率是一个无限不循环的小数,在实际应用中我们一般取它的近似值,即π≈3.14。
2016年瑞士物理学家用一台配置24个6 TB硬盘的电脑,花了105天,计算到圆周率小数点后的第22.4万亿位。2020年在3月14日,也就是国际圆周率这天,谷歌工程师利用谷歌云计算资源,花了121天,成功将圆周率π计算到小数点后31.4万亿位,刷新了世界纪录。假设一秒读一位的,一个人不分昼夜的读完这些天文般的数字,要花99万多年,若将它们全部写在厚0.1毫米的纸上,每张纸上写一万位,这些纸堆起来将比31座珠穆朗玛峰还高。
一、填空
1、《周髀算经》提出了___________的说法。
2、______在《九章算术注》采用________将 3 改进成了3.14.
3、_________计算是世界上第一个把圆周率的值精确到七位小数的人
4、世界圆周率日是___________
周三径一
刘徽
割圆术
祖冲之
3月14日
1、两个圆的周长相等,那么这两个圆的直径也相等。 ( )
√
×
√
3、 π=3.14 ( )
2、圆的直径扩大a倍,那么圆的周长也扩大a倍。 ( )
4、圆的直径越长,圆周率越大 ( )
×
二、判断
5厘米
求下面圆的周长。
4厘米
3厘米
3.14×3=9.42(厘米)
3.14×4=12.56(厘米)
3.14×5=15.7(厘米)
4分米
2米
求下面圆的周长。
