2021-2022学年北师大版七年级数学下册2.3平行线的性质解答题专题训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版七年级数学下册2.3平行线的性质解答题专题训练(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 326.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-20 17:24:17 | ||
图片预览



文档简介
2021-2022学年北师大版七年级数学下册《2-3平行线的性质》解答题专题训练(附答案)
1.如图,点G、F分别在AC、BC上,点D、E在AB上,CD∥EF,∠1=∠2,∠3=60°.请问:
(1)GD与CB有怎样的位置关系?为什么?
(2)求∠ACB的度数.
2.如图,BC与AF相交于点E,AB∥CD,∠1=∠2,∠3=∠4,求证:AD∥BE.
3.如图,已知CF⊥AB于点F,ED⊥AB于点D,∠1=∠2,求证:∠BCA+∠FGC=180°.
4.如图,∠1=∠2,∠3=∠4.
(1)试说明AB∥CD;
(2)若∠BAD=∠BDA,且∠EBF=110°,求∠ADC的度数.
5.如图,一条直线分别与直线BE、直线CE、直线BF、直线CF相交于A,G,H,D,且∠1=∠2,∠B=∠C.
求证:(1)BF∥EC;
(2)∠A=∠D.
6.(1)如图1,已知,a∥b,∠1=∠2,求证:m∥n;
(2)如图,已知,∠AEF+∠EFC=180°,∠AEG=∠HFD,求证:∠G=∠H.
7.如图,已知AC∥FE,∠1+∠2=180°.
(1)求证:∠FAB=∠BDC;
(2)若AC平分∠FAD,EF⊥BE于点E,∠FAD=80°,求∠BCD的度数.
8.探究:如图①,DE∥BC,EF∥AB,若∠ABC=50°,求∠DEF的度数.
请将下面的解答过程补充完整,并填空.
解:因为DE∥BC,
所以∠DEF= ( ).
因为EF∥AB,
所以 =∠ABC( ).
所以∠DEF=∠ABC(等量代换).
因为∠ABC=50°,
所以∠DEF= °.
应用:如图②,DE∥BC,EF∥AB,若∠ABC=65°,求∠DEF的度数.
9.已知一角的两边与另一个角的两边分别平行,试探索这两个角之间的关系,并说明你的结论.
(1)如图1所示,AB∥EF,BC∥DE,则∠1与∠2的关系是 ;
(2)如图2所示,AB∥EF,BC∥DE,则∠1与∠2的关系是 ;
(3)经过上述探索,我们可以得到一个结论(试用文字语言表述): ;
(4)若两个角的两边分别平行,且一个角比另一个角的2倍少30°,则这两个分别是多少度?
10.如图,AB∥CD,EM是∠AMF的平分线,NF是∠CNE的平分线,EN、MF交于点O.
(1)若∠AMF=52°,∠CNE=38°,求∠MEN、∠MFN的度数;
(2)若2∠MFN﹣∠MEN=45°,求出∠AMF的度数;
(3)探究∠MEN、∠MFN与∠MON之间存在怎样的数量关系.(直接写出结果)
11.如图①,AB∥CD,点E在直线AB与CD之间,连接AE、CE,则有∠AEC=∠A+∠DCE.
【感知】证明:如图①,过点E作EF∥AB,则有∠AEC=∠1+∠2=∠A+∠DCE.
【探究】当点E在如图②的位置时,其他条件不变,试说明∠A+∠AEC+∠C=360°.
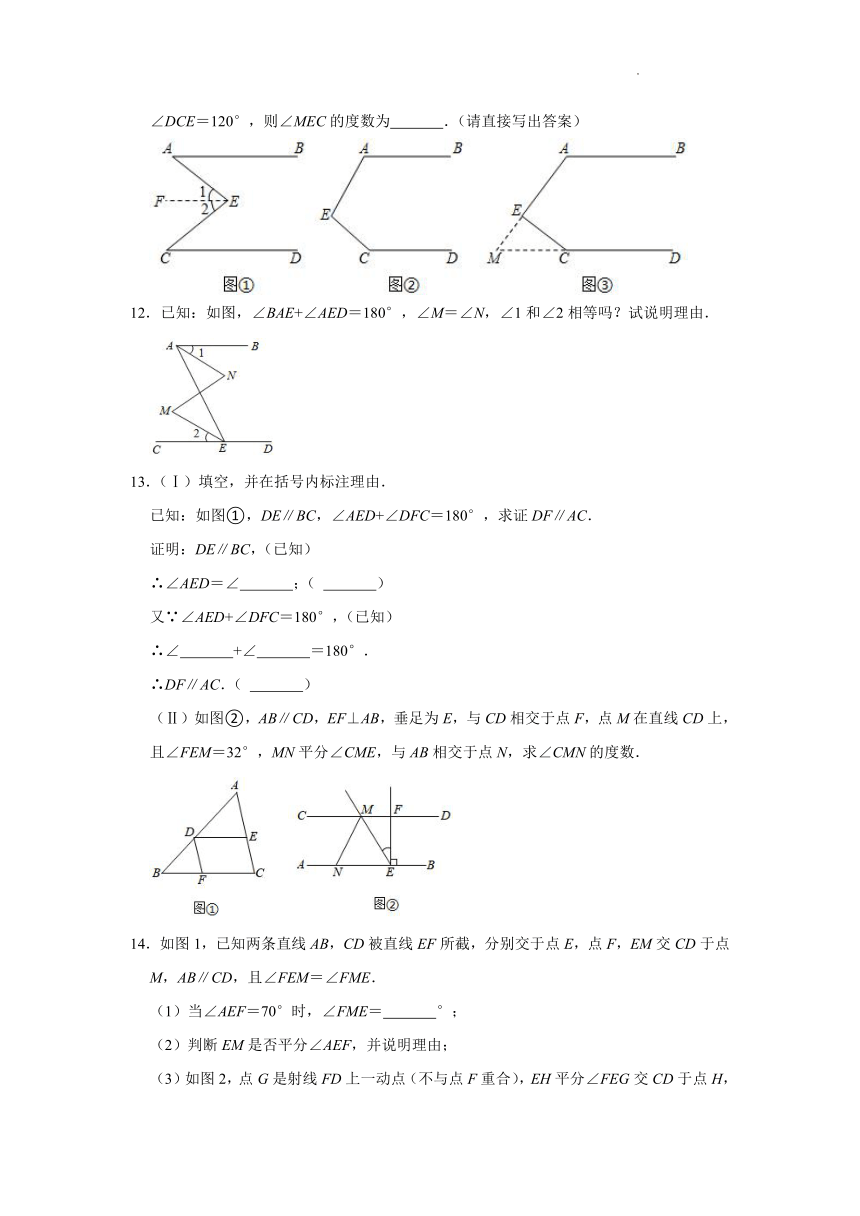
【应用】如图③,在图②的条件下,延长线段AE交直线CD于点M,已知∠A=130°,∠DCE=120°,则∠MEC的度数为 .(请直接写出答案)
12.已知:如图,∠BAE+∠AED=180°,∠M=∠N,∠1和∠2相等吗?试说明理由.
13.(Ⅰ)填空,并在括号内标注理由.
已知:如图①,DE∥BC,∠AED+∠DFC=180°,求证DF∥AC.
证明:DE∥BC,(已知)
∴∠AED=∠ ;( )
又∵∠AED+∠DFC=180°,(已知)
∴∠ +∠ =180°.
∴DF∥AC.( )
(Ⅱ)如图②,AB∥CD,EF⊥AB,垂足为E,与CD相交于点F,点M在直线CD上,且∠FEM=32°,MN平分∠CME,与AB相交于点N,求∠CMN的度数.
14.如图1,已知两条直线AB,CD被直线EF所截,分别交于点E,点F,EM交CD于点M,AB∥CD,且∠FEM=∠FME.
(1)当∠AEF=70°时,∠FME= °;
(2)判断EM是否平分∠AEF,并说明理由;
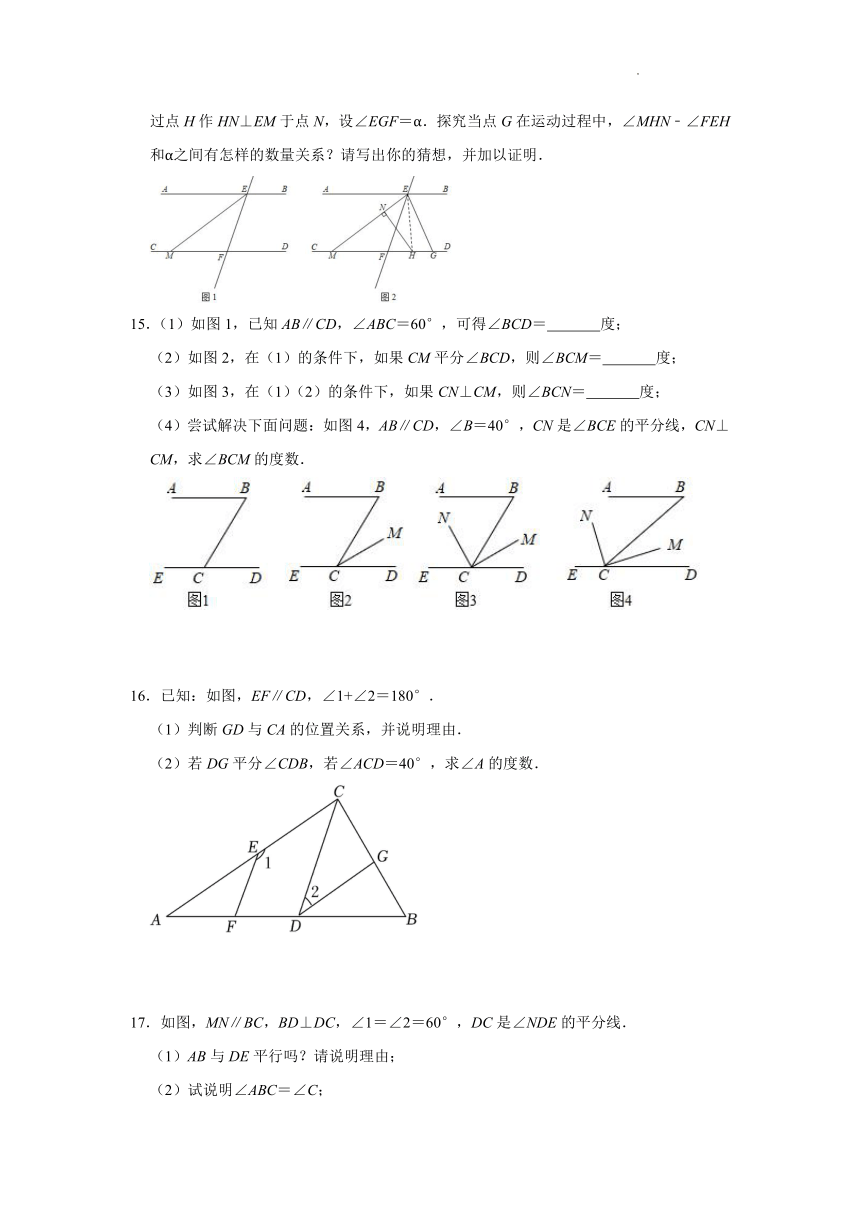
(3)如图2,点G是射线FD上一动点(不与点F重合),EH平分∠FEG交CD于点H,过点H作HN⊥EM于点N,设∠EGF=α.探究当点G在运动过程中,∠MHN﹣∠FEH和α之间有怎样的数量关系?请写出你的猜想,并加以证明.
15.(1)如图1,已知AB∥CD,∠ABC=60°,可得∠BCD= 度;
(2)如图2,在(1)的条件下,如果CM平分∠BCD,则∠BCM= 度;
(3)如图3,在(1)(2)的条件下,如果CN⊥CM,则∠BCN= 度;
(4)尝试解决下面问题:如图4,AB∥CD,∠B=40°,CN是∠BCE的平分线,CN⊥CM,求∠BCM的度数.
16.已知:如图,EF∥CD,∠1+∠2=180°.
(1)判断GD与CA的位置关系,并说明理由.
(2)若DG平分∠CDB,若∠ACD=40°,求∠A的度数.
17.如图,MN∥BC,BD⊥DC,∠1=∠2=60°,DC是∠NDE的平分线.
(1)AB与DE平行吗?请说明理由;
(2)试说明∠ABC=∠C;
(3)试说明BD是∠ABC的平分线.
18.已知,AB∥DE,点C在AB上方,连接BC、CD.
(1)如图1,求证:∠BCD+∠CDE=∠ABC;
(2)如图2,过点C作CF⊥BC交ED的延长线于点F,探究∠ABC和∠F之间的数量关系;
(3)如图3,在(2)的条件下,∠CFD的平分线交CD于点G,连接GB并延长至点H,若BH平分∠ABC,求∠BGD﹣∠CGF的值.
19.已知直线AB∥CD,P为平面内一点,连接PA、PD.
(1)如图1,已知∠A=50°,∠D=150°,求∠APD的度数;
(2)如图2,判断∠PAB、∠CDP、∠APD之间的数量关系为 .
(3)如图3,在(2)的条件下,AP⊥PD,DN平分∠PDC,若∠PAN+∠PAB=∠APD,求∠AND的度数.
20.【感知】已知:如图①,点E在AB上,且CE平分∠ACD,∠1=∠2.求证:AB∥CD.
将下列证明过程补充完整:
证明:∵CE平分∠ACD(已知),
∴∠2=∠ (角平分线的定义),
∵∠1=∠2(已知),
∴∠1=∠ (等量代换),
∴AB∥CD( ).
【探究】已知:如图②,点E在AB上,且CE平分∠ACD,AB∥CD.求证:∠1=∠
【应用】如图③,BE平分∠DBC,点A是BD上一点,过点A作AE∥BC交BE于点E,∠ABC:∠BAE=4:5,直接写出∠E的度数.
参考答案
1.解:(1)DG∥BC,
理由:∵CD∥EF,
∴∠2=∠DCF,
∵∠1=∠2,
∴∠1=∠DCF,
∴DG∥BC;
(2)由(1)知,DG∥BC,
∴∠ACB=∠3=60°.
2.证明:∵AB∥CD,
∴∠1=∠ACD,
∵∠1=∠2,
∴∠2=∠ACD,
∴∠2+∠CAE=∠ACD+∠CAE,
∴∠DAC=∠4,
∵∠3=∠4,
∴∠DAC=∠3,
∴AD∥BE.
3.证明:∵CF⊥AB,ED⊥AB,
∴CF∥ED,
∴∠1=∠BCF,
∵∠1=∠2,
∴∠BCF=∠2,
∴FG∥BC,
∴∠BCA+∠FGC=180°.
4.解:(1)∵∠1=∠2,
∴BM∥CN,
∴∠MBC=∠NCB,
∵∠3=∠4,
∴∠MBC+∠3=∠NCB+∠4,
即∠ABC=∠DCB,
∴AB∥CD;
(2)∵∠EBF=∠ABD,∠EBF=110°,
∴∠ABD=110°,
∵∠BAD+∠BDA+∠ABD=180°,∠BAD=∠BDA,
∴∠BAD=∠BDA=×(180°﹣110°)=35°,
∵AB∥CD,
∴∠ADC=∠BAD=35°.
5.证明:(1)∵∠1=∠2(已知),
∴BF∥EC(同位角相等,两直线平行);
(2)∵BF∥EC(已证),
∴∠C=∠BFD(两直线平行,同位角相等),
∵∠B=∠C(已知),
∴∠B=∠BFD(等量代换),
∴AB∥CD(内错角相等,两直线平行),
∴∠A=∠D(两直线平行,内错角相等).
6.证明:(1)如图:
∵a∥b,
∴∠3=∠2,
∵∠1=∠2,
∴∠1=∠3,
又∵∠1=∠4,
∴∠3=∠4,
∴m∥n.
(2)∵∠AEF+∠EFC=180°,
∴AB∥CD,
∴∠AEF=∠EFD,
又∵∠AEG=∠HFD,
∴∠AEF﹣∠AEG=∠EFD﹣∠HFD,即∠GEF=∠EFH,
∴GE∥FH,
∴∠G=∠H.
7.(1)证明:∵AC∥EF,
∴∠1+∠FAC=180°,
又∵∠1+∠2=180°,
∴∠FAC=∠2,
∴FA∥CD,
∴∠FAB=∠BDC;
(2)解:∵AC平分∠FAD,
∴∠FAC=∠CAD,∠FAD=2∠FAC,
由(1)知∠FAC=∠2,
∴∠FAD=2∠2,
∴∠2=∠FAD,
∵∠FAD=80°,
∴∠2=×80°=40°,
∵EF⊥BE,AC∥EF,
∴AC⊥BE,
∴∠ACB=90°,
∴∠BCD=90°﹣∠2=50°.
8.解:探究:如图①,
因为DE∥BC,
所以∠DEF=∠EFC(两直线平行,内错角相等),
因为EF∥AB,
所以∠EFC=∠ABC(两直线平行,同位角相等),
所以∠DEF=∠ABC(等量代换),
因为∠ABC=50°,
所以∠DEF=50°.
故答案为:∠EFC;两直线平行,内错角相等;∠EFC;两直线平行,同位角相等;50;
应用:如图②,
∵DE∥BC,∠ABC=65°,
∴∠D=∠ABC=65°,
∵EF∥AB,
∴∠D+∠DEF=180°,
∴∠DEF=180°﹣65°=115°.
9.解:(1)如图1.
∵AB∥EF,
∴∠1=∠3.
∵BC∥DE,
∴∠3=∠2.
∴∠1=∠2.
故答案为:∠1=∠2.
(2)∵AB∥EF,
∴∠1=∠BGE.
∵BC∥DE,
∴∠2+∠BGE=180°.
∴∠1+∠2=180°.
故答案为:∠1+∠2=180°.
(3)由(1)、(2)得:一角的两边与另一个角的两边分别平行,则这两个角要么相等,要么互补.
(4)设这两个角分别是∠1、∠2,且∠1=2∠2﹣30°.
∵∠1+∠2=180°,
∴2∠2﹣30°+∠2=180°.
∴∠2=70°.
∴∠1=2×70°﹣30°=110°.
∴这两个角分别为70°、110°,
或∠1=∠2,且∠1=2∠2﹣30°,
∴∠1=∠2=30°.
10.解:(1)作EH∥AB,如图,
∵AB∥CD,
∴EH∥CD,
∴∠1=∠AME,∠2=∠CNE,
∴∠MEN=∠AME+∠CNE,
∵EM是∠AMF的平分线,
∴∠AME=∠AMF,
∴∠MEN=∠AMF+∠CNE=×52°+38°=64°;
同理可得∠MFN=∠AMF+∠CNE=52°+×38°=71°;
(2)∵∠MEN=∠AMF+∠CNE,∠MFN=∠AMF+∠CNE,
∴2∠MFN=2∠AMF+∠CNE,
∴2∠MFN﹣∠MEN=∠AMF,
∵2∠MFN﹣∠MEN=45°,
∴∠AMF=45°,
∴∠AMF=30°;
(3)与(1)的证明方法一样可得∠MON=∠AMF+∠CNE,
而∠MEN=∠AMF+∠CNE,∠MFN=∠AMF+∠CNE,
∴2∠MEN=∠AMF+2∠CNE,2∠MFN=2∠AMF+∠CNE,
∴2∠MEN+2∠MFN=3(∠AMF+∠CNE),
∴∠AMF+∠CNE=(∠MEN+∠MFN),
∴∠MON=(∠MEN+∠MFN).
11.【感知】证明:如图①,
过点E作EF∥AB,
∴∠A=∠1,
∵AB∥CD,
∵EF∥AB,
∴CD∥EF,
∴∠2=∠DCE,
∵∠AEC=∠1+∠2,
∴∠AEC=∠A+∠DCE(等量代换),
【探究】证明:过点E作EF∥AB,如图②所示:
∵AB∥CD,
∴EF∥CD,
∴∠A+∠AEF=180°,∠C+∠CEF=180°,
∴∠A+∠AEC+∠C=∠A+∠AEF+∠C+∠CEF=180°+180°=360°;
【应用】解:同【探究】得:∠A+∠AEC+∠DCE=360°,
∴∠AEC=360°﹣∠A﹣∠DCE=360°﹣130°﹣120°=110°,
∴∠MEC=180°﹣∠AEC=180°﹣110°=70°,
故答案为:70°.
12.解:∠1和∠2相等.
证明:∵∠BAE+∠AED=180°(已知),
∴AB∥CD.
∴∠BAE=∠AEC (两直线平行,内错角相等).
又∵∠M=∠N (已知),
∴AN∥ME (内错角相等,两直线平行).
∴∠NAE=∠AEM (两直线平行,内错角相等).
∴∠BAE﹣∠NAE=∠AEC﹣∠AEM.
即∠1=∠2(等量代换).
故∠1和∠2相等.
13.(Ⅰ)证明:DE∥BC(已知),
∴∠AED=∠C(两直线平行,同位角相等),
又∵∠AED+∠DFC=180°(已知),
∴∠DFC+∠C=180°,
∴DF∥AC(同旁内角互补,两直线平行).
故答案为:C;两直线平行,同位角相等;DFC;C;同旁内角互补,两直线平行.
(Ⅱ)解:∵EF⊥AB,
∴∠AEF=90°,
∵∠FEM=32°,
∴∠AEM=90°﹣∠FEM=90°﹣32°=58°,
∵AB∥CD,
∴∠CME+∠AEM=180°,
∴∠CME=180°﹣58°=122°,
∵MN平分∠CME,
∴∠CMN=∠CME=×122°=61°.
14.解:(1)∵AB∥CD,
∴∠AEM=∠FME,
又∵∠FEM=∠FME,
∴∠AEM=∠FEM,
∵∠AEF=70°,
∴∠FME=∠AEM=∠AEF=35°;
故答案为:35;
(2)由(1)得∠AEM=∠FEM,
∴EM平分∠AEF;
(3)∠MHN﹣∠FEH=α.
证明:∵AB∥CD,
∴∠BEG=∠EGF=α,
∵EH平分∠FEG,
∴∠FEH=∠HEG=∠FEG,
∴∠FEH+α=∠BEG+∠GEH=∠BEH,
∵EM平分∠AEF,EH平分∠FEG,
∴∠MEH=∠AEG=(180°﹣α)=90°﹣,
在Rt△EHN中,∠EHN=90°﹣∠MEH=90°﹣(90°﹣α)=α,
∵AB∥CD,
∴∠BEH=∠EHF,即α+∠GEH=∠EHN+∠NHM,
∴α+∠FEH=α+∠NHM,
∴∠MHN﹣∠FEH=α.
15.解(1)∵AB∥CD,∠ABC=60°,
∴∠BCD=∠ABC=60°,
故答案为:60;
(2)∵AB∥CD,∠ABC=60°,
∴∠BCD=∠ABC=60°,
∵CM平分∠BCD,
∴∠BCM=∠DCM=∠BCD=30°;
故答案为:30;
(3)∵CN⊥CM,
∴∠NCM=90°,
∵∠BCM=30°,
∴∠BCN=∠NCM﹣∠BCM=90°﹣30°=60°;
故答案为:60;
(4)∵AB∥CD,
∴∠B+∠BCE=180°,
∵∠B=40°,
∴∠BCE=180°﹣∠B=180°﹣40°=140°,
又∵CN是∠BCE的平分线,
∴∠BCN=∠BCE=×140°=70°,
∵CN⊥CM,
∴∠BCN+∠BCM=90°,
∴∠BCM=90°﹣∠BCN=90°﹣70°=20°.
16.解:(1)GD∥CA.
理由:∵EF∥CD,
∴∠1+∠ACD=180°,
又∵∠1+∠2=180°,
∴∠ACD=∠2,
∴GD∥CA;
(2)∵GD∥CA,
∴∠2=∠ACD=40°,
∵DG平分∠CDB,
∴∠BDG=∠2=40°,
∵GD∥CA,
∴∠A=∠BDG=40°.
17.解:(1)AB∥DE,理由如下:
∵MN∥BC,( 已知 )
∴∠ABC=∠1=60°.( 两直线平行,内错角相等 )
又∵∠1=∠2,( 已知 )
∴∠ABC=∠2.( 等量代换 )
∴AB∥DE.( 同位角相等,两直线平行 );
(2)∵MN∥BC,
∴∠NDE+∠2=180°,
∴∠NDE=180°﹣∠2=180°﹣60°=120°.
∵DC是∠NDE的平分线,
∴∠EDC=∠NDC=∠NDE=60°.
∵MN∥BC,
∴∠C=∠NDC=60°.∴∠ABC=∠C.
(3)∠ADC=180°﹣∠NDC=180°﹣60°=120°,
∵BD⊥DC,
∴∠BDC=90°.
∴∠ADB=∠ADC﹣∠BDC=120°﹣90°=30°.
∵MN∥BC,
∴∠DBC=∠ADB=30°.
∴∠ABD=∠DBC=∠ABC.∴BD是∠ABC的平分线.
18.(1)证明:过点C作CM∥AB,如图1,
∴∠ABC=∠BCM,
∵AB∥ED,
∴∠CDE=∠DCM,
∵∠BCM=∠BCD+∠DCM,
∴∠ABC=∠BCD+∠CDE;
(2)解:∠ABC﹣∠F=90°,理由:
过点C作CN∥AB,如图2,
∴∠ABC=∠BCN,
∵AB∥ED,
∴CN∥EF,
∴∠F=∠FCN,
∵∠BCN﹣∠BCF+∠FCN,
∴∠ABC=∠BCF+∠F,
∵CF⊥BC,
∴∠BCF=90°,
∴∠ABC=90°+∠F,
即∠ABC﹣∠F=90°;
(3)延长HG交EF于点Q,过点G作GP∥EF,如图3,
∴∠BGD=∠CGQ,
∵AB∥DE,
∴∠ABH=∠EQG,
∵GP∥EF,
∴∠EQG=∠PGQ,∠EFG=∠PGF,
∴∠PGQ=∠ABH,
∴∠BGD﹣∠CGF=∠CGQ﹣∠CGF=∠FGQ,
∵∠FGQ=∠PGQ﹣∠PGF,
∴∠FGQ=∠ABH﹣∠EFG,
∵BH平分∠ABC,FG平分∠CFD,
∴∠ABH=∠ABC,∠EFG=∠CFD,
∴∠FGQ=∠ABC﹣∠CFD=(∠ABC﹣∠CFD),
由(2)可得:∠ABC﹣∠CFD=90°,
∴∠FGQ=×90°=45°,
即∠BGD﹣∠CGF=45°.
19.解:(1)如图1,过点P作EF∥AB,
∵∠A=50°,
∴∠APE=∠A=50°,
∵AB∥CD,
∴EF∥CD,
∴∠CDP+∠EPD=180°,
∵∠D=150°,
∴∠EPD=180°﹣150°=30°,
∴∠APD=∠APE+∠EPD=50°+30°=80°;
(2)如图2,过点P作EF∥AB,则AB∥EF∥CD,
∴∠CDP=∠DPF,∠FPA+∠PAB=180°,
∵∠FPA=∠DPF﹣APD,
∴∠DPF﹣APD+∠PAB=180°,
∴∠CDP+∠PAB﹣APD=180°,
故答案为:∠CDP+∠PAB﹣APD=180°;
(3)如图3,PD交AN于点O,
∵AP⊥PD,
∴∠APO=90°,
∵∠PAN+∠PAB=∠APD,
∴∠PAN+∠PAB=90°,
∵∠POA+∠PAN=90°,
∴∠POA=∠PAB,
∵∠POA=∠NOD,
∴∠NOD=∠PAB,
∵DN平分∠PDC,
∴∠ODN=∠PDC,
∴∠AND=180°﹣∠NOD﹣∠ODN
=180°﹣(∠PAB+∠PDC),
由(2)得:∠CDP+∠PAB﹣APD=180°,
∴∠CDP+∠PAB=180°+∠APD,
∴∠AND=180°﹣(∠PAB+∠PDC)
=180°﹣(180°+∠APD)
=180°﹣(180°+90°)
=45°.
20.【感知】解:∵CE平分∠ACD(已知),
∴∠2=∠DCE(角平分线的定义),
∵∠1=∠2(已知),
∴∠1=∠DCE(等量代换),
∴AB∥CD(内错角相等,两直线平行).
故答案为:DCE;DCE;内错角相等,两直线平行;
【探究】证明:∵CE平分∠ACD,
∴∠2=∠DCE,
∵AB∥CD,
∴∠1=∠DCE,
∴∠1=∠2;
【应用】∵BE平分∠DBC,
∴∠ABE=∠CBE,
∵AE∥BC,
∴∠ABC+∠BAE=180°,∠E=∠CBE,
∵∠ABC:∠BAE=4:5,
∴∠ABC=80°,
∴∠CBE=40°,
∴∠E=∠CBE=40°
1.如图,点G、F分别在AC、BC上,点D、E在AB上,CD∥EF,∠1=∠2,∠3=60°.请问:
(1)GD与CB有怎样的位置关系?为什么?
(2)求∠ACB的度数.
2.如图,BC与AF相交于点E,AB∥CD,∠1=∠2,∠3=∠4,求证:AD∥BE.
3.如图,已知CF⊥AB于点F,ED⊥AB于点D,∠1=∠2,求证:∠BCA+∠FGC=180°.
4.如图,∠1=∠2,∠3=∠4.
(1)试说明AB∥CD;
(2)若∠BAD=∠BDA,且∠EBF=110°,求∠ADC的度数.
5.如图,一条直线分别与直线BE、直线CE、直线BF、直线CF相交于A,G,H,D,且∠1=∠2,∠B=∠C.
求证:(1)BF∥EC;
(2)∠A=∠D.
6.(1)如图1,已知,a∥b,∠1=∠2,求证:m∥n;
(2)如图,已知,∠AEF+∠EFC=180°,∠AEG=∠HFD,求证:∠G=∠H.
7.如图,已知AC∥FE,∠1+∠2=180°.
(1)求证:∠FAB=∠BDC;
(2)若AC平分∠FAD,EF⊥BE于点E,∠FAD=80°,求∠BCD的度数.
8.探究:如图①,DE∥BC,EF∥AB,若∠ABC=50°,求∠DEF的度数.
请将下面的解答过程补充完整,并填空.
解:因为DE∥BC,
所以∠DEF= ( ).
因为EF∥AB,
所以 =∠ABC( ).
所以∠DEF=∠ABC(等量代换).
因为∠ABC=50°,
所以∠DEF= °.
应用:如图②,DE∥BC,EF∥AB,若∠ABC=65°,求∠DEF的度数.
9.已知一角的两边与另一个角的两边分别平行,试探索这两个角之间的关系,并说明你的结论.
(1)如图1所示,AB∥EF,BC∥DE,则∠1与∠2的关系是 ;
(2)如图2所示,AB∥EF,BC∥DE,则∠1与∠2的关系是 ;
(3)经过上述探索,我们可以得到一个结论(试用文字语言表述): ;
(4)若两个角的两边分别平行,且一个角比另一个角的2倍少30°,则这两个分别是多少度?
10.如图,AB∥CD,EM是∠AMF的平分线,NF是∠CNE的平分线,EN、MF交于点O.
(1)若∠AMF=52°,∠CNE=38°,求∠MEN、∠MFN的度数;
(2)若2∠MFN﹣∠MEN=45°,求出∠AMF的度数;
(3)探究∠MEN、∠MFN与∠MON之间存在怎样的数量关系.(直接写出结果)
11.如图①,AB∥CD,点E在直线AB与CD之间,连接AE、CE,则有∠AEC=∠A+∠DCE.
【感知】证明:如图①,过点E作EF∥AB,则有∠AEC=∠1+∠2=∠A+∠DCE.
【探究】当点E在如图②的位置时,其他条件不变,试说明∠A+∠AEC+∠C=360°.
【应用】如图③,在图②的条件下,延长线段AE交直线CD于点M,已知∠A=130°,∠DCE=120°,则∠MEC的度数为 .(请直接写出答案)
12.已知:如图,∠BAE+∠AED=180°,∠M=∠N,∠1和∠2相等吗?试说明理由.
13.(Ⅰ)填空,并在括号内标注理由.
已知:如图①,DE∥BC,∠AED+∠DFC=180°,求证DF∥AC.
证明:DE∥BC,(已知)
∴∠AED=∠ ;( )
又∵∠AED+∠DFC=180°,(已知)
∴∠ +∠ =180°.
∴DF∥AC.( )
(Ⅱ)如图②,AB∥CD,EF⊥AB,垂足为E,与CD相交于点F,点M在直线CD上,且∠FEM=32°,MN平分∠CME,与AB相交于点N,求∠CMN的度数.
14.如图1,已知两条直线AB,CD被直线EF所截,分别交于点E,点F,EM交CD于点M,AB∥CD,且∠FEM=∠FME.
(1)当∠AEF=70°时,∠FME= °;
(2)判断EM是否平分∠AEF,并说明理由;
(3)如图2,点G是射线FD上一动点(不与点F重合),EH平分∠FEG交CD于点H,过点H作HN⊥EM于点N,设∠EGF=α.探究当点G在运动过程中,∠MHN﹣∠FEH和α之间有怎样的数量关系?请写出你的猜想,并加以证明.
15.(1)如图1,已知AB∥CD,∠ABC=60°,可得∠BCD= 度;
(2)如图2,在(1)的条件下,如果CM平分∠BCD,则∠BCM= 度;
(3)如图3,在(1)(2)的条件下,如果CN⊥CM,则∠BCN= 度;
(4)尝试解决下面问题:如图4,AB∥CD,∠B=40°,CN是∠BCE的平分线,CN⊥CM,求∠BCM的度数.
16.已知:如图,EF∥CD,∠1+∠2=180°.
(1)判断GD与CA的位置关系,并说明理由.
(2)若DG平分∠CDB,若∠ACD=40°,求∠A的度数.
17.如图,MN∥BC,BD⊥DC,∠1=∠2=60°,DC是∠NDE的平分线.
(1)AB与DE平行吗?请说明理由;
(2)试说明∠ABC=∠C;
(3)试说明BD是∠ABC的平分线.
18.已知,AB∥DE,点C在AB上方,连接BC、CD.
(1)如图1,求证:∠BCD+∠CDE=∠ABC;
(2)如图2,过点C作CF⊥BC交ED的延长线于点F,探究∠ABC和∠F之间的数量关系;
(3)如图3,在(2)的条件下,∠CFD的平分线交CD于点G,连接GB并延长至点H,若BH平分∠ABC,求∠BGD﹣∠CGF的值.
19.已知直线AB∥CD,P为平面内一点,连接PA、PD.
(1)如图1,已知∠A=50°,∠D=150°,求∠APD的度数;
(2)如图2,判断∠PAB、∠CDP、∠APD之间的数量关系为 .
(3)如图3,在(2)的条件下,AP⊥PD,DN平分∠PDC,若∠PAN+∠PAB=∠APD,求∠AND的度数.
20.【感知】已知:如图①,点E在AB上,且CE平分∠ACD,∠1=∠2.求证:AB∥CD.
将下列证明过程补充完整:
证明:∵CE平分∠ACD(已知),
∴∠2=∠ (角平分线的定义),
∵∠1=∠2(已知),
∴∠1=∠ (等量代换),
∴AB∥CD( ).
【探究】已知:如图②,点E在AB上,且CE平分∠ACD,AB∥CD.求证:∠1=∠
【应用】如图③,BE平分∠DBC,点A是BD上一点,过点A作AE∥BC交BE于点E,∠ABC:∠BAE=4:5,直接写出∠E的度数.
参考答案
1.解:(1)DG∥BC,
理由:∵CD∥EF,
∴∠2=∠DCF,
∵∠1=∠2,
∴∠1=∠DCF,
∴DG∥BC;
(2)由(1)知,DG∥BC,
∴∠ACB=∠3=60°.
2.证明:∵AB∥CD,
∴∠1=∠ACD,
∵∠1=∠2,
∴∠2=∠ACD,
∴∠2+∠CAE=∠ACD+∠CAE,
∴∠DAC=∠4,
∵∠3=∠4,
∴∠DAC=∠3,
∴AD∥BE.
3.证明:∵CF⊥AB,ED⊥AB,
∴CF∥ED,
∴∠1=∠BCF,
∵∠1=∠2,
∴∠BCF=∠2,
∴FG∥BC,
∴∠BCA+∠FGC=180°.
4.解:(1)∵∠1=∠2,
∴BM∥CN,
∴∠MBC=∠NCB,
∵∠3=∠4,
∴∠MBC+∠3=∠NCB+∠4,
即∠ABC=∠DCB,
∴AB∥CD;
(2)∵∠EBF=∠ABD,∠EBF=110°,
∴∠ABD=110°,
∵∠BAD+∠BDA+∠ABD=180°,∠BAD=∠BDA,
∴∠BAD=∠BDA=×(180°﹣110°)=35°,
∵AB∥CD,
∴∠ADC=∠BAD=35°.
5.证明:(1)∵∠1=∠2(已知),
∴BF∥EC(同位角相等,两直线平行);
(2)∵BF∥EC(已证),
∴∠C=∠BFD(两直线平行,同位角相等),
∵∠B=∠C(已知),
∴∠B=∠BFD(等量代换),
∴AB∥CD(内错角相等,两直线平行),
∴∠A=∠D(两直线平行,内错角相等).
6.证明:(1)如图:
∵a∥b,
∴∠3=∠2,
∵∠1=∠2,
∴∠1=∠3,
又∵∠1=∠4,
∴∠3=∠4,
∴m∥n.
(2)∵∠AEF+∠EFC=180°,
∴AB∥CD,
∴∠AEF=∠EFD,
又∵∠AEG=∠HFD,
∴∠AEF﹣∠AEG=∠EFD﹣∠HFD,即∠GEF=∠EFH,
∴GE∥FH,
∴∠G=∠H.
7.(1)证明:∵AC∥EF,
∴∠1+∠FAC=180°,
又∵∠1+∠2=180°,
∴∠FAC=∠2,
∴FA∥CD,
∴∠FAB=∠BDC;
(2)解:∵AC平分∠FAD,
∴∠FAC=∠CAD,∠FAD=2∠FAC,
由(1)知∠FAC=∠2,
∴∠FAD=2∠2,
∴∠2=∠FAD,
∵∠FAD=80°,
∴∠2=×80°=40°,
∵EF⊥BE,AC∥EF,
∴AC⊥BE,
∴∠ACB=90°,
∴∠BCD=90°﹣∠2=50°.
8.解:探究:如图①,
因为DE∥BC,
所以∠DEF=∠EFC(两直线平行,内错角相等),
因为EF∥AB,
所以∠EFC=∠ABC(两直线平行,同位角相等),
所以∠DEF=∠ABC(等量代换),
因为∠ABC=50°,
所以∠DEF=50°.
故答案为:∠EFC;两直线平行,内错角相等;∠EFC;两直线平行,同位角相等;50;
应用:如图②,
∵DE∥BC,∠ABC=65°,
∴∠D=∠ABC=65°,
∵EF∥AB,
∴∠D+∠DEF=180°,
∴∠DEF=180°﹣65°=115°.
9.解:(1)如图1.
∵AB∥EF,
∴∠1=∠3.
∵BC∥DE,
∴∠3=∠2.
∴∠1=∠2.
故答案为:∠1=∠2.
(2)∵AB∥EF,
∴∠1=∠BGE.
∵BC∥DE,
∴∠2+∠BGE=180°.
∴∠1+∠2=180°.
故答案为:∠1+∠2=180°.
(3)由(1)、(2)得:一角的两边与另一个角的两边分别平行,则这两个角要么相等,要么互补.
(4)设这两个角分别是∠1、∠2,且∠1=2∠2﹣30°.
∵∠1+∠2=180°,
∴2∠2﹣30°+∠2=180°.
∴∠2=70°.
∴∠1=2×70°﹣30°=110°.
∴这两个角分别为70°、110°,
或∠1=∠2,且∠1=2∠2﹣30°,
∴∠1=∠2=30°.
10.解:(1)作EH∥AB,如图,
∵AB∥CD,
∴EH∥CD,
∴∠1=∠AME,∠2=∠CNE,
∴∠MEN=∠AME+∠CNE,
∵EM是∠AMF的平分线,
∴∠AME=∠AMF,
∴∠MEN=∠AMF+∠CNE=×52°+38°=64°;
同理可得∠MFN=∠AMF+∠CNE=52°+×38°=71°;
(2)∵∠MEN=∠AMF+∠CNE,∠MFN=∠AMF+∠CNE,
∴2∠MFN=2∠AMF+∠CNE,
∴2∠MFN﹣∠MEN=∠AMF,
∵2∠MFN﹣∠MEN=45°,
∴∠AMF=45°,
∴∠AMF=30°;
(3)与(1)的证明方法一样可得∠MON=∠AMF+∠CNE,
而∠MEN=∠AMF+∠CNE,∠MFN=∠AMF+∠CNE,
∴2∠MEN=∠AMF+2∠CNE,2∠MFN=2∠AMF+∠CNE,
∴2∠MEN+2∠MFN=3(∠AMF+∠CNE),
∴∠AMF+∠CNE=(∠MEN+∠MFN),
∴∠MON=(∠MEN+∠MFN).
11.【感知】证明:如图①,
过点E作EF∥AB,
∴∠A=∠1,
∵AB∥CD,
∵EF∥AB,
∴CD∥EF,
∴∠2=∠DCE,
∵∠AEC=∠1+∠2,
∴∠AEC=∠A+∠DCE(等量代换),
【探究】证明:过点E作EF∥AB,如图②所示:
∵AB∥CD,
∴EF∥CD,
∴∠A+∠AEF=180°,∠C+∠CEF=180°,
∴∠A+∠AEC+∠C=∠A+∠AEF+∠C+∠CEF=180°+180°=360°;
【应用】解:同【探究】得:∠A+∠AEC+∠DCE=360°,
∴∠AEC=360°﹣∠A﹣∠DCE=360°﹣130°﹣120°=110°,
∴∠MEC=180°﹣∠AEC=180°﹣110°=70°,
故答案为:70°.
12.解:∠1和∠2相等.
证明:∵∠BAE+∠AED=180°(已知),
∴AB∥CD.
∴∠BAE=∠AEC (两直线平行,内错角相等).
又∵∠M=∠N (已知),
∴AN∥ME (内错角相等,两直线平行).
∴∠NAE=∠AEM (两直线平行,内错角相等).
∴∠BAE﹣∠NAE=∠AEC﹣∠AEM.
即∠1=∠2(等量代换).
故∠1和∠2相等.
13.(Ⅰ)证明:DE∥BC(已知),
∴∠AED=∠C(两直线平行,同位角相等),
又∵∠AED+∠DFC=180°(已知),
∴∠DFC+∠C=180°,
∴DF∥AC(同旁内角互补,两直线平行).
故答案为:C;两直线平行,同位角相等;DFC;C;同旁内角互补,两直线平行.
(Ⅱ)解:∵EF⊥AB,
∴∠AEF=90°,
∵∠FEM=32°,
∴∠AEM=90°﹣∠FEM=90°﹣32°=58°,
∵AB∥CD,
∴∠CME+∠AEM=180°,
∴∠CME=180°﹣58°=122°,
∵MN平分∠CME,
∴∠CMN=∠CME=×122°=61°.
14.解:(1)∵AB∥CD,
∴∠AEM=∠FME,
又∵∠FEM=∠FME,
∴∠AEM=∠FEM,
∵∠AEF=70°,
∴∠FME=∠AEM=∠AEF=35°;
故答案为:35;
(2)由(1)得∠AEM=∠FEM,
∴EM平分∠AEF;
(3)∠MHN﹣∠FEH=α.
证明:∵AB∥CD,
∴∠BEG=∠EGF=α,
∵EH平分∠FEG,
∴∠FEH=∠HEG=∠FEG,
∴∠FEH+α=∠BEG+∠GEH=∠BEH,
∵EM平分∠AEF,EH平分∠FEG,
∴∠MEH=∠AEG=(180°﹣α)=90°﹣,
在Rt△EHN中,∠EHN=90°﹣∠MEH=90°﹣(90°﹣α)=α,
∵AB∥CD,
∴∠BEH=∠EHF,即α+∠GEH=∠EHN+∠NHM,
∴α+∠FEH=α+∠NHM,
∴∠MHN﹣∠FEH=α.
15.解(1)∵AB∥CD,∠ABC=60°,
∴∠BCD=∠ABC=60°,
故答案为:60;
(2)∵AB∥CD,∠ABC=60°,
∴∠BCD=∠ABC=60°,
∵CM平分∠BCD,
∴∠BCM=∠DCM=∠BCD=30°;
故答案为:30;
(3)∵CN⊥CM,
∴∠NCM=90°,
∵∠BCM=30°,
∴∠BCN=∠NCM﹣∠BCM=90°﹣30°=60°;
故答案为:60;
(4)∵AB∥CD,
∴∠B+∠BCE=180°,
∵∠B=40°,
∴∠BCE=180°﹣∠B=180°﹣40°=140°,
又∵CN是∠BCE的平分线,
∴∠BCN=∠BCE=×140°=70°,
∵CN⊥CM,
∴∠BCN+∠BCM=90°,
∴∠BCM=90°﹣∠BCN=90°﹣70°=20°.
16.解:(1)GD∥CA.
理由:∵EF∥CD,
∴∠1+∠ACD=180°,
又∵∠1+∠2=180°,
∴∠ACD=∠2,
∴GD∥CA;
(2)∵GD∥CA,
∴∠2=∠ACD=40°,
∵DG平分∠CDB,
∴∠BDG=∠2=40°,
∵GD∥CA,
∴∠A=∠BDG=40°.
17.解:(1)AB∥DE,理由如下:
∵MN∥BC,( 已知 )
∴∠ABC=∠1=60°.( 两直线平行,内错角相等 )
又∵∠1=∠2,( 已知 )
∴∠ABC=∠2.( 等量代换 )
∴AB∥DE.( 同位角相等,两直线平行 );
(2)∵MN∥BC,
∴∠NDE+∠2=180°,
∴∠NDE=180°﹣∠2=180°﹣60°=120°.
∵DC是∠NDE的平分线,
∴∠EDC=∠NDC=∠NDE=60°.
∵MN∥BC,
∴∠C=∠NDC=60°.∴∠ABC=∠C.
(3)∠ADC=180°﹣∠NDC=180°﹣60°=120°,
∵BD⊥DC,
∴∠BDC=90°.
∴∠ADB=∠ADC﹣∠BDC=120°﹣90°=30°.
∵MN∥BC,
∴∠DBC=∠ADB=30°.
∴∠ABD=∠DBC=∠ABC.∴BD是∠ABC的平分线.
18.(1)证明:过点C作CM∥AB,如图1,
∴∠ABC=∠BCM,
∵AB∥ED,
∴∠CDE=∠DCM,
∵∠BCM=∠BCD+∠DCM,
∴∠ABC=∠BCD+∠CDE;
(2)解:∠ABC﹣∠F=90°,理由:
过点C作CN∥AB,如图2,
∴∠ABC=∠BCN,
∵AB∥ED,
∴CN∥EF,
∴∠F=∠FCN,
∵∠BCN﹣∠BCF+∠FCN,
∴∠ABC=∠BCF+∠F,
∵CF⊥BC,
∴∠BCF=90°,
∴∠ABC=90°+∠F,
即∠ABC﹣∠F=90°;
(3)延长HG交EF于点Q,过点G作GP∥EF,如图3,
∴∠BGD=∠CGQ,
∵AB∥DE,
∴∠ABH=∠EQG,
∵GP∥EF,
∴∠EQG=∠PGQ,∠EFG=∠PGF,
∴∠PGQ=∠ABH,
∴∠BGD﹣∠CGF=∠CGQ﹣∠CGF=∠FGQ,
∵∠FGQ=∠PGQ﹣∠PGF,
∴∠FGQ=∠ABH﹣∠EFG,
∵BH平分∠ABC,FG平分∠CFD,
∴∠ABH=∠ABC,∠EFG=∠CFD,
∴∠FGQ=∠ABC﹣∠CFD=(∠ABC﹣∠CFD),
由(2)可得:∠ABC﹣∠CFD=90°,
∴∠FGQ=×90°=45°,
即∠BGD﹣∠CGF=45°.
19.解:(1)如图1,过点P作EF∥AB,
∵∠A=50°,
∴∠APE=∠A=50°,
∵AB∥CD,
∴EF∥CD,
∴∠CDP+∠EPD=180°,
∵∠D=150°,
∴∠EPD=180°﹣150°=30°,
∴∠APD=∠APE+∠EPD=50°+30°=80°;
(2)如图2,过点P作EF∥AB,则AB∥EF∥CD,
∴∠CDP=∠DPF,∠FPA+∠PAB=180°,
∵∠FPA=∠DPF﹣APD,
∴∠DPF﹣APD+∠PAB=180°,
∴∠CDP+∠PAB﹣APD=180°,
故答案为:∠CDP+∠PAB﹣APD=180°;
(3)如图3,PD交AN于点O,
∵AP⊥PD,
∴∠APO=90°,
∵∠PAN+∠PAB=∠APD,
∴∠PAN+∠PAB=90°,
∵∠POA+∠PAN=90°,
∴∠POA=∠PAB,
∵∠POA=∠NOD,
∴∠NOD=∠PAB,
∵DN平分∠PDC,
∴∠ODN=∠PDC,
∴∠AND=180°﹣∠NOD﹣∠ODN
=180°﹣(∠PAB+∠PDC),
由(2)得:∠CDP+∠PAB﹣APD=180°,
∴∠CDP+∠PAB=180°+∠APD,
∴∠AND=180°﹣(∠PAB+∠PDC)
=180°﹣(180°+∠APD)
=180°﹣(180°+90°)
=45°.
20.【感知】解:∵CE平分∠ACD(已知),
∴∠2=∠DCE(角平分线的定义),
∵∠1=∠2(已知),
∴∠1=∠DCE(等量代换),
∴AB∥CD(内错角相等,两直线平行).
故答案为:DCE;DCE;内错角相等,两直线平行;
【探究】证明:∵CE平分∠ACD,
∴∠2=∠DCE,
∵AB∥CD,
∴∠1=∠DCE,
∴∠1=∠2;
【应用】∵BE平分∠DBC,
∴∠ABE=∠CBE,
∵AE∥BC,
∴∠ABC+∠BAE=180°,∠E=∠CBE,
∵∠ABC:∠BAE=4:5,
∴∠ABC=80°,
∴∠CBE=40°,
∴∠E=∠CBE=40°
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
