苏科版八年级数学下册 第9章中心对称图形—平行四边形 达标检测卷(word版含答案)
文档属性
| 名称 | 苏科版八年级数学下册 第9章中心对称图形—平行四边形 达标检测卷(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 365.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-20 00:00:00 | ||
图片预览



文档简介
第9章达标检测卷
一、选择题(每题3分,共24分)
1.下列图形中,是中心对称图形,但不是轴对称图形的是( )
A B C D
2.对角线互相垂直平分的四边形是( )
A.平行四边形、菱形 B.矩形、菱形
C.矩形、正方形 D.菱形、正方形
3.用两块边长为a的等边三角形纸片拼成的四边形是( )
A.等腰梯形 B.菱形 C.矩形 D.正方形
4.下列图形:①等腰三角形;②平行四边形;③矩形;④菱形;⑤正方形.用两个全等但不是等腰的直角三角形,一定能拼成的是( )
A.①②③ B.②③④
C.①③⑤ D.①②③④⑤
5.如图,已知矩形纸片ABCD,点E是AB的中点,点G是BC上的一点,∠BEG>60°,现沿直线EG将纸片折叠,使点B落在纸片上的点H处,连接AH,则与∠BEG相等的角有( )
A.4个
B.3个
C.2个
D.1个
6.如图,在边长为2的正方形ABCD中,M为边AD的中点,延长MD至点E,使ME=MC.以DE为边作正方形DEFG,点G在边CD上,则DG的长为( )
A.-1
B.3-
C.+1
D.-1
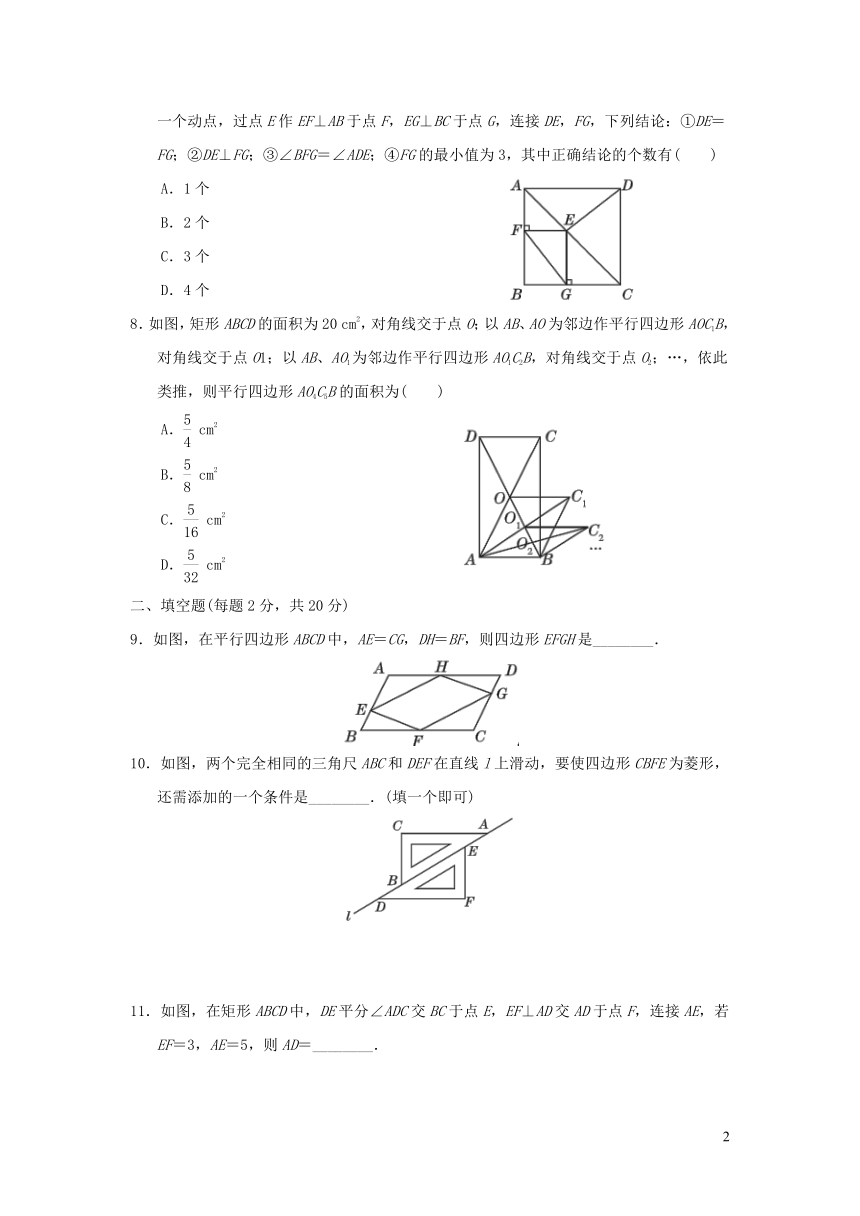
7.如图,在正方形ABCD中,AB=4,E为对角线AC上与A,C不重合的一个动点,过点E作EF⊥AB于点F,EG⊥BC于点G,连接DE,FG,下列结论:①DE=FG;②DE⊥FG;③∠BFG=∠ADE;④FG的最小值为3,其中正确结论的个数有( )
A.1个
B.2个
C.3个
D.4个
8.如图,矩形ABCD的面积为20 cm2,对角线交于点O;以AB、AO为邻边作平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边作平行四边形AO1C2B,对角线交于点O2;…,依此类推,则平行四边形AO4C5B的面积为( )
A. cm2
B. cm2
C. cm2
D. cm2
二、填空题(每题2分,共20分)
9.如图,在平行四边形ABCD中,AE=CG,DH=BF,则四边形EFGH是________.
10.如图,两个完全相同的三角尺ABC和DEF在直线l上滑动,要使四边形CBFE为菱形,还需添加的一个条件是________.(填一个即可)
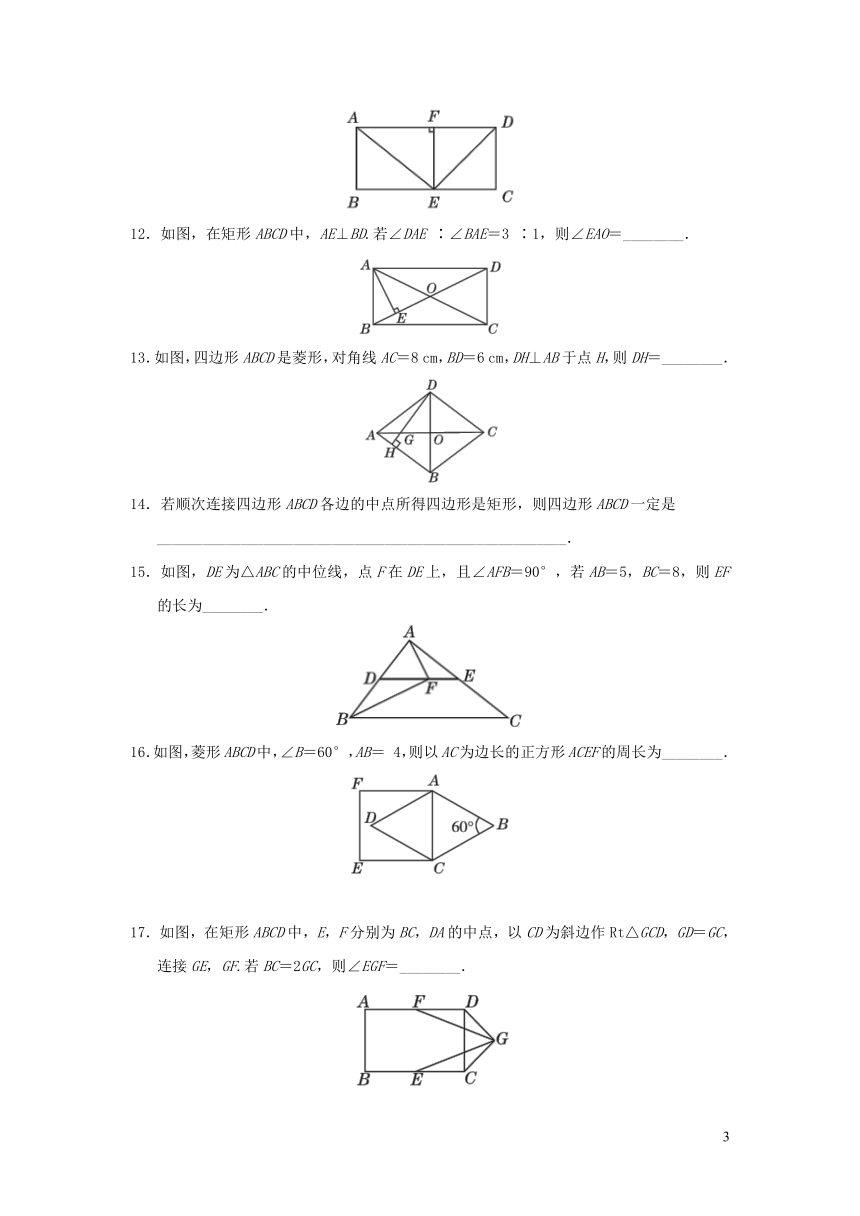
11.如图,在矩形ABCD中,DE平分∠ADC交BC于点E,EF⊥AD交AD于点F,连接AE,若EF=3,AE=5,则AD=________.
12.如图,在矩形ABCD中,AE⊥BD.若∠DAE ∶∠BAE=3 ∶1,则∠EAO=________.
13.如图,四边形ABCD是菱形,对角线AC=8 cm,BD=6 cm,DH⊥AB于点H,则DH=________.
14.若顺次连接四边形ABCD各边的中点所得四边形是矩形,则四边形ABCD一定是______________________________________________________.
15.如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为________.
16.如图,菱形ABCD中,∠B=60°,AB= 4,则以AC为边长的正方形ACEF的周长为________.
17.如图,在矩形ABCD中,E,F分别为BC,DA的中点,以CD为斜边作Rt△GCD,GD=GC,连接GE,GF.若BC=2GC,则∠EGF=________.
18.如图,E是正方形ABCD内一点,连接AE、BE、CE,将△ABE绕点B顺时针旋转90°到△CBE′的位置.若AE=1,BE=2,CE=3,则∠BE′C=________.
三、解答题(19~21题每题6分,22~23题每题7分,24~26题每题8分,共56分)
19.如图,在 ABCD中,直线EF∥BD,并且与CD、CB的延长线分别交于点E、F,交AD于点M,交AB于点N.求证:EN=FM.
20.已知:如图,△ABC中,∠C=90°,CD平分∠ACB,DE⊥BC于E,DF⊥AC于F.求证:四边形CFDE是正方形.
21.如图,在四边形ABCD中,AD∥BC,AD≠BC,∠B=90°,AG∥CD交BC于点G,点E、F分别为AG、CD的中点,连接DE、FG.
(1)求证:四边形DEGF是平行四边形;
(2)当点G是BC的中点时,求证:四边形DEGF是菱形.
22.如图,已知在菱形ABCD中,∠B=72°,请设计三种不同的方法,将菱形ABCD分割成四个三角形,使每个三角形都是等腰三角形.(要求画出分割线段,标出所得的三角形内角的度数.注:只要有一条分割线段位置不同,就认为是两种不同的方法)
23.如图,在 ABCD中,对角线AC与BD相交于点O,过点O的直线EF与BA、DC的延长线分别交于点E、F.
(1)求证:AE=CF;
(2)请再添加一个条件,使四边形BFDE是菱形,并说明理由.
24.已知四边形ABCD为矩形,E是AB延长线上的一点.
(1)若AC=EC,如图1,求证:四边形BECD为平行四边形;
(2)若AB=AD,点F是AB上的点,AF=BE,EG⊥AC于点G,如图2,求证:△DGF是等腰直角三角形.
25.如图,在 ABCD中,AB⊥AC,AB=1,BC=,对角线BD、AC交于点O.将直线AC绕点O顺时针旋转(不超过180°)分别交BC、AD于点E、F.
(1)试说明在旋转过程中,AF与CE总保持相等;
(2)证明:当旋转角为90°时,四边形ABEF是平行四边形;
(3)在旋转过程中,四边形BEDF可能是菱形吗?如果不可能,请说明理由;如果可能,求出此时AC绕点O顺时针旋转的角度.
26.已知,矩形ABCD中,AB=4 cm,BC=8 cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
(1)如图1,连接AF、CE.①求证四边形AFCE为菱形;②求AF的长.
(2)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周后停止.即点P沿A→F→B→A运动,点Q沿C→D→E→C运动.在运动过程中,
①已知点P的速度为每秒5 cm,点Q的速度为每秒4 cm,运动时间为
t s,当以A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.
②若点P、Q的运动路程分别为a cm、 b cm(ab≠0),已知以A、C、P、Q四点为顶点的四边形是平行四边形,直接写出a与b满足的数量关
系式.
答案
一、1.B 2.D 3.B 4.A 5.B
6.D 7.C 8.B
二、9.平行四边形
10.BE⊥CF(答案不唯一)
11.7 12.45° 13.4.8 cm
14.对角线互相垂直的四边形
15.1.5 16.16 17.45° 18.135°
三、19.证明:∵在 ABCD中,
AB∥CD,AD∥BC,EF∥BD,
∴四边形BNED和四边形FBDM为平行四边形,
∴FM=BD,EN=BD,∴EN=FM.
20.证明:∵DE⊥BC,DF⊥AC,
∴∠CFD=∠CED=90°,
又∵∠ACB=90°,
∴四边形CFDE是矩形.
又∵CD平分∠ACB,DE⊥BC,DF⊥AC,
∴DF=DE,
∴矩形CFDE是正方形.
21.证明:(1)∵AD∥BC,AG∥CD,
∴四边形AGCD为平行四边形,
∴AG=CD.
又∵点E、F分别为AG、CD的中点,
∴EG=AG=DC=DF,
∴四边形DEGF是平行四边形.
(2)连接DG.
∵G是BC的中点,
∴BG=CG,
由(1)易得AD=CG,∴AD=BG.
又∵AD∥BC,
∴四边形ABGD是平行四边形,
∴AB∥DG,
∴∠DGC=∠B=90°,
∴GF=CD=DF,
∴平行四边形DEGF是菱形.
22.解:方法多样,提供几例仅供参考,如图.
23.(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,BE∥DF,∴∠AEO=∠CFO.
在△AOE和△COF中,
∴△AOE≌△COF(AAS),∴AE=CF.
(2)解:当EF⊥BD时,四边形BFDE是菱形,理由如下:
∵四边形ABCD是平行四边形,
∴OB=OD.
∵△AOE≌△COF,
∴OE=OF,
∴四边形BFDE是平行四边形,
∵EF⊥BD,
∴四边形BFDE是菱形.
24.证明:(1)∵四边形ABCD为矩形,
∴AB∥CD,AB=CD,CB⊥AB.
又∵AC=EC,
∴AB=BE,
∴BE=CD,
∴四边形BECD为平行四边形.
(2)∵AB=AD,
∴矩形ABCD是正方形,
∵EG⊥AC,
∴∠E=90°-45°=45°=∠GAD,
∴GE=GA.
∵AF=BE,
∴AB=FE,
∴FE=AD.
在△EGF和△AGD中,
∴△EGF≌△AGD(SAS),
∴GF=GD,∠DGA=∠FGE,
∴∠DGF=∠DGA+∠AGF=∠FGE+∠AGF=∠AGE=90°,
∴△DGF是等腰直角三角形.
25.(1)解:在 ABCD中,AD∥BC,OA=OC,
∴∠1=∠2.
在△AOF和△COE中,
∠1=∠2,OA=OC,∠3=∠4,
∴△AOF≌△COE(ASA),
∴AF=CE.
(2)证明:此时∠AOF=90°.
∵AB⊥AC,
∴∠BAO=90°,
∴∠BAO=∠AOF=90°,
∴BA∥EF.
∵四边形ABCD是平行四边形,
∴AD∥BC,即AF∥BE.
∴四边形ABEF是平行四边形.
(3)解:可能.
∵AF=CE,AD∥BC,AD=BC,
∴FD∥BE,DF=BE,
∴四边形BEDF是平行四边形.
∴当EF⊥BD时, BEDF是菱形.
∵∠BAC=90°,∴BC2=AB2+AC2.
∵AB=1,BC=,
∴AC==2.
∵四边形ABCD是平行四边形.
∴OA=AC=×2=1.
∵在△AOB中,AB=AO=1,
∠BAO=90°,
∴∠BOA=45°.
∵EF⊥BD, ∴∠BOF=90°.
∴∠3=∠BOF-∠BOA=90°-45°=45°,
即旋转角为45°.
26.(1)①证明:∵在矩形ABCD中,AD∥BC,∴∠EAO=∠FCO,
∵EF垂直平分AC.
∴AO=CO,又∵∠AOE=∠COF,
∴△AOE≌△COF(ASA),
∴AE=CF,又∵AE∥CF,
∴四边形AFCE为平行四边形.
又∵EF⊥AC,
∴平行四边形AFCE为菱形.
②解:由①知AF=CF.
设AF=xcm,则CF=xcm,BF=BC-CF=(8-x)cm,在Rt△ABF中,
AB2+BF2=AF2,∴42+(8-x)2=x2,
解得x=5.
∴AF=5cm.
(2)①解:情况一:当P在AF上,Q在CD上时,四边形APCQ显然不可能是平行四边形.
情况二:当P在BF上,Q在ED上时,则当BP=DQ时,四边形APCQ为平行四边形,即8-5t=4t-4, t=.
情况三:当P在AB上,Q在ED上时,四边形APCQ显然不可能为平行四边形;
情况四:当P在AB上,Q在EC上时,四边形APCQ显然不可能为平行四边形.
∴当t=时,四边形APCQ为平行四边形.
②解:a+b=12.
1
一、选择题(每题3分,共24分)
1.下列图形中,是中心对称图形,但不是轴对称图形的是( )
A B C D
2.对角线互相垂直平分的四边形是( )
A.平行四边形、菱形 B.矩形、菱形
C.矩形、正方形 D.菱形、正方形
3.用两块边长为a的等边三角形纸片拼成的四边形是( )
A.等腰梯形 B.菱形 C.矩形 D.正方形
4.下列图形:①等腰三角形;②平行四边形;③矩形;④菱形;⑤正方形.用两个全等但不是等腰的直角三角形,一定能拼成的是( )
A.①②③ B.②③④
C.①③⑤ D.①②③④⑤
5.如图,已知矩形纸片ABCD,点E是AB的中点,点G是BC上的一点,∠BEG>60°,现沿直线EG将纸片折叠,使点B落在纸片上的点H处,连接AH,则与∠BEG相等的角有( )
A.4个
B.3个
C.2个
D.1个
6.如图,在边长为2的正方形ABCD中,M为边AD的中点,延长MD至点E,使ME=MC.以DE为边作正方形DEFG,点G在边CD上,则DG的长为( )
A.-1
B.3-
C.+1
D.-1
7.如图,在正方形ABCD中,AB=4,E为对角线AC上与A,C不重合的一个动点,过点E作EF⊥AB于点F,EG⊥BC于点G,连接DE,FG,下列结论:①DE=FG;②DE⊥FG;③∠BFG=∠ADE;④FG的最小值为3,其中正确结论的个数有( )
A.1个
B.2个
C.3个
D.4个
8.如图,矩形ABCD的面积为20 cm2,对角线交于点O;以AB、AO为邻边作平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边作平行四边形AO1C2B,对角线交于点O2;…,依此类推,则平行四边形AO4C5B的面积为( )
A. cm2
B. cm2
C. cm2
D. cm2
二、填空题(每题2分,共20分)
9.如图,在平行四边形ABCD中,AE=CG,DH=BF,则四边形EFGH是________.
10.如图,两个完全相同的三角尺ABC和DEF在直线l上滑动,要使四边形CBFE为菱形,还需添加的一个条件是________.(填一个即可)
11.如图,在矩形ABCD中,DE平分∠ADC交BC于点E,EF⊥AD交AD于点F,连接AE,若EF=3,AE=5,则AD=________.
12.如图,在矩形ABCD中,AE⊥BD.若∠DAE ∶∠BAE=3 ∶1,则∠EAO=________.
13.如图,四边形ABCD是菱形,对角线AC=8 cm,BD=6 cm,DH⊥AB于点H,则DH=________.
14.若顺次连接四边形ABCD各边的中点所得四边形是矩形,则四边形ABCD一定是______________________________________________________.
15.如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为________.
16.如图,菱形ABCD中,∠B=60°,AB= 4,则以AC为边长的正方形ACEF的周长为________.
17.如图,在矩形ABCD中,E,F分别为BC,DA的中点,以CD为斜边作Rt△GCD,GD=GC,连接GE,GF.若BC=2GC,则∠EGF=________.
18.如图,E是正方形ABCD内一点,连接AE、BE、CE,将△ABE绕点B顺时针旋转90°到△CBE′的位置.若AE=1,BE=2,CE=3,则∠BE′C=________.
三、解答题(19~21题每题6分,22~23题每题7分,24~26题每题8分,共56分)
19.如图,在 ABCD中,直线EF∥BD,并且与CD、CB的延长线分别交于点E、F,交AD于点M,交AB于点N.求证:EN=FM.
20.已知:如图,△ABC中,∠C=90°,CD平分∠ACB,DE⊥BC于E,DF⊥AC于F.求证:四边形CFDE是正方形.
21.如图,在四边形ABCD中,AD∥BC,AD≠BC,∠B=90°,AG∥CD交BC于点G,点E、F分别为AG、CD的中点,连接DE、FG.
(1)求证:四边形DEGF是平行四边形;
(2)当点G是BC的中点时,求证:四边形DEGF是菱形.
22.如图,已知在菱形ABCD中,∠B=72°,请设计三种不同的方法,将菱形ABCD分割成四个三角形,使每个三角形都是等腰三角形.(要求画出分割线段,标出所得的三角形内角的度数.注:只要有一条分割线段位置不同,就认为是两种不同的方法)
23.如图,在 ABCD中,对角线AC与BD相交于点O,过点O的直线EF与BA、DC的延长线分别交于点E、F.
(1)求证:AE=CF;
(2)请再添加一个条件,使四边形BFDE是菱形,并说明理由.
24.已知四边形ABCD为矩形,E是AB延长线上的一点.
(1)若AC=EC,如图1,求证:四边形BECD为平行四边形;
(2)若AB=AD,点F是AB上的点,AF=BE,EG⊥AC于点G,如图2,求证:△DGF是等腰直角三角形.
25.如图,在 ABCD中,AB⊥AC,AB=1,BC=,对角线BD、AC交于点O.将直线AC绕点O顺时针旋转(不超过180°)分别交BC、AD于点E、F.
(1)试说明在旋转过程中,AF与CE总保持相等;
(2)证明:当旋转角为90°时,四边形ABEF是平行四边形;
(3)在旋转过程中,四边形BEDF可能是菱形吗?如果不可能,请说明理由;如果可能,求出此时AC绕点O顺时针旋转的角度.
26.已知,矩形ABCD中,AB=4 cm,BC=8 cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
(1)如图1,连接AF、CE.①求证四边形AFCE为菱形;②求AF的长.
(2)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周后停止.即点P沿A→F→B→A运动,点Q沿C→D→E→C运动.在运动过程中,
①已知点P的速度为每秒5 cm,点Q的速度为每秒4 cm,运动时间为
t s,当以A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.
②若点P、Q的运动路程分别为a cm、 b cm(ab≠0),已知以A、C、P、Q四点为顶点的四边形是平行四边形,直接写出a与b满足的数量关
系式.
答案
一、1.B 2.D 3.B 4.A 5.B
6.D 7.C 8.B
二、9.平行四边形
10.BE⊥CF(答案不唯一)
11.7 12.45° 13.4.8 cm
14.对角线互相垂直的四边形
15.1.5 16.16 17.45° 18.135°
三、19.证明:∵在 ABCD中,
AB∥CD,AD∥BC,EF∥BD,
∴四边形BNED和四边形FBDM为平行四边形,
∴FM=BD,EN=BD,∴EN=FM.
20.证明:∵DE⊥BC,DF⊥AC,
∴∠CFD=∠CED=90°,
又∵∠ACB=90°,
∴四边形CFDE是矩形.
又∵CD平分∠ACB,DE⊥BC,DF⊥AC,
∴DF=DE,
∴矩形CFDE是正方形.
21.证明:(1)∵AD∥BC,AG∥CD,
∴四边形AGCD为平行四边形,
∴AG=CD.
又∵点E、F分别为AG、CD的中点,
∴EG=AG=DC=DF,
∴四边形DEGF是平行四边形.
(2)连接DG.
∵G是BC的中点,
∴BG=CG,
由(1)易得AD=CG,∴AD=BG.
又∵AD∥BC,
∴四边形ABGD是平行四边形,
∴AB∥DG,
∴∠DGC=∠B=90°,
∴GF=CD=DF,
∴平行四边形DEGF是菱形.
22.解:方法多样,提供几例仅供参考,如图.
23.(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,BE∥DF,∴∠AEO=∠CFO.
在△AOE和△COF中,
∴△AOE≌△COF(AAS),∴AE=CF.
(2)解:当EF⊥BD时,四边形BFDE是菱形,理由如下:
∵四边形ABCD是平行四边形,
∴OB=OD.
∵△AOE≌△COF,
∴OE=OF,
∴四边形BFDE是平行四边形,
∵EF⊥BD,
∴四边形BFDE是菱形.
24.证明:(1)∵四边形ABCD为矩形,
∴AB∥CD,AB=CD,CB⊥AB.
又∵AC=EC,
∴AB=BE,
∴BE=CD,
∴四边形BECD为平行四边形.
(2)∵AB=AD,
∴矩形ABCD是正方形,
∵EG⊥AC,
∴∠E=90°-45°=45°=∠GAD,
∴GE=GA.
∵AF=BE,
∴AB=FE,
∴FE=AD.
在△EGF和△AGD中,
∴△EGF≌△AGD(SAS),
∴GF=GD,∠DGA=∠FGE,
∴∠DGF=∠DGA+∠AGF=∠FGE+∠AGF=∠AGE=90°,
∴△DGF是等腰直角三角形.
25.(1)解:在 ABCD中,AD∥BC,OA=OC,
∴∠1=∠2.
在△AOF和△COE中,
∠1=∠2,OA=OC,∠3=∠4,
∴△AOF≌△COE(ASA),
∴AF=CE.
(2)证明:此时∠AOF=90°.
∵AB⊥AC,
∴∠BAO=90°,
∴∠BAO=∠AOF=90°,
∴BA∥EF.
∵四边形ABCD是平行四边形,
∴AD∥BC,即AF∥BE.
∴四边形ABEF是平行四边形.
(3)解:可能.
∵AF=CE,AD∥BC,AD=BC,
∴FD∥BE,DF=BE,
∴四边形BEDF是平行四边形.
∴当EF⊥BD时, BEDF是菱形.
∵∠BAC=90°,∴BC2=AB2+AC2.
∵AB=1,BC=,
∴AC==2.
∵四边形ABCD是平行四边形.
∴OA=AC=×2=1.
∵在△AOB中,AB=AO=1,
∠BAO=90°,
∴∠BOA=45°.
∵EF⊥BD, ∴∠BOF=90°.
∴∠3=∠BOF-∠BOA=90°-45°=45°,
即旋转角为45°.
26.(1)①证明:∵在矩形ABCD中,AD∥BC,∴∠EAO=∠FCO,
∵EF垂直平分AC.
∴AO=CO,又∵∠AOE=∠COF,
∴△AOE≌△COF(ASA),
∴AE=CF,又∵AE∥CF,
∴四边形AFCE为平行四边形.
又∵EF⊥AC,
∴平行四边形AFCE为菱形.
②解:由①知AF=CF.
设AF=xcm,则CF=xcm,BF=BC-CF=(8-x)cm,在Rt△ABF中,
AB2+BF2=AF2,∴42+(8-x)2=x2,
解得x=5.
∴AF=5cm.
(2)①解:情况一:当P在AF上,Q在CD上时,四边形APCQ显然不可能是平行四边形.
情况二:当P在BF上,Q在ED上时,则当BP=DQ时,四边形APCQ为平行四边形,即8-5t=4t-4, t=.
情况三:当P在AB上,Q在ED上时,四边形APCQ显然不可能为平行四边形;
情况四:当P在AB上,Q在EC上时,四边形APCQ显然不可能为平行四边形.
∴当t=时,四边形APCQ为平行四边形.
②解:a+b=12.
1
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
