2021-2022学年冀教版九年级数学下册第二十九章直线与圆的位置关系单元检测(Word版含答案)
文档属性
| 名称 | 2021-2022学年冀教版九年级数学下册第二十九章直线与圆的位置关系单元检测(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 293.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-20 17:27:10 | ||
图片预览

文档简介
第二十九章 直线与圆的位置关系单元检测
一、单选题
1.已知的半径为3cm,点在内,则不可能等于( )
A.1cm B.1.5cm C.2cm D.3cm
2.在数轴上,点A所表示实数为5,点B所表示实数为a,⊙A半径为3.下列说法中不正确的是( )
A.当a>8时,点B在⊙A外 B.当a<8时,点B在⊙A内
C.当a<2时,点B在⊙A外 D.当2<a<8时,点B在⊙A内
3.在平面直角坐标系中,点的坐标为,若圆与轴相切,那么与直线的位置关系是( )
A.相交 B.相切 C.相离 D.不能确定
4.如图,在平面直角坐标系中,半径为2的⊙P的圆心P的坐标为(﹣3,0),将⊙P沿x轴正方向平移,使⊙P与y轴相切,则平移的距离为( )
A.1或5 B.1或3 C.3或5 D.1
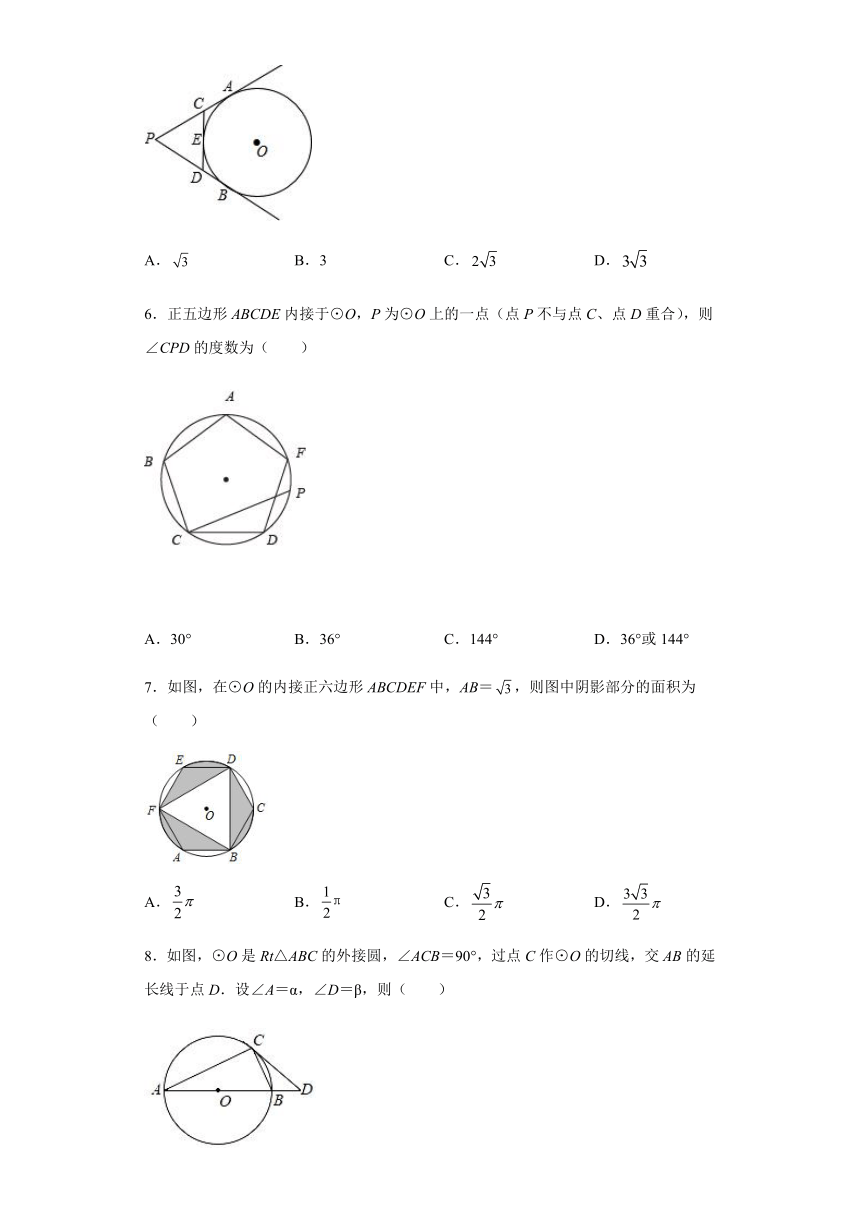
5.如图,分别切于两点,切于点E,交于点.若的周长等于,则线段的长是( )
A. B.3 C. D.
6.正五边形ABCDE内接于⊙O,P为⊙O上的一点(点P不与点C、点D重合),则∠CPD的度数为( )
A.30° B.36° C.144° D.36°或144°
7.如图,在⊙O的内接正六边形ABCDEF中,AB=,则图中阴影部分的面积为( )
A. B. C. D.
8.如图,⊙O是Rt△ABC的外接圆,∠ACB=90°,过点C作⊙O的切线,交AB的延长线于点D.设∠A=α,∠D=β,则( )
A.α﹣β=90° B.α+β=90° C.2α+β=90° D.α+2β=90°
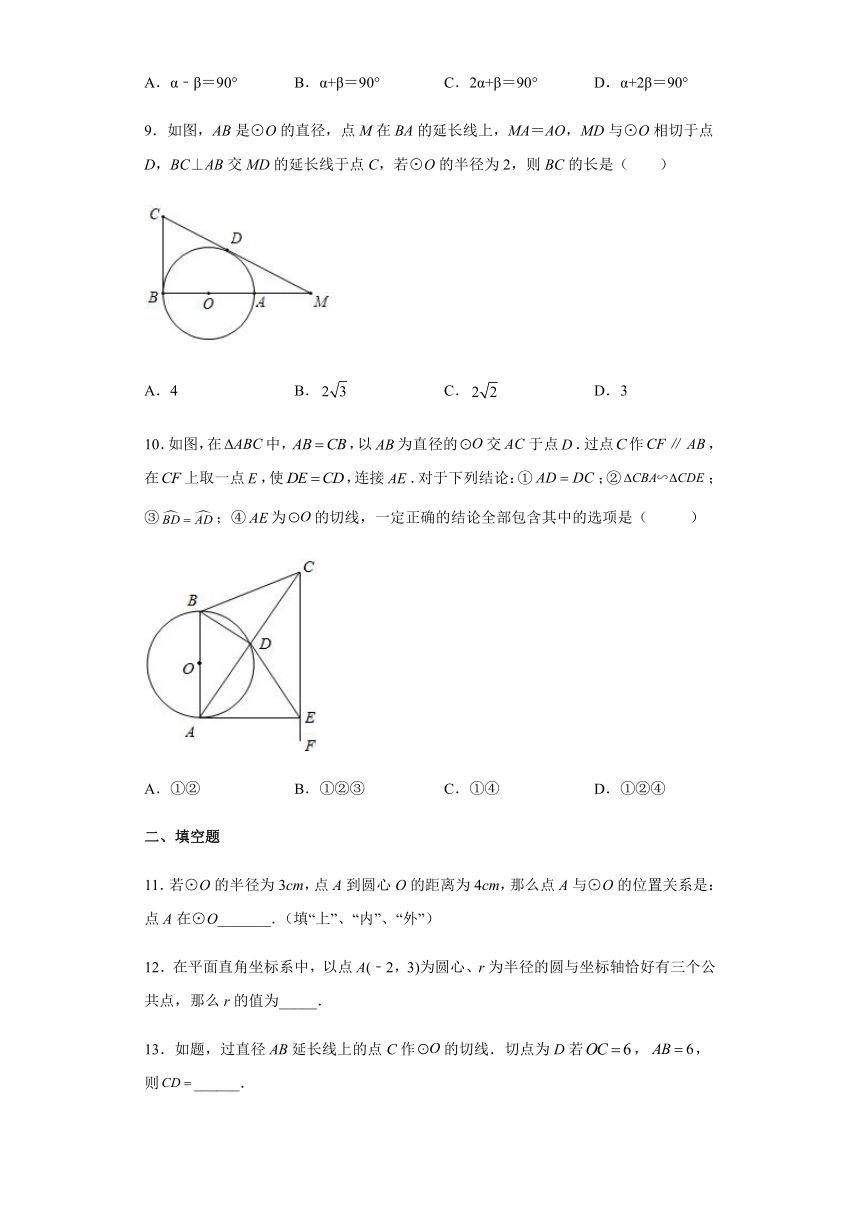
9.如图,AB是⊙O的直径,点M在BA的延长线上,MA=AO,MD与⊙O相切于点D,BC⊥AB交MD的延长线于点C,若⊙O的半径为2,则BC的长是( )
A.4 B. C. D.3
10.如图,在中,,以为直径的交于点.过点作,在上取一点,使,连接.对于下列结论:①;②;③;④为的切线,一定正确的结论全部包含其中的选项是( )
A.①② B.①②③ C.①④ D.①②④
二、填空题
11.若⊙O的半径为3cm,点A到圆心O的距离为4cm,那么点A与⊙O的位置关系是:点A在⊙O_______.(填“上”、“内”、“外”)
12.在平面直角坐标系中,以点A(﹣2,3)为圆心、r为半径的圆与坐标轴恰好有三个公共点,那么r的值为_____.
13.如题,过直径AB延长线上的点C作的切线.切点为D若,,则______.
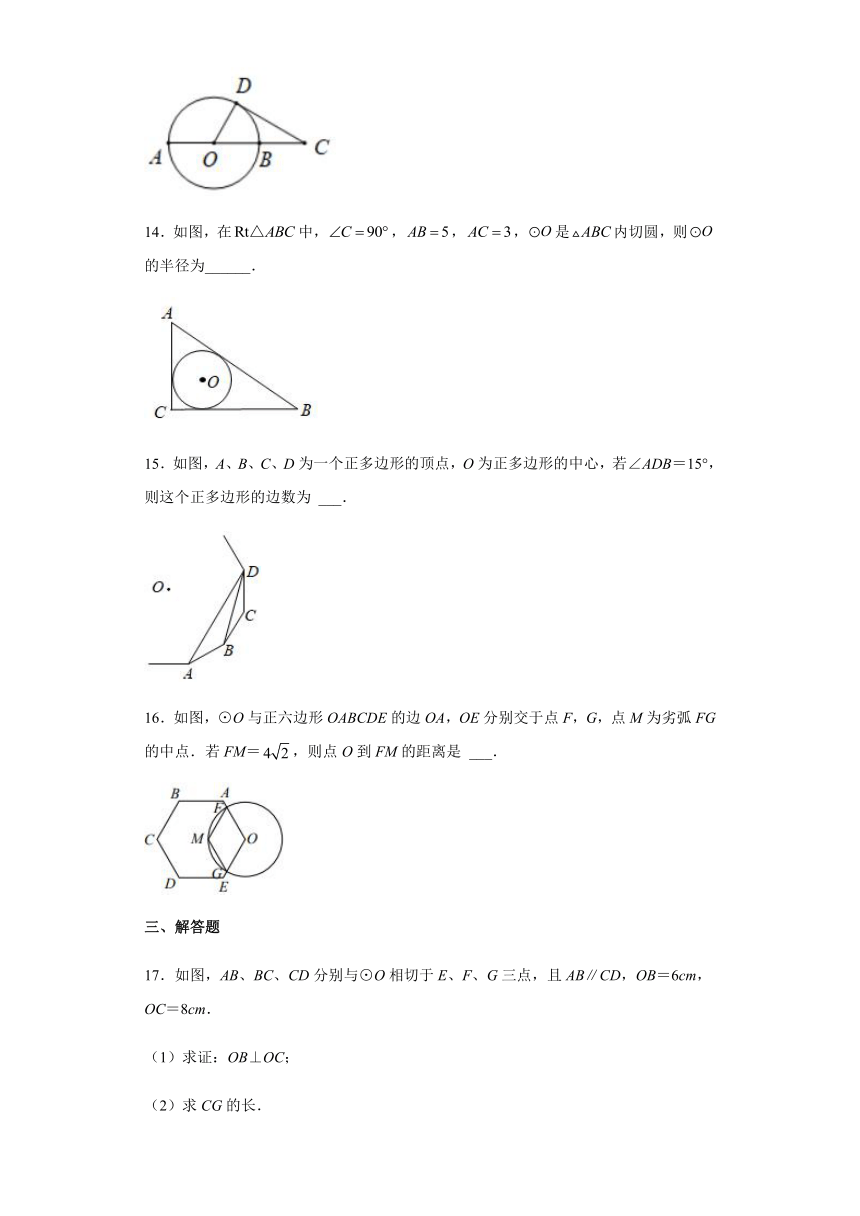
14.如图,在中,,,,是内切圆,则的半径为______.
15.如图,A、B、C、D为一个正多边形的顶点,O为正多边形的中心,若∠ADB=15°,则这个正多边形的边数为 ___.
16.如图,⊙O与正六边形OABCDE的边OA,OE分别交于点F,G,点M为劣弧FG的中点.若FM=,则点O到FM的距离是 ___.
三、解答题
17.如图,AB、BC、CD分别与⊙O相切于E、F、G三点,且AB∥CD,OB=6cm,OC=8cm.
(1)求证:OB⊥OC;
(2)求CG的长.
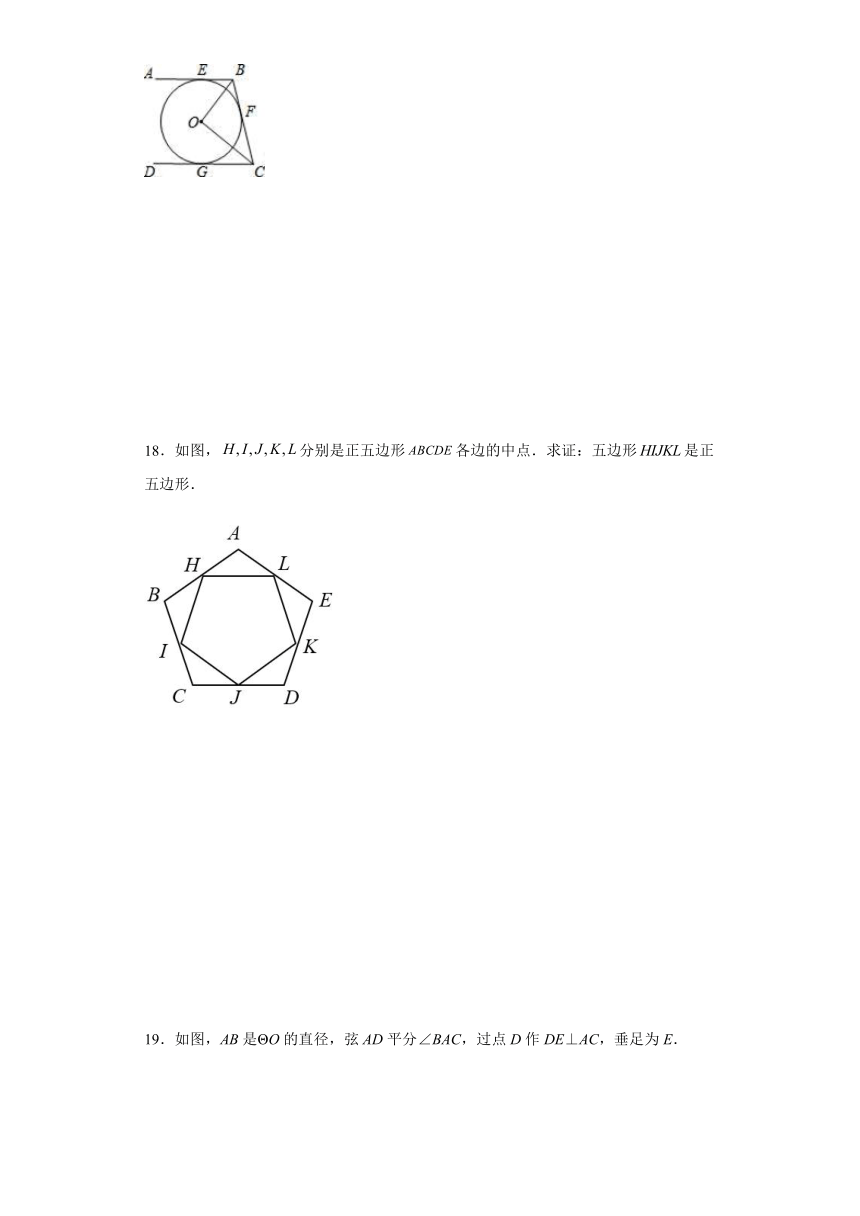
18.如图,分别是正五边形各边的中点.求证:五边形是正五边形.
19.如图,AB是ΘO的直径,弦AD平分∠BAC,过点D作DE⊥AC,垂足为E.
(1)判断DE所在直线与ΘO的位置关系,并说明理由;
(2)若AE=4,ED=2,求ΘO的半径.
20.如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,DE⊥AD,交AB于点E,AE为⊙O的直径
(1)求证:BC与⊙O相切;
(2)若cosB=,AE=4,求CD.
(3)若AC=6,BC=8,求△BDE的面积.
试卷第1页,共3页
答案
1.D
2.B
3.A
4.A
5.A
6.B
7.A
8.C
9.B
10.D
11.外
12.3或
13.
14.1
15.十二
16.
17.解:(1)连接OF;根据切线长定理得:BE=BF,CF=CG,∠OBF=∠OBE,∠OCF=∠OCG;
∵AB∥CD,
∴∠ABC+∠BCD=180°,
∴∠OBE+∠OCF=90°,
∴∠BOC=90°,
∴OB⊥OC;
(2)由(Ⅰ)知,∠BOC=90°.
∵OB=6cm,OC=8cm,
∴由勾股定理得到:BC==10cm,
∴ 即
∴OF=4.8cm.
∴ =6.4cm,
∵CF、CG分别与⊙O相切于F、G,
∴CG=CF=6.4cm.
18.证明:∵五边形ABCDE是正五边形,
∴AB=BC=CD=DE=AE,∠A=∠B=∠C=∠D=∠E,
又∵H,I,J,K,L分别是各边的中点,
∴AH=HB=BI=IC=CJ=JD =DK=KE=EL=AL.
∴△AHL≌△BIH≌△CIJ≌△DJK≌△ELK(SAS),
∴HL=LK=KJ=JI=IH,∠AHL=∠BIH=∠CJI=∠DKJ=∠ELK,∠ALH=∠BHI=∠CIJ=∠DJK=∠EKL,
∵180°-∠AHL-∠ALH=180°-∠BIH-∠BHI=180°-∠CJI-∠CIJ=180°-∠DKJ-∠DJK=180°-∠ELK-∠EKL,
∴∠LHI=∠HIJ=∠IJK=∠JKL=∠KLH,
∴五边形HIJKL是正五边形.
19.(1)解:所在直线与相切.
理由:连接.
∵,
∴.
∵平分,
∴.
∴.
∴.
∴.
∵,
∴.
∴.
∴.
∵是半径,
∴所在直线与相切.
(2)解:连接.
∵是的直径,
∴.
∴.
又∵,
∴.
∴.
∵,,,
∴.
∴.
∴的半径为.
20.(1)证明:如图连接OD.
∵DE⊥AD,AE为⊙O的直径
∴△ADE是直角三角形
∴OD=OA=OE,
∴点D在⊙O上
∴∠OAD=∠ODA
∵AD平分∠CAB,
∴∠CAD=∠DAB,
∴∠CAD=∠ADO,
∴AC∥OD,
∵AC⊥BC,
∴OD⊥BC.
∴BC是⊙O的切线.
(2)解:在Rt△ODB中,
∵cosB==,
设BD=2 k,OB=3k,
∵OD2+BD2=OB2,
∴4+8k2=9k2,
∴k=2,
∴BO=6,BD= ,
∵DO∥AC,
∴=,
∴=,
∴CD=.
(3)解:在Rt△ACB中,AC=6,BC=8,
∴根据勾股定理得:AB=10,
设OD=OA=OE=x,则OB=10-x,
∵AC∥OD,△ACB∽△ODB,
∴,
∴= ,
解得:x= ,
∴OD= ,BE=10-2x=10- = ,
∵= ,即= ,
∴BD=5,
过E作EH⊥BD,
∵EH∥OD,
∴△BEH∽△BOD,
∴= ,
∴EH= ,
∴S△BDE=BD EH=.
答案第1页,共2页
一、单选题
1.已知的半径为3cm,点在内,则不可能等于( )
A.1cm B.1.5cm C.2cm D.3cm
2.在数轴上,点A所表示实数为5,点B所表示实数为a,⊙A半径为3.下列说法中不正确的是( )
A.当a>8时,点B在⊙A外 B.当a<8时,点B在⊙A内
C.当a<2时,点B在⊙A外 D.当2<a<8时,点B在⊙A内
3.在平面直角坐标系中,点的坐标为,若圆与轴相切,那么与直线的位置关系是( )
A.相交 B.相切 C.相离 D.不能确定
4.如图,在平面直角坐标系中,半径为2的⊙P的圆心P的坐标为(﹣3,0),将⊙P沿x轴正方向平移,使⊙P与y轴相切,则平移的距离为( )
A.1或5 B.1或3 C.3或5 D.1
5.如图,分别切于两点,切于点E,交于点.若的周长等于,则线段的长是( )
A. B.3 C. D.
6.正五边形ABCDE内接于⊙O,P为⊙O上的一点(点P不与点C、点D重合),则∠CPD的度数为( )
A.30° B.36° C.144° D.36°或144°
7.如图,在⊙O的内接正六边形ABCDEF中,AB=,则图中阴影部分的面积为( )
A. B. C. D.
8.如图,⊙O是Rt△ABC的外接圆,∠ACB=90°,过点C作⊙O的切线,交AB的延长线于点D.设∠A=α,∠D=β,则( )
A.α﹣β=90° B.α+β=90° C.2α+β=90° D.α+2β=90°
9.如图,AB是⊙O的直径,点M在BA的延长线上,MA=AO,MD与⊙O相切于点D,BC⊥AB交MD的延长线于点C,若⊙O的半径为2,则BC的长是( )
A.4 B. C. D.3
10.如图,在中,,以为直径的交于点.过点作,在上取一点,使,连接.对于下列结论:①;②;③;④为的切线,一定正确的结论全部包含其中的选项是( )
A.①② B.①②③ C.①④ D.①②④
二、填空题
11.若⊙O的半径为3cm,点A到圆心O的距离为4cm,那么点A与⊙O的位置关系是:点A在⊙O_______.(填“上”、“内”、“外”)
12.在平面直角坐标系中,以点A(﹣2,3)为圆心、r为半径的圆与坐标轴恰好有三个公共点,那么r的值为_____.
13.如题,过直径AB延长线上的点C作的切线.切点为D若,,则______.
14.如图,在中,,,,是内切圆,则的半径为______.
15.如图,A、B、C、D为一个正多边形的顶点,O为正多边形的中心,若∠ADB=15°,则这个正多边形的边数为 ___.
16.如图,⊙O与正六边形OABCDE的边OA,OE分别交于点F,G,点M为劣弧FG的中点.若FM=,则点O到FM的距离是 ___.
三、解答题
17.如图,AB、BC、CD分别与⊙O相切于E、F、G三点,且AB∥CD,OB=6cm,OC=8cm.
(1)求证:OB⊥OC;
(2)求CG的长.
18.如图,分别是正五边形各边的中点.求证:五边形是正五边形.
19.如图,AB是ΘO的直径,弦AD平分∠BAC,过点D作DE⊥AC,垂足为E.
(1)判断DE所在直线与ΘO的位置关系,并说明理由;
(2)若AE=4,ED=2,求ΘO的半径.
20.如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,DE⊥AD,交AB于点E,AE为⊙O的直径
(1)求证:BC与⊙O相切;
(2)若cosB=,AE=4,求CD.
(3)若AC=6,BC=8,求△BDE的面积.
试卷第1页,共3页
答案
1.D
2.B
3.A
4.A
5.A
6.B
7.A
8.C
9.B
10.D
11.外
12.3或
13.
14.1
15.十二
16.
17.解:(1)连接OF;根据切线长定理得:BE=BF,CF=CG,∠OBF=∠OBE,∠OCF=∠OCG;
∵AB∥CD,
∴∠ABC+∠BCD=180°,
∴∠OBE+∠OCF=90°,
∴∠BOC=90°,
∴OB⊥OC;
(2)由(Ⅰ)知,∠BOC=90°.
∵OB=6cm,OC=8cm,
∴由勾股定理得到:BC==10cm,
∴ 即
∴OF=4.8cm.
∴ =6.4cm,
∵CF、CG分别与⊙O相切于F、G,
∴CG=CF=6.4cm.
18.证明:∵五边形ABCDE是正五边形,
∴AB=BC=CD=DE=AE,∠A=∠B=∠C=∠D=∠E,
又∵H,I,J,K,L分别是各边的中点,
∴AH=HB=BI=IC=CJ=JD =DK=KE=EL=AL.
∴△AHL≌△BIH≌△CIJ≌△DJK≌△ELK(SAS),
∴HL=LK=KJ=JI=IH,∠AHL=∠BIH=∠CJI=∠DKJ=∠ELK,∠ALH=∠BHI=∠CIJ=∠DJK=∠EKL,
∵180°-∠AHL-∠ALH=180°-∠BIH-∠BHI=180°-∠CJI-∠CIJ=180°-∠DKJ-∠DJK=180°-∠ELK-∠EKL,
∴∠LHI=∠HIJ=∠IJK=∠JKL=∠KLH,
∴五边形HIJKL是正五边形.
19.(1)解:所在直线与相切.
理由:连接.
∵,
∴.
∵平分,
∴.
∴.
∴.
∴.
∵,
∴.
∴.
∴.
∵是半径,
∴所在直线与相切.
(2)解:连接.
∵是的直径,
∴.
∴.
又∵,
∴.
∴.
∵,,,
∴.
∴.
∴的半径为.
20.(1)证明:如图连接OD.
∵DE⊥AD,AE为⊙O的直径
∴△ADE是直角三角形
∴OD=OA=OE,
∴点D在⊙O上
∴∠OAD=∠ODA
∵AD平分∠CAB,
∴∠CAD=∠DAB,
∴∠CAD=∠ADO,
∴AC∥OD,
∵AC⊥BC,
∴OD⊥BC.
∴BC是⊙O的切线.
(2)解:在Rt△ODB中,
∵cosB==,
设BD=2 k,OB=3k,
∵OD2+BD2=OB2,
∴4+8k2=9k2,
∴k=2,
∴BO=6,BD= ,
∵DO∥AC,
∴=,
∴=,
∴CD=.
(3)解:在Rt△ACB中,AC=6,BC=8,
∴根据勾股定理得:AB=10,
设OD=OA=OE=x,则OB=10-x,
∵AC∥OD,△ACB∽△ODB,
∴,
∴= ,
解得:x= ,
∴OD= ,BE=10-2x=10- = ,
∵= ,即= ,
∴BD=5,
过E作EH⊥BD,
∵EH∥OD,
∴△BEH∽△BOD,
∴= ,
∴EH= ,
∴S△BDE=BD EH=.
答案第1页,共2页
