高中数学新教材苏教版(2019)必修第二册11.2正弦定理知识点与题型归纳
文档属性
| 名称 | 高中数学新教材苏教版(2019)必修第二册11.2正弦定理知识点与题型归纳 |

|
|
| 格式 | docx | ||
| 文件大小 | 781.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-21 08:05:14 | ||
图片预览




文档简介
11.2正弦定理的知识点与题型归纳
知识点
(一)正弦定理及其变形
正弦定理:在一个三角形中各边和它所对角的正弦比相等,即:
定理的变形:(1).
(2)化边为角:;
(3)化边为角:
(4)化角为边:
(5)化角为边:
【要点诠释】:
(1)正弦定理适合于任何三角形,且(为三角形的外接圆半径);
(2)定理等价于,,,每个等式可视为一个方程,知三求一.
(3)解决的题型:①已知两角和一边,求其它; ②已知两边和一边的对角,求其它;
(4)在已知两边和一边的对角,求其它的类型中,可能出现无解、一解或两解,应结合“三角形中大边对大角”定理及几何作图来帮助理解;
(5)正弦定理的主要作用是方程和分式中的边角互化.其原则为关于边或角的正弦值是否具备齐次的特征.如果齐次则可直接进行边化角或是角化边,否则不可行;
例如:①
②(恒等式)
③ .
(二)正弦定理的推导
法一:作高法
不妨设∠C为最大角,
(1)若∠C为直角,
有, , ,
即:,,,
所以.
(2)若∠C为锐角,过点A作AC⊥BC于D,
此时有,,所以csinB=bsinC,
即,同理,所以.
若∠C为钝角,过点A作AC⊥BC,交BC延长线于D,此时有,且,故可得;
由(1)(2)(3)知,结论成立.
法二:向量法
在△ABC中,设∠C最大,有,过A作AD垂直BC于D,
于是,
即,
当∠C为锐角或直角时,;当∠C为钝角时,;
所以csinB-bsinC=0,即,同理,所以.
法三:圆转化法
(1)当为锐角三角形时
如图,圆O是的外接圆,直径为,则,
所以,
所以(为的外接圆半径)
同理:,
故:
(2)当为钝角三角形时
如图,.易证.
法四:面积法
任意斜中,如图作,则
同理:,
故,两边同除以
即得:
(三)三角形的面积公式及证明
1.三角形的面积公式
(1),其中为边上的高
(2)
(3)海伦公式 ,其中
(4),其中是三角形内切圆半径.
(5),R为外接圆半径
2.(1)运用三角形的面积证明正弦定理(见上)
(2)利用三角形的面积证明三角函数的和与差公式
根据三角形面积公式,有,
所以,
因为,
所以,
因为,所以.
根据此式和诱导公式,可证出其它和角公式及差角公式.
;
;
[3].
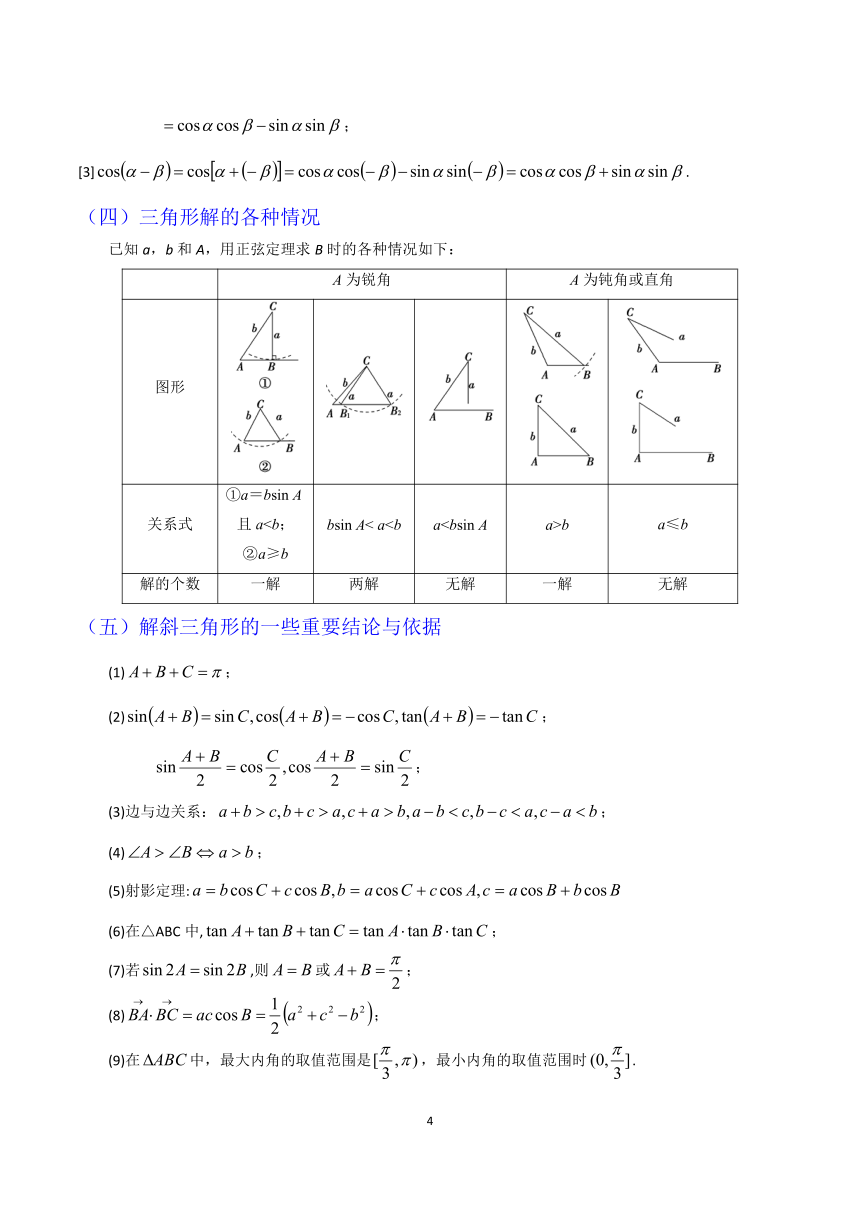
(四)三角形解的各种情况
已知a,b和A,用正弦定理求B时的各种情况如下:
A为锐角 A为钝角或直角
图形
关系式 ①a=bsin A且ab a≤b
解的个数 一解 两解 无解 一解 无解
(五)解斜三角形的一些重要结论与依据
(1);
(2);
;
(3)边与边关系:;
(4);
(5)射影定理:
(6)在△ABC中,;
(7)若,则或;
(8);
(9)在中,最大内角的取值范围是,最小内角的取值范围时.
二、典型例题
类型一:正弦定理的简单应用
【例1】.中,,BC=3,则的周长为( )
A. B.C. D.
【解析】:由正弦定理得:,
得b+c=[sinB+sin(-B)]=.
故三角形的周长为:3+b+c=,故选D.
【例2】.在,求:和,.
【解析】:由正弦定理得:,所以,
(法一)因为, 所以或,
当时,,(舍去);
当时,,所以.
(法二)因为,, 所以,
所以即为锐角, 所以,
所以.
类型二:正弦定理的综合运用
【例3】.(2018 湖南高考)设的内角A,B,C的对边分别为a,b,c,,且B为钝角.
(1)证明:
(2)求的取值范围.
【解析】:(1)由a=btanA及正弦定理,得,
所以sinB=cosA,即sinB=sin(+A).
又B为钝角,因此+A(,A),故B=+A,即B-A=;
由(I)知,C=-(A+B)=-(2A+)=-2A>0,所以A,
于是sinA+sinC=sinA+sin(-2A)= sinA+cos2A=-2A+sinA+1 =-2(sinA-)+,
因为0由此可知sinA+sinC的取值范围是(,].
【例4】.(2018浙江文)在△ABC中,内角A,B,C所对的边分别为a,b,c.已知b+c=2acos B.
(Ⅰ)证明:A=2B;
(Ⅱ)若cos B=,求cos C的值.
【解析】:(1)由正弦定理得,
故,
于是,
又,故,所以或,
因此(舍去)或,
所以.
(2)由,得,,
故,,
.
类型三:利用正弦定理判断三角形的形状
【例5】.在中,若试判断的形状.
【解析】:由已知条件及正弦定理可得,
因为A,B为三角形的内角,所以,,
所以,所以A=B或,
所以为等腰三角形或直角三角形.
【例6】.在△ABC中,试判断三角形的形状
【解析】:(法一)利用正弦定理化边为角.
因为,又,所以,
所以,所以,
因为0<A,B<π,所以-π<A-B<π,所以,即,
故此三角形是等腰三角形.
(法二)利用余弦定理化角为边
因为,又,,
所以,因为,所以.
故此三角形是等腰三角形.
类型四:正弦定理在几何中的应用
【例7】.在△ABC中,AD是∠BAC的平分线,如图所示,用正弦定理证明:=.
【证明】:设,,.
在△ABD和△ACD中分别运用正弦定理,得,,
又,所以=,即=.
【例8】.(2018 新课标Ⅱ文)△ABC中D是BC上的点,AD平分BAC,BD=2DC.
(I)求 ;
(II)若,求.
【解析】:(Ⅰ)由正弦定理得
因为AD平分∠BAC,BD=2DC,所以
(Ⅱ)因为∠C=180°-(∠BAC+∠B),∠BAC=60°,
所以
由(Ⅰ)知2sin∠B=sin∠C,所以,∠B=30°.
三、巩固练习
1.已知△ABC的三个内角A,B,C的对边边长分别为a,b,c,若2a=3b,A=2B,则cosB=( )
A. B. C. D.0
2.在△ABC中,a=,b=,A=30°,则c等于( )
A.2 B. C.2或 D.以上都不对
3.以下关于正弦定理的叙述或变形错误的是( )
A.在△ABC中,a∶b∶c=sin A∶sin B∶sin C
B.在△ABC中,若sin 2A=sin 2B,则a=b
C.在△ABC中,若sin A>sin B,则A>B;若A>B,则sin A>sin B都成立
D.在△ABC中,=
4.若==,则△ABC是( )
A.等边三角形 B.直角三角形,且有一个角是30°
C.等腰直角三角形 D.等腰三角形,且有一个角是30°
5. 已知△ABC中,角A,B,C的对边分别是a,b,c,若 ,则△ABC是( )
A.等边三角形 B.锐角三角形 C.等腰直角三角形 D.钝角三角形
6.在△ABC中,已知B=2A,∠ACB的平分线CD把三角形分成面积为4:3的两部分,则( )
7. 在△ABC中,内角A,B,C所对的边分别为a,b,c,已知bsinAacosB=2bc,则A=( )
A. B. C. D.
8. △ABC的内角A,B,C的对边分别为a,b,c,已知,则A的大小为 .
9.在中,,,,则的外接圆面积为 .
10.已知中,,,若仅有一解,则 .
11.已知分别为的三个内角的对边,已知,,,若满足条件的三角形有两个,则的取值范围是 .
12.在△ABC中,A=60°,a=,则等于 .
13.在中,内角对应的边分别为,已知,,且,则的面积为 .
14.在△ABC中,内角A,B,C的对边分别为a,b,c,且,则角的大小为 .
15.在ABC中,B=,AB=,A的角平分线AD=,则AC=_______.
16.(2018新课标Ⅰ卷)在平面四边形ABCD中,∠A=∠B=∠C=75°,BC=2,则AB的取值范围是 .
17. 在△ABC中,a=x,b=2,B=45°,若△ABC只有一解,则x的取值集合为________.
18. 在中,求B及C.
19.在△ABC中,角A,B,C的对边分别为a,b,c,且,.
(1)求角C的大小;
(2)求 的最大值.
20.如图,D是直角△ABC斜边BC上一点,AB=AD,记∠CAD=,∠ABC=.
(1)证明 ;
(2)若AC=DC,求的值.
21. (2018浙江高考文)在△ABC中,内角A,B,C所对的边分别为a,b,c.已知.
(1)求的值;
(2)若,求△ABC的面积.
答案与解析
1. 【解答】:因为2a=3b,所以根据正弦定理得2sinA=3sinB,且A=2B,
所以2sin2B=4sinBcosB=3sinB,且sinB≠0,所以.故选:B.
2. 【解析】:由于sin B==,故B=60°或120°.
当B=60°时,C=90°时,c=30°.c==2;
当B=120°时,C=30°,c=a=.故选:C
3. 【解析】:由正弦定理知A、C、D正确,
而sin 2A=sin 2B,可得A=B或2A+2B=π,所以a=b或a2+b2=c2,故B错误.
4. 【解析】:在△ABC中,由正弦定理:a=2Rsin A,b=2Rsin B,c=2Rsin C,代入==得:
==,所以==1.所以tan B=tan C=1,所以B=C=45°.
所以△ABC是等腰直角三角形.故选:C
5. 【解析】:因为,所以由正弦定理可得:,而,当且仅当 时取等号.所以,即 ,又 ,故可得:
所以.
又因为,可得,
故三角形为等腰三角形,故选:C
6.【解析】:由角平分线定理得:,由正弦定理:,及B=2A,得:,
所以,故选A.
7.【解答】:因为bsinAacosB=2bc,
所以由正弦定理可得:sinBsinAsinAcosB=2sinBsinC,
所以sinBsinAsinAcosB=2sinBsinC=2sinB(sinAcosB+cosAsinB),
所以sinBsinA=2sinBcosAsinB,
又因为sinB≠0,所以sinAcosA=2,所以2sin(A)=2,可得A2kπ,k∈Z,
又A∈(0,π),所以A.故选:C.
8.【解答】:因为,
所以由正弦定理可得:(sinAcosC﹣sinCcosA)=sinB,可得:sin(A﹣C)=sinB,
所以sin(A﹣C),
因为A+C=120°,又因为0°<A<120°,0°<C<120°,可得:﹣120°<A﹣C<120°,
所以A﹣C=30°,解得:A=75°.故答案为:75°.
9.【解析】:因为在中,,,所以,
又,设三角形外接圆半径为,则,
因此的外接圆面积为.
10.【解析】:由题中已知中,,,则角所对的高线长可表示为,因为三角形形状唯一,所以三角形为直角三角形或钝角三角形,则 或, 所以 或,故答案为
11.【解析】:在中,由,,,则,
要使得三角形有两个,则满足,即, 解得,实数范围是
12.【解析】:由正弦定理,==
所以a=sinA,b=sinB,c=sinC
则==
13.【解析】:因为,,,所以由正弦定理得,即,
得,因为,所以所以,
所以面积
14.【解析】:由已知,根据正弦定理得:,则,即,所以.故答案为.
15.【解析】:由正弦定理得,即,解得,
,从而,所以,
.
16.【解析】:如图所示,延长BA,CD交于E,平移AD,当A与D重合与E点时,AB最长,在△BCE中,∠B=∠C=75°,∠E=30°,BC=2,由正弦定理可得,即,
解得=,平移AD ,当D与C重合时,AB最短,此时与AB交于F,
在△BCF中,∠B=∠BFC=75°,∠FCB=30°,由正弦定理知,,即,解得BF=,
所以AB的取值范围为(,).
17. 【解析】:,
当x=2时,sin A=1,△ABC有一解;
又当a≤b时,即x≤2时,A为锐角,△ABC只有一解.故答案为: {x|018. 【解析】:由正弦定理得,
因为且,所以B有两解,得或,所以或
19. 【解析】:(1) ,即,则
因为,又,进而,所以,故 故
(2)由正弦定理及(1)得
= ,故当 取到最大值2.
20.【解析】:(1).如图,因为,
即.
(2)在中,由正弦定理得
由(1)得,所以
即.
因为,所以.
21. 【解析】:(1)由,得,
所以.
(2)由可得,.a=3,,由正弦定理知:.
又,
所以.
1
知识点
(一)正弦定理及其变形
正弦定理:在一个三角形中各边和它所对角的正弦比相等,即:
定理的变形:(1).
(2)化边为角:;
(3)化边为角:
(4)化角为边:
(5)化角为边:
【要点诠释】:
(1)正弦定理适合于任何三角形,且(为三角形的外接圆半径);
(2)定理等价于,,,每个等式可视为一个方程,知三求一.
(3)解决的题型:①已知两角和一边,求其它; ②已知两边和一边的对角,求其它;
(4)在已知两边和一边的对角,求其它的类型中,可能出现无解、一解或两解,应结合“三角形中大边对大角”定理及几何作图来帮助理解;
(5)正弦定理的主要作用是方程和分式中的边角互化.其原则为关于边或角的正弦值是否具备齐次的特征.如果齐次则可直接进行边化角或是角化边,否则不可行;
例如:①
②(恒等式)
③ .
(二)正弦定理的推导
法一:作高法
不妨设∠C为最大角,
(1)若∠C为直角,
有, , ,
即:,,,
所以.
(2)若∠C为锐角,过点A作AC⊥BC于D,
此时有,,所以csinB=bsinC,
即,同理,所以.
若∠C为钝角,过点A作AC⊥BC,交BC延长线于D,此时有,且,故可得;
由(1)(2)(3)知,结论成立.
法二:向量法
在△ABC中,设∠C最大,有,过A作AD垂直BC于D,
于是,
即,
当∠C为锐角或直角时,;当∠C为钝角时,;
所以csinB-bsinC=0,即,同理,所以.
法三:圆转化法
(1)当为锐角三角形时
如图,圆O是的外接圆,直径为,则,
所以,
所以(为的外接圆半径)
同理:,
故:
(2)当为钝角三角形时
如图,.易证.
法四:面积法
任意斜中,如图作,则
同理:,
故,两边同除以
即得:
(三)三角形的面积公式及证明
1.三角形的面积公式
(1),其中为边上的高
(2)
(3)海伦公式 ,其中
(4),其中是三角形内切圆半径.
(5),R为外接圆半径
2.(1)运用三角形的面积证明正弦定理(见上)
(2)利用三角形的面积证明三角函数的和与差公式
根据三角形面积公式,有,
所以,
因为,
所以,
因为,所以.
根据此式和诱导公式,可证出其它和角公式及差角公式.
;
;
[3].
(四)三角形解的各种情况
已知a,b和A,用正弦定理求B时的各种情况如下:
A为锐角 A为钝角或直角
图形
关系式 ①a=bsin A且a
解的个数 一解 两解 无解 一解 无解
(五)解斜三角形的一些重要结论与依据
(1);
(2);
;
(3)边与边关系:;
(4);
(5)射影定理:
(6)在△ABC中,;
(7)若,则或;
(8);
(9)在中,最大内角的取值范围是,最小内角的取值范围时.
二、典型例题
类型一:正弦定理的简单应用
【例1】.中,,BC=3,则的周长为( )
A. B.C. D.
【解析】:由正弦定理得:,
得b+c=[sinB+sin(-B)]=.
故三角形的周长为:3+b+c=,故选D.
【例2】.在,求:和,.
【解析】:由正弦定理得:,所以,
(法一)因为, 所以或,
当时,,(舍去);
当时,,所以.
(法二)因为,, 所以,
所以即为锐角, 所以,
所以.
类型二:正弦定理的综合运用
【例3】.(2018 湖南高考)设的内角A,B,C的对边分别为a,b,c,,且B为钝角.
(1)证明:
(2)求的取值范围.
【解析】:(1)由a=btanA及正弦定理,得,
所以sinB=cosA,即sinB=sin(+A).
又B为钝角,因此+A(,A),故B=+A,即B-A=;
由(I)知,C=-(A+B)=-(2A+)=-2A>0,所以A,
于是sinA+sinC=sinA+sin(-2A)= sinA+cos2A=-2A+sinA+1 =-2(sinA-)+,
因为0
【例4】.(2018浙江文)在△ABC中,内角A,B,C所对的边分别为a,b,c.已知b+c=2acos B.
(Ⅰ)证明:A=2B;
(Ⅱ)若cos B=,求cos C的值.
【解析】:(1)由正弦定理得,
故,
于是,
又,故,所以或,
因此(舍去)或,
所以.
(2)由,得,,
故,,
.
类型三:利用正弦定理判断三角形的形状
【例5】.在中,若试判断的形状.
【解析】:由已知条件及正弦定理可得,
因为A,B为三角形的内角,所以,,
所以,所以A=B或,
所以为等腰三角形或直角三角形.
【例6】.在△ABC中,试判断三角形的形状
【解析】:(法一)利用正弦定理化边为角.
因为,又,所以,
所以,所以,
因为0<A,B<π,所以-π<A-B<π,所以,即,
故此三角形是等腰三角形.
(法二)利用余弦定理化角为边
因为,又,,
所以,因为,所以.
故此三角形是等腰三角形.
类型四:正弦定理在几何中的应用
【例7】.在△ABC中,AD是∠BAC的平分线,如图所示,用正弦定理证明:=.
【证明】:设,,.
在△ABD和△ACD中分别运用正弦定理,得,,
又,所以=,即=.
【例8】.(2018 新课标Ⅱ文)△ABC中D是BC上的点,AD平分BAC,BD=2DC.
(I)求 ;
(II)若,求.
【解析】:(Ⅰ)由正弦定理得
因为AD平分∠BAC,BD=2DC,所以
(Ⅱ)因为∠C=180°-(∠BAC+∠B),∠BAC=60°,
所以
由(Ⅰ)知2sin∠B=sin∠C,所以,∠B=30°.
三、巩固练习
1.已知△ABC的三个内角A,B,C的对边边长分别为a,b,c,若2a=3b,A=2B,则cosB=( )
A. B. C. D.0
2.在△ABC中,a=,b=,A=30°,则c等于( )
A.2 B. C.2或 D.以上都不对
3.以下关于正弦定理的叙述或变形错误的是( )
A.在△ABC中,a∶b∶c=sin A∶sin B∶sin C
B.在△ABC中,若sin 2A=sin 2B,则a=b
C.在△ABC中,若sin A>sin B,则A>B;若A>B,则sin A>sin B都成立
D.在△ABC中,=
4.若==,则△ABC是( )
A.等边三角形 B.直角三角形,且有一个角是30°
C.等腰直角三角形 D.等腰三角形,且有一个角是30°
5. 已知△ABC中,角A,B,C的对边分别是a,b,c,若 ,则△ABC是( )
A.等边三角形 B.锐角三角形 C.等腰直角三角形 D.钝角三角形
6.在△ABC中,已知B=2A,∠ACB的平分线CD把三角形分成面积为4:3的两部分,则( )
7. 在△ABC中,内角A,B,C所对的边分别为a,b,c,已知bsinAacosB=2bc,则A=( )
A. B. C. D.
8. △ABC的内角A,B,C的对边分别为a,b,c,已知,则A的大小为 .
9.在中,,,,则的外接圆面积为 .
10.已知中,,,若仅有一解,则 .
11.已知分别为的三个内角的对边,已知,,,若满足条件的三角形有两个,则的取值范围是 .
12.在△ABC中,A=60°,a=,则等于 .
13.在中,内角对应的边分别为,已知,,且,则的面积为 .
14.在△ABC中,内角A,B,C的对边分别为a,b,c,且,则角的大小为 .
15.在ABC中,B=,AB=,A的角平分线AD=,则AC=_______.
16.(2018新课标Ⅰ卷)在平面四边形ABCD中,∠A=∠B=∠C=75°,BC=2,则AB的取值范围是 .
17. 在△ABC中,a=x,b=2,B=45°,若△ABC只有一解,则x的取值集合为________.
18. 在中,求B及C.
19.在△ABC中,角A,B,C的对边分别为a,b,c,且,.
(1)求角C的大小;
(2)求 的最大值.
20.如图,D是直角△ABC斜边BC上一点,AB=AD,记∠CAD=,∠ABC=.
(1)证明 ;
(2)若AC=DC,求的值.
21. (2018浙江高考文)在△ABC中,内角A,B,C所对的边分别为a,b,c.已知.
(1)求的值;
(2)若,求△ABC的面积.
答案与解析
1. 【解答】:因为2a=3b,所以根据正弦定理得2sinA=3sinB,且A=2B,
所以2sin2B=4sinBcosB=3sinB,且sinB≠0,所以.故选:B.
2. 【解析】:由于sin B==,故B=60°或120°.
当B=60°时,C=90°时,c=30°.c==2;
当B=120°时,C=30°,c=a=.故选:C
3. 【解析】:由正弦定理知A、C、D正确,
而sin 2A=sin 2B,可得A=B或2A+2B=π,所以a=b或a2+b2=c2,故B错误.
4. 【解析】:在△ABC中,由正弦定理:a=2Rsin A,b=2Rsin B,c=2Rsin C,代入==得:
==,所以==1.所以tan B=tan C=1,所以B=C=45°.
所以△ABC是等腰直角三角形.故选:C
5. 【解析】:因为,所以由正弦定理可得:,而,当且仅当 时取等号.所以,即 ,又 ,故可得:
所以.
又因为,可得,
故三角形为等腰三角形,故选:C
6.【解析】:由角平分线定理得:,由正弦定理:,及B=2A,得:,
所以,故选A.
7.【解答】:因为bsinAacosB=2bc,
所以由正弦定理可得:sinBsinAsinAcosB=2sinBsinC,
所以sinBsinAsinAcosB=2sinBsinC=2sinB(sinAcosB+cosAsinB),
所以sinBsinA=2sinBcosAsinB,
又因为sinB≠0,所以sinAcosA=2,所以2sin(A)=2,可得A2kπ,k∈Z,
又A∈(0,π),所以A.故选:C.
8.【解答】:因为,
所以由正弦定理可得:(sinAcosC﹣sinCcosA)=sinB,可得:sin(A﹣C)=sinB,
所以sin(A﹣C),
因为A+C=120°,又因为0°<A<120°,0°<C<120°,可得:﹣120°<A﹣C<120°,
所以A﹣C=30°,解得:A=75°.故答案为:75°.
9.【解析】:因为在中,,,所以,
又,设三角形外接圆半径为,则,
因此的外接圆面积为.
10.【解析】:由题中已知中,,,则角所对的高线长可表示为,因为三角形形状唯一,所以三角形为直角三角形或钝角三角形,则 或, 所以 或,故答案为
11.【解析】:在中,由,,,则,
要使得三角形有两个,则满足,即, 解得,实数范围是
12.【解析】:由正弦定理,==
所以a=sinA,b=sinB,c=sinC
则==
13.【解析】:因为,,,所以由正弦定理得,即,
得,因为,所以所以,
所以面积
14.【解析】:由已知,根据正弦定理得:,则,即,所以.故答案为.
15.【解析】:由正弦定理得,即,解得,
,从而,所以,
.
16.【解析】:如图所示,延长BA,CD交于E,平移AD,当A与D重合与E点时,AB最长,在△BCE中,∠B=∠C=75°,∠E=30°,BC=2,由正弦定理可得,即,
解得=,平移AD ,当D与C重合时,AB最短,此时与AB交于F,
在△BCF中,∠B=∠BFC=75°,∠FCB=30°,由正弦定理知,,即,解得BF=,
所以AB的取值范围为(,).
17. 【解析】:,
当x=2时,sin A=1,△ABC有一解;
又当a≤b时,即x≤2时,A为锐角,△ABC只有一解.故答案为: {x|0
因为且,所以B有两解,得或,所以或
19. 【解析】:(1) ,即,则
因为,又,进而,所以,故 故
(2)由正弦定理及(1)得
= ,故当 取到最大值2.
20.【解析】:(1).如图,因为,
即.
(2)在中,由正弦定理得
由(1)得,所以
即.
因为,所以.
21. 【解析】:(1)由,得,
所以.
(2)由可得,.a=3,,由正弦定理知:.
又,
所以.
1
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
