2021—2022学年人教版八年级数学下册19.1函数课后练习(Word版含答案)
文档属性
| 名称 | 2021—2022学年人教版八年级数学下册19.1函数课后练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 240.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-20 18:32:56 | ||
图片预览

文档简介
2021——2022学年度人教版八年级数学下册 第十九章 一次函数 19.1函数 课后练习
一、选择题
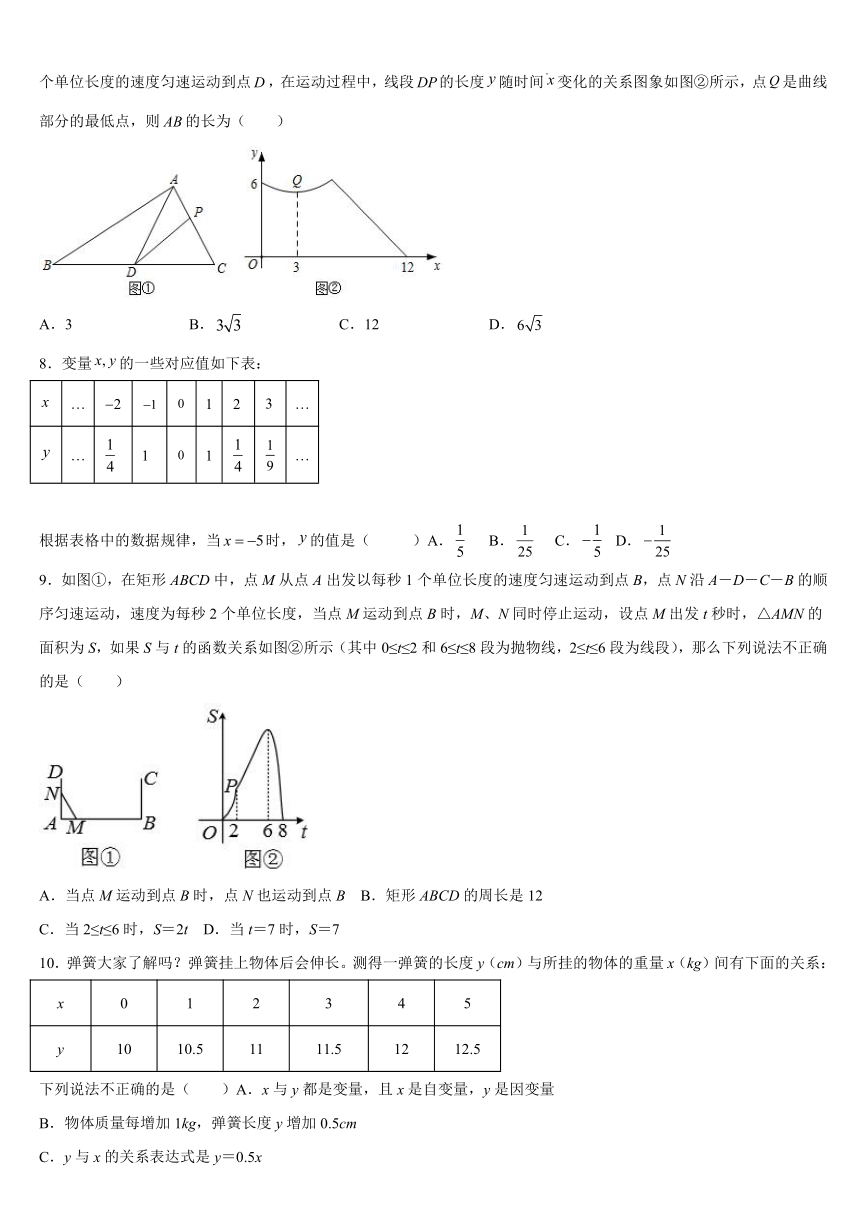
1.下列各曲线中,不表示y是x的函数的是( )
A. B. C. D.
2.已知一个等腰三角形的腰长为x,底边长为y,周长是10,则底边y关于腰长x之间的函数关系式及定义域为( )
A.y=10﹣2x(5<x<10) B.y=10﹣2x(2.5<x<5)
C.y=10﹣2x(0<x<5) D.y=10﹣2x(0<x<10)
3.函数y=中,自变量x的取值范围是( )
A.x≥-1 B.x≥-1且x≠3 C.x≠-1 D.x≠-1且x≠3
4.某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据
温度/℃ ﹣20 ﹣10 0 10 20 30
声速/m/s 318 324 330 336 342 348
下列说法错误的是( )A.这个问题中,空气温度和声速都是变量
B.空气温度每降低10℃,声速减少6m/s
C.当空气温度为20℃时,声音5s可以传播1710m
D.由数据可以推测,在一定范围内,空气温度越高,声速越快
5.将长为,宽为的长方形白纸,按如图所示的方法黏合起来,黏合的部分宽为.当黏合后的纸条总长度为,则需长方形白纸的数量为( )
A.18 B.19 C.20 D.21
6.《龟兔赛跑》是我们非常熟悉的故事.大意是乌龟和兔子赛跑,兔子开始就超过乌龟好远,兔子不耐烦了就在路边睡了一觉,乌龟一直往目的地奔跑,最终乌龟获得了胜利.下面能反映这个故事情节的图像是哪个?( )
A.B.C.D.
7.如图①,在中,,点是边的中点,点从的顶点出发,沿的路线以每秒1个单位长度的速度匀速运动到点,在运动过程中,线段的长度随时间变化的关系图象如图②所示,点是曲线部分的最低点,则的长为( )
A.3 B. C.12 D.
8.变量的一些对应值如下表:
… …
… …
根据表格中的数据规律,当时,的值是( )A. B. C. D.
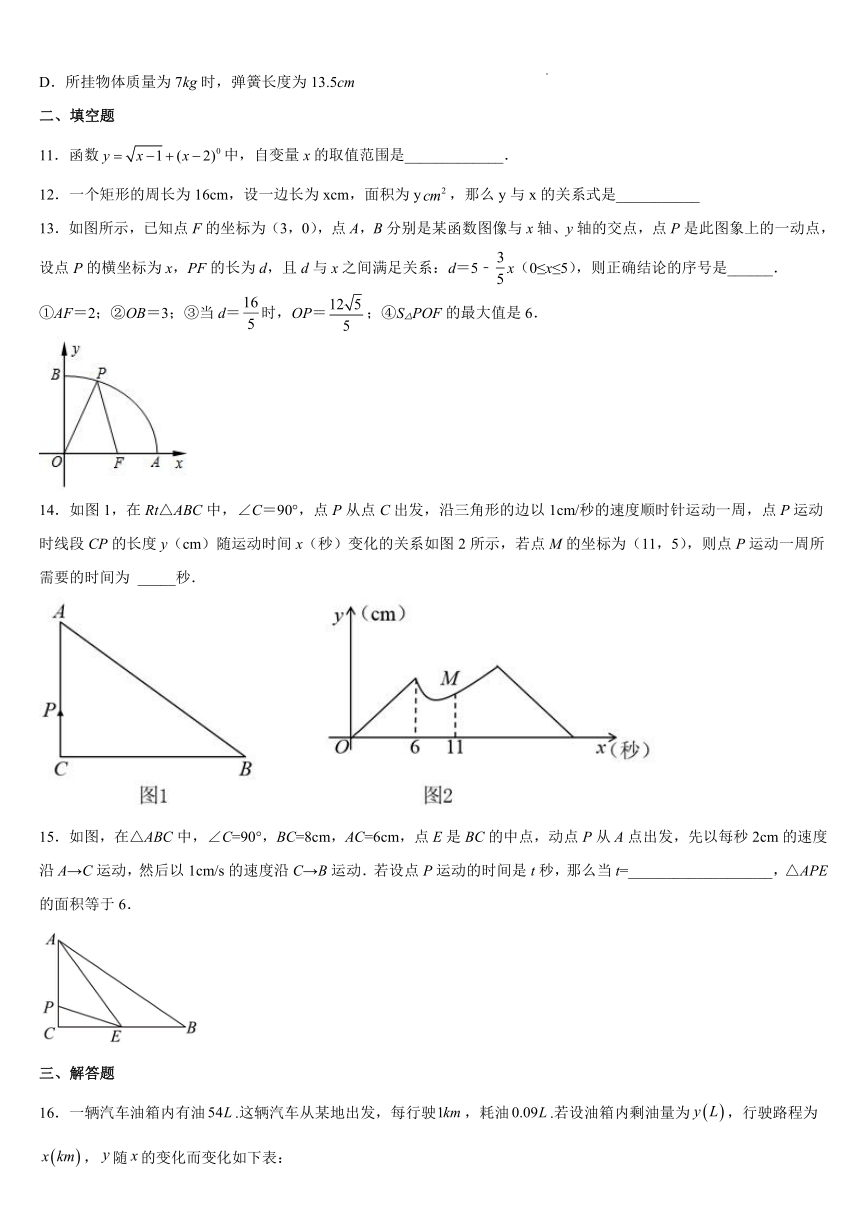
9.如图①,在矩形ABCD中,点M从点A出发以每秒1个单位长度的速度匀速运动到点B,点N沿A-D-C-B的顺序匀速运动,速度为每秒2个单位长度,当点M运动到点B时,M、N同时停止运动,设点M出发t秒时,△AMN的面积为S,如果S与t的函数关系如图②所示(其中0≤t≤2和6≤t≤8段为抛物线,2≤t≤6段为线段),那么下列说法不正确的是( )
A.当点M运动到点B时,点N也运动到点B B.矩形ABCD的周长是12
C.当2≤t≤6时,S=2t D.当t=7时,S=7
10.弹簧大家了解吗?弹簧挂上物体后会伸长。测得一弹簧的长度y(cm)与所挂的物体的重量x(kg)间有下面的关系:
x 0 1 2 3 4 5
y 10 10.5 11 11.5 12 12.5
下列说法不正确的是( )A.x与y都是变量,且x是自变量,y是因变量
B.物体质量每增加1kg,弹簧长度y增加0.5cm
C.y与x的关系表达式是y=0.5x
D.所挂物体质量为7kg时,弹簧长度为13.5cm
二、填空题
11.函数中,自变量x的取值范围是_____________.
12.一个矩形的周长为16cm,设一边长为xcm,面积为y,那么y与x的关系式是___________
13.如图所示,已知点F的坐标为(3,0),点A,B分别是某函数图像与x轴、y轴的交点,点P是此图象上的一动点,设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5﹣x(0≤x≤5),则正确结论的序号是______.
①AF=2;②OB=3;③当d=时,OP=;④S△POF的最大值是6.
14.如图1,在Rt△ABC中,∠C=90°,点P从点C出发,沿三角形的边以1cm/秒的速度顺时针运动一周,点P运动时线段CP的长度y(cm)随运动时间x(秒)变化的关系如图2所示,若点M的坐标为(11,5),则点P运动一周所需要的时间为 _____秒.
15.如图,在△ABC中,∠C=90°,BC=8cm,AC=6cm,点E是BC的中点,动点P从A点出发,先以每秒2cm的速度沿A→C运动,然后以1cm/s的速度沿C→B运动.若设点P运动的时间是t秒,那么当t=___________________,△APE的面积等于6.
三、解答题
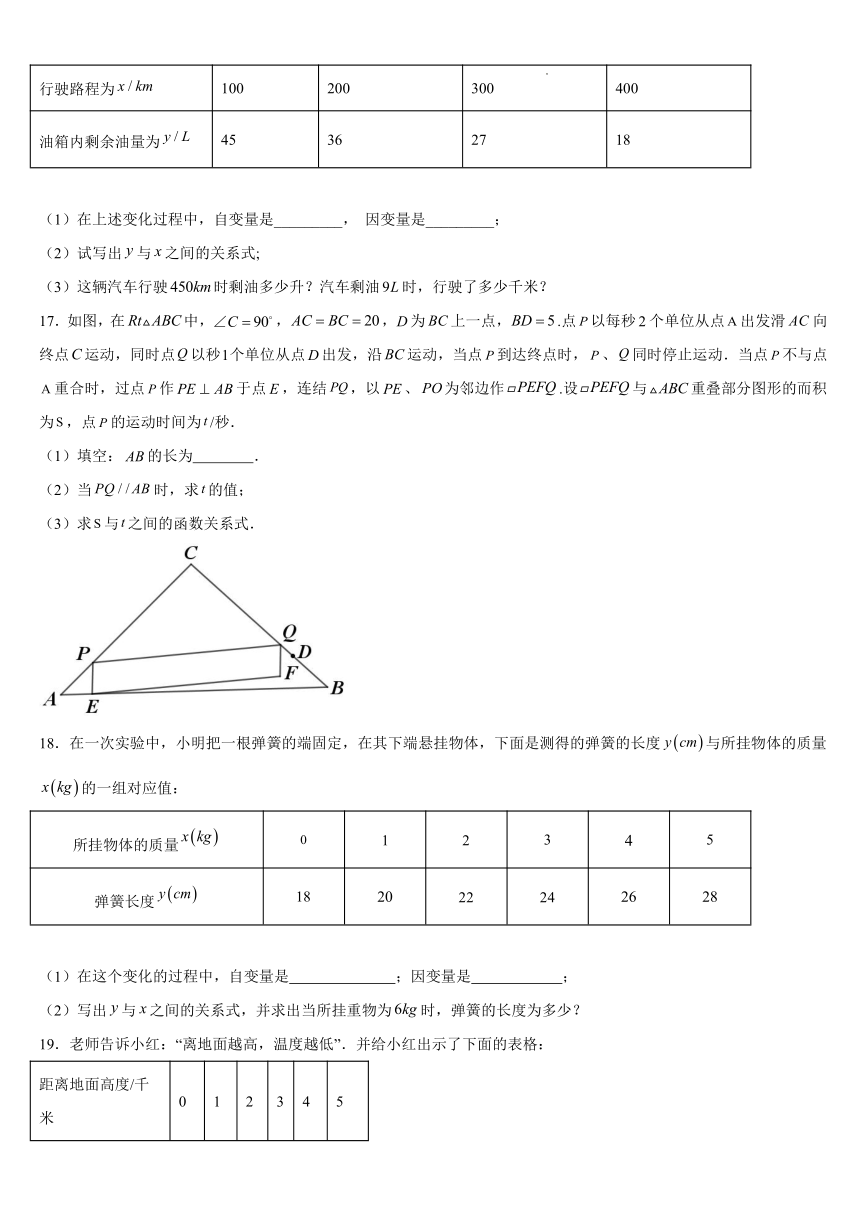
16.一辆汽车油箱内有油.这辆汽车从某地出发,每行驶,耗油.若设油箱内剩油量为,行驶路程为,随的变化而变化如下表:
行驶路程为 100 200 300 400
油箱内剩余油量为 45 36 27 18
(1)在上述变化过程中,自变量是_________, 因变量是_________;
(2)试写出与之间的关系式;
(3)这辆汽车行驶时剩油多少升?汽车剩油时,行驶了多少千米?
17.如图,在中,,,为上一点,.点以每秒个单位从点出发滑向终点运动,同时点以秒个单位从点出发,沿运动,当点到达终点时,、同时停止运动.当点不与点重合时,过点作于点,连结,以、为邻边作.设与重叠部分图形的而积为,点的运动时间为/秒.
(1)填空:的长为 .
(2)当时,求的值;
(3)求与之间的函数关系式.
18.在一次实验中,小明把一根弹簧的端固定,在其下端悬挂物体,下面是测得的弹簧的长度与所挂物体的质量的一组对应值:
所挂物体的质量
弹簧长度
(1)在这个变化的过程中,自变量是 ;因变量是 ;
(2)写出与之间的关系式,并求出当所挂重物为时,弹簧的长度为多少?
19.老师告诉小红:“离地面越高,温度越低”.并给小红出示了下面的表格:
距离地面高度/千米 0 1 2 3 4 5
温度/摄氏度 20 14 8 2 4 10
根据上表,老师还给小红出了下面几个问题,请你和小红一起来回答
(1)上表反映了哪两个变量之间的关系 哪个是自变量 哪个是因变量
(2)如果用h表示距离地面的高度,用t表示温度,请你用关于h的式子表示t;
(3)请你利用(2)的结论求:距离地面8.5千米的高空温度是多少
20.琳琳通过新闻了解到,近来意大利“新冠肺炎”疫情愈发严重,决定给意大利的网友Carlo邮寄一批防疫用品.已知琳琳家、药店、邮局在同一直线上,琳琳从家出发,跑步去药店买了酒精和口罩,又步行到邮局把物品寄出,然后再走回家.琳琳离家的距离y与时间x之间的关系如图所示,请根据图象解决下列问题:
(1)琳琳家离药店的距离为 km.
(2)琳琳邮寄物品用了 min.
(3)琳琳两段步行的速度分别是多少?
(4)图中点P的意义是 .
21.A、B两地相距60km,甲、乙两人从两地出发相向而行,甲先出发,图中l1,l2表示两人离A地的距离s(km)与时间t(h)的关系,请结合图象解答下列问题:
(1)表示乙离A地的距离与时间关系的图象是 (填“l1”或“l2”);甲的速度是 km/h,乙的速度是 km/h.
(2)甲出发多长时间两人相遇?
(3)甲出发多长时间后两人恰好相距5km?
22.甲骑车从A地到B地,乙骑车从B地到A地,甲的速度小于乙的速度,两人同时出发,沿同一条道路骑行,图中的折线表示两人之间的距离y(km)与甲的行驶时间x(h)之间的关系,根据图象回答下列问题:
(1)甲骑完全程用时 小时;甲的速度是 km/h;
(2)求甲、乙相遇的时间;
(3)求甲出发多长时间两人相距10千米.
23.小王上午8时自驾小汽车从家里出发,到“番茄农庄”游玩,小汽车离家的距离s(千米)与对应的时刻t(时)的关系可以用图中的折线表示,根据图像提供的有关信息,解答下列问题:
(1)“番茄农庄”离小王家________千米;
(2)小王在“番茄农庄”游玩了_______小时;
(3)在去“番茄农庄”的过程中,小汽车的平均速度是______千米/小时;
(4)小王回到家的时刻是______时_____分.
【参考答案】
1.D 2.B 3.B 4.B 5.B 6.D 7.D 8.B 9.B 10.C
11.x≥1且x≠2
12.y=-x2+8x
13.①④
14.
15.1.5或5或9
16.(1)行驶的路程,油箱内剩余油量;(2);(3).
17.(1);(2)t=5;(3).
18.(1)所挂物体的质量;弹簧的长度(2)y=2x+18,30cm.
19.(1)温度与距离地面高度;高度是自变量,温度是自变量;(2);(3)
20.(1)2.5
(2)20
(3)从药店步行到邮局的速度为km/min;从邮局步行回家的速度为(km/min)
(4)离家45min时,琳琳到达邮局,此时她离家的距离为1.5km
21.(1)l2,30,20;(2)甲出发1.4h后两人相遇;(3)甲出发1.3h或1.5h时后两人恰好相距5km
22.(1)3,10;(2);(3)或小时.
23.(1)90;
(2)4;
(3)45;
(4)16,15.
一、选择题
1.下列各曲线中,不表示y是x的函数的是( )
A. B. C. D.
2.已知一个等腰三角形的腰长为x,底边长为y,周长是10,则底边y关于腰长x之间的函数关系式及定义域为( )
A.y=10﹣2x(5<x<10) B.y=10﹣2x(2.5<x<5)
C.y=10﹣2x(0<x<5) D.y=10﹣2x(0<x<10)
3.函数y=中,自变量x的取值范围是( )
A.x≥-1 B.x≥-1且x≠3 C.x≠-1 D.x≠-1且x≠3
4.某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据
温度/℃ ﹣20 ﹣10 0 10 20 30
声速/m/s 318 324 330 336 342 348
下列说法错误的是( )A.这个问题中,空气温度和声速都是变量
B.空气温度每降低10℃,声速减少6m/s
C.当空气温度为20℃时,声音5s可以传播1710m
D.由数据可以推测,在一定范围内,空气温度越高,声速越快
5.将长为,宽为的长方形白纸,按如图所示的方法黏合起来,黏合的部分宽为.当黏合后的纸条总长度为,则需长方形白纸的数量为( )
A.18 B.19 C.20 D.21
6.《龟兔赛跑》是我们非常熟悉的故事.大意是乌龟和兔子赛跑,兔子开始就超过乌龟好远,兔子不耐烦了就在路边睡了一觉,乌龟一直往目的地奔跑,最终乌龟获得了胜利.下面能反映这个故事情节的图像是哪个?( )
A.B.C.D.
7.如图①,在中,,点是边的中点,点从的顶点出发,沿的路线以每秒1个单位长度的速度匀速运动到点,在运动过程中,线段的长度随时间变化的关系图象如图②所示,点是曲线部分的最低点,则的长为( )
A.3 B. C.12 D.
8.变量的一些对应值如下表:
… …
… …
根据表格中的数据规律,当时,的值是( )A. B. C. D.
9.如图①,在矩形ABCD中,点M从点A出发以每秒1个单位长度的速度匀速运动到点B,点N沿A-D-C-B的顺序匀速运动,速度为每秒2个单位长度,当点M运动到点B时,M、N同时停止运动,设点M出发t秒时,△AMN的面积为S,如果S与t的函数关系如图②所示(其中0≤t≤2和6≤t≤8段为抛物线,2≤t≤6段为线段),那么下列说法不正确的是( )
A.当点M运动到点B时,点N也运动到点B B.矩形ABCD的周长是12
C.当2≤t≤6时,S=2t D.当t=7时,S=7
10.弹簧大家了解吗?弹簧挂上物体后会伸长。测得一弹簧的长度y(cm)与所挂的物体的重量x(kg)间有下面的关系:
x 0 1 2 3 4 5
y 10 10.5 11 11.5 12 12.5
下列说法不正确的是( )A.x与y都是变量,且x是自变量,y是因变量
B.物体质量每增加1kg,弹簧长度y增加0.5cm
C.y与x的关系表达式是y=0.5x
D.所挂物体质量为7kg时,弹簧长度为13.5cm
二、填空题
11.函数中,自变量x的取值范围是_____________.
12.一个矩形的周长为16cm,设一边长为xcm,面积为y,那么y与x的关系式是___________
13.如图所示,已知点F的坐标为(3,0),点A,B分别是某函数图像与x轴、y轴的交点,点P是此图象上的一动点,设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5﹣x(0≤x≤5),则正确结论的序号是______.
①AF=2;②OB=3;③当d=时,OP=;④S△POF的最大值是6.
14.如图1,在Rt△ABC中,∠C=90°,点P从点C出发,沿三角形的边以1cm/秒的速度顺时针运动一周,点P运动时线段CP的长度y(cm)随运动时间x(秒)变化的关系如图2所示,若点M的坐标为(11,5),则点P运动一周所需要的时间为 _____秒.
15.如图,在△ABC中,∠C=90°,BC=8cm,AC=6cm,点E是BC的中点,动点P从A点出发,先以每秒2cm的速度沿A→C运动,然后以1cm/s的速度沿C→B运动.若设点P运动的时间是t秒,那么当t=___________________,△APE的面积等于6.
三、解答题
16.一辆汽车油箱内有油.这辆汽车从某地出发,每行驶,耗油.若设油箱内剩油量为,行驶路程为,随的变化而变化如下表:
行驶路程为 100 200 300 400
油箱内剩余油量为 45 36 27 18
(1)在上述变化过程中,自变量是_________, 因变量是_________;
(2)试写出与之间的关系式;
(3)这辆汽车行驶时剩油多少升?汽车剩油时,行驶了多少千米?
17.如图,在中,,,为上一点,.点以每秒个单位从点出发滑向终点运动,同时点以秒个单位从点出发,沿运动,当点到达终点时,、同时停止运动.当点不与点重合时,过点作于点,连结,以、为邻边作.设与重叠部分图形的而积为,点的运动时间为/秒.
(1)填空:的长为 .
(2)当时,求的值;
(3)求与之间的函数关系式.
18.在一次实验中,小明把一根弹簧的端固定,在其下端悬挂物体,下面是测得的弹簧的长度与所挂物体的质量的一组对应值:
所挂物体的质量
弹簧长度
(1)在这个变化的过程中,自变量是 ;因变量是 ;
(2)写出与之间的关系式,并求出当所挂重物为时,弹簧的长度为多少?
19.老师告诉小红:“离地面越高,温度越低”.并给小红出示了下面的表格:
距离地面高度/千米 0 1 2 3 4 5
温度/摄氏度 20 14 8 2 4 10
根据上表,老师还给小红出了下面几个问题,请你和小红一起来回答
(1)上表反映了哪两个变量之间的关系 哪个是自变量 哪个是因变量
(2)如果用h表示距离地面的高度,用t表示温度,请你用关于h的式子表示t;
(3)请你利用(2)的结论求:距离地面8.5千米的高空温度是多少
20.琳琳通过新闻了解到,近来意大利“新冠肺炎”疫情愈发严重,决定给意大利的网友Carlo邮寄一批防疫用品.已知琳琳家、药店、邮局在同一直线上,琳琳从家出发,跑步去药店买了酒精和口罩,又步行到邮局把物品寄出,然后再走回家.琳琳离家的距离y与时间x之间的关系如图所示,请根据图象解决下列问题:
(1)琳琳家离药店的距离为 km.
(2)琳琳邮寄物品用了 min.
(3)琳琳两段步行的速度分别是多少?
(4)图中点P的意义是 .
21.A、B两地相距60km,甲、乙两人从两地出发相向而行,甲先出发,图中l1,l2表示两人离A地的距离s(km)与时间t(h)的关系,请结合图象解答下列问题:
(1)表示乙离A地的距离与时间关系的图象是 (填“l1”或“l2”);甲的速度是 km/h,乙的速度是 km/h.
(2)甲出发多长时间两人相遇?
(3)甲出发多长时间后两人恰好相距5km?
22.甲骑车从A地到B地,乙骑车从B地到A地,甲的速度小于乙的速度,两人同时出发,沿同一条道路骑行,图中的折线表示两人之间的距离y(km)与甲的行驶时间x(h)之间的关系,根据图象回答下列问题:
(1)甲骑完全程用时 小时;甲的速度是 km/h;
(2)求甲、乙相遇的时间;
(3)求甲出发多长时间两人相距10千米.
23.小王上午8时自驾小汽车从家里出发,到“番茄农庄”游玩,小汽车离家的距离s(千米)与对应的时刻t(时)的关系可以用图中的折线表示,根据图像提供的有关信息,解答下列问题:
(1)“番茄农庄”离小王家________千米;
(2)小王在“番茄农庄”游玩了_______小时;
(3)在去“番茄农庄”的过程中,小汽车的平均速度是______千米/小时;
(4)小王回到家的时刻是______时_____分.
【参考答案】
1.D 2.B 3.B 4.B 5.B 6.D 7.D 8.B 9.B 10.C
11.x≥1且x≠2
12.y=-x2+8x
13.①④
14.
15.1.5或5或9
16.(1)行驶的路程,油箱内剩余油量;(2);(3).
17.(1);(2)t=5;(3).
18.(1)所挂物体的质量;弹簧的长度(2)y=2x+18,30cm.
19.(1)温度与距离地面高度;高度是自变量,温度是自变量;(2);(3)
20.(1)2.5
(2)20
(3)从药店步行到邮局的速度为km/min;从邮局步行回家的速度为(km/min)
(4)离家45min时,琳琳到达邮局,此时她离家的距离为1.5km
21.(1)l2,30,20;(2)甲出发1.4h后两人相遇;(3)甲出发1.3h或1.5h时后两人恰好相距5km
22.(1)3,10;(2);(3)或小时.
23.(1)90;
(2)4;
(3)45;
(4)16,15.
