2021-2022学年冀教版九年级数学下册第三十一章随机事件的概率单元检测(Word版含答案)
文档属性
| 名称 | 2021-2022学年冀教版九年级数学下册第三十一章随机事件的概率单元检测(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 354.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-20 18:41:05 | ||
图片预览




文档简介
第三十一章 随机事件的概率单元检测
一、单选题
1.下列事件为必然事件的是( )
A.打开电视机,正在播放新闻
B.掷一枚质地均匀的硬币,正面朝上
C.经过有交通信号灯的路口,遇到绿灯
D.任意画一个三角形,其内角和是180°
2.下列说法不正确的是( )
A.在装有红球、白球的盒子中摸出绿球是不可能事件
B.抛掷一枚硬币,落地时正面朝上是随机事件
C.13个人中至少有两个人出生的月份相同是必然事件
D.明天会下雨是必然事件
3.在正面完全相同、反面印有下列四个图形的纸片中,任抽一张,则抽到的纸片上的图形恰好是中心对称图形的概率为( )
A. B. C. D.1
4.“某彩票的中奖率是1%”,下列对这句话的理解,说法一定正确的是( )
A.买1张彩票肯定不会中奖 B.买100张彩票肯定会中1张奖
C.买1张彩票也可能会中奖 D.一次买下所有彩票的一半,肯定1%张彩票中奖
5.如图,正方形ABCD内接于⊙O,⊙O的直径为,若在这个圆面上随意抛一粒豆子,则豆子落在正方形ABCD内的概率是( )
A. B. C. D.1
6.嘉淇在一次实验中,把四张扑克牌洗匀后,背面向上放在桌面上,并从中随机抽取一张,记录牌面上的数字出现的频率,并制成折线统计图,则符合这个结果的实验可能是( )
A.牌面数字是2的倍数 B.牌面数字是3的倍数
C.牌面数字是4的倍数 D.牌面数字是5的倍数
7.从A,B,C三张卡片中任取两张,取到A,B的概率是( )
A. B. C. D.
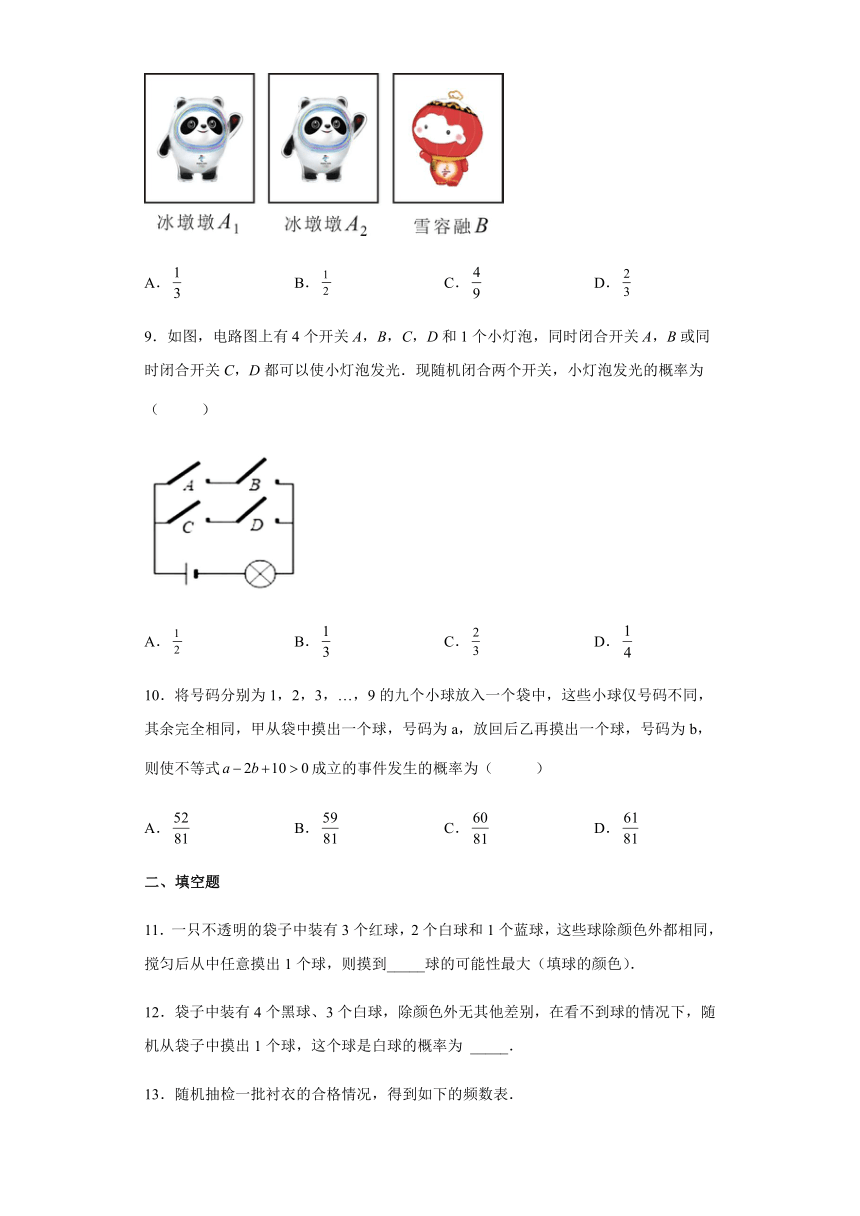
8.2022年冬奥会古祥物为“冰墩墩”,冬残奥会吉祥物为“雪容融”.如图,现有三张正面明有吉祥物的不透明卡片,卡片除正两图案不同外,其余均相同,其中两张正面印有冰墩墩图案,一张正面印有雪容融图案,将三张卡片正面向下洗匀,从中随机仙取两张卡片,则抽出的两张都是冰墩墩卡片的概率事( )
A. B. C. D.
9.如图,电路图上有4个开关A,B,C,D和1个小灯泡,同时闭合开关A,B或同时闭合开关C,D都可以使小灯泡发光.现随机闭合两个开关,小灯泡发光的概率为( )
A. B. C. D.
10.将号码分别为1,2,3,…,9的九个小球放入一个袋中,这些小球仅号码不同,其余完全相同,甲从袋中摸出一个球,号码为a,放回后乙再摸出一个球,号码为b,则使不等式成立的事件发生的概率为( )
A. B. C. D.
二、填空题
11.一只不透明的袋子中装有3个红球,2个白球和1个蓝球,这些球除颜色外都相同,搅匀后从中任意摸出1个球,则摸到_____球的可能性最大(填球的颜色).
12.袋子中装有4个黑球、3个白球,除颜色外无其他差别,在看不到球的情况下,随机从袋子中摸出1个球,这个球是白球的概率为 _____.
13.随机抽检一批衬衣的合格情况,得到如下的频数表.
抽取件数(件) 100 150 200 500 800 1000
合格频数 900 141 189 474 760 950
合格频率 0.90 0.94 0.945 0.948 0.95 0.95
则出售这批衬衣2000件,估计次品大约有______件.
14.在一个不透明的盒子里有四个分别写有,,1,2数字的小球,它们除数字不同外其余全部相同,现从盒子里随机取出一个小球,将小球上的数字记为m,然后在剩下的小球中随机再取出一个,将小球上的数字记为n,则的值为负数的概率是____________
15.如图,小颖在围棋盘上两个格子的格点上任意摆放黑、白两个棋子,且两个棋子不在同一条网格线上,其中,恰好摆放成如图所示位置的概率是______.
三、解答题
16.指出下列事件中,哪些是必然事件,哪些是不可能事件.
①两条平行线被第三条直线所截,同位角相等;
②367人中至少有2人的生日相同;
③没有水分,种子也会发芽;
④某运动员百米赛跑的成绩是;
⑤同种电荷相互排斥;
⑥通常情况下,高铁比普通列车快;
⑦用长度分别为3 cm,5 cm,8 cm的三条线段能围成一个三角形.
17.在一个不透明的盒子里装着只有颜色不同的黑、白两种球共5个,小明做摸球实验,他将盒子里面的球搅匀后从中随机摸出一球记下颜色,再把它放回盒子,不断重复上述过程实验n次,下表是小明“摸到白球”的频数、频率统计表.
摸球实验次数n 10 100 150 200 500 …
摸到白球的频数m 2 22 31 39 101 …
摸到白球的频率p 0.200 0.220 0.207 0.195 0.202 …
(1)观察上表,可以推测,摸一次摸到白球的概率为______.
(2)请你估计盒子里白球个数.
(3)若往盒子中同时放入x个白球和y个黑球,从盒子中随机取出一个白球的概率是0.25,求y与x之间的函数关系式.
18.临近考试,某学校为考生提供下列减压方式:
A.交流谈心;
B.有氧运动;
C.欣赏音乐;
D.安静休息.
考生可从中选择一种方式进行减压.
(1)随机抽查一名考生,其选择“欣赏音乐”的概率是 ;
(2)随机抽查两名考生,其中至少有一人选择“有氧运动”的概率为多少?请用画树状图或列表的方法加以说明.
19.如图,现有A、B两转盘分别被均分4等份和3等分,A转盘分别标有2、4、6、8这四个数字,B转盘分别标有1、3、5.转动转盘,当转盘停止时,指针指向的数字即为转出的数字,求:
(1)转动转盘A,转到数字1是_______;转到数字6是________;(从“随机事件”、“必然事件”、“不可能事件”选一个填入);转出的数字大于4的概率是_______.
(2)现有一张写有7的卡片,分别随机转动A、B转盘,转盘停止分别记下转出的数字,与卡片上的数字分别作为三条线段的长度.请用画树状图或列表的方法,求出这三条线段能构成三角形的概率.
试卷第1页,共3页
答案
1.D
2.D
3.B
4.C
5.B
6.B
7.C
8.A
9.B
10.D
11.红
12.
13.100
14.
15.
16.解:①两条平行线被第三条直线所截,同位角相等,是必然事件;
②367人中至少有2人的生日相同,是必然事件;
③没有水分,种子也会发芽,是不可能事件;
④某运动员百米赛跑的成绩是,是不可能事件,;
⑤同种电荷相互排斥,是必然事件;
⑥通常情况下,高铁比普通列车快,是必然事件;
⑦用长度分别为,,的三条线段能围成一个三角形,是不可能事件;
∴必然事件:①②⑤⑥;
不可能事件:③④⑦.
17.(1) 观察表格发现摸到白球的频率在0.2左右波动,
摸到白球的频率为0.2
(2)设盒子里白球有m个,根据题意得,
解得m=1.
答:盒子里白球有1个.
(3)解:由题意得:.
化简整理得:.
∴y与x之间的函数关系式为:.(x为正整数)
18.(1)解:随机抽查一名考生,其选择“欣赏音乐”的概率是;
故答案为:;
(2)解:画树状图如下:
共有16种等可能的结果,至少有一人选择“有氧运动”的结果有7种,
则至少有一人选择“有氧运动”的概率是.
19.(1)解:转盘A中没有数字1,故转到数字1是不可能事件,
转盘A中有数字6但不只有数字6,故转到数字6是随机事件,
转盘A中被分为4等分,共有4个数字,故转到每个数字的概率相等,是等可能事件,大于4的数字有两个,故转出数字大于4的概率是,
故答案为:不可能事件;随机事件;.
(2)树状图如下图所示:
,
由树状图可知一共有12种情况,其中能组成三角形的情况有5种,
所以这三条线段能构成三角形的概率为.答案第1页,共2页
一、单选题
1.下列事件为必然事件的是( )
A.打开电视机,正在播放新闻
B.掷一枚质地均匀的硬币,正面朝上
C.经过有交通信号灯的路口,遇到绿灯
D.任意画一个三角形,其内角和是180°
2.下列说法不正确的是( )
A.在装有红球、白球的盒子中摸出绿球是不可能事件
B.抛掷一枚硬币,落地时正面朝上是随机事件
C.13个人中至少有两个人出生的月份相同是必然事件
D.明天会下雨是必然事件
3.在正面完全相同、反面印有下列四个图形的纸片中,任抽一张,则抽到的纸片上的图形恰好是中心对称图形的概率为( )
A. B. C. D.1
4.“某彩票的中奖率是1%”,下列对这句话的理解,说法一定正确的是( )
A.买1张彩票肯定不会中奖 B.买100张彩票肯定会中1张奖
C.买1张彩票也可能会中奖 D.一次买下所有彩票的一半,肯定1%张彩票中奖
5.如图,正方形ABCD内接于⊙O,⊙O的直径为,若在这个圆面上随意抛一粒豆子,则豆子落在正方形ABCD内的概率是( )
A. B. C. D.1
6.嘉淇在一次实验中,把四张扑克牌洗匀后,背面向上放在桌面上,并从中随机抽取一张,记录牌面上的数字出现的频率,并制成折线统计图,则符合这个结果的实验可能是( )
A.牌面数字是2的倍数 B.牌面数字是3的倍数
C.牌面数字是4的倍数 D.牌面数字是5的倍数
7.从A,B,C三张卡片中任取两张,取到A,B的概率是( )
A. B. C. D.
8.2022年冬奥会古祥物为“冰墩墩”,冬残奥会吉祥物为“雪容融”.如图,现有三张正面明有吉祥物的不透明卡片,卡片除正两图案不同外,其余均相同,其中两张正面印有冰墩墩图案,一张正面印有雪容融图案,将三张卡片正面向下洗匀,从中随机仙取两张卡片,则抽出的两张都是冰墩墩卡片的概率事( )
A. B. C. D.
9.如图,电路图上有4个开关A,B,C,D和1个小灯泡,同时闭合开关A,B或同时闭合开关C,D都可以使小灯泡发光.现随机闭合两个开关,小灯泡发光的概率为( )
A. B. C. D.
10.将号码分别为1,2,3,…,9的九个小球放入一个袋中,这些小球仅号码不同,其余完全相同,甲从袋中摸出一个球,号码为a,放回后乙再摸出一个球,号码为b,则使不等式成立的事件发生的概率为( )
A. B. C. D.
二、填空题
11.一只不透明的袋子中装有3个红球,2个白球和1个蓝球,这些球除颜色外都相同,搅匀后从中任意摸出1个球,则摸到_____球的可能性最大(填球的颜色).
12.袋子中装有4个黑球、3个白球,除颜色外无其他差别,在看不到球的情况下,随机从袋子中摸出1个球,这个球是白球的概率为 _____.
13.随机抽检一批衬衣的合格情况,得到如下的频数表.
抽取件数(件) 100 150 200 500 800 1000
合格频数 900 141 189 474 760 950
合格频率 0.90 0.94 0.945 0.948 0.95 0.95
则出售这批衬衣2000件,估计次品大约有______件.
14.在一个不透明的盒子里有四个分别写有,,1,2数字的小球,它们除数字不同外其余全部相同,现从盒子里随机取出一个小球,将小球上的数字记为m,然后在剩下的小球中随机再取出一个,将小球上的数字记为n,则的值为负数的概率是____________
15.如图,小颖在围棋盘上两个格子的格点上任意摆放黑、白两个棋子,且两个棋子不在同一条网格线上,其中,恰好摆放成如图所示位置的概率是______.
三、解答题
16.指出下列事件中,哪些是必然事件,哪些是不可能事件.
①两条平行线被第三条直线所截,同位角相等;
②367人中至少有2人的生日相同;
③没有水分,种子也会发芽;
④某运动员百米赛跑的成绩是;
⑤同种电荷相互排斥;
⑥通常情况下,高铁比普通列车快;
⑦用长度分别为3 cm,5 cm,8 cm的三条线段能围成一个三角形.
17.在一个不透明的盒子里装着只有颜色不同的黑、白两种球共5个,小明做摸球实验,他将盒子里面的球搅匀后从中随机摸出一球记下颜色,再把它放回盒子,不断重复上述过程实验n次,下表是小明“摸到白球”的频数、频率统计表.
摸球实验次数n 10 100 150 200 500 …
摸到白球的频数m 2 22 31 39 101 …
摸到白球的频率p 0.200 0.220 0.207 0.195 0.202 …
(1)观察上表,可以推测,摸一次摸到白球的概率为______.
(2)请你估计盒子里白球个数.
(3)若往盒子中同时放入x个白球和y个黑球,从盒子中随机取出一个白球的概率是0.25,求y与x之间的函数关系式.
18.临近考试,某学校为考生提供下列减压方式:
A.交流谈心;
B.有氧运动;
C.欣赏音乐;
D.安静休息.
考生可从中选择一种方式进行减压.
(1)随机抽查一名考生,其选择“欣赏音乐”的概率是 ;
(2)随机抽查两名考生,其中至少有一人选择“有氧运动”的概率为多少?请用画树状图或列表的方法加以说明.
19.如图,现有A、B两转盘分别被均分4等份和3等分,A转盘分别标有2、4、6、8这四个数字,B转盘分别标有1、3、5.转动转盘,当转盘停止时,指针指向的数字即为转出的数字,求:
(1)转动转盘A,转到数字1是_______;转到数字6是________;(从“随机事件”、“必然事件”、“不可能事件”选一个填入);转出的数字大于4的概率是_______.
(2)现有一张写有7的卡片,分别随机转动A、B转盘,转盘停止分别记下转出的数字,与卡片上的数字分别作为三条线段的长度.请用画树状图或列表的方法,求出这三条线段能构成三角形的概率.
试卷第1页,共3页
答案
1.D
2.D
3.B
4.C
5.B
6.B
7.C
8.A
9.B
10.D
11.红
12.
13.100
14.
15.
16.解:①两条平行线被第三条直线所截,同位角相等,是必然事件;
②367人中至少有2人的生日相同,是必然事件;
③没有水分,种子也会发芽,是不可能事件;
④某运动员百米赛跑的成绩是,是不可能事件,;
⑤同种电荷相互排斥,是必然事件;
⑥通常情况下,高铁比普通列车快,是必然事件;
⑦用长度分别为,,的三条线段能围成一个三角形,是不可能事件;
∴必然事件:①②⑤⑥;
不可能事件:③④⑦.
17.(1) 观察表格发现摸到白球的频率在0.2左右波动,
摸到白球的频率为0.2
(2)设盒子里白球有m个,根据题意得,
解得m=1.
答:盒子里白球有1个.
(3)解:由题意得:.
化简整理得:.
∴y与x之间的函数关系式为:.(x为正整数)
18.(1)解:随机抽查一名考生,其选择“欣赏音乐”的概率是;
故答案为:;
(2)解:画树状图如下:
共有16种等可能的结果,至少有一人选择“有氧运动”的结果有7种,
则至少有一人选择“有氧运动”的概率是.
19.(1)解:转盘A中没有数字1,故转到数字1是不可能事件,
转盘A中有数字6但不只有数字6,故转到数字6是随机事件,
转盘A中被分为4等分,共有4个数字,故转到每个数字的概率相等,是等可能事件,大于4的数字有两个,故转出数字大于4的概率是,
故答案为:不可能事件;随机事件;.
(2)树状图如下图所示:
,
由树状图可知一共有12种情况,其中能组成三角形的情况有5种,
所以这三条线段能构成三角形的概率为.答案第1页,共2页
