2021-2022学年苏科版七年级数学下册第7章平面图形的认识(二)单元练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版七年级数学下册第7章平面图形的认识(二)单元练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 138.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-20 18:41:10 | ||
图片预览

文档简介
2021-2022学年苏科版七年级数学下册《第7章平面图形的认识(二)》
单元练习题(附答案)
一.选择题(共8小题,满分40分)
1.下列图形中有稳定性的是( )
A.正方形 B.长方形 C.直角三角形 D.平行四边形
2. 一个多边形有20条对角线,则边数为( )
A.8 B.9 C.11 D.12
3 一个正多边形的每个内角的度数都等于相邻外角的2倍,则该正多边形的边数是( )
A.3 B.4 C.6 D.12
4.下列图形中,∠1与∠2是同位角的是( )
A. B.
C. D.
5.如图,已知AB,CD是两条相交线段,连结AD,CB,分别作∠DAB和∠BCD的平分线相交于点P,若∠D=50°,∠B=40°,则∠P的度数为( )
A.50° B.45° C.40° D.30°
6.如图,若AB∥DE,∠B=130°,∠D=35°,则∠C的度数为( )
A.80° B.85° C.90° D.95°
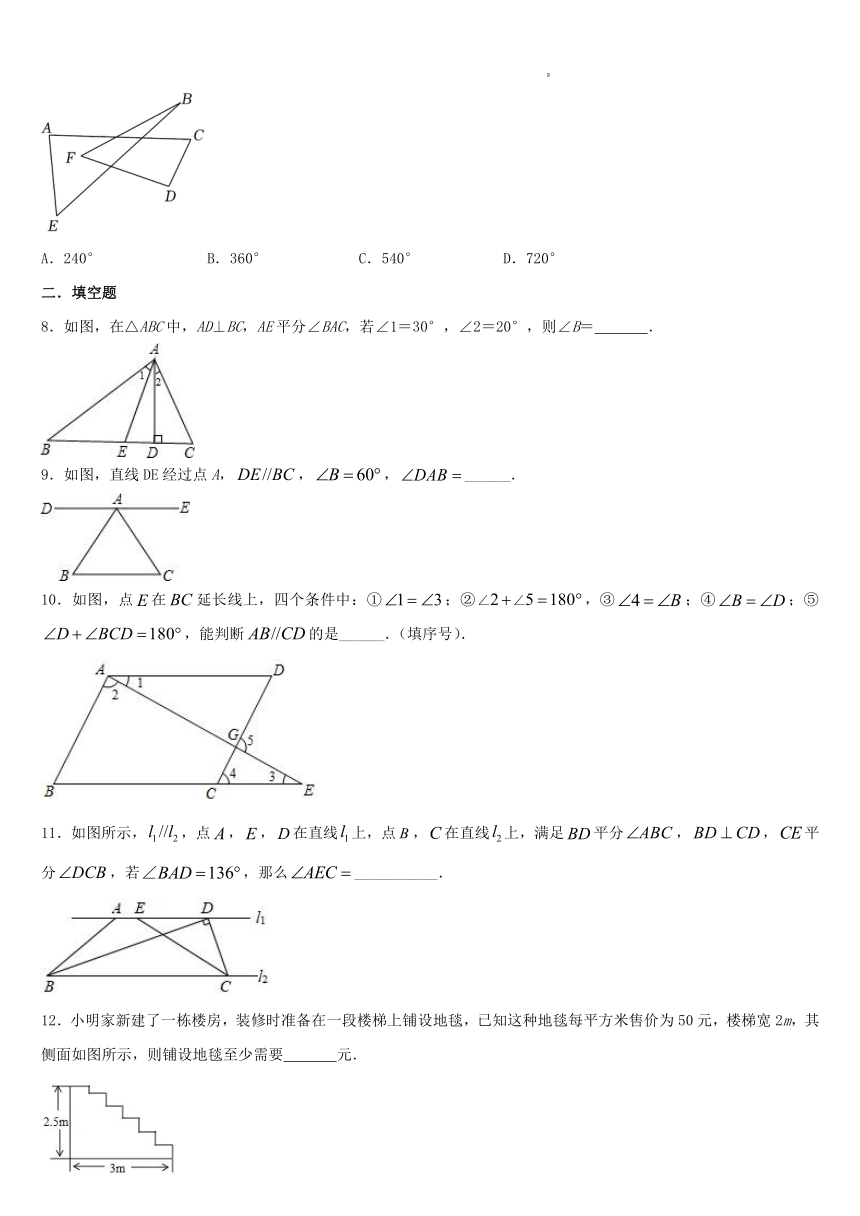
7.如图,∠A+∠B+∠C+∠D+∠E+∠F的值是( )
A.240° B.360° C.540° D.720°
二.填空题
8.如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=30°,∠2=20°,则∠B= .
9.如图,直线DE经过点A,,,______.
10.如图,点在延长线上,四个条件中:①;②,③;④;⑤,能判断的是______.(填序号).
11.如图所示,,点,,在直线上,点,在直线上,满足平分,,平分,若,那么___________.
12.小明家新建了一栋楼房,装修时准备在一段楼梯上铺设地毯,已知这种地毯每平方米售价为50元,楼梯宽2m,其侧面如图所示,则铺设地毯至少需要 元.
三.解答题
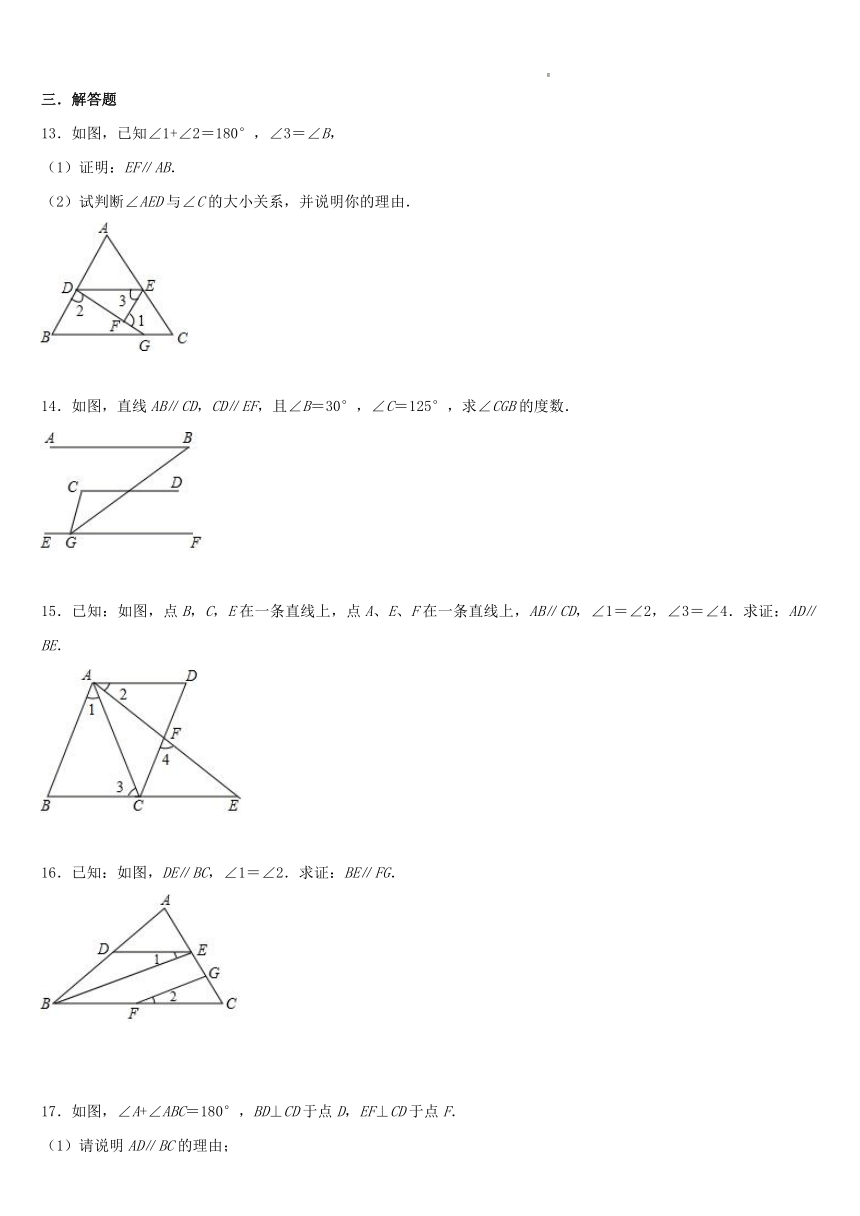
13.如图,已知∠1+∠2=180°,∠3=∠B,
(1)证明:EF∥AB.
(2)试判断∠AED与∠C的大小关系,并说明你的理由.
14.如图,直线AB∥CD,CD∥EF,且∠B=30°,∠C=125°,求∠CGB的度数.
15.已知:如图,点B,C,E在一条直线上,点A、E、F在一条直线上,AB∥CD,∠1=∠2,∠3=∠4.求证:AD∥BE.
16.已知:如图,DE∥BC,∠1=∠2.求证:BE∥FG.
17.如图,∠A+∠ABC=180°,BD⊥CD于点D,EF⊥CD于点F.
(1)请说明AD∥BC的理由;
(2)若∠ADB=45°,求∠FEC的度数.
18.如图,已知BC∥GE,∠AFG=∠1=50°.
(1)求证:AF∥DE;
(2)若AQ平分∠FAC,交BC于点Q,且∠Q=15°,求∠ACQ的度数.
参考答案
1.C
2.A
3.A
4.D
5.B
6.B
7.B
8.50°.
9(2)(5)
10.60°
11.②③
12.550.
13.解:(1)∵∠1+∠DFE=180°(平角定义),∠1+∠2=180°(已知),
∴∠2=∠DFE,
∴EF∥AB(内错角相等,两直线平行);
(2)∠AED与∠C相等.
∵EF∥AB,
∴∠3=∠ADE(两直线平行,内错角相等),
∵∠3=∠B(已知),
∴∠B=∠ADE(等量代换),
∴DE∥BC(同位角相等,两直线平行),
∴∠AED=∠C(两直线平行,同位角相等).
14.解:∵AB∥CD,CD∥EF,
∴AB∥CD∥EF,
∵∠B=30°,∠C=125°,
∴∠BGF=∠B=30°,∠C+∠CGF=180°,
∴∠CGF=55°,
∴∠CGB=∠CGF﹣∠BGF=25°.
15.证明:∵AB∥CD,
∴∠1=∠ACD,
∵∠1=∠2,
∴∠2=∠ACD,
∴∠2+∠CAE=∠ACD+∠CAE,
∴∠DAC=∠4,
∵∠3=∠4,
∴∠DAC=∠3,
∴AD∥BE.
16.证明:∵DE∥BC,
∴∠1=∠CBE.
∵∠1=∠2,
∴∠CBE=∠2,
∴BE∥FG.
17.解:如图所示:
(1)AD∥BC的理由如下:
∵∠A+∠ABC=180°,
∴AD∥BC(同旁内角互补,两直线平行);
(2)∵BD⊥CD,
∴∠BDC=90°,
∵AD∥BC,
∴∠ADB=∠DBC,
又∵∠ADB=45°,
∴∠DBC=45°,
又∵BD⊥CD.EF⊥CD,
∴BD∥EF,
∴∠DBC=∠FEC,
∴∠FEC=45°.
18(1)证明:∵BC∥GE,
∴∠E=∠1=50°,
∵∠AFG=∠1=50°,
∴∠E=∠AFG=50°,
∴AF∥DE;
(2)解:∵∠1=50°,∠Q=15°,
∴∠AHD=65°,
∵AF∥DE,
∴∠FAQ=∠AHD=65°,
∵AQ平分∠FAC,
∴∠CAQ=∠FAQ=65°,
∴∠ACQ=180°﹣∠CAQ﹣∠Q=180°﹣65°﹣15°=100°.
单元练习题(附答案)
一.选择题(共8小题,满分40分)
1.下列图形中有稳定性的是( )
A.正方形 B.长方形 C.直角三角形 D.平行四边形
2. 一个多边形有20条对角线,则边数为( )
A.8 B.9 C.11 D.12
3 一个正多边形的每个内角的度数都等于相邻外角的2倍,则该正多边形的边数是( )
A.3 B.4 C.6 D.12
4.下列图形中,∠1与∠2是同位角的是( )
A. B.
C. D.
5.如图,已知AB,CD是两条相交线段,连结AD,CB,分别作∠DAB和∠BCD的平分线相交于点P,若∠D=50°,∠B=40°,则∠P的度数为( )
A.50° B.45° C.40° D.30°
6.如图,若AB∥DE,∠B=130°,∠D=35°,则∠C的度数为( )
A.80° B.85° C.90° D.95°
7.如图,∠A+∠B+∠C+∠D+∠E+∠F的值是( )
A.240° B.360° C.540° D.720°
二.填空题
8.如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=30°,∠2=20°,则∠B= .
9.如图,直线DE经过点A,,,______.
10.如图,点在延长线上,四个条件中:①;②,③;④;⑤,能判断的是______.(填序号).
11.如图所示,,点,,在直线上,点,在直线上,满足平分,,平分,若,那么___________.
12.小明家新建了一栋楼房,装修时准备在一段楼梯上铺设地毯,已知这种地毯每平方米售价为50元,楼梯宽2m,其侧面如图所示,则铺设地毯至少需要 元.
三.解答题
13.如图,已知∠1+∠2=180°,∠3=∠B,
(1)证明:EF∥AB.
(2)试判断∠AED与∠C的大小关系,并说明你的理由.
14.如图,直线AB∥CD,CD∥EF,且∠B=30°,∠C=125°,求∠CGB的度数.
15.已知:如图,点B,C,E在一条直线上,点A、E、F在一条直线上,AB∥CD,∠1=∠2,∠3=∠4.求证:AD∥BE.
16.已知:如图,DE∥BC,∠1=∠2.求证:BE∥FG.
17.如图,∠A+∠ABC=180°,BD⊥CD于点D,EF⊥CD于点F.
(1)请说明AD∥BC的理由;
(2)若∠ADB=45°,求∠FEC的度数.
18.如图,已知BC∥GE,∠AFG=∠1=50°.
(1)求证:AF∥DE;
(2)若AQ平分∠FAC,交BC于点Q,且∠Q=15°,求∠ACQ的度数.
参考答案
1.C
2.A
3.A
4.D
5.B
6.B
7.B
8.50°.
9(2)(5)
10.60°
11.②③
12.550.
13.解:(1)∵∠1+∠DFE=180°(平角定义),∠1+∠2=180°(已知),
∴∠2=∠DFE,
∴EF∥AB(内错角相等,两直线平行);
(2)∠AED与∠C相等.
∵EF∥AB,
∴∠3=∠ADE(两直线平行,内错角相等),
∵∠3=∠B(已知),
∴∠B=∠ADE(等量代换),
∴DE∥BC(同位角相等,两直线平行),
∴∠AED=∠C(两直线平行,同位角相等).
14.解:∵AB∥CD,CD∥EF,
∴AB∥CD∥EF,
∵∠B=30°,∠C=125°,
∴∠BGF=∠B=30°,∠C+∠CGF=180°,
∴∠CGF=55°,
∴∠CGB=∠CGF﹣∠BGF=25°.
15.证明:∵AB∥CD,
∴∠1=∠ACD,
∵∠1=∠2,
∴∠2=∠ACD,
∴∠2+∠CAE=∠ACD+∠CAE,
∴∠DAC=∠4,
∵∠3=∠4,
∴∠DAC=∠3,
∴AD∥BE.
16.证明:∵DE∥BC,
∴∠1=∠CBE.
∵∠1=∠2,
∴∠CBE=∠2,
∴BE∥FG.
17.解:如图所示:
(1)AD∥BC的理由如下:
∵∠A+∠ABC=180°,
∴AD∥BC(同旁内角互补,两直线平行);
(2)∵BD⊥CD,
∴∠BDC=90°,
∵AD∥BC,
∴∠ADB=∠DBC,
又∵∠ADB=45°,
∴∠DBC=45°,
又∵BD⊥CD.EF⊥CD,
∴BD∥EF,
∴∠DBC=∠FEC,
∴∠FEC=45°.
18(1)证明:∵BC∥GE,
∴∠E=∠1=50°,
∵∠AFG=∠1=50°,
∴∠E=∠AFG=50°,
∴AF∥DE;
(2)解:∵∠1=50°,∠Q=15°,
∴∠AHD=65°,
∵AF∥DE,
∴∠FAQ=∠AHD=65°,
∵AQ平分∠FAC,
∴∠CAQ=∠FAQ=65°,
∴∠ACQ=180°﹣∠CAQ﹣∠Q=180°﹣65°﹣15°=100°.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
