2021—2022学年人教版八年级数学下册19.1.2函数的图像课后练习(Word版含答案)
文档属性
| 名称 | 2021—2022学年人教版八年级数学下册19.1.2函数的图像课后练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 327.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-20 00:00:00 | ||
图片预览


文档简介
2021——2022学年度人教版八年级数学下册 第十九章 一次函数
19.1.2 函数的图像 课后练习
一、选择题
1.函数的图象上的点一定在第( )象限
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.在平面直角坐标系中,下列函数的图象经过点的是( )
A. B. C. D.
3.柿子熟了,从树上落下来,下面的哪一幅图可以大致刻画出柿子下落过程中(即落地前)的速度变化情况( )
A. B. C. D.
4.我们要节约用水,平时要关好水龙头.没有关好水龙头,每滴水约0.05毫升,每分钟滴60滴.如果小明忘记关水龙头,则x分钟后,小明浪费的水y(毫升)与时间x(分钟)之间的函数关系是( )
A.y=60x B.y=3x C.y=0.05x D.y=0.05x+60
5.变量x,y的一些对应值如表:
x … ﹣2 ﹣1 0 1 2 3 …
y … 9 2 1 0 ﹣7 ﹣26 …
根据表格中的数据规律,当x=﹣5时,y的值是( )A.76 B.﹣74 C.126 D.﹣124
6.甲、乙两辆汽车在同一条路上匀速行驶,图①和图②表示汽车速度与时间的关系,图③和图④表示汽车路程与时间的关系,小明对4个图中汽车运动的情况进行了描述,其中正确的是( )
A.图①,乙的速度是甲的3倍,相同时间甲乙的路程相等
B.图②,乙的速度是甲的2倍,相同时间乙的路程是甲的一半
C.图③,乙的速度是甲的2倍,相同时间乙的路程是甲的一半
D.图④,乙的速度是甲的2倍,相同时间乙的路程是甲的2倍
7.如图是甲、乙两个动点在某时段速度随时间变化的图象,下列结论错误的是( )
A.乙点前4秒是匀速运动,4秒后速度不断增加 B.甲点比乙点早4秒将速度提升到32cm/s
C.在4至8秒内甲的速度都大于乙的速度 D.甲、乙两点到第3秒时运动的路程相等
8.甲、乙两人同时各接受了600个零件的加工任务,甲比乙每分钟加工的数量多,两人同时开始加工,加工过程中甲因故障停止一会后又继续按原速加工,直到他们完成任务.甲比乙多加工的零件数量(个)与加工时间(分)之间的函数关系如图所示,点的横坐标为12,点的坐标为,点的横坐标为128,则下列说法中不正确的是( )
A.甲每分钟加工的零件数量是5个 B.在60分钟时,甲比乙多加工了120个零件
C.点的横坐标是200 D.的最大值是216
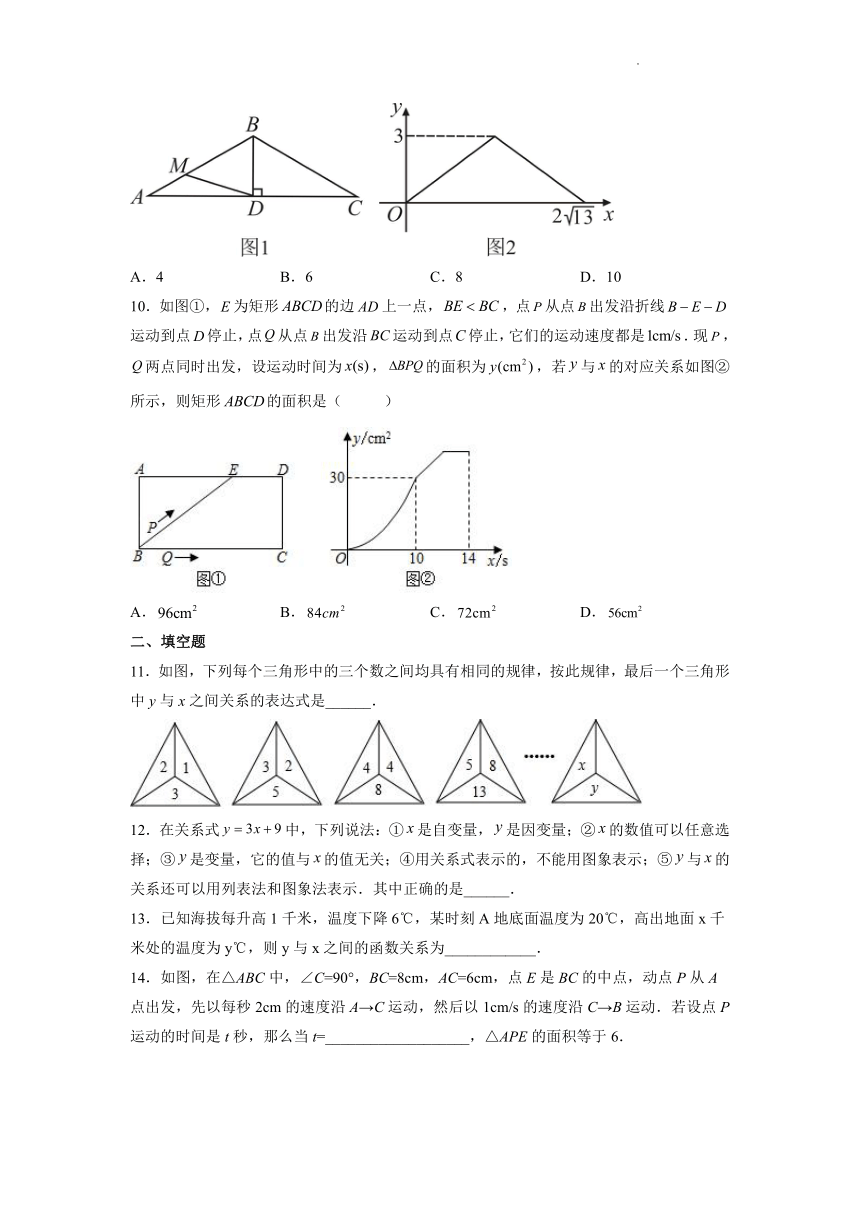
9.如图1,在中,,于点.动点M从A点出发,沿折线方向运动,运动到点C停止.设点M的运动路程为x,的面积为y,y与x的函数图象如图2,则AC的长为( )
A.4 B.6 C.8 D.10
10.如图①,为矩形的边上一点,,点从点出发沿折线运动到点停止,点从点出发沿运动到点停止,它们的运动速度都是.现,两点同时出发,设运动时间为,的面积为,若与的对应关系如图②所示,则矩形的面积是( )
A. B. C. D.
二、填空题
11.如图,下列每个三角形中的三个数之间均具有相同的规律,按此规律,最后一个三角形中y与x之间关系的表达式是______.
12.在关系式中,下列说法:①是自变量,是因变量;②的数值可以任意选择;③是变量,它的值与的值无关;④用关系式表示的,不能用图象表示;⑤与的关系还可以用列表法和图象法表示.其中正确的是______.
13.已知海拔每升高1千米,温度下降6℃,某时刻A地底面温度为20℃,高出地面x千米处的温度为y℃,则y与x之间的函数关系为____________.
14.如图,在△ABC中,∠C=90°,BC=8cm,AC=6cm,点E是BC的中点,动点P从A点出发,先以每秒2cm的速度沿A→C运动,然后以1cm/s的速度沿C→B运动.若设点P运动的时间是t秒,那么当t=___________________,△APE的面积等于6.
15.甲、乙两人在一条长400米的直线跑道上同起点、同终点、同方向匀速跑步,先到终点的人原地休息,已知甲先出发3秒,在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,有如下四个结论:①甲的速度是4米/秒;②甲从起点到终点共用80秒;③离开起点后,甲、乙两人第一次相遇时,距离起点30米;④甲、乙两人相距的最大距离为68米.上述所有正确结论的序号是_____.
三、解答题
16.用解析式法与图象法表示等边三角形的周长l关于边长a的函数.
17.如图,一辆快车从甲地驶向乙地,一辆慢车从乙地驶向甲地,设先出发的车辆行驶时间为x(小时),两车之间的距离为y(km),如下的函数图像表示y与x之间的函数关系.
(1)慢车速度为______km/h,快车速度为______km/h.
(2)快车出发多少时间后,两车之间的距离为300km.
18.实验室甲、乙两人相约一起去距二人所在地的市器材店购买器材.两人都从实验室出发,沿一条笔直的公路匀速前往器材店.乙因有事耽搁就让甲骑摩托车先出发,一段时间后乙开车沿同一路线出发,两人都到达器材店后一起购买器材.设甲行驶的时间为,两人之间的距离为.如图表示两人在前往器材店的路上,与函数关系的部分图像.请你解决以下问题:
(1)说明点、点、点的实际意义;
(2)求出甲、乙的速度;
(3)当__________时,两人之间相距8千米?
19.下面的图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又原路返回,顺路到文具店去买笔,然后散步回家.其中x表示时间,y表示张强离家的距离.根据图象回答:
(1)体育场离张强家______千米,张强从家到体育场用了______分钟;
(2)体育场离文具店______千米;
(3)张强在文具店逗留了______分钟.
20.甲乙两地的距离为45千米,下图中的折线表示某骑车人离甲地的距离y(千米)与时间x(时)之间的函数关系.有一辆客车9点从乙地出发,以45千米/小时的速度匀速行驶,并往返于甲乙两地之间(乘客上下车的停留时间忽略不计).
(1)从折线图可以看出,骑车人一共休息_______次,共休息了_________小时;
(2)请在图中画出9点至15点之间客车与甲地的距离y(千米)随时间x(时)变化的函数图象;
(3)由图象可以看出,在_______时,骑车人与客车同时位于________地(填“甲”或“乙”),除此之外的行进过程中,有_____次是骑车人与客车迎面相遇,有________次是客车从背后追上骑车人.
21.已知动点P从点A出发沿图1的边框(边框拐角处都互相垂直)按A→B→C→D→E→F的路径移动,相应的△AHP的面积y(cm2)关于移动路程x(cm)的关系图象如图2,若AH=2cm
(1)图1中AB= cm;
(2)图2中n= ;
(3)求△AHP面积的最大值.
22.如图1,点沿边框以为路径,从到以的速度运动,的面积为与运动时间的关系如图2所示,.
(1)当时,求与运动时间的关系式;
(2)求图2中,的值;
(3)求点在运动过程中的最大值.
23.在弹性限度范围内,弹簧挂上适当的重物后会按一定的规律伸长,已知一弹簧的长度与所挂物体的质量之间的关系如下表:
所挂物体的质量 0 1 2 3 4 5 6
弹簧的长度 14 14.8 15.6 16.4 17.2 18 18.8
(1)上表反映了哪两个变量之间的关系?哪个是自变量?
(2)在弹性限度范围内写出与之间的关系式;
(3)当所挂物体的质量为时(在弹性限度范围内),求弹簧的长度.
(4)在弹性限度范围内,弹簧伸长后的最大长度为,求物体质量的取值范围?
【参考答案】
1.B 2.D 3.D 4.B 5.C 6.D 7.D 8.B 9.B 10.C
11.y=x+2x-2(x≥2)
12.①②⑤
13.y=-6x+20
14.1.5或5或9
15.①④##④①
16.,图象略
17.(1)80,120
(2)快车出发0.7或3.7小时时,两车之间的距离为300km.
18.(1)点所表示的含义为:甲先走20分钟,此时甲乙相距10千米,表示的含义为:乙行驶30分钟追上了甲,此时甲乙两人相遇,表示的含义为:乙行驶70分钟,此时两人相距千米.
(2)甲的速度为每分钟千米,乙的速度为每分钟千米.
(3)当分钟或分钟或分钟或分钟时,两人相距8千米.
19.(1)2.5;15;(2)1;(3)20
20.(1)2,2;(2)略;(3)13,乙,3,1.
21.(1);(2);(3)
22.(1);(2)32,18;(3)
23.(1)所挂物体质量及弹簧长度间的关系;所挂物体质量为自变量;(2)y=14+0.8x;(3)20.8cm;(4)0≤x≤10.
19.1.2 函数的图像 课后练习
一、选择题
1.函数的图象上的点一定在第( )象限
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.在平面直角坐标系中,下列函数的图象经过点的是( )
A. B. C. D.
3.柿子熟了,从树上落下来,下面的哪一幅图可以大致刻画出柿子下落过程中(即落地前)的速度变化情况( )
A. B. C. D.
4.我们要节约用水,平时要关好水龙头.没有关好水龙头,每滴水约0.05毫升,每分钟滴60滴.如果小明忘记关水龙头,则x分钟后,小明浪费的水y(毫升)与时间x(分钟)之间的函数关系是( )
A.y=60x B.y=3x C.y=0.05x D.y=0.05x+60
5.变量x,y的一些对应值如表:
x … ﹣2 ﹣1 0 1 2 3 …
y … 9 2 1 0 ﹣7 ﹣26 …
根据表格中的数据规律,当x=﹣5时,y的值是( )A.76 B.﹣74 C.126 D.﹣124
6.甲、乙两辆汽车在同一条路上匀速行驶,图①和图②表示汽车速度与时间的关系,图③和图④表示汽车路程与时间的关系,小明对4个图中汽车运动的情况进行了描述,其中正确的是( )
A.图①,乙的速度是甲的3倍,相同时间甲乙的路程相等
B.图②,乙的速度是甲的2倍,相同时间乙的路程是甲的一半
C.图③,乙的速度是甲的2倍,相同时间乙的路程是甲的一半
D.图④,乙的速度是甲的2倍,相同时间乙的路程是甲的2倍
7.如图是甲、乙两个动点在某时段速度随时间变化的图象,下列结论错误的是( )
A.乙点前4秒是匀速运动,4秒后速度不断增加 B.甲点比乙点早4秒将速度提升到32cm/s
C.在4至8秒内甲的速度都大于乙的速度 D.甲、乙两点到第3秒时运动的路程相等
8.甲、乙两人同时各接受了600个零件的加工任务,甲比乙每分钟加工的数量多,两人同时开始加工,加工过程中甲因故障停止一会后又继续按原速加工,直到他们完成任务.甲比乙多加工的零件数量(个)与加工时间(分)之间的函数关系如图所示,点的横坐标为12,点的坐标为,点的横坐标为128,则下列说法中不正确的是( )
A.甲每分钟加工的零件数量是5个 B.在60分钟时,甲比乙多加工了120个零件
C.点的横坐标是200 D.的最大值是216
9.如图1,在中,,于点.动点M从A点出发,沿折线方向运动,运动到点C停止.设点M的运动路程为x,的面积为y,y与x的函数图象如图2,则AC的长为( )
A.4 B.6 C.8 D.10
10.如图①,为矩形的边上一点,,点从点出发沿折线运动到点停止,点从点出发沿运动到点停止,它们的运动速度都是.现,两点同时出发,设运动时间为,的面积为,若与的对应关系如图②所示,则矩形的面积是( )
A. B. C. D.
二、填空题
11.如图,下列每个三角形中的三个数之间均具有相同的规律,按此规律,最后一个三角形中y与x之间关系的表达式是______.
12.在关系式中,下列说法:①是自变量,是因变量;②的数值可以任意选择;③是变量,它的值与的值无关;④用关系式表示的,不能用图象表示;⑤与的关系还可以用列表法和图象法表示.其中正确的是______.
13.已知海拔每升高1千米,温度下降6℃,某时刻A地底面温度为20℃,高出地面x千米处的温度为y℃,则y与x之间的函数关系为____________.
14.如图,在△ABC中,∠C=90°,BC=8cm,AC=6cm,点E是BC的中点,动点P从A点出发,先以每秒2cm的速度沿A→C运动,然后以1cm/s的速度沿C→B运动.若设点P运动的时间是t秒,那么当t=___________________,△APE的面积等于6.
15.甲、乙两人在一条长400米的直线跑道上同起点、同终点、同方向匀速跑步,先到终点的人原地休息,已知甲先出发3秒,在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,有如下四个结论:①甲的速度是4米/秒;②甲从起点到终点共用80秒;③离开起点后,甲、乙两人第一次相遇时,距离起点30米;④甲、乙两人相距的最大距离为68米.上述所有正确结论的序号是_____.
三、解答题
16.用解析式法与图象法表示等边三角形的周长l关于边长a的函数.
17.如图,一辆快车从甲地驶向乙地,一辆慢车从乙地驶向甲地,设先出发的车辆行驶时间为x(小时),两车之间的距离为y(km),如下的函数图像表示y与x之间的函数关系.
(1)慢车速度为______km/h,快车速度为______km/h.
(2)快车出发多少时间后,两车之间的距离为300km.
18.实验室甲、乙两人相约一起去距二人所在地的市器材店购买器材.两人都从实验室出发,沿一条笔直的公路匀速前往器材店.乙因有事耽搁就让甲骑摩托车先出发,一段时间后乙开车沿同一路线出发,两人都到达器材店后一起购买器材.设甲行驶的时间为,两人之间的距离为.如图表示两人在前往器材店的路上,与函数关系的部分图像.请你解决以下问题:
(1)说明点、点、点的实际意义;
(2)求出甲、乙的速度;
(3)当__________时,两人之间相距8千米?
19.下面的图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又原路返回,顺路到文具店去买笔,然后散步回家.其中x表示时间,y表示张强离家的距离.根据图象回答:
(1)体育场离张强家______千米,张强从家到体育场用了______分钟;
(2)体育场离文具店______千米;
(3)张强在文具店逗留了______分钟.
20.甲乙两地的距离为45千米,下图中的折线表示某骑车人离甲地的距离y(千米)与时间x(时)之间的函数关系.有一辆客车9点从乙地出发,以45千米/小时的速度匀速行驶,并往返于甲乙两地之间(乘客上下车的停留时间忽略不计).
(1)从折线图可以看出,骑车人一共休息_______次,共休息了_________小时;
(2)请在图中画出9点至15点之间客车与甲地的距离y(千米)随时间x(时)变化的函数图象;
(3)由图象可以看出,在_______时,骑车人与客车同时位于________地(填“甲”或“乙”),除此之外的行进过程中,有_____次是骑车人与客车迎面相遇,有________次是客车从背后追上骑车人.
21.已知动点P从点A出发沿图1的边框(边框拐角处都互相垂直)按A→B→C→D→E→F的路径移动,相应的△AHP的面积y(cm2)关于移动路程x(cm)的关系图象如图2,若AH=2cm
(1)图1中AB= cm;
(2)图2中n= ;
(3)求△AHP面积的最大值.
22.如图1,点沿边框以为路径,从到以的速度运动,的面积为与运动时间的关系如图2所示,.
(1)当时,求与运动时间的关系式;
(2)求图2中,的值;
(3)求点在运动过程中的最大值.
23.在弹性限度范围内,弹簧挂上适当的重物后会按一定的规律伸长,已知一弹簧的长度与所挂物体的质量之间的关系如下表:
所挂物体的质量 0 1 2 3 4 5 6
弹簧的长度 14 14.8 15.6 16.4 17.2 18 18.8
(1)上表反映了哪两个变量之间的关系?哪个是自变量?
(2)在弹性限度范围内写出与之间的关系式;
(3)当所挂物体的质量为时(在弹性限度范围内),求弹簧的长度.
(4)在弹性限度范围内,弹簧伸长后的最大长度为,求物体质量的取值范围?
【参考答案】
1.B 2.D 3.D 4.B 5.C 6.D 7.D 8.B 9.B 10.C
11.y=x+2x-2(x≥2)
12.①②⑤
13.y=-6x+20
14.1.5或5或9
15.①④##④①
16.,图象略
17.(1)80,120
(2)快车出发0.7或3.7小时时,两车之间的距离为300km.
18.(1)点所表示的含义为:甲先走20分钟,此时甲乙相距10千米,表示的含义为:乙行驶30分钟追上了甲,此时甲乙两人相遇,表示的含义为:乙行驶70分钟,此时两人相距千米.
(2)甲的速度为每分钟千米,乙的速度为每分钟千米.
(3)当分钟或分钟或分钟或分钟时,两人相距8千米.
19.(1)2.5;15;(2)1;(3)20
20.(1)2,2;(2)略;(3)13,乙,3,1.
21.(1);(2);(3)
22.(1);(2)32,18;(3)
23.(1)所挂物体质量及弹簧长度间的关系;所挂物体质量为自变量;(2)y=14+0.8x;(3)20.8cm;(4)0≤x≤10.
