人教版七年级数学下册第六章 实数 复习课教案
文档属性
| 名称 | 人教版七年级数学下册第六章 实数 复习课教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 88.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-21 06:42:19 | ||
图片预览

文档简介
《实数》复习课教案
教学目标
1.理解平方根、算术平方根、立方根的概念,能用平方或立方运算求某些数的平方根或立方根;
2.会用计算器进行数的加、减、乘、除、乘方及开方运算;
3.了解无理数的意义,会对实数进行分类,了解实数的相反数和绝对值的意义;
4.了解实数与数轴上的点一一对应,了解有理数的运算律适用于实数范围.会按结果所要求的精确度用近似的有限小数代替无理数进行实数的四则运算.
教学重难点
1.平方根和算术平方根的概念、性质,无理数与实数的意义;
2.算术平方根的意义及实数的性质.
教学过程
一、知识疏理,形成体系(课前要求学生对本章知识进行总结)
师:本章的主要内容是开方运算.从定义出发解题是解本章有关题目的基本方法,我们注意掌握用计算器进行数的计算的方法的同时,还必须注意区分清楚有理数与无理数的概念,掌握实数的四则运算.下面,我们小结一下本章的知识点.
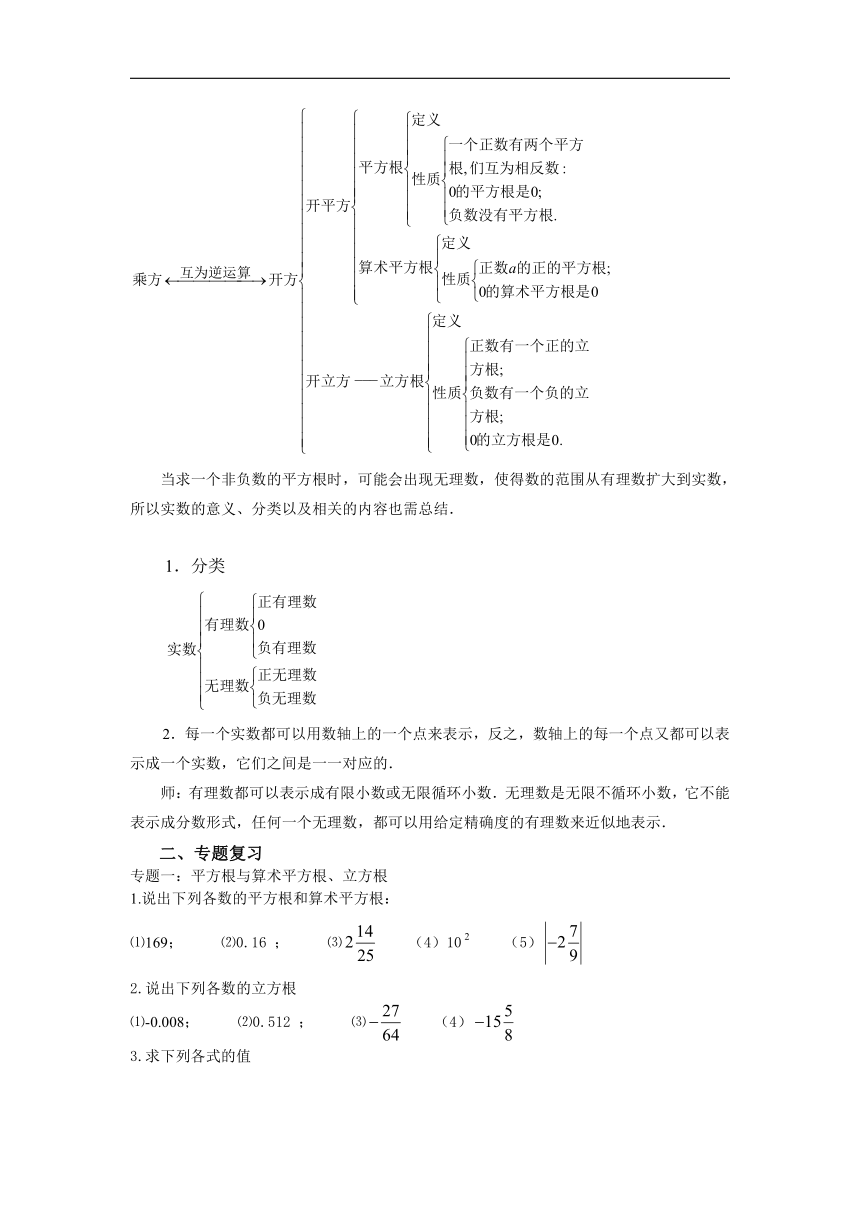
开方包括开平方与开立方.通过开平方可求一个非负实数的平方根;通过开立方可求一个实数的立方根.依据这一思路,我们画出的知识结构图是:
师:好!他们组是以运算为线索总结的,侧重总结了开方运算,还有补充吗?
我们认为平方根、算术平方根、立方根的定义、性质也都非常重要.因此我们是这样总结的:
当求一个非负数的平方根时,可能会出现无理数,使得数的范围从有理数扩大到实数,所以实数的意义、分类以及相关的内容也需总结.
1.分类
2.每一个实数都可以用数轴上的一个点来表示,反之,数轴上的每一个点又都可以表示成一个实数,它们之间是一一对应的.
师:有理数都可以表示成有限小数或无限循环小数.无理数是无限不循环小数,它不能表示成分数形式,任何一个无理数,都可以用给定精确度的有理数来近似地表示.
二、专题复习
专题一:平方根与算术平方根、立方根
1.说出下列各数的平方根和算术平方根:
⑴169; ⑵0.16 ; ⑶ (4)10 (5)
2.说出下列各数的立方根
⑴-0.008; ⑵0.512 ; ⑶ (4)
3.求下列各式的值
⑴; ⑵; ⑶ (4)
专题二:实数的复习
1.把下列各数填入相应的集合内:
,,,,,,,0,,,0.3737737773……(相邻两个之间的7的个数数逐次加1)
有=理数集合{ }
无理数集合{ }
2.判断下列说法是否正确:
(1)实数不是有理数就是无理数。 ( )
(2)无限小数都是无理数。 ( )
(3)无理数都是无限小数。 ( )
(4)带根号的数都是无理数。 ( )
(5)两个无理数之和一定是无理数。( )
(6)所有的有理数都可以在数轴上表示,反过来,数轴上所有的点都表示有理数。( )
专题三:实数的化简求值
1.化简下列各式:
(1) (2) (3) (4)
例1:(1) (2)-
例2:已知0.8183,3.777 ,1.753,则
例3:计算:
2.化简含绝对值符号的式子
例1:
(1).比较大小:-2+与
(2).已知实数在数轴上对应点位置如图
(3)化简
专题四:课后练习
1.计算:
(1)
(2)
2.解方程
(1)
(2)
三、查缺补漏,归纳提升.
1.通过今天的探究学习,你们有哪些收获?
2.非负数的和等于零的条件是:当且仅当每个非负数的值都等于零.此性质在解题时经常会被用到.
3.对于本章的内容你还有那些疑问?
四、课后作业
1.布置作业:从课本“复习题6”中选取.
2.完成练习册中本课时的练习.
五、教学反思
1.本课时教学可应用不同形式的练习引导学生认识相关的基本概念,强化对基本概念的理解以利于进行运算与判断.
2.注重分类思想的认识与理解,强调实数计算能力的训练,
打下坚实的运算能力的基础.
教学目标
1.理解平方根、算术平方根、立方根的概念,能用平方或立方运算求某些数的平方根或立方根;
2.会用计算器进行数的加、减、乘、除、乘方及开方运算;
3.了解无理数的意义,会对实数进行分类,了解实数的相反数和绝对值的意义;
4.了解实数与数轴上的点一一对应,了解有理数的运算律适用于实数范围.会按结果所要求的精确度用近似的有限小数代替无理数进行实数的四则运算.
教学重难点
1.平方根和算术平方根的概念、性质,无理数与实数的意义;
2.算术平方根的意义及实数的性质.
教学过程
一、知识疏理,形成体系(课前要求学生对本章知识进行总结)
师:本章的主要内容是开方运算.从定义出发解题是解本章有关题目的基本方法,我们注意掌握用计算器进行数的计算的方法的同时,还必须注意区分清楚有理数与无理数的概念,掌握实数的四则运算.下面,我们小结一下本章的知识点.
开方包括开平方与开立方.通过开平方可求一个非负实数的平方根;通过开立方可求一个实数的立方根.依据这一思路,我们画出的知识结构图是:
师:好!他们组是以运算为线索总结的,侧重总结了开方运算,还有补充吗?
我们认为平方根、算术平方根、立方根的定义、性质也都非常重要.因此我们是这样总结的:
当求一个非负数的平方根时,可能会出现无理数,使得数的范围从有理数扩大到实数,所以实数的意义、分类以及相关的内容也需总结.
1.分类
2.每一个实数都可以用数轴上的一个点来表示,反之,数轴上的每一个点又都可以表示成一个实数,它们之间是一一对应的.
师:有理数都可以表示成有限小数或无限循环小数.无理数是无限不循环小数,它不能表示成分数形式,任何一个无理数,都可以用给定精确度的有理数来近似地表示.
二、专题复习
专题一:平方根与算术平方根、立方根
1.说出下列各数的平方根和算术平方根:
⑴169; ⑵0.16 ; ⑶ (4)10 (5)
2.说出下列各数的立方根
⑴-0.008; ⑵0.512 ; ⑶ (4)
3.求下列各式的值
⑴; ⑵; ⑶ (4)
专题二:实数的复习
1.把下列各数填入相应的集合内:
,,,,,,,0,,,0.3737737773……(相邻两个之间的7的个数数逐次加1)
有=理数集合{ }
无理数集合{ }
2.判断下列说法是否正确:
(1)实数不是有理数就是无理数。 ( )
(2)无限小数都是无理数。 ( )
(3)无理数都是无限小数。 ( )
(4)带根号的数都是无理数。 ( )
(5)两个无理数之和一定是无理数。( )
(6)所有的有理数都可以在数轴上表示,反过来,数轴上所有的点都表示有理数。( )
专题三:实数的化简求值
1.化简下列各式:
(1) (2) (3) (4)
例1:(1) (2)-
例2:已知0.8183,3.777 ,1.753,则
例3:计算:
2.化简含绝对值符号的式子
例1:
(1).比较大小:-2+与
(2).已知实数在数轴上对应点位置如图
(3)化简
专题四:课后练习
1.计算:
(1)
(2)
2.解方程
(1)
(2)
三、查缺补漏,归纳提升.
1.通过今天的探究学习,你们有哪些收获?
2.非负数的和等于零的条件是:当且仅当每个非负数的值都等于零.此性质在解题时经常会被用到.
3.对于本章的内容你还有那些疑问?
四、课后作业
1.布置作业:从课本“复习题6”中选取.
2.完成练习册中本课时的练习.
五、教学反思
1.本课时教学可应用不同形式的练习引导学生认识相关的基本概念,强化对基本概念的理解以利于进行运算与判断.
2.注重分类思想的认识与理解,强调实数计算能力的训练,
打下坚实的运算能力的基础.
