青岛版小学四年级数学上册《智慧广场——植树问题》教学设计
文档属性
| 名称 | 青岛版小学四年级数学上册《智慧广场——植树问题》教学设计 |  | |
| 格式 | doc | ||
| 文件大小 | 411.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-20 15:57:26 | ||
图片预览


文档简介
《智慧广场——植树问题》教学设计
教学内容:四年级上册P106~107智慧广场及练习。
教材分析:
“植树问题”是四年级上册“智慧广场”的教学内容。植树问题可以分为不封闭植树问题和封闭植树问题两类情况,而不封闭的植树问题又可以分为一条线段上的两端都栽、只栽一端和两端不栽三种情况。本节课就着重探讨在一条线段上植树时三种情况下棵数与问隔数之间的关系。
教学目标:
1.了解在一条线段上植树问题的三种基本情况,能阐述不同情况下棵数与间隔数的关系,并能根据不同情况选择正确方法解决问题。
2.通过小组合作、观察、举例、画图等活动,探索出棵数与间隔数之间的规律,从而建立植树问题的数学模型。在学生探究过程中渗透数形结合的数学思想与方法,培养学生的推理能力。
3.在解决实际问题中感受数学的价值,体会数学与日常生活的联系。
教学重点:能阐述不同情况下棵数与间隔数的关系。
教学难点:能根据不同情况选择正确方法解决问题。
教学过程:
活动一:创设情境,感知规律。
课件出示:学校门前有一条长50米的小路,计划在小路的一边植树,每5米栽一棵。
师:要想知道能栽多少棵树,请同学们想一想,你还需要了解哪些信息?
生1:每隔多少米栽一棵树?
生2:是两端都栽还是什么情况?
师:植树确实需要知道每隔多少米栽一棵,也就是要知道相邻两棵树之间的间隔是多少。现在告诉你们,每隔5米栽一棵。老师邀请你来做个小小设计师,帮学校设计出一份植树方案,你愿意吗?
生:愿意。
师:请同学们拿出一号张纸,把你的植树方案画出来。
___同学的植树方案:我的设计需要( )棵树。我是这样设计的:
学生思考、操作,教师巡视。
师:哪位小设计师愿意把你的设计方案给大家展示一下并解释给大家听听?
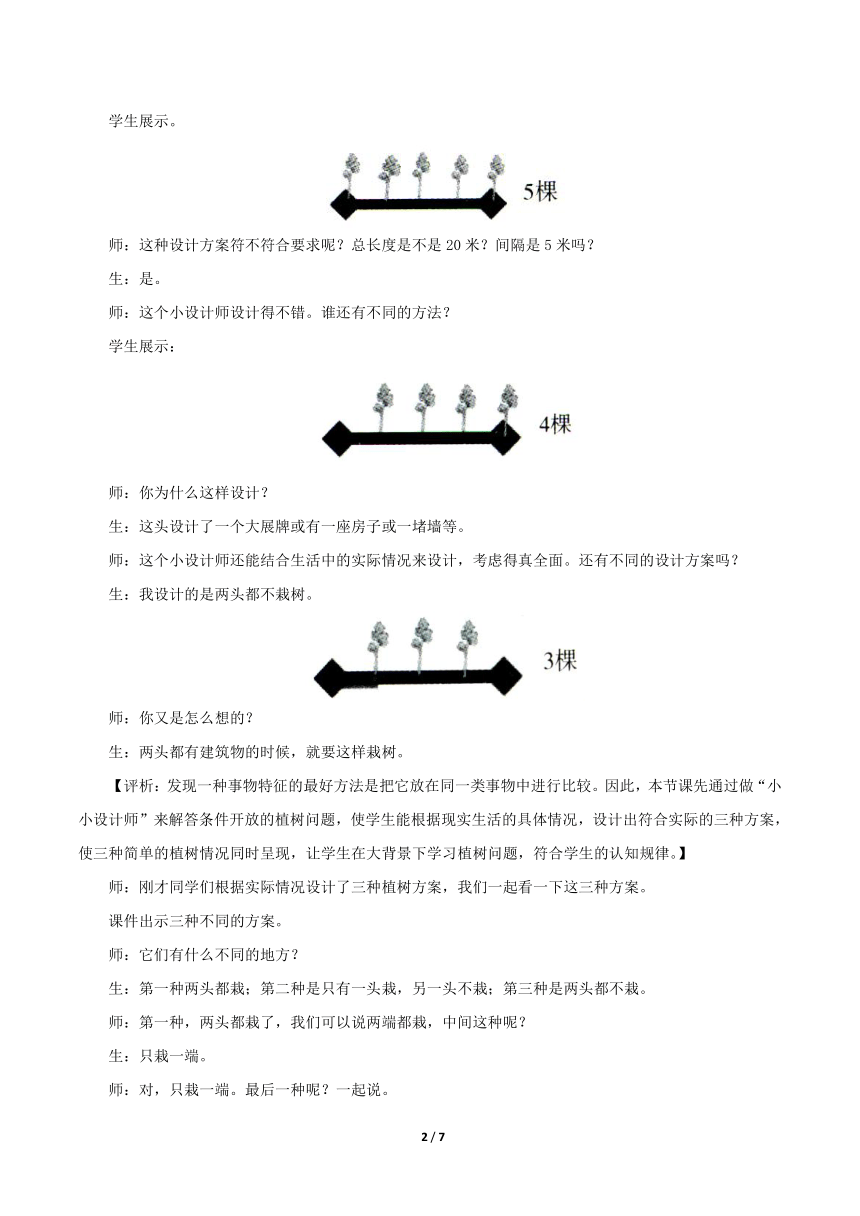
学生展示。
师:这种设计方案符不符合要求呢?总长度是不是20米?间隔是5米吗?
生:是。
师:这个小设计师设计得不错。谁还有不同的方法?
学生展示:
师:你为什么这样设计?
生:这头设计了一个大展牌或有一座房子或一堵墙等。
师:这个小设计师还能结合生活中的实际情况来设计,考虑得真全面。还有不同的设计方案吗?
生:我设计的是两头都不栽树。
师:你又是怎么想的?
生:两头都有建筑物的时候,就要这样栽树。
【评析:发现一种事物特征的最好方法是把它放在同一类事物中进行比较。因此,本节课先通过做“小小设计师”来解答条件开放的植树问题,使学生能根据现实生活的具体情况,设计出符合实际的三种方案,使三种简单的植树情况同时呈现,让学生在大背景下学习植树问题,符合学生的认知规律。】
师:刚才同学们根据实际情况设计了三种植树方案,我们一起看一下这三种方案。
课件出示三种不同的方案。
师:它们有什么不同的地方?
生:第一种两头都栽;第二种是只有一头栽,另一头不栽;第三种是两头都不栽。
师:第一种,两头都栽了,我们可以说两端都栽,中间这种呢?
生:只栽一端。
师:对,只栽一端。最后一种呢?一起说。
生:两端都不栽。
教师板书三种情况。
师:继续观察,这三种情况有什么相同的地方?
生1:都是每隔5米栽一棵。
生2:中间都栽了3棵。
生3:都有4个间隔。
师:大家真善于观察。咱们一起来看,这三种不同的栽法,都有4个间隔(屏幕闪动4个间隔),棵数却不同。看来间隔数与棵数有紧密的联系,到底它们之间有什么关系呢?能不能大胆地猜一猜?
生:只栽一端时,棵数=间隔数。
生2:两端都栽时,棵数比间隔数多1。
生3:两端都不栽时,棵数比间隔数少1。
【评析:小学生的推理能力主要表现在:能通过观察、归纳、类比等获得数学猜想,并进一步寻求证据、给出证明。因此,这样在学生设计了三种植树方案的基础上,让学生观察研究这些素材,大胆猜想这些情况下棵数与间隔数存在的规律,使学生经历“猜想、验证、结论”的学习过程,有利于培养学生的推理能力。】
活动二:探索交流,验证规律。
师:同学们到底猜测得对不对呢?下面我们就想办法验证一下。现在,我们以两端都栽这种情况为例,以小组为单位,可以用你喜欢的方法,如果感到有困难,也可以利用老师给你提供的表格。我们来验证一下间隔数与棵数到底存在什么关系。小组长负责把你们的方法和结论记录下来。
学生汇报交流验证情况。
生1:我们借助表格,举出具体的数,并用线段图的方法来验证了两端都栽时,棵数就比间隔数多1。
师:刚才这个小组列举了大量的数据,通过画线段图,发现了两端都栽的情况下,棵数比间隔数多l。
生2:我们是用手指代表树来验证的。当两端都栽时,树的棵数比间隔数多1。
师:这个小组还想到用我们的手来验证间隔数与棵数的关系,不错。
生3:我们是借助线段图来证明的。有两个间隔时,就能栽3棵树,有3个间隔时,栽4棵树,有4个间隔时,栽5棵树。树的棵数总是比间隔数多1。
师:这个小组没有用具体的数据,直接用简单的线段图也发现了间隔数与棵数的关系,你们觉得这种方法怎样?
生:简单清楚。
师:你也用这种方法画画看。
学生画。
师:刚才同学们用了不同的方法来验证了两端都栽的情况下间隔数与棵数的关系。谁能再说一下?
生:棵数比间隔数多1,间隔数比棵数少1。
师:棵数比间隔数多1,间隔数比棵数少1,我们用一个等式怎样表示?
生:棵数=间隔数+1
板书:棵数=间隔数+1
师:那现在如果有8个间隔,几棵树?怎么算?
生:9棵。8+1=9。
师:10个间隔呢?对,11棵树。那20棵树有几个间隔?
生:19个间隔。
师:100棵树呢?
生:99个间隔。
师:我们已经验证了两端都栽的情况下棵数与间隔数的关系,由两端都栽的情况我们可不可以推算出其他两种情况下棵数与间隔数的关系呢?
生:只栽一端时,棵数=间隔数。两端都不栽时,棵数=间隔数-1。
师:大家同意吗?真了不起,由两端都栽的情况下棵数与间隔数的关系直接推出了另外的两种情况。
板书:只栽一端时,棵数=间隔数。两端都不栽时,棵数=间隔数-1。
师:同学们看,间隔数与棵数的关系与我们刚才的猜测一样吗?
生:一样。
师:同学们真了不起,先大胆猜想,又想办法验证了自己的猜想,从而得出了在不同情况下棵数与间隔数之间的规律。现在谁能完整地说一说?
生说。
【评析:学生的数学学习活动应该是学生去自主探究,发现规律。因此,在学生已经初步感知棵数与间隔数存在一定关系的基础上,教师应充分放手,让学生通过自己的思考、分析、操作、推理、验证、解释、归纳这一系列的活动经历,通过丰富的材料,自己总结出棵数与间隔数之间的规律,并充分感悟到数形结合的数学思想。然后,学生由两端都栽的情况存在的规律再推延到另外两种情况的规律,顺理成章。】
活动三:总结方法,创设模型。
师:这三种情况我们能不能用算式表示出来呢?先看这一种,只栽一端的。用算式怎样表示?
生:20÷5=4(棵)
师:你是怎样想的?
生:20里面有4个5,就是有4个间隔。
师:有4个间隔为什么就等于4棵树?
生:只栽一端时,间隔数=棵数。
师:再看两端都栽这种情况,怎样列式?
生:20÷5+1=5(棵)。
师:告诉大家20÷5求的是什么?为什么要加1?
生:20÷5求的是间隔数。因为两端都栽时,棵数=间隔数+1,所以要加上1。
师:第三种呢?用算式怎样表达?
师:现在谁能告诉大家,要解决植树问题我们首先要明确什么?然后呢?
生:要先判断属于哪种情况,然后求出间隔数,最后根据实际情况确定加1还是减1,还是不加不减。
师:的确,我们在解决植树问题时,一定要先判断属于哪种情况,然后求出间隔数,最后根据实际情况确定加1还是减l,还是不加不减。
【评析:学生在自己探索出“植树规律”后,通过独立列式,发现共同点,从而自主建构起解决植树问题的数学模型。】
活动四:联系生活,应用模型。
师:刚刚我们一起研究了植树问题。其实在我们的现实生活中,有很多现象类似于我们今天学习的植树问题,你能说说看吗?
生1:安装路灯。
生2:锯木头时,锯的段数和锯的次数的关系。
师:下面我们就一起用我们今天学到的知识来解决这些实际问题。
出示:1.在一条全长180米的街道一旁安装路灯(两端都要安装),每隔6米安一座,一共要安装多少座路灯?
学生读题并列式计算。
师:谁来说说你是怎么算的?
生:180÷6+1=31(座)
师:能说说你是怎么想的吗?
生:先算出有多少个间隔,因为两端都要安装,所以再加l。
师:大家同意吗?
生:同意。
师:来,继续看。
出示:2.希望小学两栋教学楼之间相距150米,为了迎接“六一”儿童节,学校计划在这两栋楼之间插上彩旗,每隔5米插一面,二共需要多少面彩旗?
师:怎样列式计算?
生:150÷5=30(面),30-1=29(面)。
师:为什么要减1?
生:因为两端是大楼,都不需要插旗,所以要减l。
出示:3.每走一层楼有18个台阶,老师从1楼去4楼某教室,共走了多个台阶?
(1)18×4 (2)18×(4-1) (3)18×(4+1)
师:这个问题我们可不可以看做植树问题呢?想一想应该选择哪个算式?为什么?
先把你的想法和小组里的同学交流一下。
师:谁来说一说?
生:从1楼到4楼等于有3个间隔,每个间隔18个台阶,所以用18×(4-1)。
师:前面我们研究的都是在一条直线上植树,其实植树还有可能是这种情况。屏幕展示沿圆形池塘栽树和沿正方形边线植树的情况。
师:大家看,沿着圆形池塘植树,或围成一个正方形等,这种情况下棵数与间隔数又有什么关系呢?这个问题,我们下节课继续研究。
【评析:先是让学生用数学的眼光观察生活,找一找生活中类似植树问题的现象,并思考可以把什么看作“树”,培养学生化归的数学思想,感悟生活中“模”的存在,再让学生独立解决一些数学问题,感受到“数学模型”的力量,并体验到数学与生活的联系。植树问题可以分为不封闭植树问题和封闭植树问题两类情况,今天只是研究的不封闭植树这类情况。为一了给学生一个完整的知识系统,在课尾预留一个封闭植树的问题,既完善了知识框架,又给学生留下了广阔的思维空间,激发他们继续探究的欲望。】
活动五:课堂总结。
师:这节课你有哪些收获?
生1:我知道了在一条直线上植树问题的三种情况:两端都栽、只栽一端、两端都不栽,知道了三种情况下棵数与间隔数的关系。
生2:通过观察、举例、验证,自己探索出了棵数与间隔数之间的规律,我很开心。
……
【评析:通过回顾所学的知识,学生获得数学知识的同时,提升梳理、概括知识的能力。这样能使学生在交流中巩固新知,进一步体会数学与生活的密切联系,激发学生学习的热情,使学生的情感得到进一步的升华。】
1 / 7
教学内容:四年级上册P106~107智慧广场及练习。
教材分析:
“植树问题”是四年级上册“智慧广场”的教学内容。植树问题可以分为不封闭植树问题和封闭植树问题两类情况,而不封闭的植树问题又可以分为一条线段上的两端都栽、只栽一端和两端不栽三种情况。本节课就着重探讨在一条线段上植树时三种情况下棵数与问隔数之间的关系。
教学目标:
1.了解在一条线段上植树问题的三种基本情况,能阐述不同情况下棵数与间隔数的关系,并能根据不同情况选择正确方法解决问题。
2.通过小组合作、观察、举例、画图等活动,探索出棵数与间隔数之间的规律,从而建立植树问题的数学模型。在学生探究过程中渗透数形结合的数学思想与方法,培养学生的推理能力。
3.在解决实际问题中感受数学的价值,体会数学与日常生活的联系。
教学重点:能阐述不同情况下棵数与间隔数的关系。
教学难点:能根据不同情况选择正确方法解决问题。
教学过程:
活动一:创设情境,感知规律。
课件出示:学校门前有一条长50米的小路,计划在小路的一边植树,每5米栽一棵。
师:要想知道能栽多少棵树,请同学们想一想,你还需要了解哪些信息?
生1:每隔多少米栽一棵树?
生2:是两端都栽还是什么情况?
师:植树确实需要知道每隔多少米栽一棵,也就是要知道相邻两棵树之间的间隔是多少。现在告诉你们,每隔5米栽一棵。老师邀请你来做个小小设计师,帮学校设计出一份植树方案,你愿意吗?
生:愿意。
师:请同学们拿出一号张纸,把你的植树方案画出来。
___同学的植树方案:我的设计需要( )棵树。我是这样设计的:
学生思考、操作,教师巡视。
师:哪位小设计师愿意把你的设计方案给大家展示一下并解释给大家听听?
学生展示。
师:这种设计方案符不符合要求呢?总长度是不是20米?间隔是5米吗?
生:是。
师:这个小设计师设计得不错。谁还有不同的方法?
学生展示:
师:你为什么这样设计?
生:这头设计了一个大展牌或有一座房子或一堵墙等。
师:这个小设计师还能结合生活中的实际情况来设计,考虑得真全面。还有不同的设计方案吗?
生:我设计的是两头都不栽树。
师:你又是怎么想的?
生:两头都有建筑物的时候,就要这样栽树。
【评析:发现一种事物特征的最好方法是把它放在同一类事物中进行比较。因此,本节课先通过做“小小设计师”来解答条件开放的植树问题,使学生能根据现实生活的具体情况,设计出符合实际的三种方案,使三种简单的植树情况同时呈现,让学生在大背景下学习植树问题,符合学生的认知规律。】
师:刚才同学们根据实际情况设计了三种植树方案,我们一起看一下这三种方案。
课件出示三种不同的方案。
师:它们有什么不同的地方?
生:第一种两头都栽;第二种是只有一头栽,另一头不栽;第三种是两头都不栽。
师:第一种,两头都栽了,我们可以说两端都栽,中间这种呢?
生:只栽一端。
师:对,只栽一端。最后一种呢?一起说。
生:两端都不栽。
教师板书三种情况。
师:继续观察,这三种情况有什么相同的地方?
生1:都是每隔5米栽一棵。
生2:中间都栽了3棵。
生3:都有4个间隔。
师:大家真善于观察。咱们一起来看,这三种不同的栽法,都有4个间隔(屏幕闪动4个间隔),棵数却不同。看来间隔数与棵数有紧密的联系,到底它们之间有什么关系呢?能不能大胆地猜一猜?
生:只栽一端时,棵数=间隔数。
生2:两端都栽时,棵数比间隔数多1。
生3:两端都不栽时,棵数比间隔数少1。
【评析:小学生的推理能力主要表现在:能通过观察、归纳、类比等获得数学猜想,并进一步寻求证据、给出证明。因此,这样在学生设计了三种植树方案的基础上,让学生观察研究这些素材,大胆猜想这些情况下棵数与间隔数存在的规律,使学生经历“猜想、验证、结论”的学习过程,有利于培养学生的推理能力。】
活动二:探索交流,验证规律。
师:同学们到底猜测得对不对呢?下面我们就想办法验证一下。现在,我们以两端都栽这种情况为例,以小组为单位,可以用你喜欢的方法,如果感到有困难,也可以利用老师给你提供的表格。我们来验证一下间隔数与棵数到底存在什么关系。小组长负责把你们的方法和结论记录下来。
学生汇报交流验证情况。
生1:我们借助表格,举出具体的数,并用线段图的方法来验证了两端都栽时,棵数就比间隔数多1。
师:刚才这个小组列举了大量的数据,通过画线段图,发现了两端都栽的情况下,棵数比间隔数多l。
生2:我们是用手指代表树来验证的。当两端都栽时,树的棵数比间隔数多1。
师:这个小组还想到用我们的手来验证间隔数与棵数的关系,不错。
生3:我们是借助线段图来证明的。有两个间隔时,就能栽3棵树,有3个间隔时,栽4棵树,有4个间隔时,栽5棵树。树的棵数总是比间隔数多1。
师:这个小组没有用具体的数据,直接用简单的线段图也发现了间隔数与棵数的关系,你们觉得这种方法怎样?
生:简单清楚。
师:你也用这种方法画画看。
学生画。
师:刚才同学们用了不同的方法来验证了两端都栽的情况下间隔数与棵数的关系。谁能再说一下?
生:棵数比间隔数多1,间隔数比棵数少1。
师:棵数比间隔数多1,间隔数比棵数少1,我们用一个等式怎样表示?
生:棵数=间隔数+1
板书:棵数=间隔数+1
师:那现在如果有8个间隔,几棵树?怎么算?
生:9棵。8+1=9。
师:10个间隔呢?对,11棵树。那20棵树有几个间隔?
生:19个间隔。
师:100棵树呢?
生:99个间隔。
师:我们已经验证了两端都栽的情况下棵数与间隔数的关系,由两端都栽的情况我们可不可以推算出其他两种情况下棵数与间隔数的关系呢?
生:只栽一端时,棵数=间隔数。两端都不栽时,棵数=间隔数-1。
师:大家同意吗?真了不起,由两端都栽的情况下棵数与间隔数的关系直接推出了另外的两种情况。
板书:只栽一端时,棵数=间隔数。两端都不栽时,棵数=间隔数-1。
师:同学们看,间隔数与棵数的关系与我们刚才的猜测一样吗?
生:一样。
师:同学们真了不起,先大胆猜想,又想办法验证了自己的猜想,从而得出了在不同情况下棵数与间隔数之间的规律。现在谁能完整地说一说?
生说。
【评析:学生的数学学习活动应该是学生去自主探究,发现规律。因此,在学生已经初步感知棵数与间隔数存在一定关系的基础上,教师应充分放手,让学生通过自己的思考、分析、操作、推理、验证、解释、归纳这一系列的活动经历,通过丰富的材料,自己总结出棵数与间隔数之间的规律,并充分感悟到数形结合的数学思想。然后,学生由两端都栽的情况存在的规律再推延到另外两种情况的规律,顺理成章。】
活动三:总结方法,创设模型。
师:这三种情况我们能不能用算式表示出来呢?先看这一种,只栽一端的。用算式怎样表示?
生:20÷5=4(棵)
师:你是怎样想的?
生:20里面有4个5,就是有4个间隔。
师:有4个间隔为什么就等于4棵树?
生:只栽一端时,间隔数=棵数。
师:再看两端都栽这种情况,怎样列式?
生:20÷5+1=5(棵)。
师:告诉大家20÷5求的是什么?为什么要加1?
生:20÷5求的是间隔数。因为两端都栽时,棵数=间隔数+1,所以要加上1。
师:第三种呢?用算式怎样表达?
师:现在谁能告诉大家,要解决植树问题我们首先要明确什么?然后呢?
生:要先判断属于哪种情况,然后求出间隔数,最后根据实际情况确定加1还是减1,还是不加不减。
师:的确,我们在解决植树问题时,一定要先判断属于哪种情况,然后求出间隔数,最后根据实际情况确定加1还是减l,还是不加不减。
【评析:学生在自己探索出“植树规律”后,通过独立列式,发现共同点,从而自主建构起解决植树问题的数学模型。】
活动四:联系生活,应用模型。
师:刚刚我们一起研究了植树问题。其实在我们的现实生活中,有很多现象类似于我们今天学习的植树问题,你能说说看吗?
生1:安装路灯。
生2:锯木头时,锯的段数和锯的次数的关系。
师:下面我们就一起用我们今天学到的知识来解决这些实际问题。
出示:1.在一条全长180米的街道一旁安装路灯(两端都要安装),每隔6米安一座,一共要安装多少座路灯?
学生读题并列式计算。
师:谁来说说你是怎么算的?
生:180÷6+1=31(座)
师:能说说你是怎么想的吗?
生:先算出有多少个间隔,因为两端都要安装,所以再加l。
师:大家同意吗?
生:同意。
师:来,继续看。
出示:2.希望小学两栋教学楼之间相距150米,为了迎接“六一”儿童节,学校计划在这两栋楼之间插上彩旗,每隔5米插一面,二共需要多少面彩旗?
师:怎样列式计算?
生:150÷5=30(面),30-1=29(面)。
师:为什么要减1?
生:因为两端是大楼,都不需要插旗,所以要减l。
出示:3.每走一层楼有18个台阶,老师从1楼去4楼某教室,共走了多个台阶?
(1)18×4 (2)18×(4-1) (3)18×(4+1)
师:这个问题我们可不可以看做植树问题呢?想一想应该选择哪个算式?为什么?
先把你的想法和小组里的同学交流一下。
师:谁来说一说?
生:从1楼到4楼等于有3个间隔,每个间隔18个台阶,所以用18×(4-1)。
师:前面我们研究的都是在一条直线上植树,其实植树还有可能是这种情况。屏幕展示沿圆形池塘栽树和沿正方形边线植树的情况。
师:大家看,沿着圆形池塘植树,或围成一个正方形等,这种情况下棵数与间隔数又有什么关系呢?这个问题,我们下节课继续研究。
【评析:先是让学生用数学的眼光观察生活,找一找生活中类似植树问题的现象,并思考可以把什么看作“树”,培养学生化归的数学思想,感悟生活中“模”的存在,再让学生独立解决一些数学问题,感受到“数学模型”的力量,并体验到数学与生活的联系。植树问题可以分为不封闭植树问题和封闭植树问题两类情况,今天只是研究的不封闭植树这类情况。为一了给学生一个完整的知识系统,在课尾预留一个封闭植树的问题,既完善了知识框架,又给学生留下了广阔的思维空间,激发他们继续探究的欲望。】
活动五:课堂总结。
师:这节课你有哪些收获?
生1:我知道了在一条直线上植树问题的三种情况:两端都栽、只栽一端、两端都不栽,知道了三种情况下棵数与间隔数的关系。
生2:通过观察、举例、验证,自己探索出了棵数与间隔数之间的规律,我很开心。
……
【评析:通过回顾所学的知识,学生获得数学知识的同时,提升梳理、概括知识的能力。这样能使学生在交流中巩固新知,进一步体会数学与生活的密切联系,激发学生学习的热情,使学生的情感得到进一步的升华。】
1 / 7
