六年级数学下册课件 5 数学广角——鸽巢问题(人教版)(共29张PPT)
文档属性
| 名称 | 六年级数学下册课件 5 数学广角——鸽巢问题(人教版)(共29张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-20 00:00:00 | ||
图片预览








文档简介
(共29张PPT)
游戏:“你放我猜”,把3颗糖放入2个盘子中,老师总能猜对。
师语:总有一个盘子里至少要放2颗糖
注:我们把(2,1)和(1,2)看成是同一种摆法,就是一个盘子有2颗,另一个盘子里有1颗的摆法。
鸽巢原理一(抽屉原理一)
人教版数学六年级下册数学广角
细心观察+留心发现=伟大的发现
1、学生要经历(“鸽巢原理一”)“抽屉原理一”的形成过程。
2、学生要理解“抽屉原理一”(“鸽巢原理一”)的基本形式。
3、学生能初步运用“抽屉原理一”(“鸽巢原理一”)解决相关的实际问题或解释相关现象。
学习目标
世界级难题
据说数学家厄尔多斯一次专程去布达佩斯看望匈牙利的数学神童波沙,给他出了一道题:
在1,2,3,……,2n这2n个自然数中,任意取出n+1个数,其中一定有两个互质数。
利用了鸽巢原理(抽屉原理)
活动一:
把4支铅笔放入3个笔筒里。
请在练习纸上画一画,用圆圈表示笔筒,用竖线表示铅笔。(列举法)
注意:不考虑摆放的顺序
探究新知
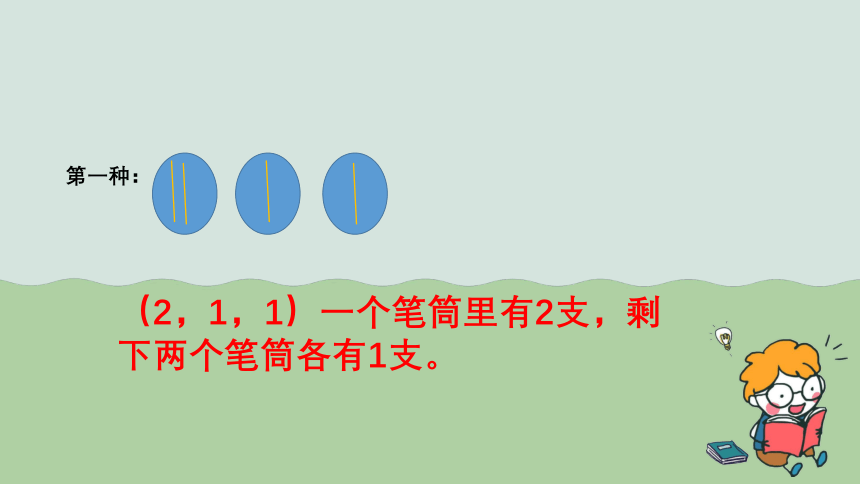
第一种:
(2,1,1)一个笔筒里有2支,剩下两个笔筒各有1支。
第二种:
(2,2,0)两个笔筒里各有2支,剩余一个笔筒1支也没有。
第三种:
(3,1,0)一个笔筒里有3支,另一个笔筒里有1支,剩下一个笔筒1支也没有。
第四种:
(4,0,0)一个笔筒里有4支,剩下两个笔筒一支也没有。
你有什么发现?
方法一:(2,1,1)
方法二:(2,2,0)
方法三:(3,1,0)
方法四:(4,0,0)
总有一个笔筒里至少放2支铅笔
列举法
把4支铅笔放进3个笔筒里
如果每个笔筒里放1支铅笔,最多放( )支铅笔,剩下的( )支铅笔,还要放进其中一个笔筒里,所以,总有一个笔筒里至少放( )支铅笔。
3
1
2
这样的方法,能更好的说明,总有一个笔筒至少要放两支铅笔。
铅笔数(支) 笔筒数(个) 总有一个笔筒里至少放2支铅笔
4 3
5 4
6 5
7 6
8 7
…… ……
n+1 n
二、提升思维,构建模型
结论:把(n+1)支铅笔放进n个笔筒里,总有一个笔筒里至少放进2支铅笔。
“ 抽屉原理”又称“鸽笼原理”,最先是由19世纪的德国数学家狄利克雷提出来的,后来人们为了纪念他从这么平凡的事情中发现的规律,就把这个规律用他的名字命名所以又称“狄利克雷原理”,这一原理在解决实际问题中有着广泛的应用。
(1)把5本书放进4个抽屉里,不管怎么放总有一个抽屉里至少有( )本书。
小练习
(2)7只鸽子飞回6个鸽舍,至少有2只鸽子要飞进同一个鸽舍里,为什么?
在有些问题中,“铅笔”和“杯子”不是很明显, 需要我们制造出“铅笔”和“杯子”
三个
性别
(3)三个朋友同行,其中必有两个小朋友性别相同。
小朋友
(4)一盒围棋棋子,黑白子混放,我们任意摸出3个棋子,至少有2个棋子是同颜色的,为什么?
黑色、白色相当于杯子或者抽屉
3个棋子就相当于是3枝铅笔或者3本书
(5) 任意13人中,总有至少几个人的属相相同,想一想,为什么?
提示:属相只有12个,13个人中即便12个人都是不同的属相,最后一个人的属相必然与其中一个人属相相同。因此,总有至少2个人的属相相同。
(6)一副扑克牌取出大小王,还剩52张牌,5个人每人随意抽一张,总有2张牌的花色相同,为什么?
讨论
5只鸽子飞进了3个鸽笼,总有一个鸽笼至少飞进了2只鸽子,为什么?
(1)把9个苹果放进6个抽屉里,总有一个抽屉至少有( )个苹果。
(2)把11只鸽子放进7个鸽巢,总有一个鸽巢至少有( )个鸽子。
练习2
2
2
世界级难题的简化版:
在1,2,3,……,10这10个自然数中,任意取出6个数,其中一定有两个互质数。
在1,2,3,4,5,6……,2n这2n个自然数中,任意取出n+1个数,其中一定有两个互质数。
试一试,你能行!
思考题:在1,2,3,……,2n这2n个自然数中,任意取出n+1
个数,其中一定有两个互质数。
提示:将相邻两个数作为一组,2n个数就有n组数,可以在n组数中任意取其中一个数,就取得了n个数,第n+1个数可以从n组数中任意一组中取出,此时,在这取出的数中,必然有两个数是相邻的数,而相邻的两个数就是互质数。
你有哪些收获?
再见
游戏:“你放我猜”,把3颗糖放入2个盘子中,老师总能猜对。
师语:总有一个盘子里至少要放2颗糖
注:我们把(2,1)和(1,2)看成是同一种摆法,就是一个盘子有2颗,另一个盘子里有1颗的摆法。
鸽巢原理一(抽屉原理一)
人教版数学六年级下册数学广角
细心观察+留心发现=伟大的发现
1、学生要经历(“鸽巢原理一”)“抽屉原理一”的形成过程。
2、学生要理解“抽屉原理一”(“鸽巢原理一”)的基本形式。
3、学生能初步运用“抽屉原理一”(“鸽巢原理一”)解决相关的实际问题或解释相关现象。
学习目标
世界级难题
据说数学家厄尔多斯一次专程去布达佩斯看望匈牙利的数学神童波沙,给他出了一道题:
在1,2,3,……,2n这2n个自然数中,任意取出n+1个数,其中一定有两个互质数。
利用了鸽巢原理(抽屉原理)
活动一:
把4支铅笔放入3个笔筒里。
请在练习纸上画一画,用圆圈表示笔筒,用竖线表示铅笔。(列举法)
注意:不考虑摆放的顺序
探究新知
第一种:
(2,1,1)一个笔筒里有2支,剩下两个笔筒各有1支。
第二种:
(2,2,0)两个笔筒里各有2支,剩余一个笔筒1支也没有。
第三种:
(3,1,0)一个笔筒里有3支,另一个笔筒里有1支,剩下一个笔筒1支也没有。
第四种:
(4,0,0)一个笔筒里有4支,剩下两个笔筒一支也没有。
你有什么发现?
方法一:(2,1,1)
方法二:(2,2,0)
方法三:(3,1,0)
方法四:(4,0,0)
总有一个笔筒里至少放2支铅笔
列举法
把4支铅笔放进3个笔筒里
如果每个笔筒里放1支铅笔,最多放( )支铅笔,剩下的( )支铅笔,还要放进其中一个笔筒里,所以,总有一个笔筒里至少放( )支铅笔。
3
1
2
这样的方法,能更好的说明,总有一个笔筒至少要放两支铅笔。
铅笔数(支) 笔筒数(个) 总有一个笔筒里至少放2支铅笔
4 3
5 4
6 5
7 6
8 7
…… ……
n+1 n
二、提升思维,构建模型
结论:把(n+1)支铅笔放进n个笔筒里,总有一个笔筒里至少放进2支铅笔。
“ 抽屉原理”又称“鸽笼原理”,最先是由19世纪的德国数学家狄利克雷提出来的,后来人们为了纪念他从这么平凡的事情中发现的规律,就把这个规律用他的名字命名所以又称“狄利克雷原理”,这一原理在解决实际问题中有着广泛的应用。
(1)把5本书放进4个抽屉里,不管怎么放总有一个抽屉里至少有( )本书。
小练习
(2)7只鸽子飞回6个鸽舍,至少有2只鸽子要飞进同一个鸽舍里,为什么?
在有些问题中,“铅笔”和“杯子”不是很明显, 需要我们制造出“铅笔”和“杯子”
三个
性别
(3)三个朋友同行,其中必有两个小朋友性别相同。
小朋友
(4)一盒围棋棋子,黑白子混放,我们任意摸出3个棋子,至少有2个棋子是同颜色的,为什么?
黑色、白色相当于杯子或者抽屉
3个棋子就相当于是3枝铅笔或者3本书
(5) 任意13人中,总有至少几个人的属相相同,想一想,为什么?
提示:属相只有12个,13个人中即便12个人都是不同的属相,最后一个人的属相必然与其中一个人属相相同。因此,总有至少2个人的属相相同。
(6)一副扑克牌取出大小王,还剩52张牌,5个人每人随意抽一张,总有2张牌的花色相同,为什么?
讨论
5只鸽子飞进了3个鸽笼,总有一个鸽笼至少飞进了2只鸽子,为什么?
(1)把9个苹果放进6个抽屉里,总有一个抽屉至少有( )个苹果。
(2)把11只鸽子放进7个鸽巢,总有一个鸽巢至少有( )个鸽子。
练习2
2
2
世界级难题的简化版:
在1,2,3,……,10这10个自然数中,任意取出6个数,其中一定有两个互质数。
在1,2,3,4,5,6……,2n这2n个自然数中,任意取出n+1个数,其中一定有两个互质数。
试一试,你能行!
思考题:在1,2,3,……,2n这2n个自然数中,任意取出n+1
个数,其中一定有两个互质数。
提示:将相邻两个数作为一组,2n个数就有n组数,可以在n组数中任意取其中一个数,就取得了n个数,第n+1个数可以从n组数中任意一组中取出,此时,在这取出的数中,必然有两个数是相邻的数,而相邻的两个数就是互质数。
你有哪些收获?
再见
