2021—2022学年冀教版数学七年级下册第九章三角形单元检测(Word版含答案)
文档属性
| 名称 | 2021—2022学年冀教版数学七年级下册第九章三角形单元检测(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 388.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-21 07:56:54 | ||
图片预览



文档简介
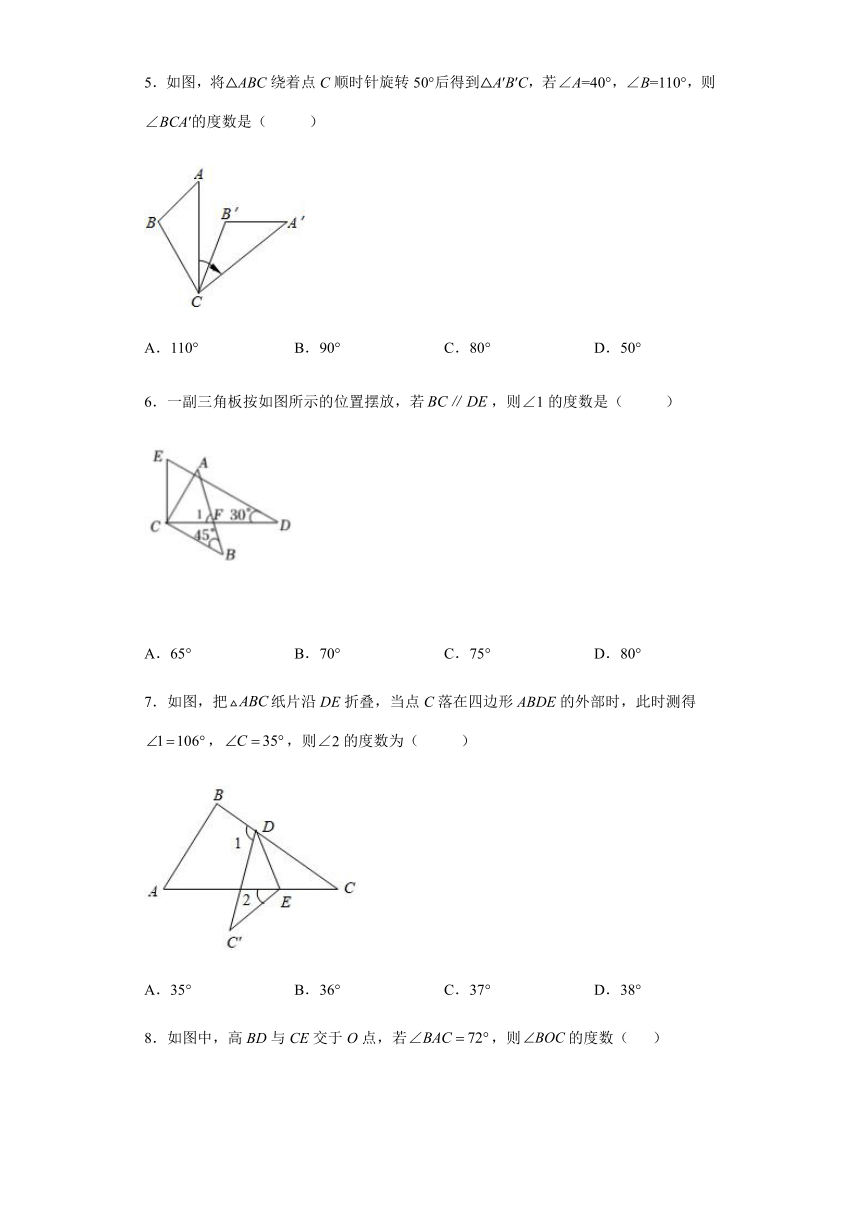
三角形单元检测
一、单选题
1.下列长度(单位:cm)的三条线段,能组成三角形的是( )
A.2,3,5 B.2,5,8 C.5,5,2 D.5,5,10
2.如图,ABC中,AB=15,BC=9,BD是AC边上的中线.若ABD的周长为35,则BCD的周长是( )
A.20 B.24 C.26 D.29
3.已知,图中的虚线部分是小玉作的辅助线,则下列结论正确的是( )
A.CD是边AB上的高 B.CD是边AC上的高
C.BD是边CB上的高 D.BD是边AC上的高
4.下列图形中,不具有稳定性的是( )
A. B.
C. D.
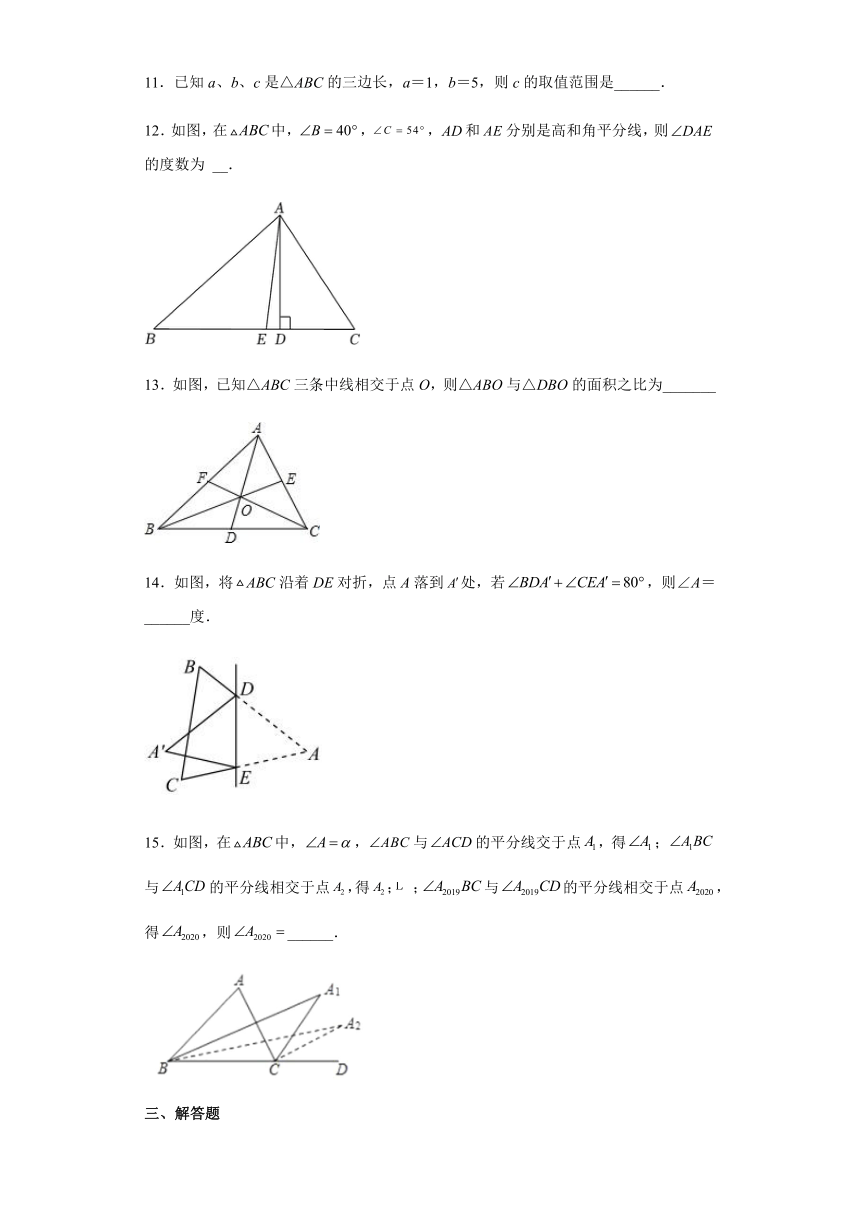
5.如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C,若∠A=40°,∠B=110°,则∠BCA′的度数是( )
A.110° B.90° C.80° D.50°
6.一副三角板按如图所示的位置摆放,若,则∠1的度数是( )
A.65° B.70° C.75° D.80°
7.如图,把纸片沿DE折叠,当点C落在四边形ABDE的外部时,此时测得,,则∠2的度数为( )
A.35° B.36° C.37° D.38°
8.如图中,高BD与CE交于O点,若,则的度数( )
A. B. C. D.
9.悬臂在生活中应用广泛,图1是一款利用悬臂原理设计的手机支架,图2为其平面示意图,若底座于点O,,则,,的数量关系是( )
A. B.
C. D.
10.如图,,将一副直角三角板作如下摆放,,.下列结论:①;②;③;④.其中正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题
11.已知a、b、c是△ABC的三边长,a=1,b=5,则c的取值范围是______.
12.如图,在中,,,和分别是高和角平分线,则的度数为 __.
13.如图,已知△ABC三条中线相交于点O,则△ABO与△DBO的面积之比为_______
14.如图,将ABC沿着DE对折,点A落到处,若,则∠A=______度.
15.如图,在中,,与的平分线交于点,得;与的平分线相交于点,得;;与的平分线相交于点,得,则______.
三、解答题
16.根据下列所给条件,判断的形状.
(1),,;
(2);
(3);
(4),.
17.已知三角形ABC的三边为a,b,c;
(1)若a=2,b=7,c为最长边且为整数,求三角形ABC的周长;
(2)化简:|a+b﹣c|﹣|b﹣a﹣c|+|a+b+c|.
18.如图所示,在中,,平分∠ACB,DE∥AC.
(1)求的度数;
(2)求的度数
19.如图,的角平分线、相交于点.
(1)若,,求的度数;
(2)求证:.
20.阅读填空,将三角尺(△MPN,∠MPN=90°)放置在△ABC上(点P在△ABC内),如图①所示,三角尺的两边PM、PN恰好经过点B和点C,我们来研究∠ABP与∠ACP是否存在某种数量关系.
(1)特例探索:
若∠A=50°,则∠PBC+∠PCB= 度,∠ABP+∠ACP= 度.
(2)类比探索:
∠ABP、∠ACP、∠A的关系是 .
(3)变式探索:
如图②所示,改变三角尺的位置,使点P在△ABC外,三角尺的两边PM、PN仍恰好经过点B和点C,则∠ABP、∠ACP、∠A的关系是 .
试卷第1页,共3页
答案
1.C
2.D
3.A
4.B
5.C
6.C
7.B
8.C
9.B
10.D
11.
12.7°
13.2:1
14.40
16.(1)通过最大角小于90°所以此三角形为锐角三角形;
(2)通过最大角大于90°所以此三角形为钝角三角形;
(3)通过最大角等于90°所以此三角形为直角三角形;
(4)通过三角形中有两条边相等可知此三角形为等腰三角形.
17.解:(1)∵a=2,b=7,
∴7﹣2<c<7+2,
即5<c<9,
∵c为最长边且为整数,
∴c=8,
∴三角形ABC的周长=2+7+8=17;
(2)∵三角形ABC的三边为a,b,c,
∴a+b>c,b<a+c,
∴a+b﹣c>0,b﹣a﹣c<0,a+b+c>0,
∴|a+b﹣c|﹣|b﹣a﹣c|+|a+b+c|=a+b﹣c+b﹣a﹣c+a+b+c=a+3b﹣c.
18.(1)在中,,
∴,
∵,
∴.
(2)平分,
∴,
∴
19.(1)解:,,
,
的角平分线 相交于点 ,
,,
,
(2)证明: 的角平分线 相交于点 ,,
即
20.(1)在中
∵∠MPN=90°
∴∠PBC+∠PCB=180°-∠MPN=180°-90°=90°
在中
∵∠A+∠ABC+∠ACB=180°
又∵∠ABC=∠PBC+∠ABP,∠ACB=∠ACP+∠BCP
∴∠A+∠PBC+∠ABP +∠ACP+∠BCP =180°
∵∠PBC+∠PCB=90°,∠A=50°
∴∠ABP +∠ACP=180°-90°-50°=40°
(2)由(1)问可知∠A+∠PBC+∠ABP +∠ACP+∠BCP =180°
又∵∠PBC+∠PCB=90°
∴∠A+∠ABP +∠ACP=180°-(∠PBC+∠PCB)=180°-90°=90°
(3)如图所示,设PN与AB交于点H
∵∠A+∠ACP=∠AHP
又∵∠ABP+∠MPN =∠AHP
∴∠A+∠ACP=∠ABP+∠MPN
又∵∠MPN =90°
∴∠A+∠ACP =90°+∠ABP
∴∠A+∠ACP-∠ABP=90°.
答案第1页,共2页
一、单选题
1.下列长度(单位:cm)的三条线段,能组成三角形的是( )
A.2,3,5 B.2,5,8 C.5,5,2 D.5,5,10
2.如图,ABC中,AB=15,BC=9,BD是AC边上的中线.若ABD的周长为35,则BCD的周长是( )
A.20 B.24 C.26 D.29
3.已知,图中的虚线部分是小玉作的辅助线,则下列结论正确的是( )
A.CD是边AB上的高 B.CD是边AC上的高
C.BD是边CB上的高 D.BD是边AC上的高
4.下列图形中,不具有稳定性的是( )
A. B.
C. D.
5.如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C,若∠A=40°,∠B=110°,则∠BCA′的度数是( )
A.110° B.90° C.80° D.50°
6.一副三角板按如图所示的位置摆放,若,则∠1的度数是( )
A.65° B.70° C.75° D.80°
7.如图,把纸片沿DE折叠,当点C落在四边形ABDE的外部时,此时测得,,则∠2的度数为( )
A.35° B.36° C.37° D.38°
8.如图中,高BD与CE交于O点,若,则的度数( )
A. B. C. D.
9.悬臂在生活中应用广泛,图1是一款利用悬臂原理设计的手机支架,图2为其平面示意图,若底座于点O,,则,,的数量关系是( )
A. B.
C. D.
10.如图,,将一副直角三角板作如下摆放,,.下列结论:①;②;③;④.其中正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题
11.已知a、b、c是△ABC的三边长,a=1,b=5,则c的取值范围是______.
12.如图,在中,,,和分别是高和角平分线,则的度数为 __.
13.如图,已知△ABC三条中线相交于点O,则△ABO与△DBO的面积之比为_______
14.如图,将ABC沿着DE对折,点A落到处,若,则∠A=______度.
15.如图,在中,,与的平分线交于点,得;与的平分线相交于点,得;;与的平分线相交于点,得,则______.
三、解答题
16.根据下列所给条件,判断的形状.
(1),,;
(2);
(3);
(4),.
17.已知三角形ABC的三边为a,b,c;
(1)若a=2,b=7,c为最长边且为整数,求三角形ABC的周长;
(2)化简:|a+b﹣c|﹣|b﹣a﹣c|+|a+b+c|.
18.如图所示,在中,,平分∠ACB,DE∥AC.
(1)求的度数;
(2)求的度数
19.如图,的角平分线、相交于点.
(1)若,,求的度数;
(2)求证:.
20.阅读填空,将三角尺(△MPN,∠MPN=90°)放置在△ABC上(点P在△ABC内),如图①所示,三角尺的两边PM、PN恰好经过点B和点C,我们来研究∠ABP与∠ACP是否存在某种数量关系.
(1)特例探索:
若∠A=50°,则∠PBC+∠PCB= 度,∠ABP+∠ACP= 度.
(2)类比探索:
∠ABP、∠ACP、∠A的关系是 .
(3)变式探索:
如图②所示,改变三角尺的位置,使点P在△ABC外,三角尺的两边PM、PN仍恰好经过点B和点C,则∠ABP、∠ACP、∠A的关系是 .
试卷第1页,共3页
答案
1.C
2.D
3.A
4.B
5.C
6.C
7.B
8.C
9.B
10.D
11.
12.7°
13.2:1
14.40
16.(1)通过最大角小于90°所以此三角形为锐角三角形;
(2)通过最大角大于90°所以此三角形为钝角三角形;
(3)通过最大角等于90°所以此三角形为直角三角形;
(4)通过三角形中有两条边相等可知此三角形为等腰三角形.
17.解:(1)∵a=2,b=7,
∴7﹣2<c<7+2,
即5<c<9,
∵c为最长边且为整数,
∴c=8,
∴三角形ABC的周长=2+7+8=17;
(2)∵三角形ABC的三边为a,b,c,
∴a+b>c,b<a+c,
∴a+b﹣c>0,b﹣a﹣c<0,a+b+c>0,
∴|a+b﹣c|﹣|b﹣a﹣c|+|a+b+c|=a+b﹣c+b﹣a﹣c+a+b+c=a+3b﹣c.
18.(1)在中,,
∴,
∵,
∴.
(2)平分,
∴,
∴
19.(1)解:,,
,
的角平分线 相交于点 ,
,,
,
(2)证明: 的角平分线 相交于点 ,,
即
20.(1)在中
∵∠MPN=90°
∴∠PBC+∠PCB=180°-∠MPN=180°-90°=90°
在中
∵∠A+∠ABC+∠ACB=180°
又∵∠ABC=∠PBC+∠ABP,∠ACB=∠ACP+∠BCP
∴∠A+∠PBC+∠ABP +∠ACP+∠BCP =180°
∵∠PBC+∠PCB=90°,∠A=50°
∴∠ABP +∠ACP=180°-90°-50°=40°
(2)由(1)问可知∠A+∠PBC+∠ABP +∠ACP+∠BCP =180°
又∵∠PBC+∠PCB=90°
∴∠A+∠ABP +∠ACP=180°-(∠PBC+∠PCB)=180°-90°=90°
(3)如图所示,设PN与AB交于点H
∵∠A+∠ACP=∠AHP
又∵∠ABP+∠MPN =∠AHP
∴∠A+∠ACP=∠ABP+∠MPN
又∵∠MPN =90°
∴∠A+∠ACP =90°+∠ABP
∴∠A+∠ACP-∠ABP=90°.
答案第1页,共2页
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
