高中数学苏教版(2019)选择性必修第二册第6章 空间向量与立体几何 章末检测试卷 (word版含解析)
文档属性
| 名称 | 高中数学苏教版(2019)选择性必修第二册第6章 空间向量与立体几何 章末检测试卷 (word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 436.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-21 10:58:14 | ||
图片预览



文档简介
第6章 空间向量与立体几何 章末检测试卷
(时间:120分钟 满分:150分)
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.在长方体ABCD-A1B1C1D1中,++-等于( )
A. B.
C. D.
2.已知a=(2,-1,3),b=(-1,4,-2),c=(1,3,λ),若a,b,c三向量共面,则实数λ等于( )
A.1 B.2 C.3 D.4
3.已知平面α上的两个向量a=(2,3,1),b=(5,6,4),则平面α的一个法向量为( )
A.(1,-1,1) B.(2,-1,1)
C.(-2,1,1) D.(-1,1,1)
4.A,B,C,D是空间不共面的四点,且满足·=0,·=0,·=0,M为BC中点,则△AMD的形状为( )
A.等腰三角形 B.锐角三角形
C.直角三角形 D.钝角三角形
5.已知空间向量a=(1,n,2),b=(-2,1,2),若2a-b与b垂直,则|a|等于( )
A. B. C. D.
6.如图,在正方体ABCD-A1B1C1D1中,以D为原点建立空间直角坐标系,E为BB1的中点,F为A1D1的中点,则下列向量中,能作为平面AEF的法向量的是( )
A.(1,-2,4) B.(-4,1,-2)
C.(2,-2,1) D.(1,2,-2)
7.如图,AB=AC=BD=1,AB 平面α,AC⊥平面α,BD⊥AB,BD与平面α成30°角,则C,D间的距离为( )
A.1 B.2 C. D.
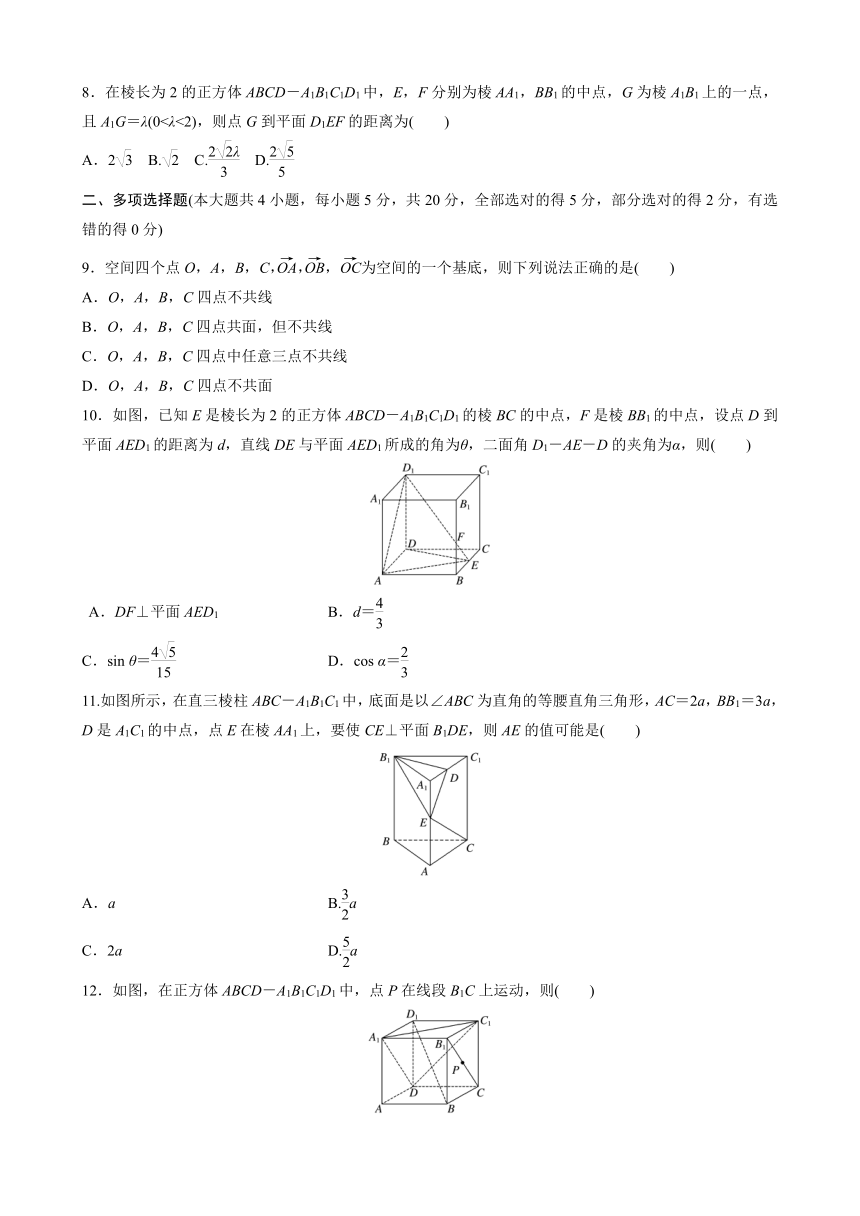
8.在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为棱AA1,BB1的中点,G为棱A1B1上的一点,且A1G=λ(0<λ<2),则点G到平面D1EF的距离为( )
A.2 B. C. D.
二、多项选择题(本大题共4小题,每小题5分,共20分,全部选对的得5分,部分选对的得2分,有选错的得0分)
9.空间四个点O,A,B,C,,,为空间的一个基底,则下列说法正确的是( )
A.O,A,B,C四点不共线
B.O,A,B,C四点共面,但不共线
C.O,A,B,C四点中任意三点不共线
D.O,A,B,C四点不共面
10.如图,已知E是棱长为2的正方体ABCD-A1B1C1D1的棱BC的中点,F是棱BB1的中点,设点D到平面AED1的距离为d,直线DE与平面AED1所成的角为θ,二面角D1-AE-D的夹角为α,则( )
A.DF⊥平面AED1 B.d=
C.sin θ= D.cos α=
11.如图所示,在直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D是A1C1的中点,点E在棱AA1上,要使CE⊥平面B1DE,则AE的值可能是( )
A.a B.a
C.2a D.a
12.如图,在正方体ABCD-A1B1C1D1中,点P在线段B1C上运动,则( )
A.直线BD1⊥平面A1C1D
B.三棱锥P-A1C1D的体积为定值
C.异面直线AP与A1D所成的角的取值范围是
D.直线C1P与平面A1C1D所成角的正弦值的最大值为
三、填空题(本大题共4小题,每小题5分,共20分)
13.已知点B(1,0,0),C′(1,1,1),D′(0,1,1),若点E的坐标为(-2,1,m),且点B,C′,D′,E四点共面,则实数m的值为________.
14.已知平面α经过点B(1,0,0),且α的法向量n=(1,1,1),则P(2,2,0)到平面α的距离为________.
15.已知在正四棱台ABCD-A1B1C1D1中,上底面A1B1C1D1的边长为1,下底面ABCD的边长为2,侧棱与底面所成的角为60°,则异面直线AD1与B1C所成的角的余弦值为________.
16.如图,有一长方形的纸片ABCD,AB的长度为4 cm,BC的长度为3 cm,现沿它的一条对角线AC把它折叠成90°的二面角,则折叠后·=________,线段BD的长是________cm.
四、解答题(本大题共6小题,共70分)
17.(10分)如图所示,在四棱锥M-ABCD中,底面ABCD是边长为2的正方形,侧棱AM的长为3,且AM和AB,AD的夹角都是60°,N是CM的中点,设a=,b=,c=,试以a,b,c为基向量表示出向量,并求BN的长.
.
18.(12分)已知空间内三点A(0,2,3),B(-2,1,6),C(1,-1,5).
(1)求以向量,为一组邻边的平行四边形的面积S;
(2)若向量a与向量,都垂直,且|a|=,求向量a的坐标.
19.(12分)如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E,F分别是AB,PB的中点.
(1)求证:EF⊥CD;
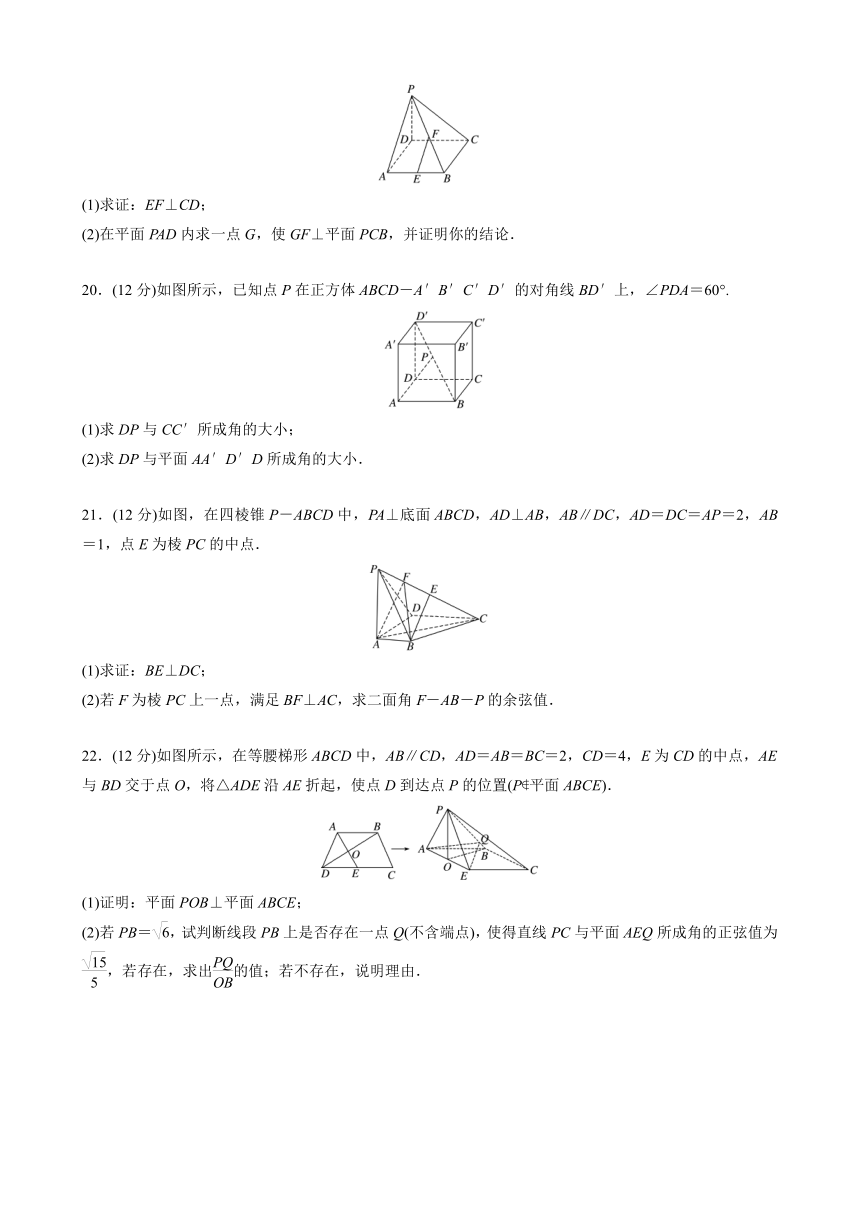
(2)在平面PAD内求一点G,使GF⊥平面PCB,并证明你的结论.
20.(12分)如图所示,已知点P在正方体ABCD-A′B′C′D′的对角线BD′上,∠PDA=60°.
(1)求DP与CC′所成角的大小;
(2)求DP与平面AA′D′D所成角的大小.
21.(12分)如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.
(1)求证:BE⊥DC;
(2)若F为棱PC上一点,满足BF⊥AC,求二面角F-AB-P的余弦值.
22.(12分)如图所示,在等腰梯形ABCD中,AB∥CD,AD=AB=BC=2,CD=4,E为CD的中点,AE与BD交于点O,将△ADE沿AE折起,使点D到达点P的位置(P 平面ABCE).
(1)证明:平面POB⊥平面ABCE;
(2)若PB=,试判断线段PB上是否存在一点Q(不含端点),使得直线PC与平面AEQ所成角的正弦值为,若存在,求出的值;若不存在,说明理由.
答案与解析
第6章 空间向量与立体几何 章末检测试卷
(时间:120分钟 满分:150分)
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.在长方体ABCD-A1B1C1D1中,++-等于( )
A. B.
C. D.
答案 A
解析 ++-=+=.
2.已知a=(2,-1,3),b=(-1,4,-2),c=(1,3,λ),若a,b,c三向量共面,则实数λ等于( )
A.1 B.2 C.3 D.4
答案 A
解析 若向量a,b,c共面,则c=xa+yb,其中x,y∈R,
即(1,3,λ)=(2x,-x,3x)+(-y,4y,-2y)=(2x-y,-x+4y,3x-2y),
则解得
3.已知平面α上的两个向量a=(2,3,1),b=(5,6,4),则平面α的一个法向量为( )
A.(1,-1,1) B.(2,-1,1)
C.(-2,1,1) D.(-1,1,1)
答案 C
解析 显然a与b不平行,
设平面α的法向量为n=(x,y,z),
则所以
令z=1,得x=-2,y=1.
所以n=(-2,1,1).
4.A,B,C,D是空间不共面的四点,且满足·=0,·=0,·=0,M为BC中点,则△AMD的形状为( )
A.等腰三角形 B.锐角三角形
C.直角三角形 D.钝角三角形
答案 C
解析 ∵M为BC中点,∴=(+).
∴·=(+)·
=·+·=0.
∴AM⊥AD,△AMD为直角三角形.
5.已知空间向量a=(1,n,2),b=(-2,1,2),若2a-b与b垂直,则|a|等于( )
A. B. C. D.
答案 B
解析 因为a=(1,n,2),b=(-2,1,2),
所以2a-b=(4,2n-1,2).
因为2a-b与b垂直,
所以(2a-b)·b=0,所以-8+2n-1+4=0,
解得n=,所以a=,
所以|a|==.
6.如图,在正方体ABCD-A1B1C1D1中,以D为原点建立空间直角坐标系,E为BB1的中点,F为A1D1的中点,则下列向量中,能作为平面AEF的法向量的是( )
A.(1,-2,4) B.(-4,1,-2)
C.(2,-2,1) D.(1,2,-2)
答案 B
解析 设正方体的棱长为2,
则A(2,0,0),E(2,2,1),F(1,0,2),
所以=(0,2,1),=(-1,0,2).
设向量n=(x,y,z)是平面AEF的法向量,
则取y=1,得x=-4,z=-2,
则n=(-4,1,-2)是平面AEF的一个法向量.结合其他选项,检验可知只有B选项是平面AEF的法向量.
7.如图,AB=AC=BD=1,AB 平面α,AC⊥平面α,BD⊥AB,BD与平面α成30°角,则C,D间的距离为( )
A.1 B.2 C. D.
答案 C
解析 ||2=|++|2=||2+||2+||2+2·+2·+2·=1+1+1+0+0+2×1×1·cos 120°=2.
∴||=.
8.在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为棱AA1,BB1的中点,G为棱A1B1上的一点,且A1G=λ(0<λ<2),则点G到平面D1EF的距离为( )
A.2 B. C. D.
答案 D
解析 以D为坐标原点,DA所在直线为x轴,DC所在直线为y轴,DD1所在直线为z轴,建立如图所示的空间直角坐标系,
则G(2,λ,2),D1(0,0,2),E(2,0,1),F(2,2,1),
所以=(-2,0,1),=(0,2,0),=(0,λ,1).
设平面D1EF的法向量为n=(x,y,z),
则
取x=1,得n=(1,0,2)为平面D1EF的一个法向量,
∴点G到平面D1EF的距离为
d===.
二、多项选择题(本大题共4小题,每小题5分,共20分,全部选对的得5分,部分选对的得2分,有选错的得0分)
9.空间四个点O,A,B,C,,,为空间的一个基底,则下列说法正确的是( )
A.O,A,B,C四点不共线
B.O,A,B,C四点共面,但不共线
C.O,A,B,C四点中任意三点不共线
D.O,A,B,C四点不共面
答案 ACD
解析 若O,A,B,C四点共面,则,,共面,则,,不可能为空间的一个基底,故A,D正确,B不正确;若O,A,B,C中有三点共线,则四点一定共面,故C正确.
10.如图,已知E是棱长为2的正方体ABCD-A1B1C1D1的棱BC的中点,F是棱BB1的中点,设点D到平面AED1的距离为d,直线DE与平面AED1所成的角为θ,二面角D1-AE-D的夹角为α,则( )
A.DF⊥平面AED1 B.d=
C.sin θ= D.cos α=
答案 BCD
解析 以A为坐标原点,,,的方向为x,y,z轴的正方向,建立空间直角坐标系(图略),
则A(0,0,0),E(2,1,0),D(0,2,0),D1(0,2,2),
A1(0,0,2),F(2,0,1),
所以=(2,1,0),=(0,2,2),=(2,-1,0),=(2,-2,1).
设平面AED1的法向量为m=(x,y,z),
则由
得
令x=1,则y=-2,z=2,
故m=(1,-2,2).
∵=(2,-2,1),不存在λ使m=λ,
即与m不共线,
∴DF与平面AED1不垂直,故A错误;
又∵=(0,0,2),
∴d===,故B正确;
又=(2,-1,0).
∴sin θ=|cos〈,m〉|==.
故C正确;
又=(0,0,2)为平面AED的一个法向量,
由图知α为锐角,
∴cos α===,故D正确.
11.如图所示,在直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D是A1C1的中点,点E在棱AA1上,要使CE⊥平面B1DE,则AE的值可能是( )
A.a B.a
C.2a D.a
答案 AC
解析 以B为坐标原点,BA,BC,BB1所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系,
则D,
B1(0,0,3a),C(0,a,0).
设点E的坐标为(a,0,z)(0≤z≤3a),
则=,
=(a,-a,z),=(a,0,z-3a).
由CE⊥平面B1DE,得CE⊥DE,CE⊥B1E,
故
即
解得z=a或z=2a,即AE=a或2a.
12.如图,在正方体ABCD-A1B1C1D1中,点P在线段B1C上运动,则( )
A.直线BD1⊥平面A1C1D
B.三棱锥P-A1C1D的体积为定值
C.异面直线AP与A1D所成的角的取值范围是
D.直线C1P与平面A1C1D所成角的正弦值的最大值为
答案 ABD
解析 对于选项A,连接B1D1(图略),由正方体可得A1C1⊥B1D1,且BB1⊥平面A1B1C1D1,
则BB1⊥A1C1,所以A1C1⊥平面BD1B1,
故A1C1⊥BD1;
同理,连接AD1,易证得A1D⊥BD1,
则BD1⊥平面A1C1D,故A正确;
对于选项B,
因为点P在线段B1C上运动,
所以=A1D·AB,面积为定值,
且C1到平面A1PD的距离即为C1到平面A1B1CD的距离,也为定值,故体积为定值,故B正确;
对于选项C,当点P与线段B1C的端点重合时,AP与A1D所成的角取得最小值为60°,故C错误;
对于选项D,因为直线BD1⊥平面A1C1D,
所以若直线C1P与平面A1C1D所成角的正弦值最大,
则直线C1P与直线BD1所成的角的余弦值最大,
则P运动到B1C中点处,即所成的角为∠C1BD1,
设棱长为1,在Rt△D1C1B中,cos∠C1BD1===,故D正确.
三、填空题(本大题共4小题,每小题5分,共20分)
13.已知点B(1,0,0),C′(1,1,1),D′(0,1,1),若点E的坐标为(-2,1,m),且点B,C′,D′,E四点共面,则实数m的值为________.
答案 1
解析 ∵B(1,0,0),C′(1,1,1),D′(0,1,1),E(-2,1,m),
∴=(0,1,1),=(-1,1,1),=(-3,1,m),
根据空间向量基本定理,存在实数x,y,
使得=x+y,
则有
解得m=1.
14.已知平面α经过点B(1,0,0),且α的法向量n=(1,1,1),则P(2,2,0)到平面α的距离为________.
答案
解析 ∵向量n=(1,1,1)为平面α的法向量,点B(1,0,0),P(2,2,0),
∴=(1,2,0),
∴P(2,2,0)到平面α的距离d===.
15.已知在正四棱台ABCD-A1B1C1D1中,上底面A1B1C1D1的边长为1,下底面ABCD的边长为2,侧棱与底面所成的角为60°,则异面直线AD1与B1C所成的角的余弦值为________.
答案
解析 设上、下底面中心分别为O1,O,则OO1⊥平面ABCD,以O为原点,直线BD,AC,OO1分别为x轴,y轴,z轴建立空间直角坐标系.
因为AB=2,A1B1=1,
所以AC=BD=2,A1C1=B1D1=.
因为平面BDD1B1⊥平面ABCD,
所以∠B1BO为侧棱与底面所成的角,故∠B1BO=60°.
设棱台高为h,则tan 60°=,h=,
所以A(0,-,0),D1,B1,
C(0,,0),
所以=,
=,
故cos〈,〉==,
故异面直线AD1与B1C所成的角的余弦值为.
16.如图,有一长方形的纸片ABCD,AB的长度为4 cm,BC的长度为3 cm,现沿它的一条对角线AC把它折叠成90°的二面角,则折叠后·=________,线段BD的长是________cm.
答案 -7
解析 如图所示,
作DE⊥AC,BF⊥AC,
垂足分别为E,F,
则AC=5,DE=BF=,
AE=CF=,EF=,
折叠后,DE,EF,FB的长度保持不变,
所以·=·(+)=·+·=5×4×+5×3×=-7,
故||2=(++)2
=||2+||2+||2+2·+2·+2·
=||2+||2+||2+0+0+0
=2+2+2=,
得BD=.
四、解答题(本大题共6小题,共70分)
17.(10分)如图所示,在四棱锥M-ABCD中,底面ABCD是边长为2的正方形,侧棱AM的长为3,且AM和AB,AD的夹角都是60°,N是CM的中点,设a=,b=,c=,试以a,b,c为基向量表示出向量,并求BN的长.
解 =+=+
=+(-)
=+[-(+)]
=-++.
所以=-a+b+c,
||2=2=2
=(a2+b2+c2-2a·b-2a·c+2b·c)=.
所以||=,即BN的长为.
18.(12分)已知空间内三点A(0,2,3),B(-2,1,6),C(1,-1,5).
(1)求以向量,为一组邻边的平行四边形的面积S;
(2)若向量a与向量,都垂直,且|a|=,求向量a的坐标.
解 (1)∵=(-2,-1,3),=(1,-3,2),
∴cos∠BAC===,
又∵∠BAC∈[0,π],
∴∠BAC=,
∴S=||||sin =7.
(2)设a=(x,y,z),
由a⊥,得-2x-y+3z=0,
由a⊥,得x-3y+2z=0,
由|a|=,得x2+y2+z2=3,
∴x=y=z=1或x=y=z=-1.
∴a=(1,1,1)或a=(-1,-1,-1).
19.(12分)如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E,F分别是AB,PB的中点.
(1)求证:EF⊥CD;
(2)在平面PAD内求一点G,使GF⊥平面PCB,并证明你的结论.
(1)证明 如图,以D为原点,分别以DA,DC,DP所在直线为x轴,y轴,z轴建立空间直角坐标系,
设AD=a,则D(0,0,0),
A(a,0,0),B(a,a,0),C(0,a,0),
E,P(0,0,a),
F.
=,=(0,a,0),
∵·=0,∴⊥,即EF⊥CD.
(2)解 设G(x,0,z),则=,
若使GF⊥平面PCB,则需·=0且·=0,
由·=·(a,0,0)
=a=0,得x=,
由·=·(0,-a,a)
=+a=0,
得z=0.
∴G点坐标为,即G为AD的中点时,GF⊥平面PCB.
20.(12分)如图所示,已知点P在正方体ABCD-A′B′C′D′的对角线BD′上,∠PDA=60°.
(1)求DP与CC′所成角的大小;
(2)求DP与平面AA′D′D所成角的大小.
解 (1)如图所示,以D为原点,DA,DC,DD′分别为x轴,y轴,z轴正方向建立空间直角坐标系,设DA=1.
则=(1,0,0),=(0,0,1).
连接BD,B′D′.
在平面BB′D′D中,延长DP交B′D′于H.
设=(m,m,1)(m>0),
由已知得〈·〉=60°,
由·=||||cos〈,〉,
可得2m=.
解得m=,
所以=.
因为cos〈,〉==,
所以〈,〉=45°,
即DP与CC′所成的角为45°.
(2)由题意得,平面AA′D′D的一个法向量是
=(0,1,0),
因为cos〈,〉
==,
所以〈,〉=60°,
可得DP与平面AA′D′D所成的角为30°.
21.(12分)如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.
(1)求证:BE⊥DC;
(2)若F为棱PC上一点,满足BF⊥AC,求二面角F-AB-P的余弦值.
(1)证明 依题意,以点A为坐标原点建立空间直角坐标系(如图),可得A(0,0,0),
B(1,0,0),C(2,2,0),D(0,2,0),
P(0,0,2).
由E为棱PC的中点,得E(1,1,1),
所以=(0,1,1),=(2,0,0),
故·=0,
所以BE⊥DC.
(2)解 =(1,2,0),=(-2,-2,2),=(2,2,0),=(1,0,0).
由点F在棱PC上,设=λ(0≤λ≤1),
故=+=+λ=(1-2λ,2-2λ,2λ).
由BF⊥AC,得·=0,
则2(1-2λ)+2(2-2λ)=0,解得λ=,
即=.
设n1=(x,y,z)为平面FAB的法向量,
则
即
不妨令z=1,可得n1=(0,-3,1)为平面FAB的一个法向量.
易知向量n2=(0,1,0)为平面ABP的一个法向量,
则cos〈n1,n2〉===-.
由图可知,二面角F-AB-P为锐角,
所以二面角F-AB-P的余弦值为.
22.(12分)如图所示,在等腰梯形ABCD中,AB∥CD,AD=AB=BC=2,CD=4,E为CD的中点,AE与BD交于点O,将△ADE沿AE折起,使点D到达点P的位置(P 平面ABCE).
(1)证明:平面POB⊥平面ABCE;
(2)若PB=,试判断线段PB上是否存在一点Q(不含端点),使得直线PC与平面AEQ所成角的正弦值为,若存在,求出的值;若不存在,说明理由.
(1)证明 在梯形ABCD中,连接BE(图略),
∵AD=AB=BC=2,CD=4,E为中点,
∴四边形ABED为菱形,∴BD⊥AE,
∴OB⊥AE,OD⊥AE,
即OB⊥AE,OP⊥AE,且OB∩OP=O,
OB 平面POB,OP 平面POB,
∴AE⊥平面POB.
又AE 平面ABCE,∴平面POB⊥平面ABCE.
(2)由(1)可知四边形ABED为菱形,
∴AD=DE=2,
在等腰梯形ABCD中,AE=BC=2,
∴△PAE为正三角形,∴OP=,同理OB=,
∵PB=,∴OP2+OB2=PB2,∴OP⊥OB.
由(1)可知OP⊥AE,OB⊥AE,
以O为原点,,,分别为x轴,y轴,z轴,建立空间直角坐标系O-xyz,
则P(0,0,),A(-1,0,0),B(0,,0),C(2,,0),
E(1,0,0),
∴=(1,0,),=(0,,-),
=(2,,-),=(2,0,0),
设=λ(0<λ<1),
=+=+λ=(1,λ,-λ),
设平面AEQ的一个法向量为n=(x,y,z),
则即
取x=0,y=1,得z=,
∴n=,
设直线PC与平面AEQ所成角为θ,θ∈,
则sin θ=|cos〈,n〉|==,
即=,
化简得4λ2-4λ+1=0,解得λ=,
∴存在点Q为PB的中点时,使直线PC与平面AEQ所成角的正弦值为.
(时间:120分钟 满分:150分)
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.在长方体ABCD-A1B1C1D1中,++-等于( )
A. B.
C. D.
2.已知a=(2,-1,3),b=(-1,4,-2),c=(1,3,λ),若a,b,c三向量共面,则实数λ等于( )
A.1 B.2 C.3 D.4
3.已知平面α上的两个向量a=(2,3,1),b=(5,6,4),则平面α的一个法向量为( )
A.(1,-1,1) B.(2,-1,1)
C.(-2,1,1) D.(-1,1,1)
4.A,B,C,D是空间不共面的四点,且满足·=0,·=0,·=0,M为BC中点,则△AMD的形状为( )
A.等腰三角形 B.锐角三角形
C.直角三角形 D.钝角三角形
5.已知空间向量a=(1,n,2),b=(-2,1,2),若2a-b与b垂直,则|a|等于( )
A. B. C. D.
6.如图,在正方体ABCD-A1B1C1D1中,以D为原点建立空间直角坐标系,E为BB1的中点,F为A1D1的中点,则下列向量中,能作为平面AEF的法向量的是( )
A.(1,-2,4) B.(-4,1,-2)
C.(2,-2,1) D.(1,2,-2)
7.如图,AB=AC=BD=1,AB 平面α,AC⊥平面α,BD⊥AB,BD与平面α成30°角,则C,D间的距离为( )
A.1 B.2 C. D.
8.在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为棱AA1,BB1的中点,G为棱A1B1上的一点,且A1G=λ(0<λ<2),则点G到平面D1EF的距离为( )
A.2 B. C. D.
二、多项选择题(本大题共4小题,每小题5分,共20分,全部选对的得5分,部分选对的得2分,有选错的得0分)
9.空间四个点O,A,B,C,,,为空间的一个基底,则下列说法正确的是( )
A.O,A,B,C四点不共线
B.O,A,B,C四点共面,但不共线
C.O,A,B,C四点中任意三点不共线
D.O,A,B,C四点不共面
10.如图,已知E是棱长为2的正方体ABCD-A1B1C1D1的棱BC的中点,F是棱BB1的中点,设点D到平面AED1的距离为d,直线DE与平面AED1所成的角为θ,二面角D1-AE-D的夹角为α,则( )
A.DF⊥平面AED1 B.d=
C.sin θ= D.cos α=
11.如图所示,在直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D是A1C1的中点,点E在棱AA1上,要使CE⊥平面B1DE,则AE的值可能是( )
A.a B.a
C.2a D.a
12.如图,在正方体ABCD-A1B1C1D1中,点P在线段B1C上运动,则( )
A.直线BD1⊥平面A1C1D
B.三棱锥P-A1C1D的体积为定值
C.异面直线AP与A1D所成的角的取值范围是
D.直线C1P与平面A1C1D所成角的正弦值的最大值为
三、填空题(本大题共4小题,每小题5分,共20分)
13.已知点B(1,0,0),C′(1,1,1),D′(0,1,1),若点E的坐标为(-2,1,m),且点B,C′,D′,E四点共面,则实数m的值为________.
14.已知平面α经过点B(1,0,0),且α的法向量n=(1,1,1),则P(2,2,0)到平面α的距离为________.
15.已知在正四棱台ABCD-A1B1C1D1中,上底面A1B1C1D1的边长为1,下底面ABCD的边长为2,侧棱与底面所成的角为60°,则异面直线AD1与B1C所成的角的余弦值为________.
16.如图,有一长方形的纸片ABCD,AB的长度为4 cm,BC的长度为3 cm,现沿它的一条对角线AC把它折叠成90°的二面角,则折叠后·=________,线段BD的长是________cm.
四、解答题(本大题共6小题,共70分)
17.(10分)如图所示,在四棱锥M-ABCD中,底面ABCD是边长为2的正方形,侧棱AM的长为3,且AM和AB,AD的夹角都是60°,N是CM的中点,设a=,b=,c=,试以a,b,c为基向量表示出向量,并求BN的长.
.
18.(12分)已知空间内三点A(0,2,3),B(-2,1,6),C(1,-1,5).
(1)求以向量,为一组邻边的平行四边形的面积S;
(2)若向量a与向量,都垂直,且|a|=,求向量a的坐标.
19.(12分)如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E,F分别是AB,PB的中点.
(1)求证:EF⊥CD;
(2)在平面PAD内求一点G,使GF⊥平面PCB,并证明你的结论.
20.(12分)如图所示,已知点P在正方体ABCD-A′B′C′D′的对角线BD′上,∠PDA=60°.
(1)求DP与CC′所成角的大小;
(2)求DP与平面AA′D′D所成角的大小.
21.(12分)如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.
(1)求证:BE⊥DC;
(2)若F为棱PC上一点,满足BF⊥AC,求二面角F-AB-P的余弦值.
22.(12分)如图所示,在等腰梯形ABCD中,AB∥CD,AD=AB=BC=2,CD=4,E为CD的中点,AE与BD交于点O,将△ADE沿AE折起,使点D到达点P的位置(P 平面ABCE).
(1)证明:平面POB⊥平面ABCE;
(2)若PB=,试判断线段PB上是否存在一点Q(不含端点),使得直线PC与平面AEQ所成角的正弦值为,若存在,求出的值;若不存在,说明理由.
答案与解析
第6章 空间向量与立体几何 章末检测试卷
(时间:120分钟 满分:150分)
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.在长方体ABCD-A1B1C1D1中,++-等于( )
A. B.
C. D.
答案 A
解析 ++-=+=.
2.已知a=(2,-1,3),b=(-1,4,-2),c=(1,3,λ),若a,b,c三向量共面,则实数λ等于( )
A.1 B.2 C.3 D.4
答案 A
解析 若向量a,b,c共面,则c=xa+yb,其中x,y∈R,
即(1,3,λ)=(2x,-x,3x)+(-y,4y,-2y)=(2x-y,-x+4y,3x-2y),
则解得
3.已知平面α上的两个向量a=(2,3,1),b=(5,6,4),则平面α的一个法向量为( )
A.(1,-1,1) B.(2,-1,1)
C.(-2,1,1) D.(-1,1,1)
答案 C
解析 显然a与b不平行,
设平面α的法向量为n=(x,y,z),
则所以
令z=1,得x=-2,y=1.
所以n=(-2,1,1).
4.A,B,C,D是空间不共面的四点,且满足·=0,·=0,·=0,M为BC中点,则△AMD的形状为( )
A.等腰三角形 B.锐角三角形
C.直角三角形 D.钝角三角形
答案 C
解析 ∵M为BC中点,∴=(+).
∴·=(+)·
=·+·=0.
∴AM⊥AD,△AMD为直角三角形.
5.已知空间向量a=(1,n,2),b=(-2,1,2),若2a-b与b垂直,则|a|等于( )
A. B. C. D.
答案 B
解析 因为a=(1,n,2),b=(-2,1,2),
所以2a-b=(4,2n-1,2).
因为2a-b与b垂直,
所以(2a-b)·b=0,所以-8+2n-1+4=0,
解得n=,所以a=,
所以|a|==.
6.如图,在正方体ABCD-A1B1C1D1中,以D为原点建立空间直角坐标系,E为BB1的中点,F为A1D1的中点,则下列向量中,能作为平面AEF的法向量的是( )
A.(1,-2,4) B.(-4,1,-2)
C.(2,-2,1) D.(1,2,-2)
答案 B
解析 设正方体的棱长为2,
则A(2,0,0),E(2,2,1),F(1,0,2),
所以=(0,2,1),=(-1,0,2).
设向量n=(x,y,z)是平面AEF的法向量,
则取y=1,得x=-4,z=-2,
则n=(-4,1,-2)是平面AEF的一个法向量.结合其他选项,检验可知只有B选项是平面AEF的法向量.
7.如图,AB=AC=BD=1,AB 平面α,AC⊥平面α,BD⊥AB,BD与平面α成30°角,则C,D间的距离为( )
A.1 B.2 C. D.
答案 C
解析 ||2=|++|2=||2+||2+||2+2·+2·+2·=1+1+1+0+0+2×1×1·cos 120°=2.
∴||=.
8.在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为棱AA1,BB1的中点,G为棱A1B1上的一点,且A1G=λ(0<λ<2),则点G到平面D1EF的距离为( )
A.2 B. C. D.
答案 D
解析 以D为坐标原点,DA所在直线为x轴,DC所在直线为y轴,DD1所在直线为z轴,建立如图所示的空间直角坐标系,
则G(2,λ,2),D1(0,0,2),E(2,0,1),F(2,2,1),
所以=(-2,0,1),=(0,2,0),=(0,λ,1).
设平面D1EF的法向量为n=(x,y,z),
则
取x=1,得n=(1,0,2)为平面D1EF的一个法向量,
∴点G到平面D1EF的距离为
d===.
二、多项选择题(本大题共4小题,每小题5分,共20分,全部选对的得5分,部分选对的得2分,有选错的得0分)
9.空间四个点O,A,B,C,,,为空间的一个基底,则下列说法正确的是( )
A.O,A,B,C四点不共线
B.O,A,B,C四点共面,但不共线
C.O,A,B,C四点中任意三点不共线
D.O,A,B,C四点不共面
答案 ACD
解析 若O,A,B,C四点共面,则,,共面,则,,不可能为空间的一个基底,故A,D正确,B不正确;若O,A,B,C中有三点共线,则四点一定共面,故C正确.
10.如图,已知E是棱长为2的正方体ABCD-A1B1C1D1的棱BC的中点,F是棱BB1的中点,设点D到平面AED1的距离为d,直线DE与平面AED1所成的角为θ,二面角D1-AE-D的夹角为α,则( )
A.DF⊥平面AED1 B.d=
C.sin θ= D.cos α=
答案 BCD
解析 以A为坐标原点,,,的方向为x,y,z轴的正方向,建立空间直角坐标系(图略),
则A(0,0,0),E(2,1,0),D(0,2,0),D1(0,2,2),
A1(0,0,2),F(2,0,1),
所以=(2,1,0),=(0,2,2),=(2,-1,0),=(2,-2,1).
设平面AED1的法向量为m=(x,y,z),
则由
得
令x=1,则y=-2,z=2,
故m=(1,-2,2).
∵=(2,-2,1),不存在λ使m=λ,
即与m不共线,
∴DF与平面AED1不垂直,故A错误;
又∵=(0,0,2),
∴d===,故B正确;
又=(2,-1,0).
∴sin θ=|cos〈,m〉|==.
故C正确;
又=(0,0,2)为平面AED的一个法向量,
由图知α为锐角,
∴cos α===,故D正确.
11.如图所示,在直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D是A1C1的中点,点E在棱AA1上,要使CE⊥平面B1DE,则AE的值可能是( )
A.a B.a
C.2a D.a
答案 AC
解析 以B为坐标原点,BA,BC,BB1所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系,
则D,
B1(0,0,3a),C(0,a,0).
设点E的坐标为(a,0,z)(0≤z≤3a),
则=,
=(a,-a,z),=(a,0,z-3a).
由CE⊥平面B1DE,得CE⊥DE,CE⊥B1E,
故
即
解得z=a或z=2a,即AE=a或2a.
12.如图,在正方体ABCD-A1B1C1D1中,点P在线段B1C上运动,则( )
A.直线BD1⊥平面A1C1D
B.三棱锥P-A1C1D的体积为定值
C.异面直线AP与A1D所成的角的取值范围是
D.直线C1P与平面A1C1D所成角的正弦值的最大值为
答案 ABD
解析 对于选项A,连接B1D1(图略),由正方体可得A1C1⊥B1D1,且BB1⊥平面A1B1C1D1,
则BB1⊥A1C1,所以A1C1⊥平面BD1B1,
故A1C1⊥BD1;
同理,连接AD1,易证得A1D⊥BD1,
则BD1⊥平面A1C1D,故A正确;
对于选项B,
因为点P在线段B1C上运动,
所以=A1D·AB,面积为定值,
且C1到平面A1PD的距离即为C1到平面A1B1CD的距离,也为定值,故体积为定值,故B正确;
对于选项C,当点P与线段B1C的端点重合时,AP与A1D所成的角取得最小值为60°,故C错误;
对于选项D,因为直线BD1⊥平面A1C1D,
所以若直线C1P与平面A1C1D所成角的正弦值最大,
则直线C1P与直线BD1所成的角的余弦值最大,
则P运动到B1C中点处,即所成的角为∠C1BD1,
设棱长为1,在Rt△D1C1B中,cos∠C1BD1===,故D正确.
三、填空题(本大题共4小题,每小题5分,共20分)
13.已知点B(1,0,0),C′(1,1,1),D′(0,1,1),若点E的坐标为(-2,1,m),且点B,C′,D′,E四点共面,则实数m的值为________.
答案 1
解析 ∵B(1,0,0),C′(1,1,1),D′(0,1,1),E(-2,1,m),
∴=(0,1,1),=(-1,1,1),=(-3,1,m),
根据空间向量基本定理,存在实数x,y,
使得=x+y,
则有
解得m=1.
14.已知平面α经过点B(1,0,0),且α的法向量n=(1,1,1),则P(2,2,0)到平面α的距离为________.
答案
解析 ∵向量n=(1,1,1)为平面α的法向量,点B(1,0,0),P(2,2,0),
∴=(1,2,0),
∴P(2,2,0)到平面α的距离d===.
15.已知在正四棱台ABCD-A1B1C1D1中,上底面A1B1C1D1的边长为1,下底面ABCD的边长为2,侧棱与底面所成的角为60°,则异面直线AD1与B1C所成的角的余弦值为________.
答案
解析 设上、下底面中心分别为O1,O,则OO1⊥平面ABCD,以O为原点,直线BD,AC,OO1分别为x轴,y轴,z轴建立空间直角坐标系.
因为AB=2,A1B1=1,
所以AC=BD=2,A1C1=B1D1=.
因为平面BDD1B1⊥平面ABCD,
所以∠B1BO为侧棱与底面所成的角,故∠B1BO=60°.
设棱台高为h,则tan 60°=,h=,
所以A(0,-,0),D1,B1,
C(0,,0),
所以=,
=,
故cos〈,〉==,
故异面直线AD1与B1C所成的角的余弦值为.
16.如图,有一长方形的纸片ABCD,AB的长度为4 cm,BC的长度为3 cm,现沿它的一条对角线AC把它折叠成90°的二面角,则折叠后·=________,线段BD的长是________cm.
答案 -7
解析 如图所示,
作DE⊥AC,BF⊥AC,
垂足分别为E,F,
则AC=5,DE=BF=,
AE=CF=,EF=,
折叠后,DE,EF,FB的长度保持不变,
所以·=·(+)=·+·=5×4×+5×3×=-7,
故||2=(++)2
=||2+||2+||2+2·+2·+2·
=||2+||2+||2+0+0+0
=2+2+2=,
得BD=.
四、解答题(本大题共6小题,共70分)
17.(10分)如图所示,在四棱锥M-ABCD中,底面ABCD是边长为2的正方形,侧棱AM的长为3,且AM和AB,AD的夹角都是60°,N是CM的中点,设a=,b=,c=,试以a,b,c为基向量表示出向量,并求BN的长.
解 =+=+
=+(-)
=+[-(+)]
=-++.
所以=-a+b+c,
||2=2=2
=(a2+b2+c2-2a·b-2a·c+2b·c)=.
所以||=,即BN的长为.
18.(12分)已知空间内三点A(0,2,3),B(-2,1,6),C(1,-1,5).
(1)求以向量,为一组邻边的平行四边形的面积S;
(2)若向量a与向量,都垂直,且|a|=,求向量a的坐标.
解 (1)∵=(-2,-1,3),=(1,-3,2),
∴cos∠BAC===,
又∵∠BAC∈[0,π],
∴∠BAC=,
∴S=||||sin =7.
(2)设a=(x,y,z),
由a⊥,得-2x-y+3z=0,
由a⊥,得x-3y+2z=0,
由|a|=,得x2+y2+z2=3,
∴x=y=z=1或x=y=z=-1.
∴a=(1,1,1)或a=(-1,-1,-1).
19.(12分)如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E,F分别是AB,PB的中点.
(1)求证:EF⊥CD;
(2)在平面PAD内求一点G,使GF⊥平面PCB,并证明你的结论.
(1)证明 如图,以D为原点,分别以DA,DC,DP所在直线为x轴,y轴,z轴建立空间直角坐标系,
设AD=a,则D(0,0,0),
A(a,0,0),B(a,a,0),C(0,a,0),
E,P(0,0,a),
F.
=,=(0,a,0),
∵·=0,∴⊥,即EF⊥CD.
(2)解 设G(x,0,z),则=,
若使GF⊥平面PCB,则需·=0且·=0,
由·=·(a,0,0)
=a=0,得x=,
由·=·(0,-a,a)
=+a=0,
得z=0.
∴G点坐标为,即G为AD的中点时,GF⊥平面PCB.
20.(12分)如图所示,已知点P在正方体ABCD-A′B′C′D′的对角线BD′上,∠PDA=60°.
(1)求DP与CC′所成角的大小;
(2)求DP与平面AA′D′D所成角的大小.
解 (1)如图所示,以D为原点,DA,DC,DD′分别为x轴,y轴,z轴正方向建立空间直角坐标系,设DA=1.
则=(1,0,0),=(0,0,1).
连接BD,B′D′.
在平面BB′D′D中,延长DP交B′D′于H.
设=(m,m,1)(m>0),
由已知得〈·〉=60°,
由·=||||cos〈,〉,
可得2m=.
解得m=,
所以=.
因为cos〈,〉==,
所以〈,〉=45°,
即DP与CC′所成的角为45°.
(2)由题意得,平面AA′D′D的一个法向量是
=(0,1,0),
因为cos〈,〉
==,
所以〈,〉=60°,
可得DP与平面AA′D′D所成的角为30°.
21.(12分)如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.
(1)求证:BE⊥DC;
(2)若F为棱PC上一点,满足BF⊥AC,求二面角F-AB-P的余弦值.
(1)证明 依题意,以点A为坐标原点建立空间直角坐标系(如图),可得A(0,0,0),
B(1,0,0),C(2,2,0),D(0,2,0),
P(0,0,2).
由E为棱PC的中点,得E(1,1,1),
所以=(0,1,1),=(2,0,0),
故·=0,
所以BE⊥DC.
(2)解 =(1,2,0),=(-2,-2,2),=(2,2,0),=(1,0,0).
由点F在棱PC上,设=λ(0≤λ≤1),
故=+=+λ=(1-2λ,2-2λ,2λ).
由BF⊥AC,得·=0,
则2(1-2λ)+2(2-2λ)=0,解得λ=,
即=.
设n1=(x,y,z)为平面FAB的法向量,
则
即
不妨令z=1,可得n1=(0,-3,1)为平面FAB的一个法向量.
易知向量n2=(0,1,0)为平面ABP的一个法向量,
则cos〈n1,n2〉===-.
由图可知,二面角F-AB-P为锐角,
所以二面角F-AB-P的余弦值为.
22.(12分)如图所示,在等腰梯形ABCD中,AB∥CD,AD=AB=BC=2,CD=4,E为CD的中点,AE与BD交于点O,将△ADE沿AE折起,使点D到达点P的位置(P 平面ABCE).
(1)证明:平面POB⊥平面ABCE;
(2)若PB=,试判断线段PB上是否存在一点Q(不含端点),使得直线PC与平面AEQ所成角的正弦值为,若存在,求出的值;若不存在,说明理由.
(1)证明 在梯形ABCD中,连接BE(图略),
∵AD=AB=BC=2,CD=4,E为中点,
∴四边形ABED为菱形,∴BD⊥AE,
∴OB⊥AE,OD⊥AE,
即OB⊥AE,OP⊥AE,且OB∩OP=O,
OB 平面POB,OP 平面POB,
∴AE⊥平面POB.
又AE 平面ABCE,∴平面POB⊥平面ABCE.
(2)由(1)可知四边形ABED为菱形,
∴AD=DE=2,
在等腰梯形ABCD中,AE=BC=2,
∴△PAE为正三角形,∴OP=,同理OB=,
∵PB=,∴OP2+OB2=PB2,∴OP⊥OB.
由(1)可知OP⊥AE,OB⊥AE,
以O为原点,,,分别为x轴,y轴,z轴,建立空间直角坐标系O-xyz,
则P(0,0,),A(-1,0,0),B(0,,0),C(2,,0),
E(1,0,0),
∴=(1,0,),=(0,,-),
=(2,,-),=(2,0,0),
设=λ(0<λ<1),
=+=+λ=(1,λ,-λ),
设平面AEQ的一个法向量为n=(x,y,z),
则即
取x=0,y=1,得z=,
∴n=,
设直线PC与平面AEQ所成角为θ,θ∈,
则sin θ=|cos〈,n〉|==,
即=,
化简得4λ2-4λ+1=0,解得λ=,
∴存在点Q为PB的中点时,使直线PC与平面AEQ所成角的正弦值为.
